Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

•

On a graph, vertical boundary lines can be used to identify the domain, or the set of “allowable inputs” for a

function.

•

On a graph, horizontal boundary lines can be used to identify the range, or the set of y-values (outputs) generated

by the function.

•

When a function is stated as an equation, the implied domain is the set of x-values that yield real number outputs.

•

x-values that cause a denominator of zero or that cause the radicand of a square root expression to be negative

must be excluded from the domain.

•

The phrase “y is a function of x,” is written as . This notation enables us to summarize the three most

important aspects of a function with a single expression (input, sequence of operations, output).

EXERCISES

16. State the implied domain of each function:

a. b.

17. Determine , and h(3a) for

18. Determine if the mapping given represents a function. If not, explain how the deﬁnition of a function is violated.

19. For the graph of each function shown, (a) state the domain and range, (b) ﬁnd the value of f(2), and (c) determine

the value(s) of x for which .

I. II. III.

SECTION 1.4 Linear Functions, Special Forms, and More on Rates of Change

KEY CONCEPTS

•

The equation of a nonvertical line in slope-intercept form is or . The slope of the line

is m and the y-intercept is (0, b).

•

To graph a line given its equation in slope-intercept form, plot the y-intercept, then use the slope ratio to

ﬁnd a second point, and draw a line through these points.

•

If the slope m and a point (x

, y

) on the line are known, the equation of the line can be written in point-slope

form: .y ⫺ y

⫽ m1x ⫺ x

m ⫽

¢y

¢x

1x2⫽ mx ⫹ by ⫽ mx ⫹ b

5⫺5

⫺5

5⫺5

⫺5

5⫺5

⫺5

f 1x2⫽ 1

Apollo

Jupiter

Ares

Neptune

Mercury

Venus

Ceres

Mars

messenger

war

craftsman

love and beauty

music and healing

oceans

all things

agriculture

Mythological

deities

Primary

concern

h1x2⫽ 2x

⫺ 3x.h1⫺22, h1⫺

g1x2⫽

x ⫺ 4

⫺ x ⫺ 6

1x2⫽ 24x ⫹ 5

y ⫽ f 1x2

180 CHAPTER 1 Relations, Functions, and Graphs 1–96

College Algebra G&M—

cob19545_ch01_178-186.qxd 11/25/10 7:52 PM Page 180

•

A secant line is the straight line drawn through two points on a nonlinear graph.

•

The notation literally means the quantity measured along the y-axis is changing with respect to changes

in the quantity measured along the x-axis.

EXERCISES

20. Write each equation in slope-intercept form, then identify the slope and y-intercept.

a. b.

21. Graph each equation using the slope and y-intercept.

a. b.

22. Graph the line with the given slope through the given point.

a. b.

23. What are the equations of the horizontal line and the vertical line passing through

Which line is the point (7, 5) on?

24. Find the equation of the line passing through (1, 2) and Write your ﬁnal

answer in slope-intercept form.

25. Find the equation for the line that is parallel to and passes through

the point (3, 4). Write your ﬁnal answer in slope-intercept form.

26. Determine the slope and y-intercept of the line shown. Then write the equation of

the line in slope-intercept form and interpret the slope ratio in the context

of this exercise.

27. For the graph given, (a) ﬁnd the equation of the line in point-slope form, (b) use the

equation to predict the x- and y-intercepts, (c) write the equation in slope-intercept

form, and (d) ﬁnd y when , and the value of x for which

SECTION 1.5 Solving Equations and Inequalities Graphically;

Formulas and Problem Solving

KEY CONCEPTS

•

To use the intersection-of-graphs method for solving equations, assign the left-hand expression as Y

and the

right-hand as Y

. The solution(s) of the original equation are the x-coordinate(s) of the point(s) of intersection of

the graphs of Y

and Y

•

When an equation is written in the form , the solutions can be found using the x-Intercept/Zeroes method.

Assign h(x) as Y

, and ﬁnd the x-intercepts of its graph.

•

Linear inequalities can be solved by ﬁrst applying the intersection-of-graphs method to identify the boundary

value of the solution interval. Next, the solution is determined by a careful observation of the relative positions of

the graphs (is Y

above or below Y

) and the given inequality.

•

To solve formulas for a speciﬁed variable, focus on the object variable and apply properties of equality to write

this variable in terms of all others.

•

The basic elements of good problem solving include:

1. Gathering and organizing information

2. Making the problem visual

3. Developing an equation model

4. Using the model to solve the application

For a complete review, see the problem-solving guide on page 157.

h1x2⫽ 0

y ⫽ 15.x ⫽ 20

m ⫽

¢W

¢R

4x ⫺ 3y ⫽ 12

1⫺3, 52.

1⫺2, 52?

m ⫽⫺

; 1⫺2, 32m ⫽

; 11, 42

h1x2⫽

x ⫺ 3f 1x2⫽⫺

x ⫹ 1

5x ⫺ 3y ⫽ 154x ⫹ 3y ⫺ 12 ⫽ 0

m ⫽

¢y

¢x

1–97 Summary and Concept Review 181

College Algebra G&M—

10862

Wolf population (100s)

Rabbit population (100s)

Exercise 26

108620

100

Exercise 27

cob19545_ch01_178-186.qxd 1/7/11 5:33 PM Page 181

EXERCISES

28. Solve the following equation using the intersection-of-graphs method.

29. Solve the following equation using the x-intercept/zeroes method.

30. Solve the following inequality using the intersection-of-graphs method.

Solve for the speciﬁed variable in each formula or literal equation.

31. for h 32.

33. for x 34. for y

Use the problem-solving guidelines (page 157) to solve the following applications.

35. At a large family reunion, two kegs of lemonade are available. One is 2% sugar (too sour) and the second is 7% sugar

(too sweet). How many gallons of the 2% keg, must be mixed with 12 gallons of the 7% keg to get a 5% mix?

36. A rectangular window with a width of 3 ft and a height of 4 ft is topped by a semi-circular window. Find the total

area of the window.

37. Two cyclists start from the same location and ride in opposite directions, one riding at 15 mph and the other at 18 mph.

If their radio phones have a range of 22 mi, how many minutes will they be able to communicate?

SECTION 1.6 Linear Function Models and Real Data

KEY CONCEPTS

•

A scatterplot is the graph of all the ordered pairs in a real data set.

•

When drawing a scatterplot, be sure to scale the axes to comfortably ﬁt the data.

•

If larger inputs tend to produce larger output values, we say there is a positive association.

•

If larger inputs tend to produce smaller output values, we say there is a negative association.

•

If the data seem to cluster around an imaginary line, we say there is a linear association between the variables.

•

If the data clearly cannot be approximated by a straight line, we say the variables exhibit a nonlinear association

(or sometimes no association).

•

The correlation coefﬁcient r measures how tightly a set of data points cluster about an imaginary curve. The

strength of the correlation is given as a value between ⫺1 and 1. Measures close to ⫺1 or 1 indicate a very strong

correlation. Measures close to 0 indicate a very weak correlation.

•

We can attempt to model linear data sets using an estimated line of best ﬁt.

•

A regression line minimizes the vertical distance between all data points and the graph itself, making it the unique

line of best ﬁt.

EXERCISES

38. To determine the value of doing homework, a student in college algebra collects data

on the time spent by classmates on their homework in preparation for a quiz. Her data

is entered in the table shown. (a) Use a graphing calculator to draw a scatterplot of

the data. (b) Does the association appear linear or nonlinear? (c) Is the association

positive or negative?

39. If the association in Exercise 38 is linear, (a) use a graphing calculator to ﬁnd a linear

function that models the relation (study time, grade), then (b) graph the data and the line

on the same screen. (c) Does the correlation appear weak or strong?

40. According to the function model from Exercise 39, what grade can I expect if I study

for 120 minutes?

2x ⫺ 3y ⫽ 6ax ⫹ b ⫽ c

P ⫽ 2L ⫹ 2W for LV ⫽ ␲r

31x ⫹ 22⫺ 2.2 6 ⫺2 ⫹ 410.2 ⫺ 0.5x2

21x ⫺ 12⫹

⫽ 51

x ⫹

2⫺

31x ⫺ 22⫹ 10 ⫽ 16 ⫺ 213 ⫺ 2x2

182 CHAPTER 1 Relations, Functions, and Graphs 1–98

College Algebra G&M—

Exercise 38

(min study) (quiz score)

45 70

30 63

10 59

20 67

60 73

70 85

90 82

75 90

cob19545_ch01_178-186.qxd 1/7/11 4:41 PM Page 182

1–99 Practice Test 183

College Algebra G&M—

PRACTICE TEST

1. Solve each equation.

c. ; for C

d. ; for W

. How much water that is must be mixed

with 25 gal of water at , so that the resulting

temperature of the water will be .

3. To make the bowling team, Jacques needs a three-

game average of 160. If he bowled 141 and 162 for the

ﬁrst two games, what score S must be obtained in the

third game so that his average is at least 160?

4. In the 2009 movie Star Trek (Chris Pine, Zachary

Quinto, Zoy Zaldana, Eric Bana), Sulu falls off of

the drill platform without a parachute, and Kirk

dives off the platform to save him. To slow his fall,

Zulu uses a spread-eagle tactic, while Kirk keeps his

body straight and arms at his side, to maximize his

falling speed. If Sulu is falling at a rate of 180 ft/sec,

while Kirk is falling at 250 ft/sec, how long would it

take Kirk to reach Sulu, if it took Kirk a full 2 sec to

react and dive after Sulu?

5. Two relations here are functions and two are not.

Identify the nonfunctions (justify your response).

a. b.

c. d.

6. Determine whether the lines are parallel,

perpendicular, or neither:

and .

7. Graph the line using the slope and y-intercept:

8. Find the center and radius of the circle deﬁned by

, then sketch its graph.

9. After 2 sec, a car is traveling 20 mph. After 5 sec, its

speed is 40 mph. Assuming the relationship is linear,

ﬁnd the velocity equation and use it to determine the

speed of the car after 9 sec.

10. Find the equation of the line parallel to

containing the point . Answer in slope-

intercept form.

12, ⫺22

6x ⫹ 5y ⫽ 3,

⫹ y

⫺ 4x ⫹ 6y ⫺ 3 ⫽ 0

x ⫹ 4y ⫽ 8

: y ⫽

x ⫹ 7L

: 2x ⫹ 5y ⫽⫺15

y ⫽ x

⫹ 2x

冟

⫹ 1 ⫽ x

y ⫽ 25 ⫺ 2x

x ⫽ y

⫹ 2y

97°F

91°F

102°F

P ⫽ 2L ⫹ 2W

P ⫽ C ⫹ k

⫺5.7 ⫹ 3.1x ⫽ 14.5 ⫺ 41x ⫹ 1.52

⫺

x ⫺ 5 ⫽ 7 ⫺ 1x ⫹ 32

11. My partner and I are at coordinates on a

map. If our destination is at coordinates ,

(a) what are the coordinates of the rest station

located halfway to our destination? (b) How far

away is our destination? Assume that each unit is

1 mi.

12. Write the equations for lines L

and L

shown.

13. State the domain and range for the relations shown

on graphs 13(a) and 13(b).

Exercise 13(a) Exercise 13(b)

14. For the linear function shown,

a. Determine the value of

W(24) from the graph.

b. What input h will give an

output of

c. Find a linear function for

the graph.

d. What does the slope indicate in this context?

e. State the domain and range of h.

15. Given :

a. b. f

1a ⫹ 32f 1

1x2⫽

2 ⫺ x

, evaluate and simplify

W1h2⫽ 375?

6⫺4

⫺5

6⫺4

⫺5

5⫺5

⫺5

135, ⫺122

1⫺20, 152

4080162432

500

300

400

200

100

Hours worked

Wages earned

W(h)

cob19545_ch01_178-186.qxd 11/1/10 2:33 PM Page 183

16. In 2007, there were 3.3 million

Apple iPhones sold worldwide.

By 2009, this ﬁgure had

jumped to approximately

30.3 million [Source:

http://brainstormtech.blogs.

fortune.cnn.com/2009/03/12/].

Assume that for a time, this

growth could be modeled by a

linear function. (a) Determine

the rate of change , and

(b) interpret it in this context. Then use the rate of

change to (c) approximate the number of sales in

2008, and what the projected sales would be for

2010 and 2011.

17. Solve the following equations using the

x-intercept/zeroes method.

18. Solve the following inequalities using the

intersection-of-graphs method.

210.75x ⫺ 126 0.7 ⫹ 0.513x ⫺ 12

3x ⫺ 15 ⫺ x2ⱖ 215 ⫺ x2⫹ 3

210.7x ⫺ 1.32⫹ 2.6 ⫽ 2x ⫺ 310.2x ⫺ 22

2x ⫹ a4 ⫺

xb⫽⫺120 ⫹ x2

¢sales

¢time

184 CHAPTER 1 Relations, Functions, and Graphs 1–100

College Algebra G&M—

19. To study how annual

rainfall affects the ability

to attain certain levels of

livestock production, a

local university collects

data on the average

annual rainfall for a

particular area and

compares this to the

average number of

free-ranging cattle per

acre for ranchers in that

area. The data collected

are shown in the table. (a) Use a graphing calculator

to draw a scatterplot of the data. (b) Does the

association appear linear or nonlinear? (c) Is the

association positive or negative?

20. If the association in Exercise 19 is linear, (a) use a

graphing calculator to ﬁnd a linear function that

models the relation (rainfall, cattle per acre), (b) use

the function to ﬁnd the number of cattle per acre that

might be possible for an area receiving 50 in. of

rainfall per year, and (c) state whether the correlation

is weak or strong.

STRENGTHENING CORE SKILLS

The Various Forms of a Linear Equation

Learning mathematics is very much like the construction of a skyscraper. The ﬁnal height of the skyscraper ultimately

depends on the strength of the foundation and quality of the frame supporting each new ﬂoor as it is built. Our

previous work with linear functions and their graphs, while having a number of useful applications, is actually the

foundation on which much of our future work is built. For this reason, it’s important you gain a certain ﬂuency with

linear functions and relationships—even to a point where things come to you effortlessly and automatically. As

noted mathematician Henri Lebesque once said, “An idea reaches its maximum level of usefulness only when you

understand it so well that it seems like you have always known it. You then become incapable of seeing the idea as

anything but a trivial and immediate result.” These formulas and concepts, while simple, have an endless number of

signiﬁcant and substantial applications.

Forms and Formulas

slope formula point-slope form slope-intercept form standard form

given any two points given slope m and given slope m and A, B, and C are integers

on the line any point y-intercept (0, b) (used in linear systems)1x

, y

Ax ⫹ By ⫽ Cy ⫽ mx ⫹ by ⫺ y

⫽ m1x ⫺ x

2m ⫽

⫺ y

⫺ x

Exercise 19

Rainfall Cattle

(in.) per Acre

12 2

16 3

19 7

23 9

28 11

32 22

37 23

40 26

Exercise 16

cob19545_ch01_178-186.qxd 11/1/10 2:33 PM Page 184

Characteristics of Lines

increasing decreasing

(0, y)(x, 0)

let , let , line slants upward line slants downward

solve for y solve for x from left to right form left to right

Relationships between Lines

intersecting parallel perpendicular dependent

lines intersect lines do not lines intersect lines intersect

at one point intersect at right angles at all points

Special Lines

horizontal vertical identity

horizontal line vertical line the input value

through k through h identiﬁes the output

Use the formulas and concepts reviewed here to complete the following exercises.

For the two points given: (a) compute the slope of the line through the points and state whether the line is increasing

or decreasing, (b) ﬁnd the equation of the line in point-slope form, then write the equation in slope-intercept form, and

Exercise 1: P

(0, 5) P

(6, 7) Exercise 4: P

(3, 2)

Exercise 2: P

(3, 2) P

(0, 9) Exercise 5:

Exercise 3: P

(3, 2) P

(9, 5) Exercise 6: P

1⫺8, ⫺22P

12, ⫺72

16, ⫺12P

1⫺2, 52

1⫺5, ⫺42

y-x-

y ⫽ xx ⫽ hy ⫽ k

⫽ b

⫽ m

⫽⫺1 m

⫽ m

y ⫽ 0x ⫽ 0

m 6 0m 7 0

x-intercepty-intercept

Evaluating Expressions and Looking for Patterns

These “explorations” are designed to explore the full potential of a graphing calculator, as well as to use this potential

to investigate patterns and discover connections that might otherwise be overlooked. In this exploration and discovery,

we point out the various ways an expression can be evaluated on a graphing calculator. Some ways seem easier, faster,

and/or better than others, but each has advantages and disadvantages depending on the task at hand, and it will help to

be aware of them all for future use.

One way to evaluate an expression is to use the TABLE feature of a graphing calculator, with the expression

entered as Y

on the screen. If you want the calculator to generate inputs, use the (TBLSET) screen

to indicate a starting value (TblStartⴝ) and an increment value ( ), and set the calculator in Indpnt:

mode (to input speciﬁc values, the calculator should be in Indpnt: AUTO

mode). After pressing (TABLE), the calculator shows the corresponding

input and output values.

Expressions can also be evaluated on the home screen for a single value or a series

of values. Enter the expression on the screen (see Figure 1.105) and

use (QUIT) to get back to the home screen. To evaluate this expression,

access Y

using (Y-VARS), and use the ﬁrst option 1:Function . This

brings us to a submenu where any of the equations Y

through Y

(actually Y

) can

be accessed. Since the default setting is the one we need (1:Y1), simply press and

appears on the home screen. To evaluate a single input, simply enclose it in

ENTER

VARS

MODE

2nd

⫺

x ⫹ 5

GRAPH

2nd

ASKASK

AUTO

⌬Tbl ⴝ

WINDOW

2nd

1–101 Calculator Exploration and Discovery 185

College Algebra G&M—

CALCULATOR EXPLORATION AND DISCOVERY

Figure 1.105

cob19545_ch01_178-186.qxd 11/1/10 2:33 PM Page 185

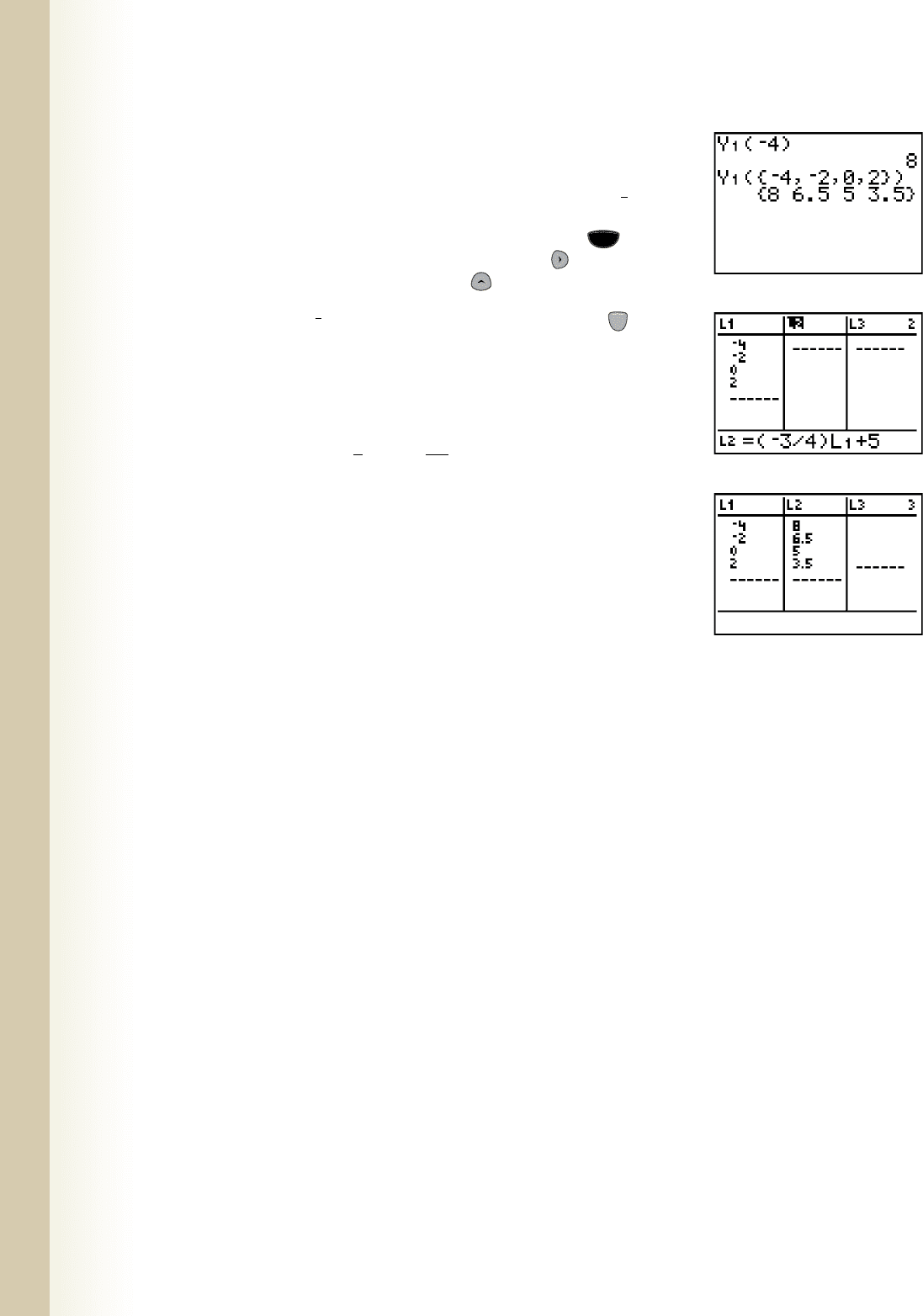
parentheses. To evaluate more than one input, enter the numbers as a set of values with

the set enclosed in parentheses. In Figure 1.106, Y

has been evaluated for ,

then simultaneously for , and 2.

A third way to evaluate expressions is using a list, with the desired inputs entered

in List 1 (L1), then List 2 (L2) deﬁned in terms of L1. For example,

will return the same values for inputs of and 2 seen previously on the home

screen (remember to clear the lists ﬁrst). Lists are accessed by pressing 1:Edit.

Enter the numbers , and 2 in L1, then use the right arrow to move to L2. It

is important to note that you next press the up arrow key so that the cursor overlies

L2. The bottom of the screen now reads “ ” and the calculator is waiting for us to

deﬁne L2. After entering (see Figure 1.107) and pressing we

obtain the same outputs as before (see Figure 1.108). The advantage of using the “list”

method is that we can further explore or experiment with the output values in a search

for patterns.

Exercise 1: Evaluate the expression on the list screen, using consecutive

integer inputs from to 6 inclusive. What do you notice about the outputs?

Exercise 2: Evaluate the expression on the list screen, using

consecutive integer inputs from to 6 inclusive. We suspect there is a pattern to the

output values, but this time the pattern is very difﬁcult to see. On the home screen,

compute the difference between a few successive outputs from L2 [for example,

)]. What do you notice?

L2112⫺ L212

⫺6

L1 ⫺ 19.1

⫺6

0.2L1 ⫹ 3

ENTER

L2 ⫽⫺

L1 ⫹ 5

L2 ⫽

⫺4, ⫺2, 0

STAT

⫺4, ⫺2, 0,

L2 ⫽⫺

L1 ⫹ 5

⫺2, 0,x ⫽⫺4

x ⫽⫺4

186 CHAPTER 1 Relations, Functions, and Graphs 1–102

College Algebra G&M—

Figure 1.106

Figure 1.107

Figure 1.108

cob19545_ch01_178-186.qxd 11/1/10 2:34 PM Page 186

College Algebra Graphs & Models—

More on the Domain 230

2.5 Piecewise-Deﬁned Functions 245

2.6 Variation: The Toolbox Functions in Action 259

CHAPTER CONNECTIONS

Viewing a function in terms of an equation, a

table of values, and the related graph, often

brings a clearer understanding of the

relationships involved. For example, the power

generated by a wind turbine is often modeled

by the function , where P is the

power in watts and v is the wind velocity in

miles per hour. While the formula enables us

to predict the power generated for a given wind

speed, the graph offers a visual representation

of this relationship, where we note a rapid

growth in power output as the wind speed

increases. This application appears as

Exercise 107 in Section 2.2.

Check out these other real-world connections:

䊳

Analyzing the Path of a Projectile

(Section 2.1, Exercise 57)

䊳

Altitude of the Jet Stream

(Section 2.3, Exercise 61)

䊳

Amusement Arcades

(Section 2.5, Exercise 42)

䊳

Volume of Phone Calls

(Section 2.6, Exercise 55)

P 1v2

125

187

cob19545_ch02_187-201.qxd 11/23/10 8:09 AM Page 187

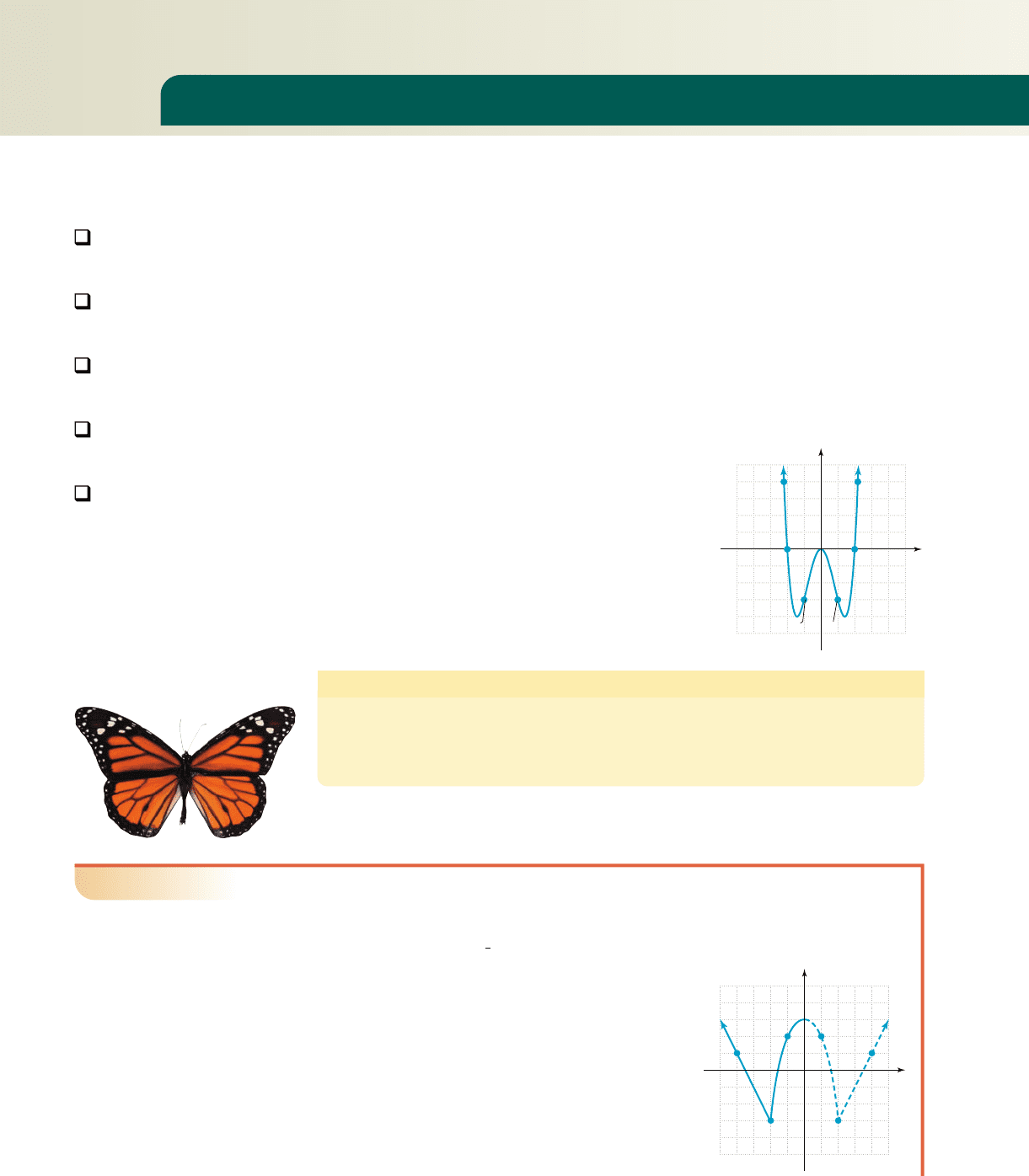
2.1 Analyzing the Graph of a Function

In this section, we’ll consolidate and reﬁne many of the ideas we’ve encountered

related to functions. When functions and graphs are applied as real-world models, we

create numeric and visual representations that enable an informed response to ques-

tions involving maximum efﬁciency, positive returns, increasing costs, and other rela-

tionships that can have a great impact on our lives.

A. Graphs and Symmetry

While the domain and range of a function will remain dominant themes in our study,

for the moment we turn our attention to other characteristics of a function’s graph.

We begin with the concept of symmetry.

Symmetry with Respect to the y-Axis

Consider the graph of shown in Fig-

ure 2.1, where the portion of the graph to the left of the

y-axis appears to be a mirror image of the portion to the

right. A function is symmetric to the y-axis if, given

any point (x, y) on the graph, the point is also

on the graph. We note that is on the graph, as

is and that is an x-intercept of the

graph, as is (2, 0). Functions that are symmetric with

respect to the y-axis are also known as even functions

and in general we have:

Even Functions: y-Axis Symmetry

A function f is an even function if and only if, for each point (x, y) on the graph of f,

the point ( , y) is also on the graph. In function notation

Symmetry can be a great help in graphing new functions, enabling us to plot fewer

points and to complete the graph using properties of symmetry.

EXAMPLE 1

䊳

Graphing an Even Function Using Symmetry

a. The function g(x) in Figure 2.2 (shown in solid blue) is known to be even.

Draw the complete graph.

b. Show that is an even function using

the arbitrary value [show ],

then sketch the complete graph using h(0),

h(1), h(8), and y-axis symmetry.

Solution

䊳

a. To complete the graph of g (see Figure 2.2)

use the points ( , 1), ( ), ( , 2),

and y-axis symmetry to ﬁnd additional points.

The corresponding ordered pairs are (4, 1),

(2, ), and (1, 2), which we use to help

draw a “mirror image” of the partial graph

given.

3

12, 34

h1k2 h1k2x  k

h1x2 x

f 1x2 f 1x2

x

12, 0211, 32,

11, 32

1x, y2

1x2 x

 4x

188 2–2

College Algebra Graphs & Models—

LEARNING OBJECTIVES

In Section 2.1 you will see

how we can

A. Determine whether a

function is even, odd, or

neither

B. Determine intervals

where a function is

positive or negative

C. Determine where a

function is increasing or

decreasing

D. Identify the maximum and

minimum values of a

function

E. Locate local maximum

and minimum values

using a graphing

calculator

(1, 3)

(2, 0)

(2.2, ~4)

(1, 3)

55

5

f(x)  x

 4x

(2, 0)

(2.2, ~4)

55

5

g(x)

(4, 1)

(1, 2)

(1, 2)

(4, 1)

(2, 3) (2, 3)

Figure 2.2

Figure 2.1

cob19545_ch02_187-201.qxd 11/1/10 7:35 AM Page 188

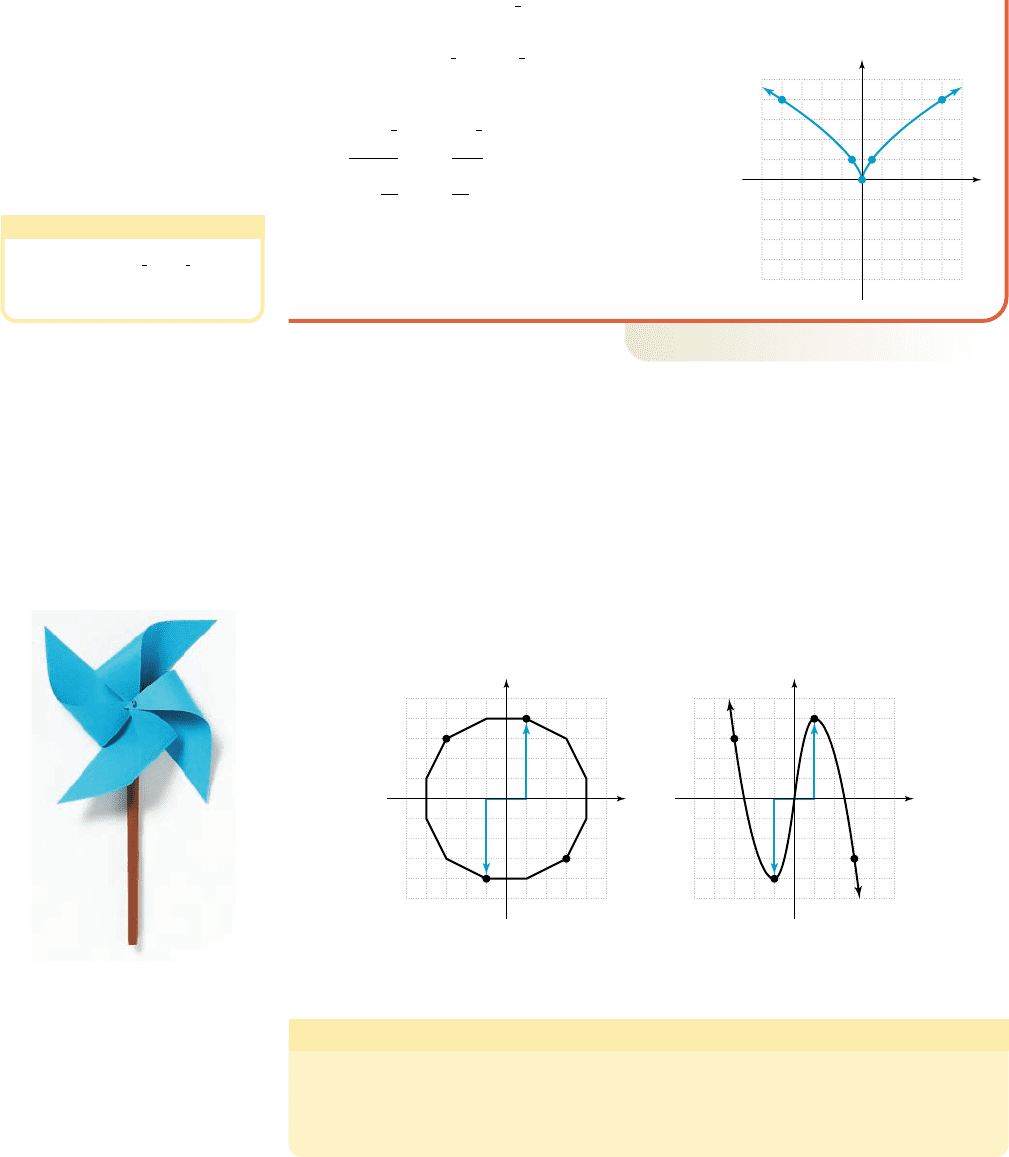
b. To prove that is an even function, we

must show for any constant k.

After writing as , we have:

ﬁrst step of proof

evaluate

(

) and

(

)

radical form

✓ result:

Using , , and with

y-axis symmetry produces the graph shown in

Figure 2.3.

Now try Exercises 7 through 12

䊳

Symmetry with Respect to the Origin

Another common form of symmetry is known as symmetry to the origin.As the name

implies, the graph is somehow “centered” at (0, 0). This form of symmetry is easy to

see for closed ﬁgures with their center at (0, 0), like certain polygons, circles, and

ellipses (these will exhibit both y-axis symmetry and symmetry with respect to the

origin). Note the relation graphed in Figure 2.4 contains the points ( , 3) and (3, ),

along with ( ) and (1, 4). But the function f(x) in Figure 2.5 also contains these

points and is, in the same sense, symmetric to the origin (the paired points are on op-

posite sides of the x- and y-axes, and a like distance from the origin).

1, 4

33

h182 4h112 1h102 0

1k2

 k

 2

1k2

ⱨ 2

1k2

31k2

ⱨ 31k2

h1k2ⱨ h1k2

h1k2 h1k2

h1x2 x

Functions symmetric to the origin are known as odd functions and in general

we have:

Odd Functions: Symmetry About the Origin

A function f is an odd function if and only if, for each point (x, y) on the graph of f,

the point ( ) is also on the graph. In function notation

1x2f 1x2

x, y

2–3 Section 2.1 Analyzing the Graph of a Function 189

College Algebra Graphs & Models—

1010

5

h(x)

(8, 4)

(1, 1)

(0, 0)

(8, 4)

(1, 1)

Figure 2.3

WORTHY OF NOTE

The proof can also be demon-

strated by writing as , and

you are asked to complete this

proof in Exercise 69.

55

5

(3, 3)

(1, 4)

(1, 4)

(3, 3)

55

5

(3, 3)

(1, 4)

(1, 4)

f(x)

(3, 3)

Figure 2.4 Figure 2.5

cob19545_ch02_187-201.qxd 11/1/10 7:35 AM Page 189