Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


560 CHAPTER 5 An Introduction to Trigonometric Functions 5-58
Solution
a. Since , the correct match is (IV).
b. Since , the correct match is (II).
c. Since , the correct match is (I).
d. Since , the correct match is (V).
e. Since , the correct match is (III).
Now try Exercises 9 and 10
Many of the transformations applied to algebraic graphs can also be applied to
trigonometric graphs. These transformations may stretch, reflect, or translate the graph,
but it will still retain its basic shape. In numerous applications it will help if you’re
able to draw a quick, accurate sketch of the transformations involving To
assist this effort, we’ll begin with the interval combine the characteristics just
listed with some simple geometry, and offer the following four-step process. Steps I
through IV are illustrated in Figures 5.57 through 5.60.
Step I: Draw the y-axis, mark zero halfway up, with and 1 an equal distance
from this zero. Then draw an extended t-axis and tick mark to the
extreme right (Figure 5.57).
Step II: On the t-axis, mark halfway between 0 and and label it “ ” mark
halfway between on either side and label the marks and Halfway
between these you can draw additional tick marks to represent the remain-
ing multiples of (Figure 5.58).
Step III: Next, lightly draw a rectangular frame, which we’ll call the reference
rectangle, units wide and 2 units tall, centered on the t-axis and
with the y-axis along one side (Figure 5.59).
Step IV: Knowing is positive and increasing in QI, that the range is
that the zeroes are 0, and and that maximum and minimum values
occur halfway between the zeroes (since there is no horizontal shift), we can
draw a reliable graph of by partitioning the rectangle into four
equal parts to locate these values (note bold tick-marks). We will call this
partitioning of the reference rectangle the rule of fourths, since we are then
scaling the t-axis in increments of (Figure 5.60).
P
4
y sin t
2,,
31, 14,y sin t
P 2
4
3
2
.
2
,2
2
1
30, 24,
f 1t2 sin t.
sin a
11
2
b sin a
3
2
4b sin a
3
2
b
sin 1212 sin1 202 sin
sin
a
17
2
b sina
2
8b sin
2
sin
a
6
bsin
6
sin
a
4
8b sin
4
Figure 5.57
Figure 5.58 Figure 5.59 Figure 5.60
t
y
1
1
0
2
t
y
1
1
0
3
2
2
2
t
y
1
1
0
3
2
2
2
Increasing Decreasing
t
y
1
1
0
3
2
2
2
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 560 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
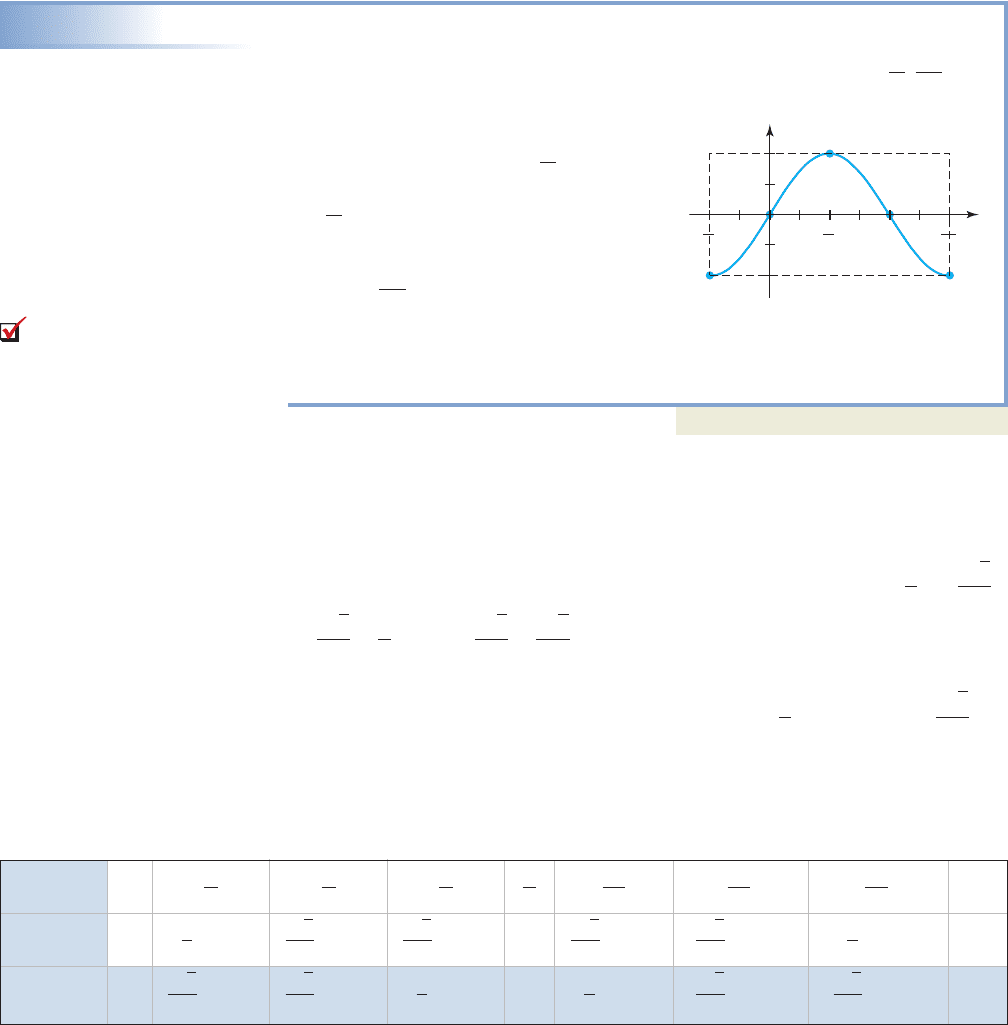
5-59 Section 5.5 Graphs of the Sine and Cosine Functions; Cosecant and Secant Functions 561
EXAMPLE 3
Graphing Using a Reference Rectangle
Use steps I through IV to draw a sketch of for the interval
Solution
Start by completing steps I and II, then
extend the t-axis to include Beginning
at draw a reference rectangle units
wide and 2 units tall, centered on the x-axis
. After applying the rule of
fourths, we note the zeroes occur at and with the max/min values
spaced equally between and on either side. Plot these points and connect them with
a smooth curve (see the figure).
Now try Exercises 11 and 12
B. Graphing f(t)
With the graph of established, sketching the graph of is a very
natural next step. First, note that when so the graph of
will begin at (0, 1) in the interval Second, we’ve seen
and are all points on the unit circle since they satisfy
Since and the equation can be
obtained by direct substitution. This means if then and
vice versa, with the signs taken from the appropriate quadrant. The table of values
for cosine then becomes a simple variation of the table for sine, as shown in Table 5.8
for
The same values can be taken from the unit circle, but this view requires much
less effort and easily extends to values of t in Using the points from
Table 5.8 and its extension through , we can draw the graph of in
and identify where the function is increasing and decreasing in this interval.
See Figure 5.61.
30, 24
y cos t3, 24
3, 24.
t 30, 4.
cos t
13
2
sin t
1
2
,
cos
2
t sin
2
t 1sin t y,cos t xx
2
y
2
1.
a
12
2
,
12
2
ba
13
2
,
1
2
b
a
1
2
,
13
2
b,30, 24.
y cos tt 0, cos t 1
f 1t2 cos tf1t2 sin t
cos t
t ,t 0
aending at
3
2
b
2
2
,
2
.
Increasing Decreasing
t
y
1
1
3
2
2
2
c
2
,
3
2
d.y sin t
y sin t
A. You’ve just learned
how to graph using
special values and symmetry
f1t2 sin t
Table 5.8
t 0
sin t 01 0
cos t 10 1
13
2
0.87
12
2
0.71
1
2
0.5
1
2
0.5
12
2
0.71
13
2
0.87
1
2
0.5
12
2
0.71
13
2
0.87
13
2
0.87
12
2
0.71
1
2
0.5
5
6
3
4
2
3
2
3
4
6
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 561 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
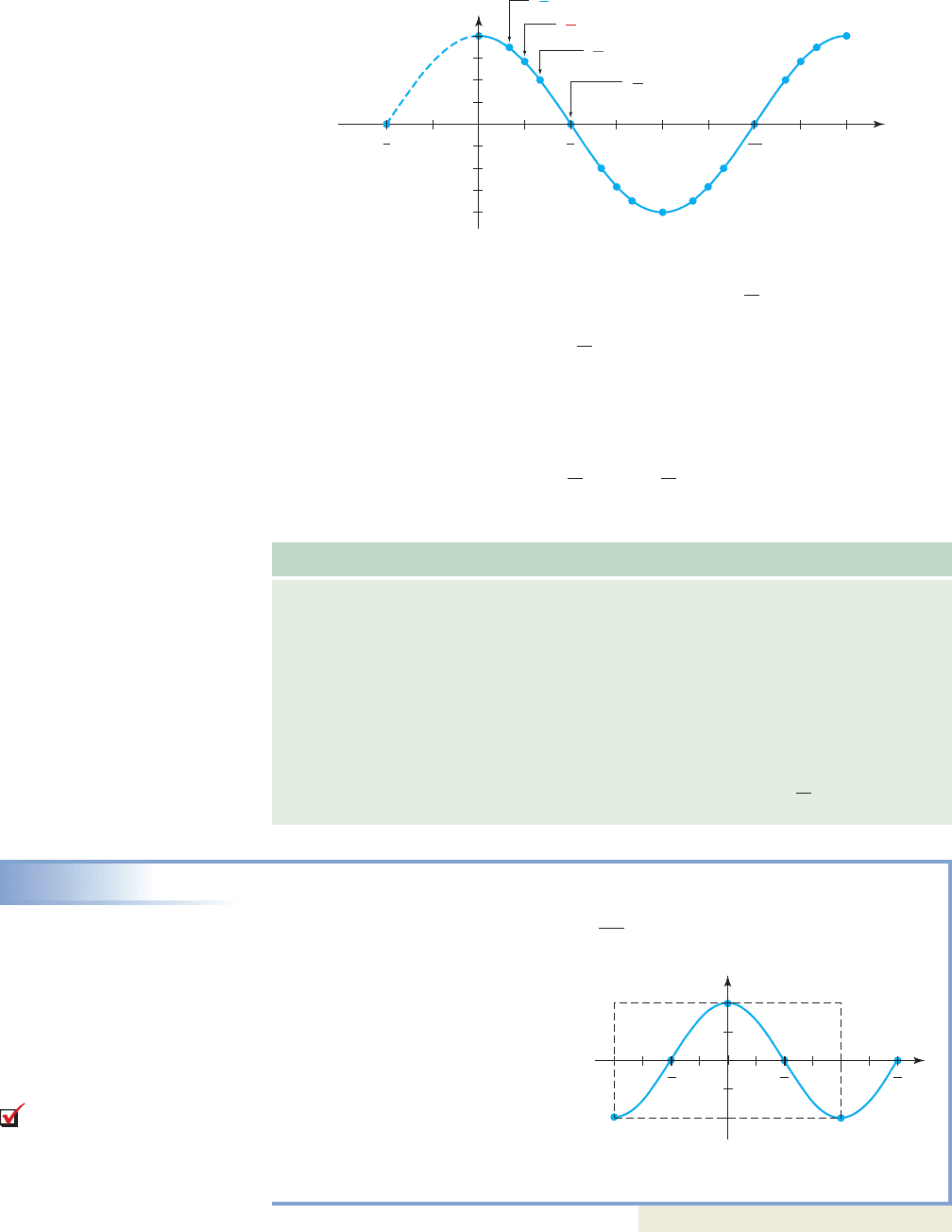
562 CHAPTER 5 An Introduction to Trigonometric Functions 5-60
The function is decreasing for and increasing for The end
result appears to be the graph of shifted to the left units, a fact more easily
seen if we extend the graph to as shown. This is in fact the case, and
is a relationship we will later prove in Chapter 6. Like the function
is periodic with period with the graph extending infinitely in both directions.
Finally, we note that cosine is an even function, meaning for all
t in the domain. For instance, (see Figure 5.61). Here is a
summary of important characteristics of the cosine function.
Characteristics of f(t) cos t
For all real numbers t and integers k,
Domain Range Period
Symmetry Maximum value Minimum value
even
Increasing Decreasing Zeroes
EXAMPLE 4
Graphing Using a Reference Rectangle
Draw a sketch of for
Solution
After completing steps I and II,
extend the negative x-axis to include
Beginning at draw a
reference rectangle units wide
and 2 units tall, centered on the
x-axis. After applying the rule of
fourths, we note the zeroes will
occur at with
the max/min values spaced equally between these zeroes and on either side
Finally, we extend the graph to include
Now try Exercises 13 and 14
3/2.1at t , t 0, and t 2.
t /2 and t /2,
2
,.
t in c,
3
2
d.y cos t
y cos t
t
2
k10, 21, 22
at t 2kat t 2kcos1t2 cos t
cos t 1cos t 1
231, 141q, q2
cos
a
2
b cos a
2
b 0
cos1t2 cos t
P 2,
y cos ty sin t,
2
2
y sin t
t in 1, 22.t in 10, 2,
D
e
c
r
e
a
si
n
g
I
n
c
reas
i
n
g
cos t
1
0
2
2
3
2
t
2
1
0.5
0.5
3
,
0.5
2
,
0
4
,
0.71
6
,
0.87
Figure 5.61
Increasing
Decreasing
t
y
1
1
0
2
3
2
2
y cos t
B. You’ve just learned how
to graph using
special values and symmetry
f1t2 cos t
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 562 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:

5-61 Section 5.5 Graphs of the Sine and Cosine Functions; Cosecant and Secant Functions 563
C. Graphing yA sin(Bt) and yA cos(Bt)
In many applications, trig functions have maximum and minimum values other than 1
and and periods other than For instance, in tropical regions the maximum and
minimum temperatures may vary by no more than while for desert regions this
difference may be or more. This variation is modeled by the amplitude of sine and
cosine functions.
Amplitude and the Coefficient A (assume B 1)
For functions of the form and let M represent the Maximum
value and m the minimum value of the functions. Then the quantity gives the
average value of the function, while gives the amplitude of the function.
Amplitude is the maximum displacement from the average value in the positive or neg-
ative direction. It is represented by with A playing a role similar to that seen for
algebraic graphs vertically stretches or compresses the graph of f, and reflects
it across the t-axis if Graphs of the form (and ) can quickly
be sketched with any amplitude by noting (1) the zeroes of the function remain fixed
since implies and (2) the maximum and minimum values are A
and respectively, since or implies or Note this
implies the reference rectangle will be 2A units tall and P units wide. Connecting the
points that result with a smooth curve will complete the graph.
EXAMPLE 5
Graphing Where
Draw a sketch of in the interval
Solution
With an amplitude of the reference rectangle will be units tall, by
units wide, centered on the x-axis. Using the rule of fourths, the zeroes are still
, and with the max/min values spaced equally between.
The maximum value is with a minimum value of
. Connecting these points with a “sine curve” gives the
graph shown is also shown for comparison).
Now try Exercises 15 through 20
Period and the Coefficient B
While basic sine and cosine functions have a period of in many applications the
period may be very long (tsunami’s) or very short (electromagnetic waves). For the
equations and the period depends on the value of B. To
see why, consider the function and Table 5.9. Multiplying input valuesy cos12t2
y A cos1Bt2,y A sin1Bt2
2,
Zeroes remain
fixed
y 4 sin t
y sin t
t
4
4
2
2
3
2
1y sin t
4 sin
a
3
2
b 41124
4 sin
a
2
b 4112 4,
t 2,t t 0,
2
2142 8
A
4,
30, 24.y 4 sin t
A 1y A sin t
A.A sin t A1sin t 1A,
A sin t 0,sin t 0
y cos ty sin tA 6 04.
3Af1t2
A
,
M m
2
M m
2
y A cos t,y A sin t
40°
20°,
2.1,
WORTHY OF NOTE
Note that the equations
and
both indicate y is a function
of t, with no reference to
the unit circle definitions
and sin t y.cos t x
y A cos ty A sin t
College Algebra & Trignometry—
cob19529_ch05_557-573.qxd 12/29/08 4:52 PM Page 563 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-5.5:
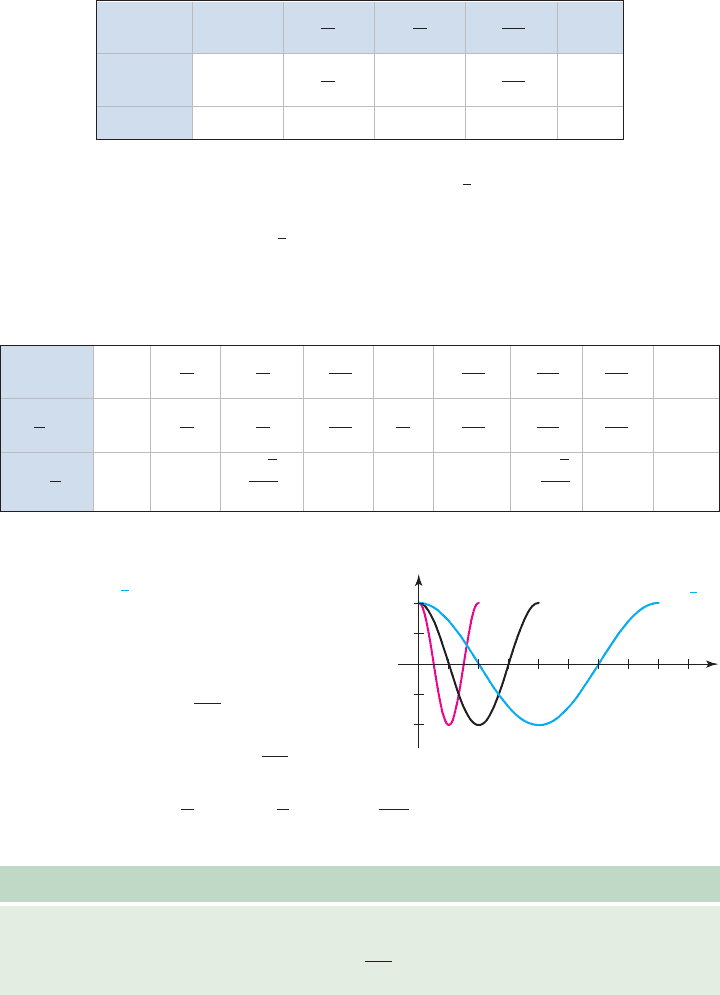
564 CHAPTER 5 An Introduction to Trigonometric Functions 5-62
by 2 means each cycle will be completed twice as fast. The table shows that
completes a full cycle in giving a period of (Figure 5.62,
red graph).
Dividing input values by 2 (or multiplying by will cause the function to
complete a cycle only half as fast, doubling the time required to complete a full
cycle. Table 5.10 shows completes only one-half cycle in (Figure 5.62,
blue graph).
The graphs of
and shown in Figure 5.62
clearly illustrate this relationship and how
the value of B affects the period of a graph.
To find the period for arbitrary values
of B, the formula is used. Note for
and as
shown. For and
Period Formula for Sine and Cosine
For B a real number and functions and
To sketch these functions for periods other than , we still use a reference rectangle
of height 2A and length P, then break the enclosed t-axis in four equal parts to help draw
the graph. In general, if the period is “very large” one full cycle is appropriate for the graph.
If the period is very small, graph at least two cycles.
Note the value of B in Example 6 includes a factor of . This actually happens
quite frequently in applications of the trig functions.
2
P
2
B
.
y A cos1Bt2,y A sin1Bt2
P
2
1/2
4.y cos a
1
2
tb,
B
1
2
,
P
2
2
,y cos12t2, B 2
P
2
B
y cos
A
1
2
t
B
y cos t, y cos12t2,
2
y cos
A
1
2
t
B
1
2
2
P 30, 4,y cos12t2
t 0
2t 0
cos(2t) 10 011
2
3
2
2
3
4
2
4
Table 5.9
Table 5.10
(values in blue are approximate)
t 0
0
1 0.92 0.38 0 10.92
12
2
0.38
12
2
cos a
1
2
tb
7
8
3
4
5
8
2
3
8
4
8
1
2
t
2
7
4
3
2
5
4
3
4
2
4
Figure 5.62
y cos t
y cos(2t)
y
y cos
t
1
2
t
1
1
2 3 4
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 564 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
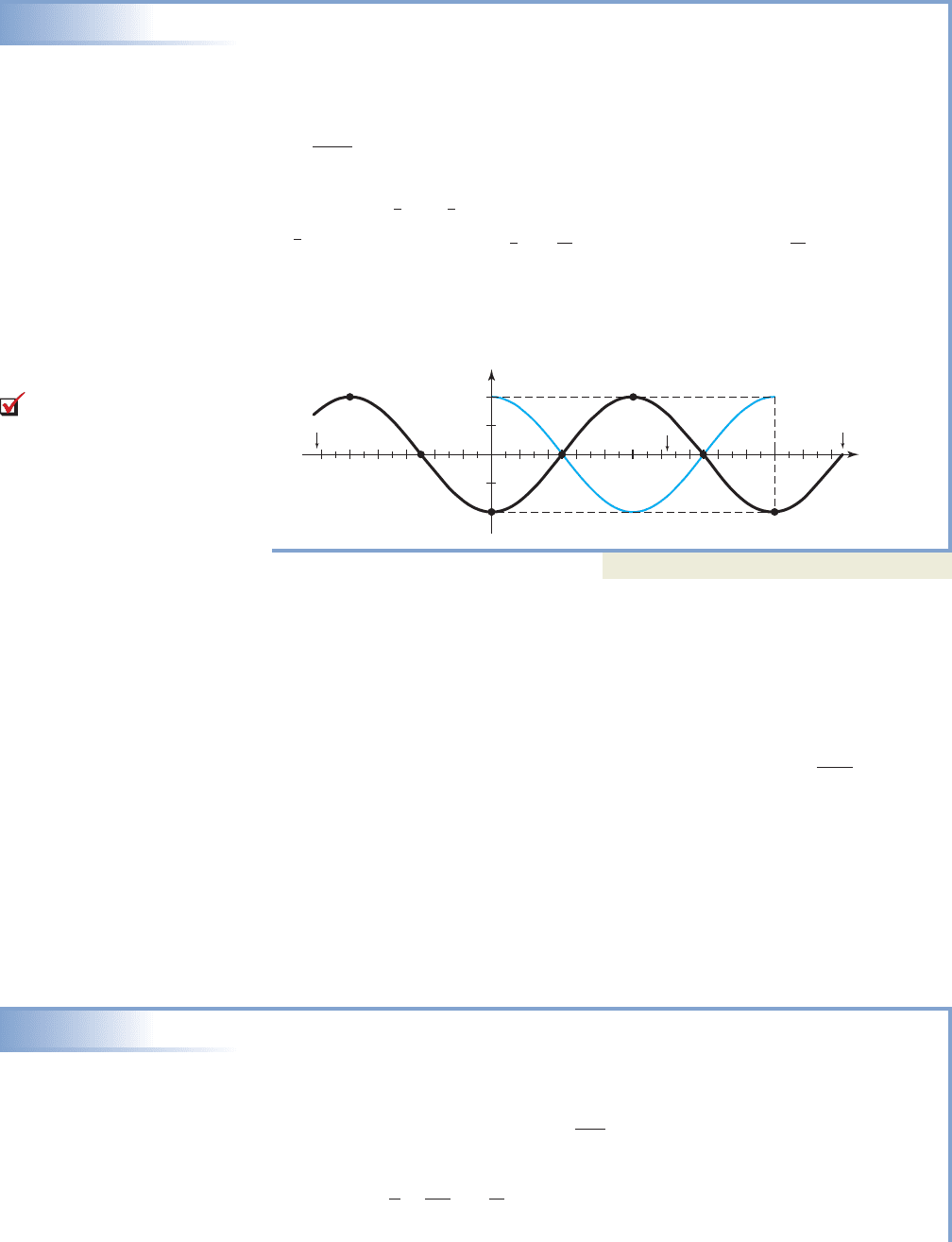
5-63 Section 5.5 Graphs of the Sine and Cosine Functions; Cosecant and Secant Functions 565
EXAMPLE 6
Graphing yAcos(Bt), Where A,
Draw a sketch of for
Solution
The amplitude is so the reference rectangle will be units high.
Since the graph will be vertically reflected across the t-axis. The period is
(note the factors of reduce to 1), so the reference rectangle will
be 5 units in length. Breaking the t-axis into four parts within the frame (rule of
fourths) gives units, indicating that we should scale the t-axis in multiples
of Note the zeroes occur at and with a maximum value at In cases where
the factor reduces, we scale the t-axis as a “standard” number line, and estimate
the location of multiples of For practical reasons, we first draw the unreflected
graph (shown in blue) for guidance in drawing the reflected graph, which is then
extended to fit the given interval.
Now try Exercises 21 through 32
D. Graphs of y csc(Bt) and y sec(Bt)
The graphs of these reciprocal functions follow quite naturally from the graphs of
and by using these observations: (1) you cannot divide
by zero, (2) the reciprocal of a very small number is a very large number (and vice
versa), and (3) the reciprocal of is . Just as with rational functions, division
by zero creates a vertical asymptote, so the graph of will have a
vertical asymptote at every point where This occurs at where k
is an integer Further, when
since the reciprocal of 1 and are still 1 and respectively. Finally, due to obser-
vation 2, the graph of the cosecant function will be increasing when the sine function
is decreasing, and decreasing when the sine function is increasing. In most cases, we
graph by drawing a sketch of then using these observations
as demonstrated in Example 7. In doing so, we discover that the period of the cosecant
function is also and that
EXAMPLE 7
Graphing a Cosecant Function
Graph the function for
Solution
The related sine function is which means we’ll draw a rectangular frame
units high. The period is so the reference frame will be
units in length. Breaking the t-axis into four parts within the frame means each tick
mark will be units apart, with the asymptotes occurring at 0,
and A partial table and the resulting graph are shown.2.
,a
1
4
ba
2
1
b
2
2P
2
1
2,2A 2
y sin t,
t 30, 44.y csc t
y csc1Bt2 is an odd function.2
y sin1Bt2,y csc1Bt2
1,1
csc1Bt21, sin1Bt211p2, , 0, , 2,
p2.
t k,sin t 0.
y csc t
1
sin t
11
y A cos1Bt2,y A sin1Bt2
y 2 cos(0.4t)
y 2cos(0.4t)
t
y
2
1
2
1
1 2345
63 2 1
2
.
10
4
.
15
4
,
5
4
1
4
.
A
1
4
B
5
5
4
P
2
0.4
5
A 6 0
2122 4
A
2,
t in 3, 24.y 2 cos10.4t2
B 1
C. You’ve just learned
how to graph sine and cosine
functions with various
amplitudes and periods
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:49 Page 565

566 CHAPTER 5 An Introduction to Trigonometric Functions 5-64
Now try Exercises 33 and 34
Similar observations can be made regarding and its relationship to
(see Exercises 8, 35, and 36). The most important characteristics of the
cosecant and secant functions are summarized in the following box. For these func-
tions, there is no discussion of amplitude, and no mention is made of their zeroes since
neither graph intersects the t-axis.
Characteristics of f(t) and f(t)
For all real numbers t and integers k,
Domain Range Asymptotes Domain Range Asymptotes
Period Symmetry Period Symmetry
odd even
E. Writing Equations from Graphs
Mathematical concepts are best reinforced by working with them in both “forward and
reverse.” Where graphs are concerned, this means we should attempt to find the equa-
tion of a given graph, rather than only using an equation to sketch the graph. Exercises
of this type require that you become very familiar with the graph’s basic characteris-
tics and how each is expressed as part of the equation.
EXAMPLE 8
Determining the Equation of a Given Graph
The graph shown here is of the form Find the value of A and B.
y A sin(Bt)
y
t
2
2
2
2
⫺
2
3
2
y A sin1Bt2.
sec1t2 sec tcsc1t2csc t
22
t
2
k1q, 14 ´ 31, q2t
2
kt k1q, 14 ´ 31, q2t k
y sec t
y csc t
sec t csc t
y cos1Bt2
y sec1Bt2
t
00
11
2
2
13
1.15
13
2
0.87
3
2
12
1.41
12
2
0.71
4
2
1
2
1
2
0.5
6
1
0
S undefined
csc tsin t
t
y
1
D. You’ve just learned
how to investigate graphs
of the reciprocal functions
f(t) csc(Bt) and f(t) sec(Bt)
College Algebra & Trignometry—
cob19529_ch05_557-573.qxd 12/29/08 4:52 PM Page 566 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-5.5:

5-65 Section 5.5 Graphs of the Sine and Cosine Functions; Cosecant and Secant Functions 567
Solution
By inspection, the graph has an amplitude of and a period of
To find B we used the period formula substituting for P and solving.
period formula
substitute for P;
multiply by 2B
solve for B
The result is which gives us the equation
Now try Exercises 37 through 58
There are a number of interesting applications of this “graph to equation” process
in the exercise set. See Exercises 61 to 72.
y 2 sin
A
4
3
t
B
.B
4
3
,
B
4
3
3 B 4
B 7 0
3
2
3
2
2
B
P
2
B
3
2
P
2
B
,
P
3
2
.A 2
E. You’ve just learned how
to write the equation for a
given graph
Exploring Amplitudes and Periods
TECHNOLOGY HIGHLIGHT
In practice, trig applications offer an immense range of coefficients, creating amplitudes that are
sometimes very large and sometimes extremely small, as well as periods ranging from nanoseconds,
to many years. This Technology Highlight is designed to help you use the calculator more effectively
in the study of these functions. To begin, we note that many calculators offer a preset option
that automatically sets a window size convenient to many trig
graphs. The resulting after pressing 7:ZTrig on
a TI-84 Plus is shown in Figure 5.63 for a calculator set in
Radian .
In Section 5.3 we noted that a change in amplitude will not
change the location of the zeroes or max/min values. On the
screen, enter and
, then use 7:ZTrig to graph the functions.
As you see in Figure 5.64, each graph rises to the expected
amplitude at the expected location, while “holding on” to
the zeroes.
To explore concepts related to the coefficient B and
the period of a trig function, enter and
on the screen and graph using
7:ZTrig. While the result is “acceptable,” the graphs are
difficult to read and compare, so we manually change the
window size to obtain a better view (Figure 5.65).
ZOOM
Y =
Y
2
sin12x2
Y
1
sina
1
2
xb
ZOOM
Y
4
4 sin x
Y
1
1
2
sin x, Y
2
sin x, Y
3
2 sin x,
Y =
MODE
ZOOM
WINDOW
ZOOM
Figure 5.63
6.2
4
4
6.2
Figure 5.64
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 567 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
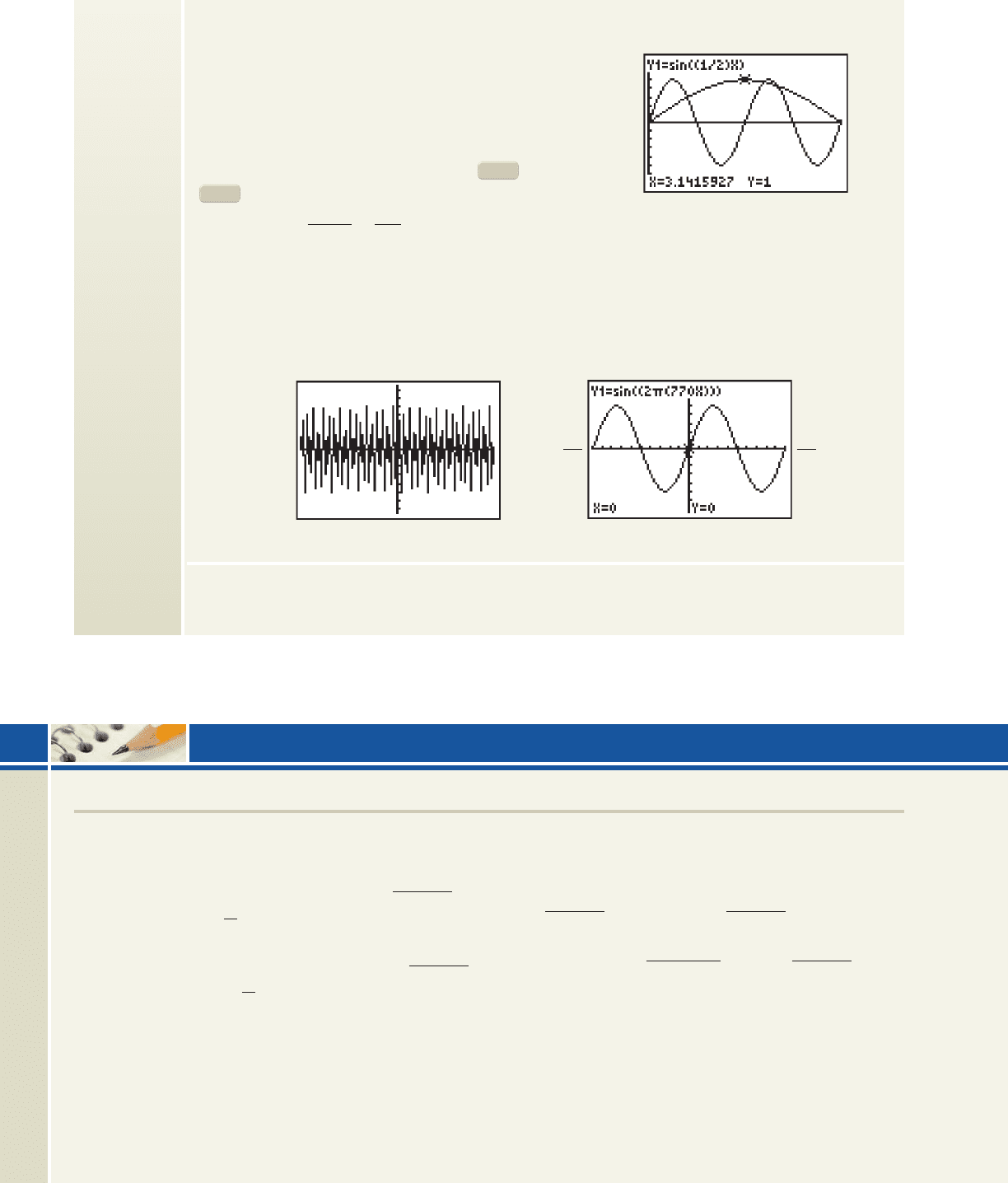
568 CHAPTER 5 An Introduction to Trigonometric Functions 5-66
A true test of effective calculator use comes when the
amplitude or period is a very large or very small number.
For instance, the tone you hear while pressing “5” on your
telephone is actually a combination of the tones modeled
by and Graphing
these functions requires a careful analysis of the period,
otherwise the graph can appear garbled, misleading, or
difficult to read —try graphing Y
1
on the 7:ZTrig or
6:ZStandard screens (see Figure 5.66). First note
and or With a period this short,
even graphing the function from to gives a distorted graph. Setting Xmin to
Xmax to 1/770, and Xscl to (1/770)/10 gives the graph in Figure 5.67, which can be used to
investigate characteristics of the function.
1/770,
Xmax 1Xmin 1
1
770
.P
2
2770
A 1,
ZOOM
ZOOM
Y
2
sin32113362t4.Y
1
sin3217702t4
1.4
1.4
02
Figure 5.65
10
10
10 10
1
770
1
770
1.4
1.4
Figure 5.66
Figure 5.67
Exercise 1: Graph the second tone and find its value at
Exercise 2: Graph the function on a “friendly” window and find the value at x 550.Y
1
950 sin10.005t2
t 0.00025 sec.Y
2
sin32113362t4
5.5 EXERCISES
CONCEPTS AND VOCABULARY
Fill in each blank with the appropriate word or phrase.
Carefully reread the section if needed.
1. For the sine function, output values are in
the interval
2. For the cosine function, output values are
in the interval c0 ,
2
d.
c0,
2
d.
3. For the sine and cosine functions, the domain is
and the range is .
4. The amplitude of sine and cosine is defined to be
the maximum from the value
in the positive and negative directions.
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:50 Page 568

5. Discuss/Describe the four-step process outlined in
this section for the graphing of basic trig functions.
Include a worked-out example and a detailed
explanation.
6. Discuss/Explain how you would determine the
domain and range of Where is this
function undefined? Why? Graph
using What do you notice?y 2 cos12t2.
y 2 sec12t2
y sec x.
5-67 Section 5.5 Graphs of the Sine and Cosine Functions; Cosecant and Secant Functions 569
DEVELOPING YOUR SKILLS
7. Use the symmetry of the unit circle and reference
arcs of standard values to complete a table of
values for in the interval
8. Use the standard values for for
to create a table of values for
on the same interval.
Use the characteristics of to match the given
value of t (a through e) to the correct value of sin t
(I through V).
9. a. b.
c. d.
e. I.
II. III.
IV. V.
10. a. b.
c. d.
e. I.
II. III.
IV. V.
Use steps I through IV given in this section to draw a
sketch of each graph.
11. for
12. for
13. for
14. for t c
2
,
5
2
dy cos t
t c
2
, 2 dy cos t
t 3, 4y sin t
t c
3
2
,
2
dy sin t
sin t 1sin t
12
2
sin t 0sin t
12
2
sin t
1
2
t
25
4
t 19t
23
2
t
11
6
t a
4
12b
sin t
12
2
sin t
12
2
sin t 1sin t
1
2
sin t 0t
21
2
t 13t
15
4
t
4
t a
6
10b
f1t2 sin t
y sec tt 3, 24
y cos t
t 3, 24.y cos t
Use a reference rectangle and the rule of fourths to
draw an accurate sketch of the following functions
through two complete cycles—one where and
one where Clearly state the amplitude and
period as you begin.
15. 16.
17. 18.
19. 20.
21. 22.
23. 24.
25. 26.
27. 28.
29. 30.
31. 32.
Draw the graph of each function by first sketching the
related sine and cosine graphs, and applying the
observations made in this section.
33. 34.
35. 36.
Clearly state the amplitude and period of each function,
then match it with the corresponding graph.
37. 38.
39. 40.
41. 42.
43. 44.
45. 46. y csc112t2y sec18t2
g1t2
7
4
cos10.8t2f 1t2
3
4
cos10.4t2
y 2 sec
a
1
4
tby 2 csc a
1
2
tb
y 3 cos12t2y 3 sin12t2
y 2 sin14t2y 2 cos14t2
f
1t2 3 sec12t2y 2 sec t
g1t2 2 csc14t2y 3 csc t
g1t2 3 cos1184t2f 1t2 2 sin1256t2
y 2.5 cos
a
2
5
tby 4 sin a
5
3
tb
g1t2 5 cos18t2f1t2 3 sin14t2
y 3 cosa
3
4
tbf1t2 4 cos a
1
2
tb
y 1.7 sin14t2y 0.8 cos12t2
y cos12t2y sin12t2
y
3
4
sin ty
1
2
sin t
y 3 cos ty 2 cos t
y 4 sin ty 3 sin t
t 0.
t 0,
College Algebra & Trignometry—
cob19529_ch05_557-573.qxd 12/29/08 4:52 PM Page 569 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-5.5:
