Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.

Fill in each blank with the appropriate word or phrase.
Carefully reread the section if needed.
1. A central circle is symmetric to the axis, the
axis and to the .
2. Since is on the unit circle, the point
in QII is also on the circle.
3. On a unit circle, , ,
and ; while ,
, and .
x
y
1
y
1
x
tan t
sin t cos t
1
5
13
,
12
13
2
4. On a unit circle with in radians, the length of a(n)
is numerically the same as the
measure of the , since for
when
5. Discuss/Explain how knowing only one point on
the unit circle, actually gives the location of four
points. Why is this helpful to a study of the circular
functions?
6. A student is asked to find t using a calculator, given
with t in QII. The answer submitted
is Discuss/Explain why
this answer is not correct. What is the correct
response?
t sin
1
0.5592 34°.
sin t 0.5592
r 1.
s r, s
5.4 EXERCISES
CONCEPTS AND VOCABULARY
550 CHAPTER 5 An Introduction to Trigonometric Functions 5-48
Given the point is on a unit circle, complete the ordered
pair (x, y) for the quadrant indicated. For Exercises 7 to
14, answer in radical form as needed. For Exercises 15
to 18, round results to four decimal places.
7. QIII 8. QII
9. QIV 10. ; QIV
11. ; QI 12. ; QIII
13. ; QII 14. ; QIax,
16
5
ba
111
4
, yb
ax,
113
7
ba
111
6
, yb
ax,
8
17
ba
5
13
, yb;
10.6, y2;1x, 0.82;
15. ; QIII 16. (0.9909, y); QIV
17. (x, 0.1198); QII 18. (0.5449, y); QI
Verify the point given is on a unit circle, then use
symmetry to find three more points on the circle.
Results for Exercises 19 to 22 are exact, results for
Exercises 23 to 26 are approximate.
19. 20.
21. 22. a
16
3
,
13
3
ba
111
6
,
5
6
b
a
17
4
,
3
4
ba
13
2
,
1
2
b
1x, 0.21372
DEVELOPING YOUR SKILLS
College Algebra & Trignometry—
E. You’ve just learned how
to find the real number t
corresponding to given values
of sin t, cos t, and tan t
t sin t cos t tan t csc t sec t cot t
0 0 1 0 undefined 1 undefined
2
11
2
1 0 undefined 1 undefined 0
2
1
13
13
3
2
13
213
3
13
1
2
13
2
3
12
12
12
2
12
2
4
13
2
13
213
3
1
13
13
3
13
2
1
2
6
cob19529_ch05_503-614.qxd 11/11/08 1:48 PM Page 550 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
23. (0.3325, 0.9431) 24.
25. 26.
27. Use a triangle with a hypotenuse of length
1 to verify that is a point on the unit circle.
28. Use the results from Exercise 27 to find three
additional points on the circle and name the
quadrant of each point.
Find the reference angle associated with each rotation,
then find the associated point (x, y) on the unit circle.
29. 30.
31. 32.
33. 34.
35. 36.
Without the use of a calculator, state the exact value
of the trig functions for the given angle. A diagram
may help.
37. a. b.
c. d.
e. f.
g. h.
38. a. b.
c. d.
e. f.
g. h.
39. a. b. cos 0
c. d. cosa
3
2
bcosa
2
b
cos
tana
10
3
btana
4
3
b
tana
3
btana
7
3
b
tana
5
3
btana
4
3
b
tana
2
3
btana
3
b
sina
11
4
bsina
5
4
b
sina
4
bsina
9
4
b
sina
7
4
bsina
5
4
b
sina
3
4
bsina
4
b
39
4
25
6
11
3
11
4
7
4
5
6
5
3
5
4
a
1
2
,
13
2
b
6
:
3
:
2
10.2029, 0.9792210.9937, 0.11212
10.7707, 0.63722 40. a. b. sin 0
c. d.
Use the symmetry of the circle and reference arcs as
needed to state the exact value of the trig functions for
the given real number, without the use of a calculator. A
diagram may help.
41. a. b.
c. d.
e. f.
g. h.
42. a. b.
c. d.
e. f.
g. h.
43. a. b. tan 0
c. d.
44. a. b. cot 0
c. d.
Given (x, y) is a point on a unit circle corresponding to t,
find the value of all six circular functions of t.
45.
46.
x
y
t
(1, 0)
,
15
17
8
17
x
y
t
(1, 0)
(0.8, 0.6)
cota
3
2
bcota
2
b
cot
tana
3
2
btana
2
b
tan
csca
17
6
bcsca
11
6
b
csca
6
bcsca
13
6
b
csca
11
6
bcsca
7
6
b
csca
5
6
bcsca
6
b
cosa
23
6
bcosa
5
6
b
cosa
6
bcosa
13
6
b
cosa
11
6
bcosa
7
6
b
cosa
5
6
bcosa
6
b
sina
3
2
bsina
2
b
sin
5-49 Section 5.4 Unit Circles and the Trigonometry of Real Numbers 551
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:44 Page 551
47.
48.
49.
50.
51. 52.
53. 54.
55. 56.
57. 58.
On a unit circle, the real number t can represent either
the amount of rotation or the length of the arc when we
associate t with a point (x, y) on the circle. In the circle
diagram shown, the real number t in radians is marked
off along the circumference. For Exercises 59 through
70, name the quadrant in which t terminates and use the
a
12
3
,
17
3
ba
12
2
,
12
2
b
a
13
2
,
1
2
ba
1
2
,
13
2
b
a
216
5
,
1
5
ba
1
3
,
212
3
b
a
17
4
,
3
4
ba
2
5
,
121
5
b
x
y
t
(1, 0)
,
2
3
√5
3
x
y
t
(1, 0)
,
5
6
√11
6
x
y
t
(1, 0)
,
24
25
7
25
x
y
t
(1, 0)
,
5
13
12
13
figure to estimate function values to one decimal place
(use a straightedge). Check results using a calculator.
59. sin 0.75 60. cos 2.75
61. cos 5.5 62. sin 4.0
63. tan 0.8 64. sec 3.75
65. csc 2.0 66. cot 0.5
67. 68.
69. 70.
Without using a calculator, find the value of t in [0, )
that corresponds to the following functions.
71. ; t in QII
72. ; t in QIV
73. ; t in QIII
74. ; t in QIV
75. ; t in QII
76. ; t in QIII
77. ; t is quadrantal
78. ; t is quadrantalcos t 1
sin t 1
sec t 2
tan t 13
sin t
1
2
cos t
23
2
cos t
1
2
sin t
13
2
2
seca
8
5
btana
8
5
b
sina
5
8
bcosa
5
8
b
x
y
1
5.0
5.5
6.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
0.8
0
0.60.40.2
1
0.2
0.4
0.6
0.8
q
2
3
0
552 CHAPTER 5 An Introduction to Trigonometric Functions 5-50
Exercises 59 to 70
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:45 Page 552

Without using a calculator, find the two values
of t (where possible) in [0, ) that make each
equation true.
79. 80.
81. tan t undefined 82. csc t undefined
83. 84.
85. 86.
87. Given is a point on the unit circle that
corresponds to t. Find the coordinates of the point
corresponding to (a) and (b)
t .t
1
3
4
,
4
5
2
cos t 1sin t 0
sin t
12
2
cos t
12
2
csc t
2
13
sec t 12
2
88. Given is a point on the unit circle that
corresponds to t. Find the coordinates of the point
corresponding to (a) and (b)
Find an additional value of t in [0, ) that makes the
equation true.
89.
90.
91.
92.
93.
94.
sec 5.7 1.1980
tan 0.4 0.4228
sin 5.23 0.8690
cos 4.5 0.2108
cos 2.12 0.5220
sin 0.8 0.7174
2
t .t
1
7
25
,
24
25
2
5-51 Section 5.4 Unit Circles and the Trigonometry of Real Numbers 553
WORKING WITH FORMULAS
95. From Pythagorean triples to points on the
unit circle:
While not strictly a “formula,” dividing a
Pythagorean triple by r is a simple algorithm for
rewriting any Pythagorean triple as a triple with
hypotenuse 1. This enables us to identify certain
points on a unit circle, and to evaluate the six trig
functions of the related acute angle. Rewrite each
triple as a triple with hypotenuse 1, verify is
a point on the unit circle, and evaluate the six trig
functions using this point.
a. (5, 12, 13) b. (7, 24, 25)
c. (12, 35, 37) d. (9, 40, 41)
a
x
r
,
y
r
b
1x, y, r2S a
x
r
,
y
r
, 1b
96. The sine and cosine of ;
In the solution to Example 8(a), we mentioned
were standard values for sine and cosine,
“related to certain multiples of .” Actually, we
meant “odd multiples of ” The odd multiples of
are given by the “formula” shown, where k is
any integer. (a) What multiples of are generated
by , 0, 1, 2, 3? (b) Find similar
formulas for Example 8(b), where is a standard
value for tangent and cotangent, “related to certain
multiples of .”
6
13
k 3, 2, 1
4
4
4
.
4
12
2
k 12k 12
4
APPLICATIONS
97. Laying new sod:
When new sod is laid,
a heavy roller is used
to press the sod down
to ensure good contact
with the ground
beneath. The radius of
the roller is 1 ft.
(a) Through what angle
(in radians) has the
roller turned after
being pulled across 5 ft of yard? (b) What angle
must the roller turn through to press a length
of 30 ft?
98. Cable winch: A large
winch with a radius of
1 ft winds in 3 ft of
cable. (a) Through
what angle (in radians)
has it turned? (b) What
angle must it turn
through in order to
winch in 12.5 ft of cable?
99. Wiring an apartment: In the wiring of an
apartment complex, electrical wire is being pulled
from a spool with radius 1 decimeter
1 ft
Exercise 98
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 9:25 PM Page 553 epg HD 049:Desktop Folder:11/11/08:Coburn_do_t del-ch05:

( ). (a) What length (in decimeters) is
removed as the spool turns through 5 rad? (b) How
many decimeters are removed in one complete turn
of the spool?
100. Barrel races: In the barrel
races popular at some family
reunions, contestants stand on
a hard rubber barrel with a
radius of 1 cubit
( ), and try to
“walk the barrel” from the
start line to the finish line
without falling. (a) What
distance (in cubits) is traveled
as the barrel is walked
through an angle of 4.5 rad?
(b) If the race is 25 cubits
long, through what angle will the winning barrel
walker walk the barrel?
Interplanetary measurement: In the year 1905,
astronomers began using astronomical units or AU to study
the distances between the celestial bodies of our solar
system. One AU represents the average distance between
the Earth and the Sun, which is about 93 million miles.
Pluto is roughly 39.24 AU from the Sun.
101. If the Earth travels through an angle of 2.5 rad
about the Sun, (a) what distance in astronomical
units (AU) has it traveled? (b) How many AU does
it take for one complete orbit around the Sun?
102. If you include the dwarf planet Pluto, Jupiter is the
middle (fifth of nine) planet from the Sun. Suppose
astronomers had decided to use its average distance
1 cubit 18 in.
1t 22
1 dm 10 cm from the Sun as 1 AU. In this case, 1 AU would be
480 million miles. If Jupiter travels through an
angle of 4 rad about the Sun, (a) what distance in
the “new” astronomical units (AU) has it traveled?
(b) How many of the new AU does it take to
complete one-half an orbit about the Sun? (c) What
distance in the new AU is the dwarf planet Pluto
from the Sun?
103. Compact disk circumference:A standard compact
disk has a radius of 6 cm. Call this length “1 unit.”
Mark a starting point on any large surface, then
carefully roll the compact disk along this line
without slippage, through one full revolution
( rad) and mark this spot. Take an accurate
measurement of the resulting line segment. Is the
result close to “units” ( )?
104. Verifying :
On a protractor,
carefully measure
the distance from
the middle of the
protractor’s eye to
the edge of the
protractor along the
mark, to the
nearest half-millimeter. Call this length “1 unit.”
Then use a ruler to draw a straight line on a blank
sheet of paper, and with the protractor on edge,
start the zero degree mark at one end of the line,
carefully roll the protractor until it reaches 1 radian
, and mark this spot. Now measure the
length of the line segment created. Is it very close
to 1 “unit” long?
157.3°2
0°
s r
2 6 cm2
2
554 CHAPTER 5 An Introduction to Trigonometric Functions 5-52
80
90
90
70
60
50
40
30
20
10
100
110
120
130
140
150
160
170
180
0
100
110
120
130
140
150
160
170
80
70
60
50
40
30
20
10
0
180
eye
1 unit
EXTENDING THE CONCEPT
105. In this section, we discussed the domain of the
circular functions, but said very little about their
range. Review the concepts presented here and
determine the range of and . In
other words, what are the smallest and largest
output values we can expect?
106. Since what can you say about the
range of the tangent function?
tan t
sin t
cos t
,
y sin ty cos t
Use the radian grid given with Exercises 59–70 to
answer Exercises 107 and 108.
107. Given with the terminal side of the
arc in QII, (a) what is the value of 2t? (b) What
quadrant is t in? (c) What is the value of cos t?
(d) Does ?
108. Given with the terminal side of the
arc in QIII, (a) what is the value of 2t? (b) What
quadrant is t in? (c) What is the value of sin t?
(d) Does ?sin12t2 2sin t
sin12t20.8
cos12t2 2cos t
cos12t20.6
College Algebra & Trignometry—
Exercise 104
cob19529_ch05_503-614.qxd 11/11/08 1:48 PM Page 554 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
MAINTAINING YOUR SKILLS
111. (1.3) Solve each equation:
a.
b.
112. (3.2) Use the rational zeroes theorem to solve the
equation completely, given is one root.
x
4
x
3
3x
2
3x 18 0
x 3
21x 1
3 7
2
x 1
3 7
5-53 Mid-Chapter Check 555
109. (2.1) Given the points ( , 4) and (5, 2) find
a. the distance between them
b. the midpoint between them
c. the slope of the line through them.
110. (4.3) Use a calculator to find the value of each
expression, then explain the results.
a. ______
b. ______log 20 log 2
log 2 log 5
3
MID-CHAPTER CHECK
1. The city of Las Vegas, Nevada, is located at
north latitude, west
longitude. (a) Convert both measures to decimal
degrees. (b) If the radius of
the Earth is 3960 mi, how far
north of the equator is Las
Vegas?
2. Find the angle subtended by
the arc shown in the figure,
then determine the area of the
sector.
3. Evaluate without using a
calculator: (a)
and (b) .
4. Evaluate using a calculator: (a) and
(b) tan .
5. Complete the ordered pair
indicated on the unit circle in
the figure and find the value of
all six trigonometric functions
at this point.
6. For the point on the unit
circle in Exercise 5, find the
related angle t in both degrees
(to tenths) and radians
(to ten-thousandths).
83.6°
sec
a
12
b
sin
a
7
4
b
cot 60°
115°04¿48–36°06¿36–
7. Use the special
triangle to state the
length of side b
and hypotenuse c.
8. From a distance of
325 ft, the angle of
elevation from eye
level to the top of the world’s tallest tree is . If
the person taking the sighting is 6 ft tall, how tall is
the tree to the nearest foot?
9. On a unit circle, if arc t has length 5.94, (a) in what
quadrant does it terminate? (b) What is its reference
arc? (c) Of sin t, cos t, and tan t, which are negative
for this value of t?
10. At a high school gym, sightings are taken from the
basketball half-court line to help determine the
height of the backboard. The angle of elevation to
the top of the backboard is while the angle of
elevation to the bottom of the backboard is
If the half-court line is 40 ft away, how tall is the
backboard? Answer in feet and inches to the
nearest inch.
13.4°.
18°,
48°
x
y
86 cm
20 cm
x
y
t
1
√5
3
,
y
Exercise 2
Exercise 5
b
c
60
30
7 cm
Exercise 7
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:45 Page 555

556 CHAPTER 5 An Introduction to Trigonometric Functions 5-54
Trigonometry of the Real Numbers and the Wrapping Function
The circular functions are sometimes discussed in terms of what is called a wrapping function, in which the real number
line is literally wrapped around the unit circle. This approach can help illustrate how the trig functions can be seen as func-
tions of the real numbers, and apart from any reference to a right triangle. Figure 5.49 shows (1) a unit circle with the
location of certain points on the circumference clearly marked and (2) a number line that has been marked in multiples of
to coincide with the length of the special arcs (integers are shown in the background). Figure 5.50 shows this same
number line wrapped counterclockwise around the unit circle in the positive direction. Note how the resulting diagram
confirms that an arc of length is associated with the point on the unit circle: and
; while an arc of length of is associated with the point and sin .
Use this information to complete the exercises given.
1. What is the ordered pair associated with an arc length of ? What is the value of cos t? sin t?
2. What arc length t is associated with the ordered pair ? Is cos t positive or negative? Why?
3. If we continued to wrap this number line all the way around the circle, in what quadrant would an arc length of
terminate? Would sin t be positive or negative?
4. Suppose we wrapped a number line with negative values clockwise around the unit circle. In what quadrant would
an arc length of terminate? What is cos t? sin t? What positive rotation terminates at the same point?
t
5
3
t
11
6
a
13
2
,
1
2
b
t
2
3
y
x
,
1
2
√3
2
,
2
√2
2
√2
,
2
√2
2
√2
1
2
,
2
√3
,
2
1
2
√3
,
2
1
2
√3
(1, 0)
(0, 1)
0
12
123
5
12
11
12
2
3
3
4
5
6
7
12
6
4
3
2
t
4
45
5
6
1
2
a
13
2
,
1
2
b: cos
5
6
13
2
t
5
6
sin
4
12
2
cos
4
12
2
a
12
2
,
12
2
bt
4
12
REINFORCING BASIC CONCEPTS
Figure 5.49
y
x
0
4
45
12
6
4
3
2
5
12
7
12
2
3
3
4
5
6
11
12
3
2
1
Figure 5.50
College Algebra & Trignometry—
cob19529_ch05_542-556.qxd 11/12/08 12:01 AM Page 556 epg HD 049:System Folder:Appearance:Coburn Don't del-book 2 :Coburn_do_t del-ch05:

Figure 5.51
As with the graphs of other functions, trigonometric graphs contribute a great deal
toward the understanding of each trig function and its applications. For now, our
primary interest is the general shape of each basic graph and some of the transforma-
tions that can be applied. We will also learn to analyze each graph, and to capitalize
on the features that enable us to apply the functions as real-world models.
A. Graphing f(t) sin t
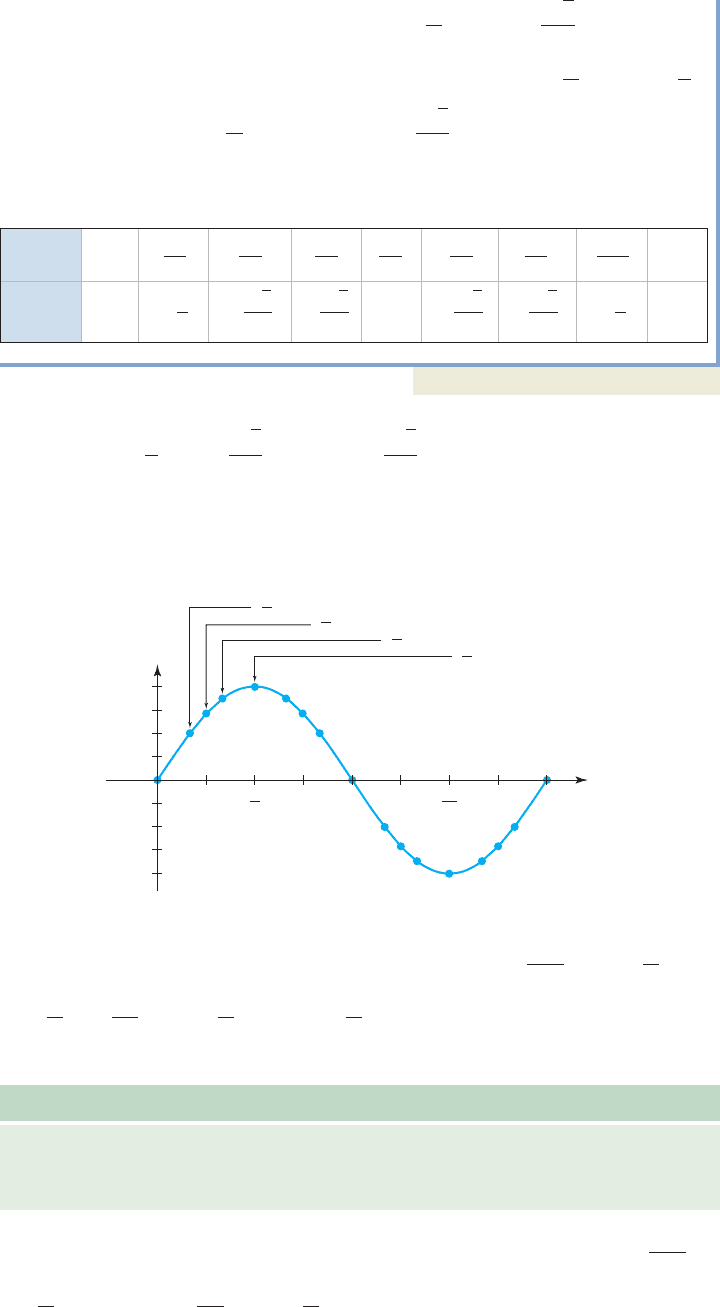
Consider the following table of values (Table 5.4) for sin t and the special angles in QI.
Observe that in this interval, sine values are increasing from 0 to 1. From to
(QII), special values taken from the unit circle show sine values are decreasing from
1 to 0, but through the same output values as in QI. See Figures 5.51 through 5.53.
2
5-55 557
Learning Objectives
In Section 5.5 you will learn how to:
A. Graph using
special values and
symmetry
B. Graph using
special values and
symmetry
C. Graph sine and cosine
functions with various
amplitudes and periods
D. Investigate graphs of
the reciprocal functions
and
E. Write the equation for a
given graph
f1t2 sec 1Bt2
f1t2 csc 1Bt2
f1t2 cos t
f1t2 sin t
5.5 Graphs of the Sine and Cosine Functions;
Cosecant and Secant Functions
Table 5.4
t 0
01
13
2
12
2
1
2
sin t
2
3
4
6
(1, 0) (1, 0)
(0, 1)
x
y
,
2
1
2
√3
2
3
Figure 5.53
(1, 0) (1, 0)
(0, 1)
x
y
5
6
2
√3
2
1
,
Figure 5.52
(1, 0) (1, 0)
(0, 1)
x
y
3
4
,
2
√2
2
√2
sin a
2
3
b
23
2
sin
a
5
6
b
1
2
sin a
3
4
b
22
2
With this information we can extend our table of values through noting that
(see Table 5.5).
Using the symmetry of the circle and the fact that y is negative in QIII and QIV,
we can complete the table for values between and
EXAMPLE 1
Finding Function Values Using Symmetry
Use the symmetry of the unit circle and reference arcs of special values to
complete Table 5.6. Recall that y is negative in QIII and QIV.
2.
sin 0
,
Table 5.5
t 0
01 0
1
2
12
2
13
2
13
2
12
2
1
2
sin t
5
6
3
4
2
3
2
3
4
6
Table 5.6
t
sin t
2
11
6
7
4
5
3
3
2
4
3
5
4
7
6
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 557 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
558 CHAPTER 5 An Introduction to Trigonometric Functions 5-56
Solution
Symmetry shows that for any odd multiple of depending on
the quadrant of the terminal side. Similarly, for any reference arc of
while any reference arc of will give . The completed table is
shown in Table 5.7.
Now try Exercises 7 and 8
Noting that and we plot these points and
connect them with a smooth curve to graph in the interval The first
five plotted points are labeled in Figure 5.54.
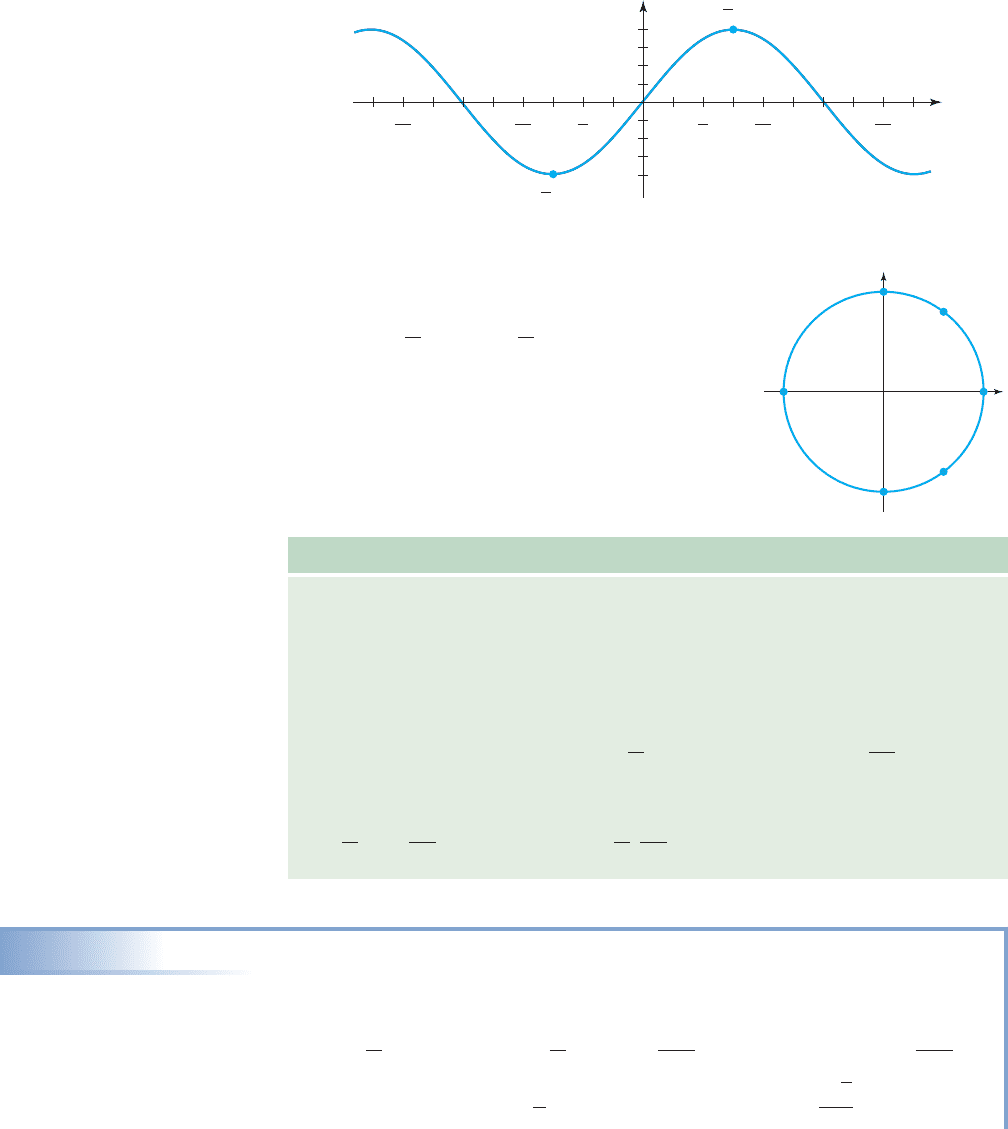
Expanding the table from to using reference arcs and the unit circle
shows that function values begin to repeat. For example, since
since and so on. Functions that cycle through a
set pattern of values are said to be periodic functions.
Periodic Functions
A function f is said to be periodic if there is a positive number P such that
for all t in the domain. The smallest number P for which this occurs
is called the period of f.
For the sine function we have as in
and with the idea extending to all other real sin
a
9
4
b sin a
4
2b,sin a
6
2b
sin
a
13
6
b sin t sin1t 22,
f 1t P2 f 1t2
r
4
,
r
6
; sin a
9
4
b sin a
4
b
sin
a
13
6
b sin a
6
b
42
30, 24.y sin t
13
2
0.87,
12
2
0.71,
1
2
0.5,
sin t
13
2
3
sin t
1
2
,
6
,
sin t
12
2
t
4
,
Table 5.7
t
0 10
1
2
12
2
13
2
13
2
12
2
1
2
sin t
2
11
6
7
4
5
3
3
2
4
3
5
4
7
6
Figure 5.54
D
e
c
r
e
a
s
i
n
g
I
n
c
r
e
a
s
i
ng
sin t
1
2
3
2
t
2
1
0.5
0.5
(0, 0)
6
,
0.5
4
,
0.71
3
,
0.87
2
,
1
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:49 PM Page 558 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
5-57 Section 5.5 Graphs of the Sine and Cosine Functions; Cosecant and Secant Functions 559
numbers t: for all integers k. The sine function is periodic with
period
Although we initially focused on positive values of t in and
are certainly possibilities and we note the graph of extends infinitely in both
directions (see Figure 5.55).
Finally, both the graph and the unit circle confirm
that the range of is , and that
is an odd function. In particular, the graph
shows , and the unit circle
shows (Figure 5.56) , and ,
from which we obtain by substitu-
tion. As a handy reference, the following box summa-
rizes the main characteristics of
Characteristics of f(t) sin t
For all real numbers t and integers k,
Domain Range Period
Symmetry Maximum value Minimum value
odd
Increasing Decreasing Zeroes
EXAMPLE 2
Using the Period of sin t to Find Function Values
Use the characteristics of to match the given value of t to the correct
value of sin t.
a. b. c. d. e.
I. II. III. IV. V. sin t 0sin t
12
2
sin t 1sin t
1
2
sin t 1
t
11
2
t 21t
17
2
t
6
t a
4
8b
f 1t2 sin t
t ka
2
,
3
2
b
a0,
2
b ´ a
3
2
, 2b
at t
3
2
2kat t
2
2ksin1t2sin t
sin t 1sin t 1
231, 141q, q2
y sin t.
sin1t2sin t
sin1t2ysin t y
sina
2
bsina
2
b
y sin t
31, 14y sin t
y sin t
k 6 0
30, 24, t 6 0
P 2.
sin t sin1t 2k2
Figure 5.55
Figure 5.56
y sin t
t
y
0.5
1
1
0.5
42
4
3
2
3
3
3
3 3
,
1
2
,
1
2
x
y
(0, 1)
(1, 0) (1, 0)
(0, 1)
(x, y)
(x, y)
t
t
y sin t
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:48 Page 559
