Coburn J.W. Algebra and Trigonometry
Подождите немного. Документ загружается.


85. Height of a
rainbow: While
visiting the
Lapahoehoe
Memorial on
the island of
Hawaii, Bruce
and Carma see a
spectacularly
vivid rainbow
arching over the
bay. Bruce
speculates the
rainbow is 500 ft
away, while
Carma estimates the angle of elevation to the
highest point of the rainbow is about . What
was the approximate height of the rainbow?
86. High-wire walking: As part of a circus act, a
high-wire walker not only “walks the wire,” she
walks a wire that is set at an incline of to the
horizontal! If the length of the (inclined) wire is
10°
42°
25.39 m, (a) how much higher is the wire set at the
destination pole than at the departure pole?
(b) How far apart are the poles?
87. Diagonal of a cube:
A cubical box has a
diagonal measure of 35
cm. (a) Find the
dimensions of the box
and (b) the angle that
the diagonal makes at the
lower corner of the box.
88. Diagonal of a rectangular parallelepiped:
A rectangular box has a width of 50 cm and a
length of 70 cm. (a) Find the height h that ensures
the diagonal across the
middle of the box will be
90 cm and (b) the angle
that the diagonal makes at
the lower corner of the
box.
x
x
x
d 35 cm
530 CHAPTER 5 An Introduction to Trigonometric Functions 5-28
h
70 cm
50
EXTENDING THE CONCEPT
89. The formula
can be used to calculate the
height h of a building when
distance x is unknown but
distance d is known (see the
diagram). Use the ratios for
cot u and cot v to derive the
formula (note x is “absent” from the formula).
90. Use the diagram given to derive a formula for the
height h of the taller building in terms of the height
x of the shorter building and the ratios for tan u and
tan v. Then use the formula to find h given the
shorter building is 75 m tall with and
v 50°.
u 40°
h
dx d
uv
x
h
d
cot u cot v
91. The radius of the Earth
at the equator ( N
latitude) is
approximately 3960
mi. Beijing, China, is
located at N
latitude, E
longitude.
Philadelphia,
Pennsylvania, is
located at the same
latitude, but at W
longitude. (a) Use the
diagram given and a cofunction relationship to
find the radius r of the Earth (parallel to the
equator) at this latitude; (b) use the arc length
formula to compute the shortest distance
between these two cities along this latitude; and
(c) if the supersonic Concorde flew a direct flight
between Beijing and Philadelphia along this
latitude, approximate the flight time assuming a
cruising speed of 1250 mph. Note: The shortest
distance is actually traversed by heading northward,
using the arc of a “great circle” that goes through
these two cities.
75°
116°
39.5°
0°
N
R
r
h
R h
R
North Pole
South Pole
College Algebra & Trignometry—
h
d
u
v
x
cob19529_ch05_519-531.qxd 12/29/08 4:49 PM Page 530 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-5.2:

MAINTAINING YOUR SKILLS
94. (5.1) The armature for the
rear windshield wiper has
a length of 24 in., with a
rubber wiper blade that is
20 in. long. What area of
my rear windshield is
cleaned as the armature swings back-and-forth
through an angle of ?
95.
(5.1) The boxes used to ship
some washing machines are
perfect cubes with edges
measuring 38 in. Use a special
triangle to find the length of the
diagonal d of one side, and the
length of the interior diagonal D
(through the middle of the box).
d
D
110°
5-29 Section 5.3 Trigonometry and the Coordinate Plane 531
92. (1.5) Solve by factoring:
a.
b.
c.
d.
e.
93.
(2.5) For the graph of T(x)
given, (a) name the local
maximums and minimums,
(b) the zeroes of T,
(c) intervals where
and and
(d) intervals where and .
T1x26 0T1x27 0
T1x2c,T1x2T
x
y
T(x)
55
3
3
g
3
9g
2
10g 90 0
g
2
9g 10 0
g
2
9g 10 0
g
2
9 0
g
2
9g 0
This section tends to bridge the study of static trigonometry and the angles of a right tri-
angle, with the study of dynamic trigonometry and the unit circle. This is accomplished
by noting that the domain of the trig functions (unlike a triangle point of view) need not
be restricted to acute angles. We’ll soon see that the domain can be extended to include
trig functions of any angle, a view that greatly facilitates our work in Chapter 7, where
many applications involve angles greater than .
A. Trigonometric Ratios and the Point P(x, y)
Regardless of where a right triangle is situated or how it
is oriented, each trig function can be defined as a given
ratio of sides with respect to a given angle. In this light,
consider a 30-60-90 triangle placed in the first quadrant
with the angle at the origin and the longer side along
the x-axis. From our previous review of similar triangles,
the trig ratios will have the same value regardless of the
triangle’s size so for convenience, we’ll use a hypotenuse
of 10. This gives sides of 5, and 10, and from the
diagram in Figure 5.22 we note the point (x, y) marking
the vertex of the angle has coordinates ( 5).
Further, the diagram shows that and can all be expressed in
terms of these coordinates since and
where r is the length of the hypotenuse. Each result
reduces to the more familiar values seen earlier: and
. This suggests we can define the six trig functions in terms
of x, y, and r, where .
r 2x
2
y
2
tan 30°
1
13
13
3
sin 30°
1
2
, cos 30°
13
2
,
opp
adj
5
513
y
x
1tangent2,
opp
hyp
5
10
y
r
1sine2,
adj
hyp
513
10
x
r
1cosine2,
tan 30°cos 30°,sin 30°,
513
,
60°
513
,
30°
90°
5.3 Trigonometry and the Coordinate Plane
Learning Objectives
In Section 5.3 you will learn how to:
A. Define the trigonometric
functions using the
coordinates of a point
in QI
B. Use reference angles to
evaluate the trig
functions for any angle
C. Solve applications using
the trig functions of any
angle
5
5
10
30
60
10
x
y
(5√3, 5)
5√3
Figure 5.22
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 9:03 PM Page 531 epg HD 049:Desktop Folder:11/11/08:Coburn_do_t del-ch05:

532 CHAPTER 5 An Introduction to Trigonometric Functions 5-30
Consider that the slope of the line coincident with the hypotenuse is
and since the line goes through the origin its equation must be
Any point (x, y) on this line will be at the vertex of a right triangle
formed by drawing a perpendicular line from the point (x, y) to the x-axis. As Example 1
shows, we obtain the special values for and regardless of the
point chosen.
EXAMPLE 1
Evaluating Trig Functions Using x, y, and r
Pick an arbitrary point in QI that satisfies
then draw the corresponding right triangle and
evaluate and
Solution
The coefficient of x has a denominator of 3, so we
choose a multiple of 3 for convenience. For
we have As seen in the figure,
the point (6, ) is on the line and at the vertex
of the angle. Evaluating the trig functions at
we obtain:
Now try Exercises 7 and 8
In general, consider any two points (x, y) and (X, Y) on an arbitrary line at
corresponding distances r and R from the origin (Figure 5.23). Because the triangles
formed are similar, we have and so on, and we conclude that the value
of the trig functions are indeed independent of the point chosen.
Viewing the trig functions in terms of x, y, and r produces significant results. In
Figure 5.24, we note the line from Example 1 also extends into QIII, and
creates another angle whose vertex is at the origin (since vertical angles are equal).
The sine, cosine, and tangent functions can still be evaluated for this angle, but in QIII
30°
y
13
3
x
x
y
10
6
10
(6, 2√3)
(6, 2√3)
2√3
4√3
y
3
√3
x
210
30
x
x
X
r
y
Y
y
(x, y)
(X, Y)
y kx
y
x
Y
X
,
x
r
X
R
,
y kx,
13
3
613
41313
13
2
1
2
tan 30°
y
x
213
6
cos 30°
x
r
6
413
sin 30°
y
r
213
413
30°,
60°
213
y
13
3
162 213.
x 6
tan 30°.sin 30°, cos 30°,
y
13
3
x,
tan 30°sin 30°, cos 30°,
60°
y
13
3
x.
rise
run
5
513
13
3
,
College Algebra & Trignometry—
10
6
10
10
10
x
y
30
30
2√3
(6, 2√3)
4√3
y
3
√3
x
Figure 5.23
Figure 5.24
cob19529_ch05_503-614.qxd 12/27/08 10:38 Page 532

5-31 Section 5.3 Trigonometry and the Coordinate Plane 533
both x and y are negative. If we consider the angle in QIII to be a positive rotation of
we can evaluate the trig functions using the values of x, y, and r
from any point on the terminal side, since these are fixed by the angle created and
are the same as those in QI except for their sign:
For any rotation and a point (x, y) on the terminal side, the distance r can be found
using and the six trig functions likewise evaluated. Note that evaluat-
ing them correctly depends on the quadrant of the terminal side, since this will dictate
the signs for x and y. Students are strongly encouraged to make these quadrant and sign
observations the first step in any solution process. In summary, we have
Trigonometric Functions of Any Angle
Given P(x, y) is any point on the terminal side of angle in standard position, with
the distance from the origin to (x, y). The six trigonometric
functions of are
EXAMPLE 2
Evaluating Trig Functions Given the Terminal Side is on
Given that P(x, y) is a point on the terminal side of angle in standard position,
find the value of and , if
a. The terminal side is in QII and coincident with the line ,
b. The terminal side is in QIV and coincident with the line .
Solution
a. Select any convenient point in QII that satisfies this equation. We select
since x is negative in QII, which gives and the point ( , 12).
Solving for r gives . The ratios are
b. In QIV we select since x is positive in QIV, giving and the point
(10, ). Solving for r gives . The ratios are
Now try Exercises 9 through 12
5
13
12
13
cos
x
r
10
26
sin
y
r
24
26
r 21102
2
1242
2
2624
y 24x 10
cos
x
r
5
13
sin
y
r
12
13
r 2152
2
1122
2
13
5y 12x 5
y
12
5
x
y
12
5
x
cos sin
y mx
y 0x 0y 0
cot
x
y
sec
r
x
csc
r
y
x 0
tan
y
x
cos
x
r
sin
y
r
1r 7 02r 2x
2
y
2
r 2x
2
y
2
13
3
13
2
1
2
tan 210°
y
x
213
6
cos 210°
x
r
6
413
sin 210°
y
r
213
413
30°
210° 1180° 30°2,
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:46 PM Page 533 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
534 CHAPTER 5 An Introduction to Trigonometric Functions 5-32
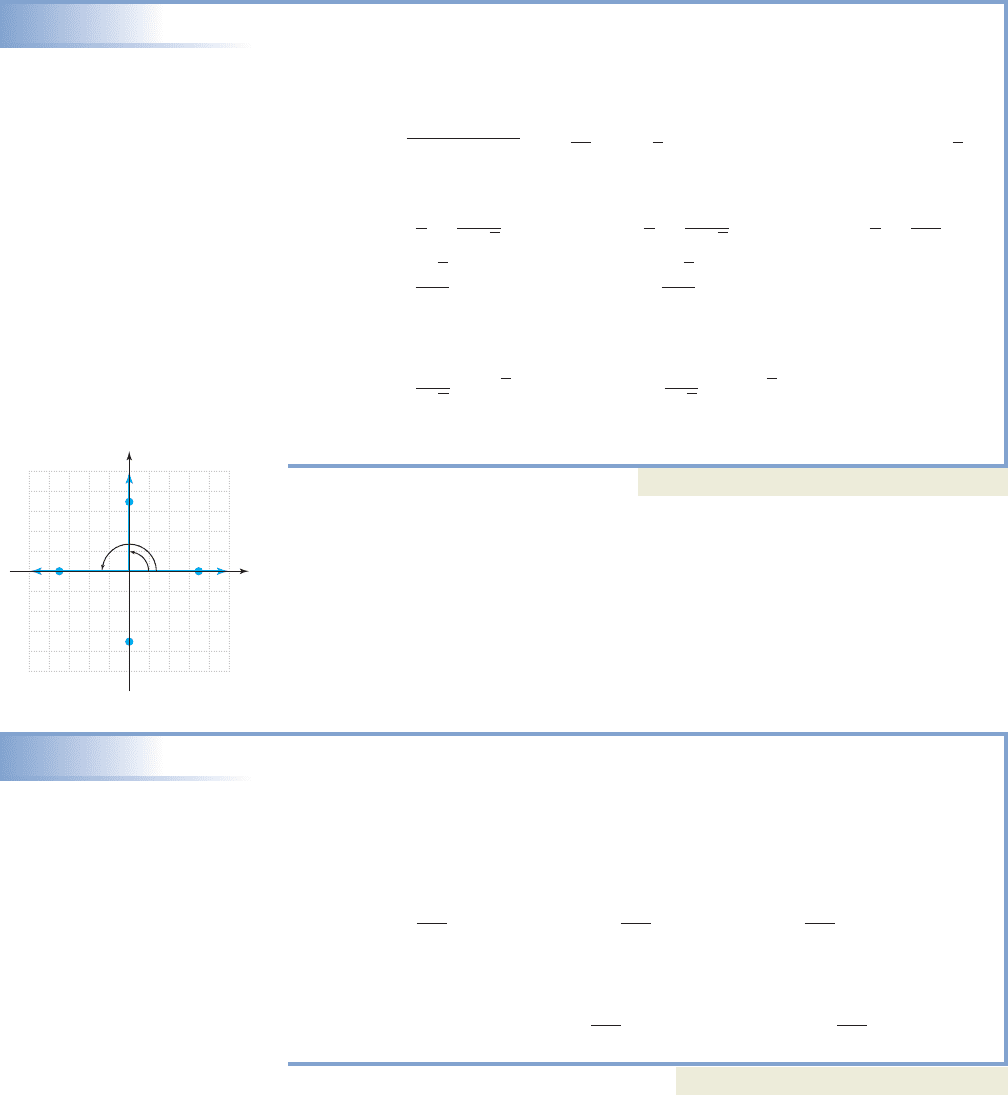
In Example 2, note the ratios are the same in QII and QIV except for their sign.
We will soon use this observation to great advantage.
EXAMPLE 3
Evaluating Trig Functions Given a Point P
Find the value of the six trigonometric functions given is on the terminal
side of angle in standard position.
Solution
For we have and so the terminal side is in QII. Solving for r
yields For and
we obtain
The remaining functions can be evaluated using reciprocals.
Note the connection between these results and the special values for
Now try Exercises 13 through 28
Now that we’ve defined the trig functions in terms of ratios involving x, y, and
r, the question arises as to their value at the quadrantal angles. For and ,
any point on the terminal side of the angle has an x-value of zero, meaning
, and are all undefined since is in the
denominator. Similarly, at and the y-value of any point on the terminal
side is zero, so , and are likewise undefined (see
Figure 5.25).
EXAMPLE 4
Evaluating the Trig Functions for , k an Integer
Evaluate the six trig functions for .
Solution
Here, is the quadrantal angle whose terminal side separates QIII and QIV. Since
the evaluation is independent of the point chosen on this side, we choose (0, )
for convenience, giving For and we obtain
The remaining ratios can be evaluated using reciprocals.
Now try Exercises 29 and 30
csc 1
sec
1
0
1undefined2
cot
0
1
0
sin
1
1
1
cos
0
1
0
tan
1
0
1undefined2
r 1x 0, y 1,r 1.
1
270°
90k
csc 360°cot 180°, csc 180°, cot 360°
360°,180°
x 0sec 270°tan 90°, sec 90°, tan 270°
270°90°
45°.
cot 1sec
2
12
12csc
2
12
12
1
12
2
12
2
tan
y
x
5
5
cos
x
r
5
512
sin
y
r
5
512
r 512,x 5, y 5,r 2152
2
152
2
150 512.
y 7 0x 6 0P15, 52
P15, 52
90
180
(0, b)
(0, b)
(a, 0)(a, 0)
y
x
Figure 5.25
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:46 PM Page 534 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
5-33 Section 5.3 Trigonometry and the Coordinate Plane 535
Results for the quadrantal angles are summarized in Table 5.3.
0 1 0 undefined 1 undefined
1 0 undefined 1 undefined 0
0 0 undefined undefined
0 undefined undefined 011270° S 10, 12
11180° S 11, 02
90° S 10, 12
0° S 11, 02
cot
x
y
sec
r
x
csc
r
y
tan
y
x
cos
x
r
sin
y
r
Table 5.3
B. Reference Angles and the Trig Functions of Any Angle
By defining a reference angle we can evaluate the trigonometric functions given
a point (x, y) on the terminal side of an
y angle.
Reference Angles
For any angle in standard position, the acute angle formed by the terminal side
and the x-axis is called the reference angle for .
r
r
,
55
5
5
r
(x, y)
x
y
360 450
r
360
55
5
5
r
(x, y)
x
y
270 360
r
360
55
5
5
r
x
y
(x, y)
180 270
r
180
y
55
5
5
r
x
(x, y)
90 180
r
180
Figure 5.26
Figure 5.27 Figure 5.28
Figure 5.29
EXAMPLE 5
Finding Reference Angles
Determine the reference angle for
a. b. c. d.
Solution
Begin by mentally visualizing each angle and the quadrant where it terminates.
a. is a QIV angle: c. is a QIII angle:
b. is a QII angle: d. is a QI angle:
Now try Exercises 31 through 42
The reference angles from Examples 5(a) and 5(b) were special angles,
which means we automatically know the absolute value of the trig ratios using
. The best way to remember the signs of the trig functions is to keep in mind
r
r
425° 360° 65°
r
180° 150° 30°
425°150°
r
180° 121° 59°
r
360° 315° 45°
121°315°
425°121°150°315°
College Algebra & Trignometry—
A. You’ve just learned how
to define the trigonometric
functions using the coordinates
of a point in QI
Several examples of the reference angle concept are illustrated in Figures 5.26 through
5.29 for in degrees, . 7 0
cob19529_ch05_503-614.qxd 12/27/08 10:39 Page 535
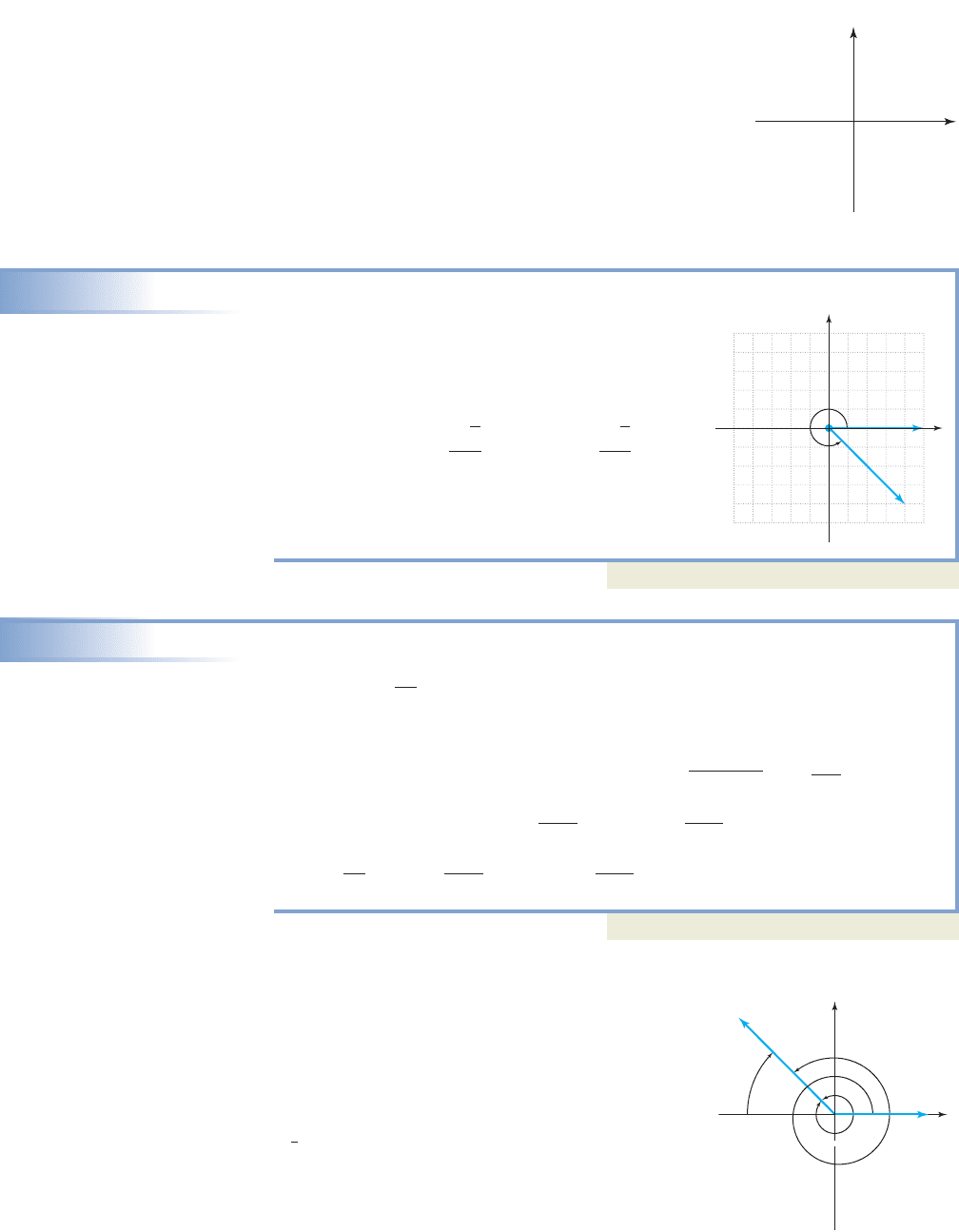
536 CHAPTER 5 An Introduction to Trigonometric Functions 5-34
that sine is associated with y, cosine with x, and
tangent with both x and y (r is always positive). In
addition, there are several mnemonic devices (memory
tools) to assist you. One is to use the first letter of the
function that is positive in each quadrant and create a
catchy acronym. For instance ASTC All Students
Take Classes (see Figure 5.30). Note that a trig func-
tion and its reciprocal function will always have the
same sign.
EXAMPLE 6
Evaluating Trig Functions Using
Use a reference angle to evaluate and
for .
Solution
The terminal side is in QIV where x is positive and
y is negative. With , we have:
Now try Exercises 43 through 54
EXAMPLE 7
Finding Function Values Using a Quadrant and Sign Analysis
Given and , find the value of the other ratios.
Solution
Always begin with a quadrant and sign analysis: is positive in QI and QII, while
is negative in QII and QIII. Both conditions are satisfied in QII only. For
and , the Pythagorean theorem shows
With in QII this gives and . The reciprocal values are
, , and .
Now try Exercises 55 through 62
In our everyday experience, there are many
actions and activities where angles greater than or
equal to are applied. Some common instances
are a professional basketball player who “does a
three-sixty” ( ) while going to the hoop, a diver
who completes a “two-and-a-half” ( ) off the high
board, and a skater who executes a perfect triple axel
( turns or ). As these examples suggest, angles
greater than must still terminate on a quadrantal
axis, or in one of the four quadrants, allowing a refer-
ence angle to be found and the functions to be evalu-
ated for any angle regardless of size. Figure 5.31
illustrates that , and are all coterminal, with each
having a reference angle of 45°.
495° 135°, 225°
360°
1260°3
1
2
900°
360°
360°
cot
12
5
sec
13
12
csc
13
5
tan
5
12
cos
12
13
x 213
2
5
2
1144 12.y 5
r 13cos
sin
cos 6 0sin
5
13
tan 315° 1
sin 315°
12
2
cos 315°
12
2
r
45°
315°tan
sin , cos ,
r
S
Figure 5.30
Quadrant II
Sine
is positive
Tangent
is positive
Quadrant III
Quadrant I
All
are positive
Cosine
is positive
Quadrant IV
495
y
x
135
45
225
Figure 5.31
College Algebra & Trignometry—
8
8
315
x
y
r
45
cob19529_ch05_503-614.qxd 11/11/08 1:46 PM Page 536 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:
5-35 Section 5.3 Trigonometry and the Coordinate Plane 537
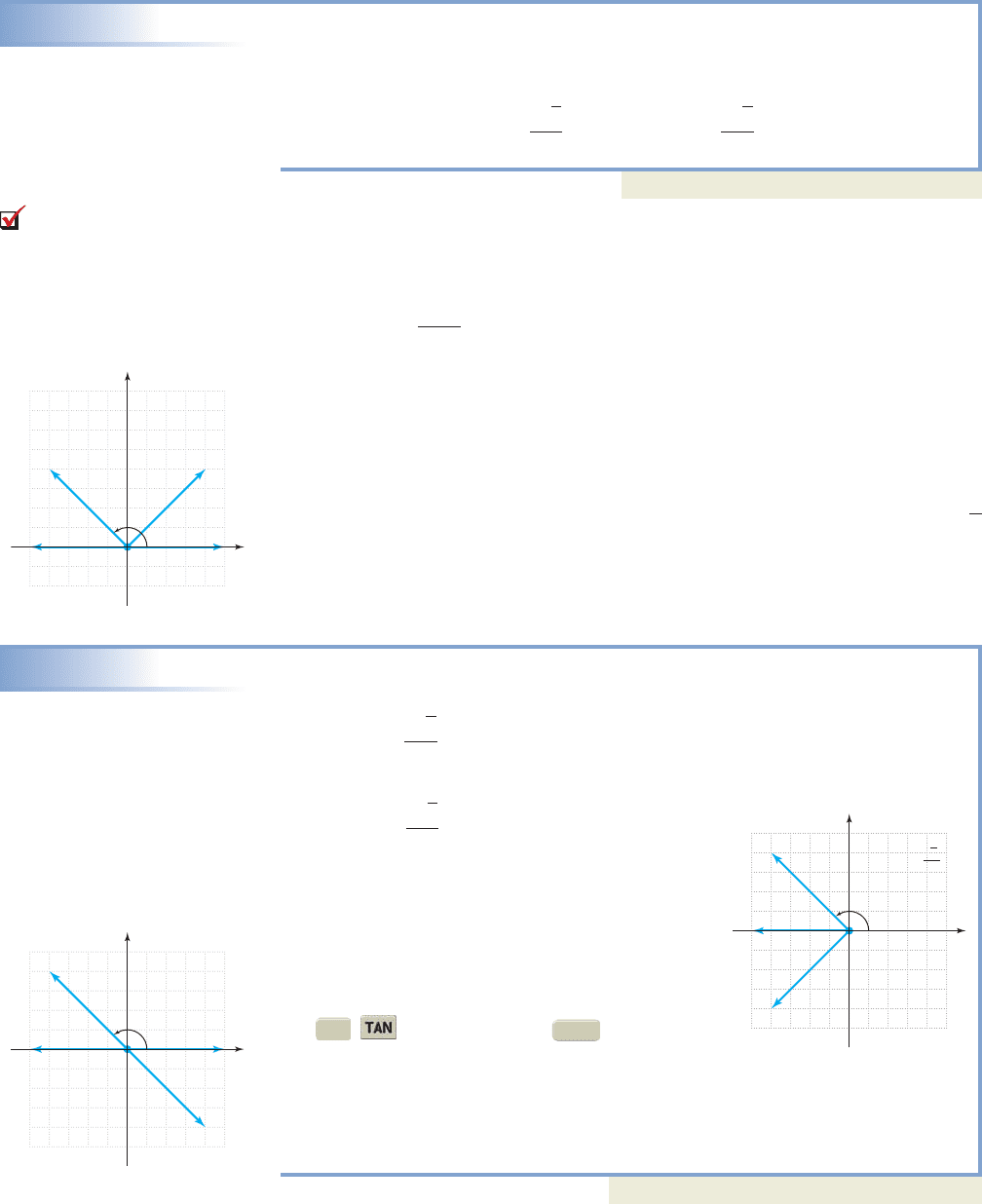
EXAMPLE 8
Evaluating Trig Functions of Any Angle
Evaluate , and .
Solution
The angles are coterminal and terminate in QII, where and . With
we have , and .
Now try Exercises 63 through 74
Since is one full rotation, all angles will be coterminal for any
integer k. For angles with a very large magnitude, we can find the quadrant of the ter-
minal side by subtracting as many integer multiples of as needed from the angle.
For and . This angle is in QII with
. See Exercises 75 through 90.
C. Applications of the Trig Functions of Any Angle
One of the most basic uses of coterminal angles is determining all values of that
satisfy a stated relationship. For example, by now you are aware that if
(positive one-half), then or (see Figure 5.32). But this is also true
for all angles coterminal with these two, and we would write the solutions as
and for all integers k.
EXAMPLE 9
Finding All Angles that Satisfy a Given Equation
Find all angles satisfying the relationship given. Answer in degrees.
a. b.
Solution
a. Cosine is negative in QII and QIII. Recognizing
, we reason and two
solutions are from QII and
from QIII. For all values of satisfying the
relationship, we have and
. See Figure 5.33.
b. Tangent is negative in QII and QIV. For
we find using a calculator:
() shows
, so .
Two solutions are from QII, and in QIV
. The result is and
. Note these can be combined into the single statement
. See Figure 5.34.
Now try Exercises 93 through 100
We close this section with an additional application of the concepts related to
trigonometric functions of any angle.
126° 180°k
306° 360°k
126° 360°k 360° 54° 306°
180° 54° 126°
r
54°tan
1
11.37642 54
ENTER
1.3764
tan
1
2nd
r
1.3764
225° 360°k
135° 360°k
225° 135°
r
45°cos 45°
12
2
tan 1.3764
cos
12
2
150° 360°k 30° 360°k
150° 30°
sin
1
2
r
72°
1908 360152 108° 1908°,
1908
360
5.3
360°
360°k360°
tan 495° 1sin 135°
12
2
, cos 1225°2
12
2
r
45°
y 7 0x 6 0
tan 495°sin 135°, cos 1225°2
B. You’ve just learned how
to use reference angles to
evaluate the trig functions for
any angle
150
30
r
30
8
5
x
y
Figure 5.32
cos
√2
2
135
r
45
r
45
8
x
y
Figure 5.33
126
tan 1.3764
r
54
r
54
8
5
x
y
Figure 5.34
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 11/11/08 1:46 PM Page 537 epg HD 049:Desktop Folder:Coburn_do_t del-ch05:

538 CHAPTER 5 An Introduction to Trigonometric Functions 5-36
EXAMPLE 10
Applications of Coterminal Angles: Location on Radar
A radar operator calls the captain over to her screen
saying, “Sir, we have an unidentified aircraft
heading ( east of due north or a standard
rotation). I think it’s a UFO.” The captain asks,
“What makes you think so?” To which the sailor
replies, “Because it’s at 5000 ft and not moving!”
Name all angles for which the UFO causes a “blip”
to occur on the radar screen.
Solution
Since radar typically sweeps out a angle, a blip
will occur on the screen for all angles
, where k is an integer.
Now try Exercises 101 through 106
70° 360°k
360°
70°
20°20°
70
Blip!
x
y
C. You’ve just learned how
to solve applications using
the trig functions of any angle
5.3 EXERCISES
Fill in each blank with the appropriate word or phrase.
Carefully reread the section if needed.
1. An angle is in standard position if its vertex is at
the and the initial side is along the
.
2. A(n) angle is one where the
side is coincident with one of the coordinate axes.
3. Angles formed by a counterclockwise rotation are
angles. Angles formed by a
rotation are negative angles.
4. For any angle , its reference angle is the
positive angle formed by the
side and the nearest x-axis.
5. Discuss the similarities and differences between
the trigonometry of right triangles and the
trigonometry of any angle.
6. Let T(x) represent any one of the six basic trig
functions. Explain why the equation will
always have exactly two solutions in [0, ) if x is
not a quadrantal angle.
2
T1x2 k
r
CONCEPTS AND VOCABULARY
7. Draw a 30-60-90 triangle with the angle
at the origin and the short side along the positive
x-axis. Determine the slope and equation of the
line coincident with the hypotenuse, then pick
any point on this line and evaluate
, and . Comment on what you
notice.
8. Draw a 45-45-90 triangle with a angle at the
origin and one side along the positive x-axis.
Determine the slope and equation of the line
coincident with the hypotenuse, then pick any
45°
tan 60°cos 60°
sin 60°,
60°
point on this line and evaluate , and
. Comment on what you notice.
Graph each linear equation and state the quadrants
it traverses. Then pick one point on the line from each
quadrant and evaluate the functions sin , cos and
tan using these points.
9. 10.
11. 12. y
13
2
xy
13
3
x
y
5
12
xy
3
4
x
tan 45
sin 45°, cos 45°
DEVELOPING YOUR SKILLS
College Algebra & Trignometry—
cob19529_ch05_503-614.qxd 12/27/08 10:39 Page 538

5-37 Section 5.3 Trigonometry and the Coordinate Plane 539
Find the value of the six trigonometric functions given
P(x, y) is on the terminal side of angle , with in
standard position.
13. (8, 15) 14. (7, 24)
15. ( , 21) 16. ()
17. (7.5, ) 18. (9, )
19. () 20. ()
21. (2, 8) 22. (6, )
23. ()24. (6.75, 9)
25. 26.
27. 28.
29. Evaluate the six trig functions in terms of x, y, and
r for
30. Evaluate the six trig functions in terms of x, y, and
r for
Name the reference angle for the angle given.
31. 32.
33. 34.
35. 36.
37. 38.
39. 40.
41. 42.
State the quadrant of the terminal side of using the
information given.
43.
44.
45.
46.
Find the exact value of
,
, and using
reference angles.
47. 48.
49. 50.
51. 52.
53. 54.
For the information given, find the values of x, y, and r.
Clearly indicate the quadrant of the terminal side of ,
then state the values of the six trig functions of .
210° 150°
315° 240°
120° 45°
390° 330°
tan cos sin
sec 7 0, tan 7 0
tan 6 0, sin 7 0
cos 6 0, tan 6 0
sin 7 0, cos 6 0
,
328.2° 168.4°
750° 500°
179° 112°
240° 45°
315° 135°
210° 120°
r
180°.
90°.
a
13
5
,
22
25
ba
1
4
,
15
2
b
a
3
4
,
7
16
ba
5
9
,
2
3
b
3.75, 2.5
15
6, 613
413, 4
97.5
3, 120
55. and
56. and
57. and
58. and
59. and
60. and
61. and
62. and
Find two positive and two negative angles that are
coterminal with the angle given. Answers will vary.
63. 64.
65. 66.
67. 68.
69. 70.
Evaluate in exact form as indicated.
71.
72.
73.
74.
Find the exact value of , , and using
reference angles.
75. 76.
77. 78.
79. 80.
81. 82.
For each exercise, state the quadrant of the terminal
side and the sign of the function in that quadrant. Then
evaluate the expression using a calculator. Round to
four decimal places.
83. 84.
85. 86.
87. 88.
89. 90. sin 772°cos 805°
tan 995°csc 681°
sec1621°2tan1419°2
cos 528°sin 719°
3270° 1230°
495° 570°
930° 840°
480° 600°
tan cos sin
sin 210°, cos 570°, tan1150°2
sin130°2, cos1390°2, tan 690°
sin 225°, cos 585°, tan1495°2
sin 120°, cos1240°2, tan 480°
215°107°
175°225°
22.8°87.5°
12°52°
sin 6 0cos
5
12
sec 6 0sin
7
8
cos 7 0csc 2
cos 7 0csc 3
cot 6 0sin
20
29
tan 7 0csc
37
35
cos 7 0tan
12
5
sin 6 0cos
4
5
College Algebra & Trignometry—
cob19529_ch05_532-541.qxd 12/29/08 4:50 PM Page 539 epg HD 049:Desktop Folder:Satya 29/12/08:Coburn_do_t del-ch05:MHDQ092-5.3:
