CIMA - C3 Fundamentals Of Business Mathematics

Подождите немного. Документ загружается.

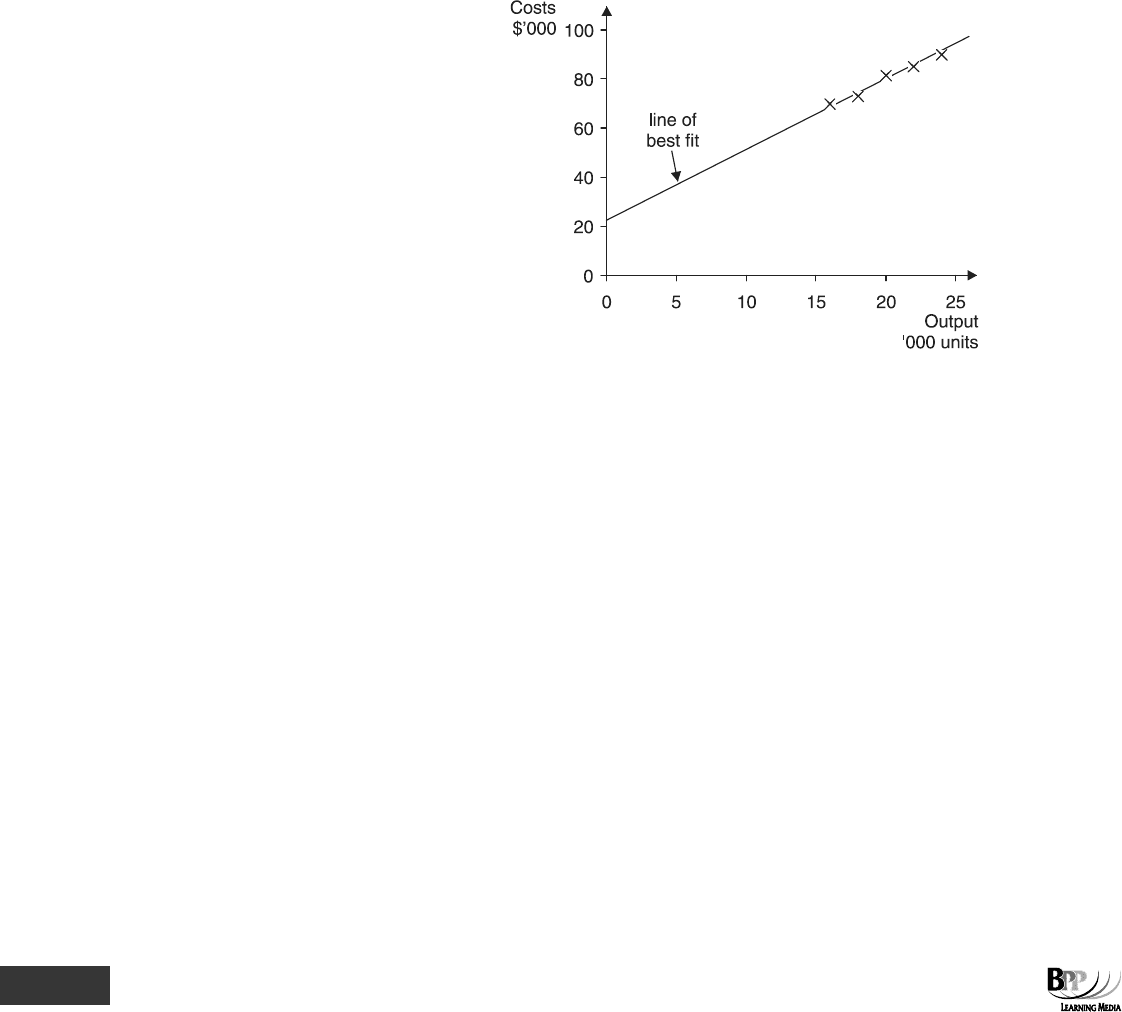
270 10: Correlation and linear regression ⏐ Part E Inter-relationships between variables

5.1 Example: The scattergraph method

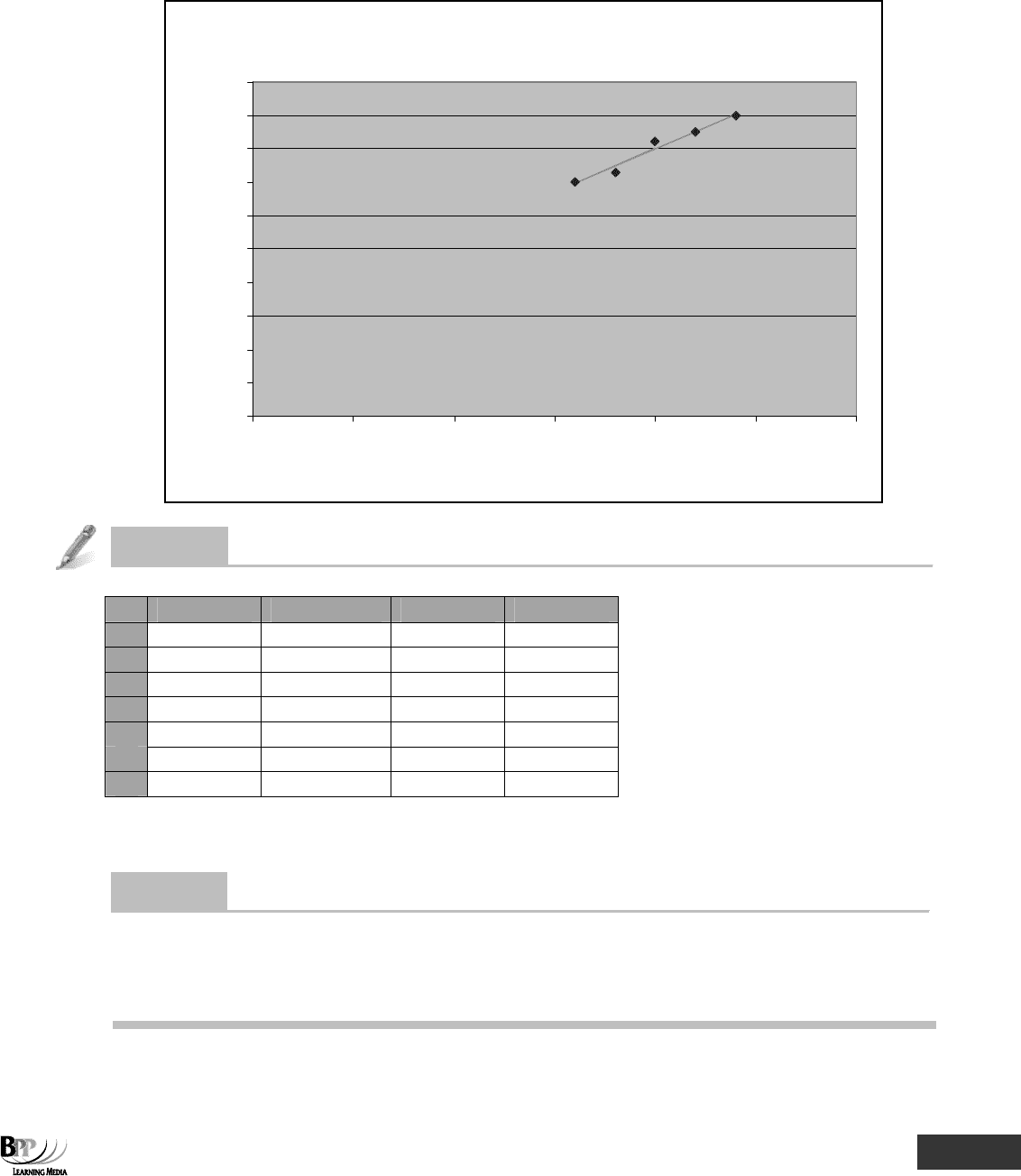
Suppose we have the following pairs of data about output and costs.

Month

Output Costs

'000 units $'000

1 20 82

2 16 70

3 24 90

4 22 85

5 18 73

(a) These pairs of data can be plotted on a scattergraph (the horizontal axis representing the independent

variable and the vertical axis the dependent) and a line of best fit might be judged as the one shown below.

It is drawn to pass through the middle of the data points, thereby having as many data points below the line

as above it.

(b) A

formula for the line of best fit can be found. In our example, suppose that we read the following data

from the graph.

(i) When X = 0, Y = 22,000. This must be the value of

a in the formula Y = a + bX.

(ii) When X = 20,000, Y = 82,000. Since Y = a + bX, and a = 22,000, 82,000 = 22,000 + (b × 20,000)

b × 20,000 = 60,000

b = 3

5.2 Forecasting and scattergraphs

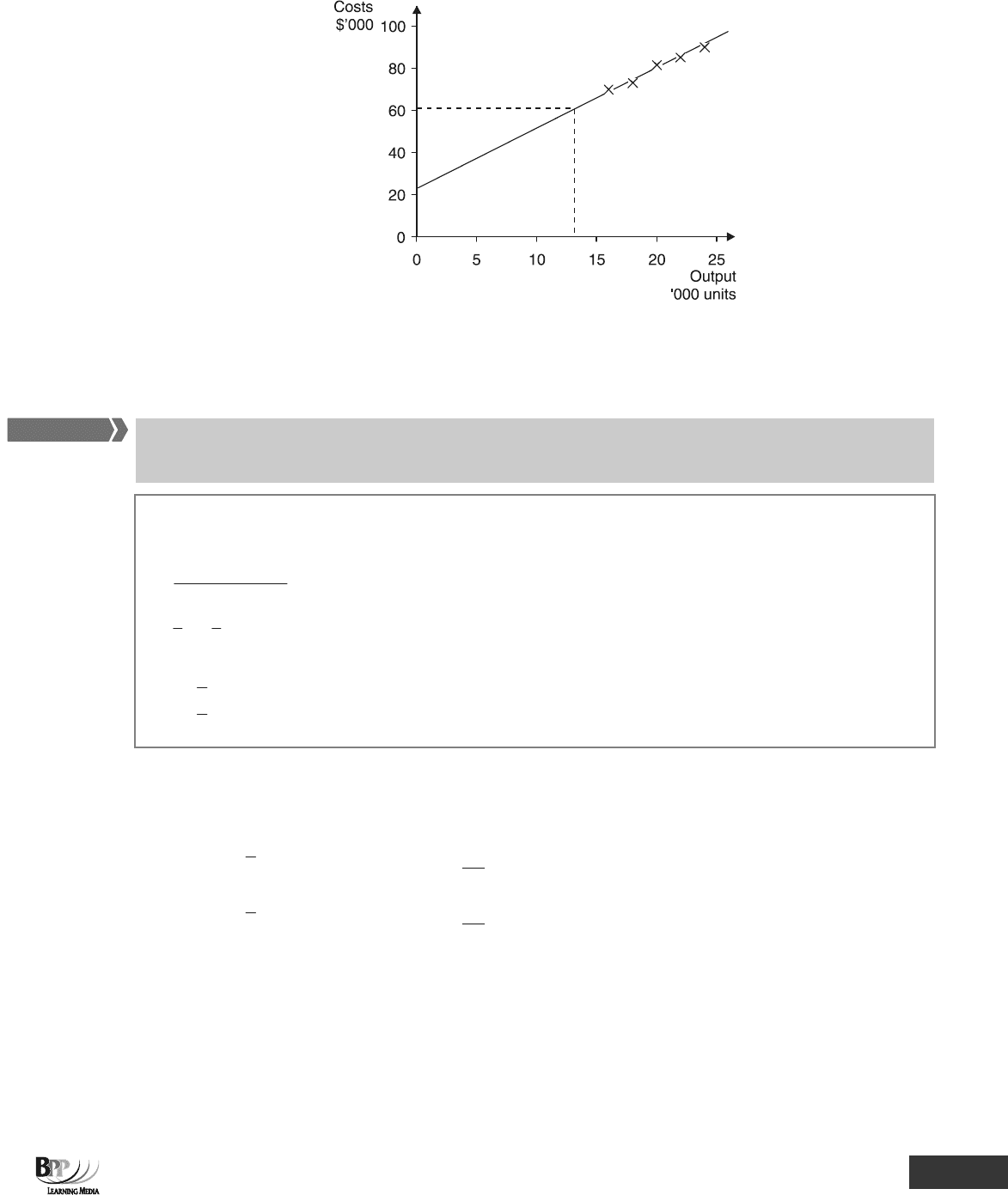
If the company to which the data in Paragraph 5.1 relates wanted to predict costs at a certain level of output (say

13,000 units), the value of 13,000 could be substituted into the equation Y = 22,000 + 3X and an estimate of costs

made.

If X = 13, Y = 22,000 + (3 × 13,000)

∴ Y = $61,000

Predictions can be made directly from the scattergraph, but this will usually be less accurate.

Part E Inter-relationships between variables ⏐ 10: Correlation and linear regression 271

The prediction of the cost of producing 13,000 units from the scattergraph is $61,000.

6 Linear regression analysis

Linear regression analysis (the least squares method) is one technique for estimating a line of best fit. Once an

equation for a line of best fit has been determined, forecasts can be made.

The least squares method of linear regression analysis involves using the following formulae for a and b in Y = a

+ bX.

b =

nXY XY

nX (X)

∑−∑∑

∑−∑

a =

– b

Where n is the number of pairs of data

is the mean X value of all the pairs of data

is the mean Y value of all the pairs of data

6.1 Some helpful hints

(a) The value of b must be calculated first as it is needed to calculate a.

(b)

is the mean of the X values =

Y is the mean of the Y values =

(d) Set your workings out in a table to find the figures to put into the formulae.

Assessment

formula

T F

RWAR

272 10: Correlation and linear regression ⏐ Part E Inter-relationships between variables

6.2 Example: Linear regression analysis

(a) Given that there is a fairly high degree of correlation between the output and the costs detailed in Paragraph

5.1 (so that a linear relationship can be assumed), calculate an equation to determine the expected level of

costs, for any given volume of output, using the least squares method.

(b) Prepare a budget for total costs if output is 22,000 units.

coefficient.

Solution

(a) Workings

1,640

400

6,724

1,120

256

4,900

2,160

576

8,100

1,870

484

7,225

1,314

324

5,329

∑X =

100

∑Y =

400

∑XY =

8,104

∑X

2,040

∑Y

32,278

n = 5 (There are five pairs of data for x and y values)

b =

()

XXn

YXXYn

∑−∑

∑∑−∑

1002,040)(5

400)(1008,104)(5

−×

×−×

10,00010,200

40,00040,520

−

200

520

= 2.6

a =

– b

400

– 2.6 ×

⎟

⎠

⎞

⎜

⎝

⎛

100

= 28

Y = 28 + 2.6X

Where Y = total cost, in thousands of pounds

X = output, in thousands of units

Compare this equation to that determined in Paragraph 5.1.

Note that the fixed costs are $28,000 (when X = 0 costs are $28,000) and the variable cost per unit is $2.60.

(b) If the output is 22,000 units, we would expect costs to be

28 + (2.6 × 22) = 85.2 = $85,200.

)400278,325(200

520

−××

390,1200

520

3.527

520

= + 0.986

In an assessment, you might be required to use the linear regression analysis technique to calculate the values of a

and b in the equation y = a + bx. This type of task is ideally tested by objective test questions.

Assessment

focus point

Part E Inter-relationships between variables ⏐ 10: Correlation and linear regression 273

Question

Linear regression analysis

If Σx = 79, Σy = 1,466, Σx

= 1,083, Σy

= 363,076, Σxy = 19,736 and n = 6, then the value of b, the gradient, to two

decimal places, is:

A 10.12

B 111.03

C 13.62

D –8.53

Answe

r =

(6× 19,736)-(79 ×1,466)

(6 ×1,083)- 79

118,416 -115,814

6,498 - 6,241

2,602

257

= 10.12

Question

Forecasting

In a forecasting model based on y = a + bx, the intercept is $262. If the value of y is $503 and x is 23, then the value

of the gradient, to two decimal places, is:

A –20.96

B –10.48

C 10.48

D 20.96

Answe

C y = a + bx

503 = 262 + (b × 23)

241 = b × 23

b = 10.48

7 Using spreadsheets

Excel has a built-in formula =FORECAST for the calculation of the regression (least squares) line.

7.1 The scattergraph

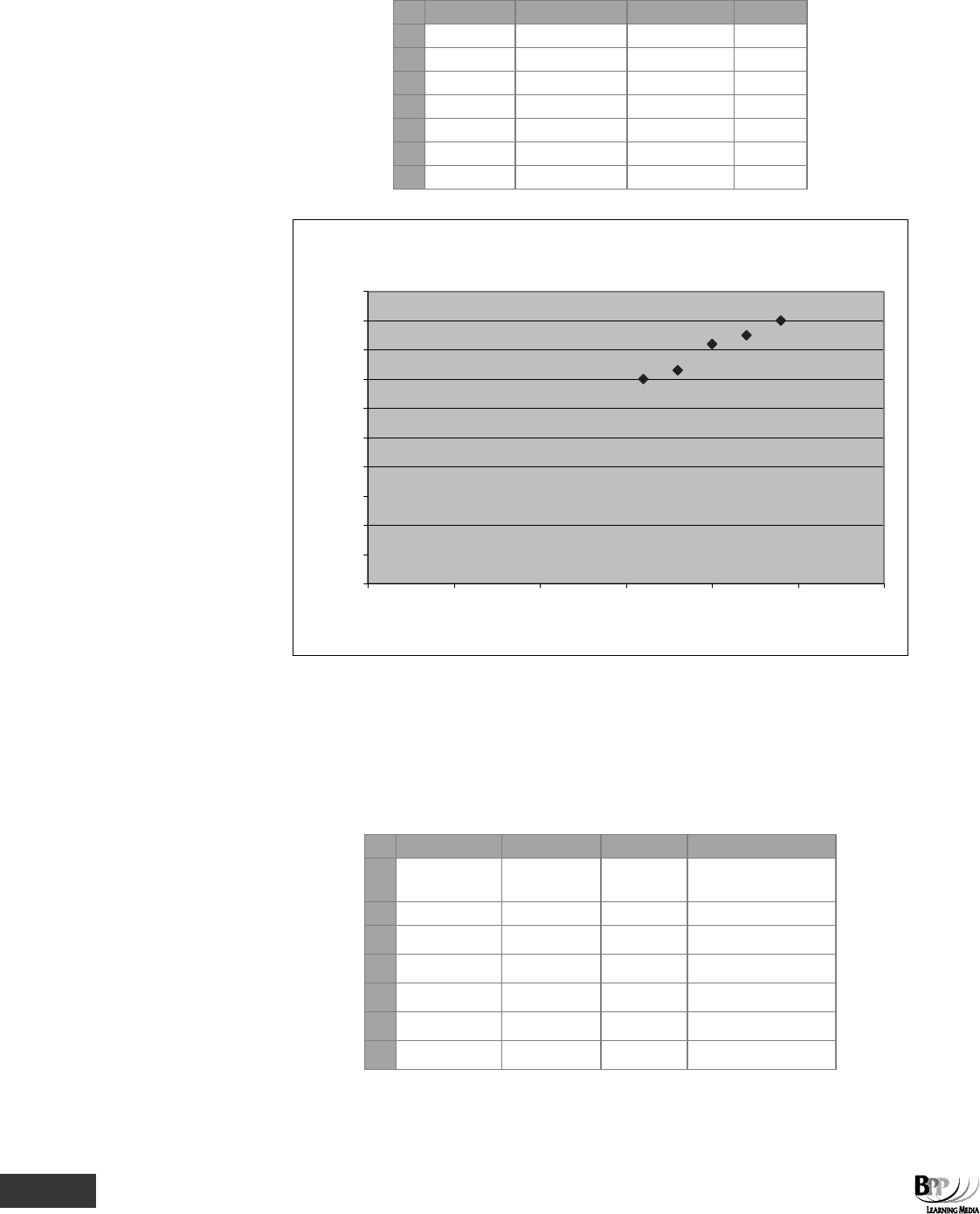
We have already seen how to use the chart wizard to produce charts and graphs in Excel. One of the chart options

available is the scattergraph. Using the data from paragraph 5.1, the following spreadsheet and chart can be

produced.

T F

RWAR

274 10: Correlation and linear regression ⏐ Part E Inter-relationships between variables

A B C

1 Month Output Costs

2 '000 units $'000

3 1 20 82

4 2 16 70

5 3 24 90

6 4 22 85

7 5 18 73

A scattergraph

100

0 5 10 15 20 25 30

Ouput '000 units

Costs $'000

7.2 The FORECAST function

We can use the FORECAST function to plot the regression line. The formula

=FORECAST(B3,$C$3:$C$7,$B$3:$B$7) is entered in cell D3 and copied down the column. Note how

absolute cell

references

are used to ensure that each observation is compared with the entire range.

A B C D

1 Month Output Costs Regression line

2 000 units $'000

3 1 20 82

4 2 16 70

5 3 24 90

6 4 22 85

7 5 18 73

Part E Inter-relationships between variables ⏐ 10: Correlation and linear regression 275

To plot this forecast data on the chart, select the range D3:D7, click copy then click on the chart and click paste. In

order to create a joined up line as shown in the chart below, right click and format the data series to set the line to

'automatic' and the marker to 'none'.

A scattergraph

100

0 5 10 15 20 25 30

Ouput '000 units

Costs $'000

Question

Forecast function

A B C D

1 Output Costs

2 Units $

3 280 46,500

4 350 49,100

5 200 36,700

6 160 32,000

7 240 44,500

What formula should be entered into cell C3 to forecast the costs for a given level of output if the formula is to be

copied into cells C4 to C7?

Answe

The FORECAST

function should be used with absolute cell references for the cells marking the range of data to be

used.

=FORECAST(A3,$B$3:$B$7,$A$3:$A$7)

276 10: Correlation and linear regression ⏐ Part E Inter-relationships between variables

Chapter Roundup

• When the value of one variable is related to the value of another, they are said to be correlated.

• Two variables might be perfectly correlated, partly correlated or uncorrelated. Correlation can be positive or

negative.

• The degree of correlation between two variables is measured by the Pearson's correlation coefficient, r. The

nearer r is to +1 or –1, the stronger the relationship.

• The coefficient of determination, r

, measures the proportion of the total variation in the value of one variable that

can be explained by variations in the value of the other variable.

• Spearman's rank correlation coefficient is used when data is given in terms of order or rank, rather than actual

values.

• The scattergraph method involves the use of judgement to draw what seems to be a line of best fit through plotted

data.

• Linear regression analysis (the least squares method) is one technique for estimating a line of best fit. Once an

equation for a line of best fit has been determined, forecasts can be made.

• Excel has a built-in formula =FORECAST for the calculation of the regression (least squares) line.

Part E Inter-relationships between variables ⏐ 10: Correlation and linear regression 277

Quick Quiz

1 correlation means that low values of one variable are associated with low values of the

other, and high values of one variable are associated with high values of the other.

2 correlation means that low values of one variable are associated with high values of the

other, and high values of one variable with low values of the other.

3 • Perfect positive correlation, r =

• Perfect negative correlation, r =

• No correlation, r =

The correlation coefficient, r, must always fall within the range to

4 If the correlation coefficient of a set of data is 0.95, what is the coefficient of determination?

5 If Y = a + bX, it is best to use the regression of Y upon X where X is the dependent variable and Y is the

independent variable.

True

False F

6 Which Excel function can be used to calculate a future value by using existing values?

7 If Σx = 30, Σy = 62, Σx

= 238, Σy

= 1,014, Σxy = 485, n = 4

What is the correlation coefficient? (to 2 decimal places)

278 10: Correlation and linear regression ⏐ Part E Inter-relationships between variables

Answers to Quick Quiz

1 Positive correlation

2 Negative correlation

3 • r = +1

• r = –1

• r = 0

The correlation coefficient, r, must always fall within the range –1 to +1.

4 Correlation coefficient = r = 0.95

Coefficient of determination = r

= 0.95

= 0.9025 or 90.25%

This tells us that over 90% of the variations in the dependent variable (Y) can be explained by variations in the

independent variable, X.

5 False. When using the regression of Y upon X, X is the independent variable and Y is the dependent variable (the

value of Y will depend upon the value of X).

6 =FORECAST

7 r =

])y(yn][)x(xn[

yxxyn

2222

Σ−ΣΣ−Σ

ΣΣ−Σ

]621,014) x [(4 x ]30238) x [(4

62) x (30485) x (4

−−

−

212 x 52

1,860 - 1,940

104.995

= 0.76

Now try the questions below from the Exam Question Bank

Question numbers Pages

79-88 344-347

279

Part F

Forecasting