Чорний О.П., Луговой А.В. и др. Моделювання електромеханічних систем

Подождите немного. Документ загружается.

(

)

(

)

(

)

=−⋅

(12.20)

Тепер ми можемо записати (12.14) у розкритому виді:

∆w

n() () ( )

=− ⋅ ⋅

−

ηδ

y (12.21)

Іноді для надання процесу корекції вагових коефіцієнтів

деякої інерційності, що згладжує різкі скачки при переміщенні

по поверхні цільової функції, (12.21) доповнюється значенням

зміни вагових коефіцієнтів на попередній ітерації

(

)

()

(

)

()

(

)

(

)

(

)

∆∆wt wt y

=−⋅⋅ −+−⋅ ⋅

−

ηµ µδ11

(12.22)

де

µ - коефіцієнт інерційності, t - номер поточної ітерації.

Таким чином, повний алгоритм навчання НМ за

допомогою процедури зворотного поширення будується так:

1. Подати на входи мережі один із можливих наборів

вихідних сигналів і в режимі звичайного функціонування НМ,

коли сигнали поширюються від входів до виходів, розрахувати

значення вихівних. Нагадаємо, що

(

)

(

)

(

)

syw

=⋅

−

∑

(12.23)

де

- число нейронів у шарі n

−

1 з обліком нейрона з

постійним вихідним станом

1, що задає зсув;

(

)

(

)

−

-й вхід нейрона i

шару n .

(

)

(

)

(

)

yfs

= , де

(

)

(

)

- сигмоїд (12.24)

(

)

= I

, (12.25)

де

- -а компонента вектора вхідного способу. I

2. Розрахувати

(

)

для вихідного шару по формулі

(12.20).

Розрахувати по формулі (12.21) або (12.22) зміни ваг

шару

(

)

∆w

312

3. Розрахувати по формулах (12.19) і (12.21) (або (12.19) і

(12.22)) відповідно

(

)

(

)

∆

для всіх інших шарів,

=−11,... .

4. Скорегувати усі ваги в НМ

(

)

()

(

)

()

(

)

()

wt wt wt

=−+1 ∆ (12.26)

5. Якщо помилка мережі істотна, перейти на крок 1. У

противному випадку - кінець.

Мережі на кроку 1 поперемінно у випадковому порядку

пред'являються всі тренувальні способи, щоб мережа, образно

говорячи, не забувала одні в міру запам'ятовування інших.

Алгоритм ілюструється рис.12.5.

З виразу (12.21) випливає, що коли вихідне значення

прагне до нуля, ефективність навчання помітно

знижується. При двійкових вхідних векторах у середньому

половина вагових коефіцієнтів не буде коректуватися [3], тому

область можливих значень виходів нейронів [0,1] бажано

зрушити в межі [-0. 5,+0.5], що досягається простими

модифікаціями логістичних функцій. Наприклад, сигмоїд із

експонентою набере вигляду:

(

)

−1

() .=− +

−⋅

(12.27)

Тепер торкнемося питання ємності НМ, тобто числа способів,

запропонованих на її входи, що вона здатна навчитися

розпізнавати.

313

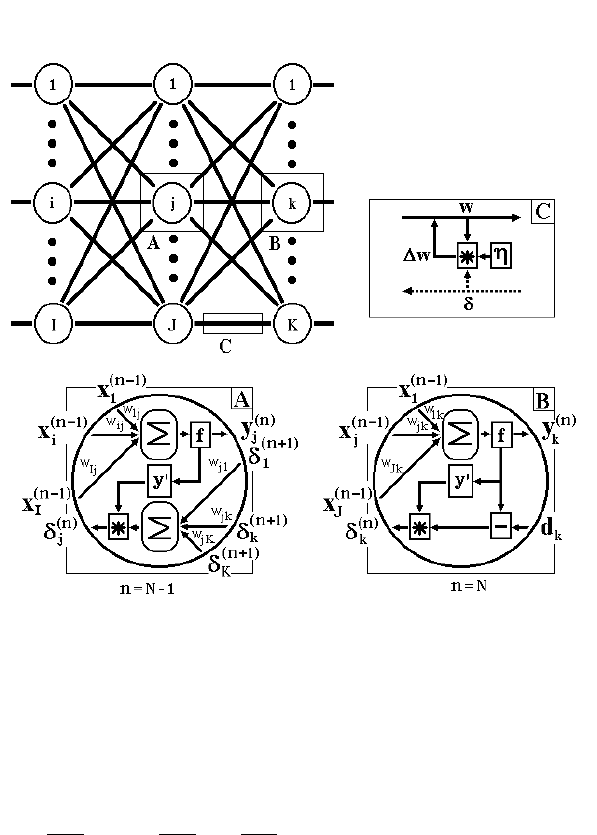
схований

шар

вихід

вхід

Рис.12.5. Діаграма сигналів у мережі при навчанні по

алгоритму зворотного поширення

Для мереж із числом шарів більше двох, він залишається

відкритим.

Для НМ із двома шарами, тобто вихідним і одним

схованим шаром, детерміністська ємність мережі

оцінюється так:

⎛

⎝

⎜

⎞

⎠

⎟

log

, (12.28)

де

- число вагових коефіцієнтів, що корегуються, -

число нейронів у вихідному шарі.

314

Слід зазначити, що даний вираз отримано з врахуванням

деяких обмежень. По-перше, число входів N

і нейронів у

схованому шарі

повинно задовольняти нерівності

. По-друге,

NNN

> 1000 . Однак вищенаведена

оцінка виконувалася для мереж з активаційними функціями

нейронів у вигляді порога, а ємність мереж із гладкими

активаційними функціями, наприклад - (12.27), звичайно

більше. Крім того, присутність в назві ємності прикметника

"детерміністський" означає, що отримана оцінка ємності

підходить абсолютно для всіх можливих вхідних сигналів, що

можуть бути подані

входами. У дійсності розподілу

вхідних сигналів, як правило, присутня регулярність, що

дозволяє НМ проводити узагальнення і, таким чином,

збільшувати реальну ємність. Так як розподіл сигналів, у

загальному випадку, заздалегідь не відомий, ми можемо

говорити про таку ємність тільки приблизно, але звичайно

вона рази в два перевищує ємність детерміністську.

У продовження

розмови про ємність НМ логічно

торкнути питання про необхідну потужність вихідного шару

мережі, що виконує остаточну класифікацію сигналів. Справа

в тому, що для поділу множини вхідних сигналів, наприклад,

по двох класах досить усього одного виходу. При цьому

кожний логічний рівень - "1" і "0" - буде позначати окремий

клас. На двох виходах можна закодувати уже

4 класи і так

далі. Однак результати роботи мережі, організованої таким

чином, можна сказати - "під зав'язку", - не дуже надійні. Для

підвищення вірогідності класифікації бажано ввести

надмірність шляхом виділення кожному класу одного нейрона

у вихідному шарі або, що ще краще, кількох, кожний із який

навчається визначати приналежність сигналу до класу зі

своїм

ступенем вірогідності, наприклад: високою, середньої і

низкою. Такі НМ дозволяють проводити класифікацію вхідних

сигналів, об'єднаних у нечіткі (розмиті або пересічні)

315

множини. Ця властивість наближає подібні НМ до умов

реального життя.

Розглянута НМ має кілька "вузьких місць". По-перше, у

процесі навчання може виникнути ситуація, коли великі

позитивні або негативні значення вагових коефіцієнтів

змістять робочу точку на сигмоїдах багатьох нейронів в

область насичення. Малі величини похідної від логістичної

функції приведуть у відповідність

із (12.19) і (12.20) до

припинення навчання, що паралізує НМ. По-друге,

застосування методу градієнтного спуску не гарантує, що буде

знайдено глобальний, а не локальний мінімум цільової

функції. Ця проблема зв'язана ще з однію, як-от - із вибором

величини швидкості навчання. Доказ збіжності навчання в

процесі зворотного поширення засновано на похідних,

тобто

зміна вагових коефіцієнтів і, отже, швидкість навчання

повинні бути досить малими, однак у цьому випадку навчання

буде відбуватися неприйнятно повільно. З іншого боку,

занадто великі корекції вагових коефіцієнтів можуть привести

до нестійкості процесу навчання. Тому

звичайно

вибирається менше 1, але не дуже маленьке, наприклад, 0.1, і

воно може поступово зменшуватися в процесі навчання. Крім

того, для виключення випадкових влучень у локальні

мінімуми іноді, після того як значення вагових коефіцієнтів

застабілізуються,

короткочасно сильно збільшують, щоб

почати градієнтний спуск із нової точки. Якщо повторення цієї

процедури кілька разів приведе алгоритм у той самий стан

НМ, можна більш-менш упевнено сказати, що знайдений

глобальний максимум, а не якийсь іншій.

Серед різних конфігурацій штучних нейронних мереж

зустрічаються такі, при класифікації яких за принципом

навчання,

строго кажучи, не підходять ні навчання з учителем

, ні навчання без учителя . У таких мережах вагові коефіцієнти

синапсів розраховуються перед початком функціонування

мережі на основі попередньої інформації, і все навчання

мережі зводиться саме до цього розрахунку. З одного боку,

пред'явлення апріорної інформації можна розцінювати, як

316

допомогу вчителя, але з іншого боку - мережа фактично

просто запам'ятовує зразки до того, як на її вхід надходять

реальні дані, і не може змінювати своє поведінку, тому

говорити про ланку зворотного зв'язку не доводиться. Серед

мереж із подібною логікою роботи найбільше відомі мережа

Хопфілда і мережа Хемінга, що звичайно

використовуються

для організації асоціативної пам'яті. Далі мова йтиме саме про

них.

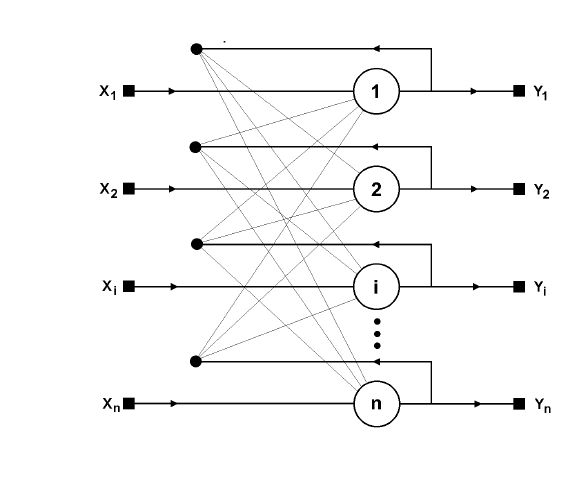
Структурна схема мережі Хопфілда наведена на

рис.12.6. Вона складається з одного шару нейронів, число яких

є одночасно числом входів і виходів мережі. Кожний нейрон

зв'язаний синапсами з всіма іншими нейронами, а також має

один вхідний синапс, через

який здійснюється введення

сигналу. Вихідні сигнали, як звичайно, утворяться на аксонах.

зворотний зв’язок

вхід

вихід

Рис.12.6. Структурна схема мережі Хопфілда

Задача, розв'язувана даною мережею формулюється в

такий спосіб. Відомий деякий набір двійкових сигналів

317

(зображень, звукових оцифровок, інших даних, що описують

деякі об'єкти або характеристики процесів), що вважаються

зразковими. Мережа повинна вміти з довільного неідеального

сигналу, поданого на її вхід, виділити ("згадати" по частковій

інформації) відповідний зразок (якщо такий є) або "дати

висновок" про те, що вхідні дані не відповідають жодному зі

зразків.

У загальному випадку, будь-який сигнал може бути

описаний вектором

{

}

Xxi n

==−:...01, - число нейронів

у мережі і розмірність вхідних і вихідних векторів. Кожний

елемент

дорівнює або +1, або -1. Позначимо вектор, що

описує

-й зразок, через

, а його компоненти, відповідно,

, - число зразків. Коли мережа розпізнає

(або "згадає") якийсь зразок на основі пред'явлених їй даних, її

виходи будуть містити саме його, тобто

xk m

,...= 0 m

, де

вектор вихідних значень мережі:

{

}

Yyi n

==−:...01. У

противному випадку, вихідний вектор не збіжиться з жодний

зразковим.

Якщо, наприклад, сигнали являють собою деякі

зображення, то, відобразивши у графічному вигляді дані з

виходу мережі, можна буде побачити картинку, яка цілком

співпадає з однією зі зразкових (у випадку успіху) або ж

"вільну імпровізацію" мережі (у випадку невдачі).

На стадії

ініціалізації мережі вагові коефіцієнти синапсів

встановлюються в такий спосіб :

xx i j

≠

⎧

⎨

⎪

⎩

⎪

−

∑

(12.29)

Тут

і i

- індекси, відповідно, предсинаптичного і

постсинаптичного нейронів;

-i -й і xx

-й елементи

вектора

-го зразка.

318

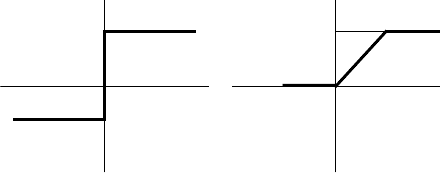
Алгоритм функціонування мережі наступний (

- номер

ітерації):

1. На входи мережі подається невідомий сигнал. Фактично

його введення здійснюється безпосередньою установкою

значень аксонів:

yxi n

−

,...01,

тому позначення на схемі мережі вхідних синапсів у

явному вигляді носить чисто умовний характер. Нуль у

дужках справа від

означає нульову ітерацію в циклі

роботи мережі.

2. Розраховується новий стан нейронів

sp wyp

jiji

)

() (+=

−

∑

−

01..., (12.30)

і нові значення аксонів

[

]

yp fsp

() ()+= +11

(12.31)

де f - активаційна функція у вигляді стрибка, наведена на

рис12.7.а).

а)

-1

б)

Рис.12.7. Активаційні функції

3. Здійснюється перевірка, чи змінилися вихідні значення

аксонів за останню ітерацію. Якщо так - перехід до пункту

2, інакше (якщо виходи застабілізувались) - кінець. При

цьому вихідний вектор являє собою зразок, який

щонайкраще сполучиться з вхідними даними.

Як говорилося вище, іноді мережа не може провести

розпізнавання. Це зв'язано з

проблемою обмеженості

можливостей мережі. Для мережі Хопфілда число зразків m

що запам'ятовуються не повинно перевищувати величини

319

015.n. Крім того, якщо два зразки А та Б сильно схожі, вони,

можливо, будуть викликати в мережі перехресні асоціації,

тобто пред'явлення на входи мережі вектора А приведе до

появи на її виходах вектори Б та навпаки.

Коли непотрібно, щоб мережа в явному вигляді видавала

зразок, а достатньо одержувати його номер, асоціативну

пам'ять успішно реалізує мережа Хемінга. Дана мережа

характеризується, у порівнянні з мережею Хопфілда, меншими

витратами на пам'ять і обсягом обчислень, що стає очевидним

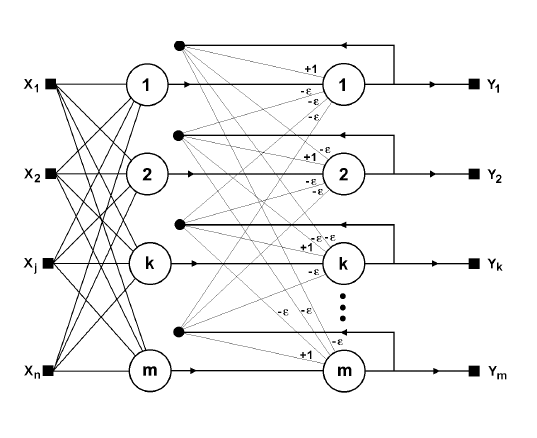
із її структури (рис.12.8).

зворотний зв’язок

вхід

вихід

1 шар 1 шар

Рис.12.8. Структурна схема мережі Хемінга.

Мережа складається з двох шарів. Перший і другий шари

мають по

нейрони, де - число зразків. Нейрони першого

шару мають по n синапсів, з'єднаних із входами мережі

(утворюючи фіктивний нульовий шар). Нейрони другого шару

зв'язані між собою інгібіторними (негативними зворотними)

синаптичними зв'язками. Єдиний синапс із позитивним

зворотним зв'язком для кожного нейрона з'єднаний із його ж

аксоном.

m m

320

Ідея роботи мережі полягає в мінімізації відстані Хемінга

від тестованого зразка до всіх зразків. Відстанню Хемінга

називається число бітів, що відрізняються, у двох бінарних

векторах. Мережа повинна вибрати зразок із мінімальною

відстанню Хемінга до невідомого зразка, у результаті чого

буде активізований тільки один вихід мережі, що відповідає

цьому зразку.

На стадії

ініціалізації ваговим коефіцієнтам першого шару

і порогові активаційної функції привласнюються наступні

значення:

, in

−

01... ,

−

0... 1 (12.32)

−

01...

Тут

- -й елемент x

- го зразка.

Вагові коефіцієнти гальмуючих синапсів у другому шарі

беруть рівними деякій величині

/m. Синапс

нейрона, зв'язаний із його ж аксоном має вагу +1.

Алгоритм функціонування мережі Хемінга наступний:

1. На входи мережі подається невідомий вектор

, виходячи з якого розраховуються

стани нейронів першого шару (верхній індекс у дужках

указує номер шару):

{

Xxi n

==−:...01

}

jj iji

() ()11

== +

ys wxT

−

∑

−

01..., (12.33)

Після цього отриманими значеннями ініціалізуються значення

аксонів другого шару:

= ,

−

01...

2. Обчислюються нові стани нейронів другого шару:

sp yp ypkjj m

jjk

()

()() (),,...

10+= − ≠ = −

−

∑

ε (12.34)

і значення їхніх аксонів:

321