Черняховская Л.Б., Шабанов Л.А.Справочник по статике
Подождите немного. Документ загружается.

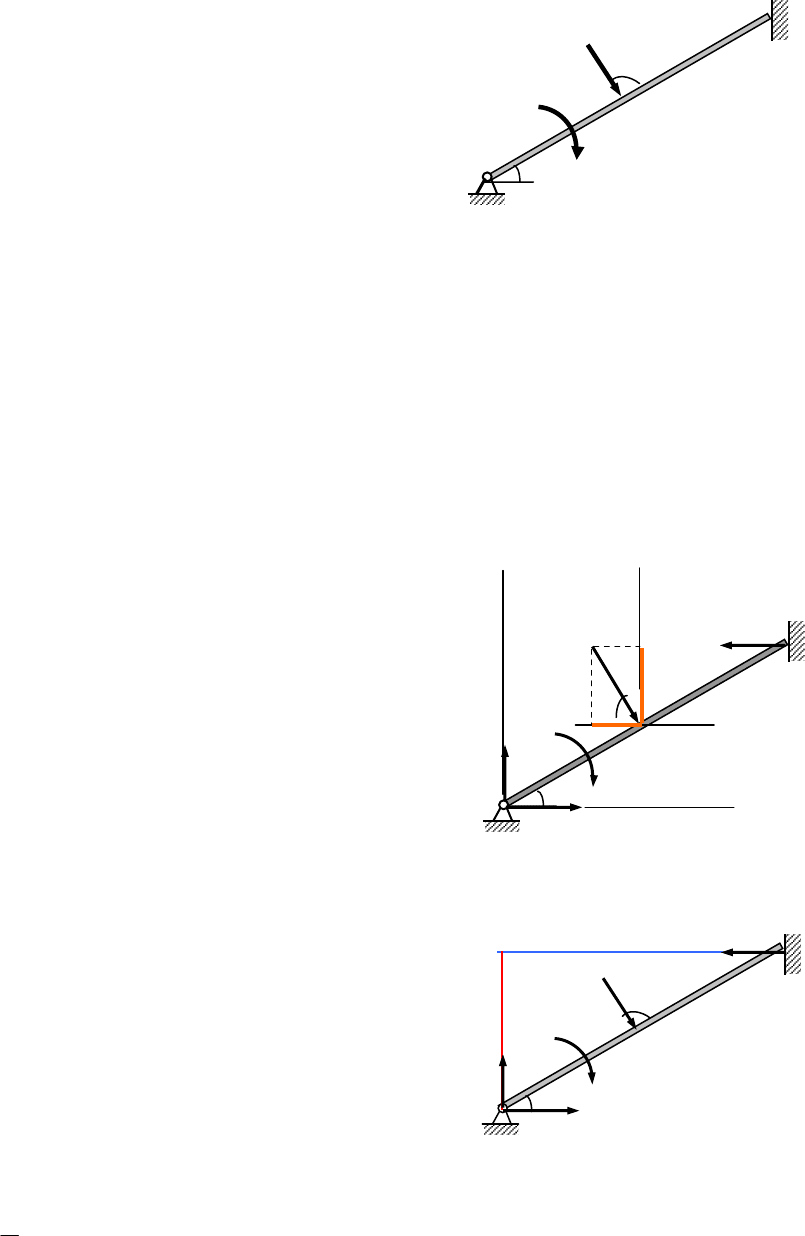
3.5. Пример решения задачи на равновесие плоской системы сил.
Стержень АВ, одним концом закреп-
лен шарнирно, другим опирается на глад-
кую вертикальную стену. На стержень
действует сила Р = 6 кН и пара сил с мо-
ментом М = 20 кНм, АС = СВ =2 м.
(рис.21).
Определить реакции опор.
Решение.
Выбираем
оси координат: направляем
ось
х горизонтально вправо, ось у – верти-
кально вверх.
Кроме активных сил, на стержень действуют: реакция подшипника,
которую раскладываем на две составляющие: Х
А
, У
А
, и реакция R
B
, на-
правленная перпендикулярно опорной плоскости (рис. 21 а).
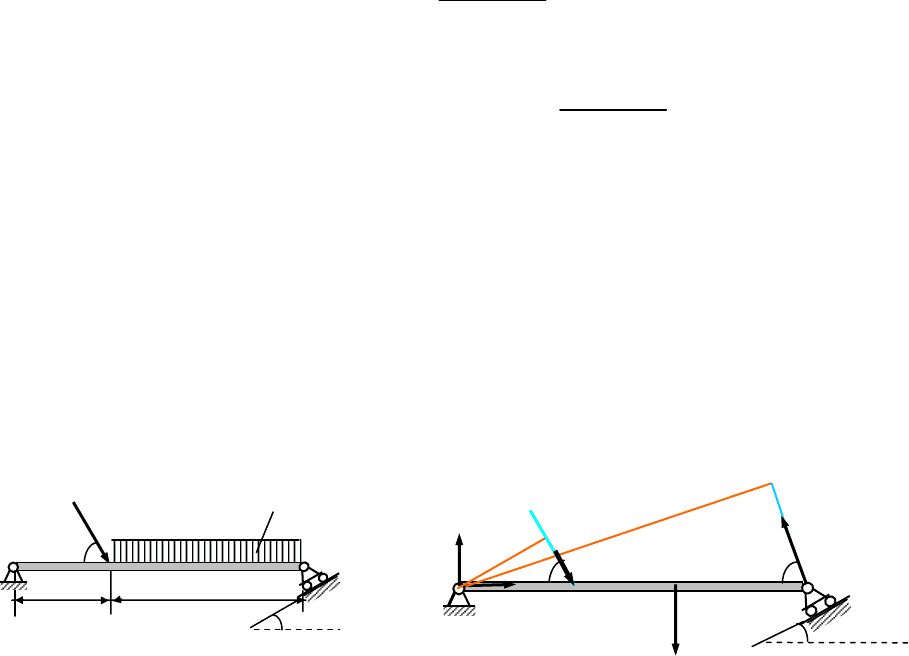
Составим уравнения равновесия. Проведем в точке С, где приложена
сила Р, прямые, параллельные осям х и у.
Проекции силы Р на эти прямые равны
соответственно ее проекциям на оси х и
у:
.60sin,60cos
oo
PPPP
yx
−==
Сумма проекций сил, составляющих
пару, на любую ось, равна нулю.
За центр моментов выбираем точку
А, моменты сил Х
А
, У
А
относительно
этой точки равны нулю, сумма моментов
сил пары относительно любой точки рав-
на моменту пары. Плечом силы Р явля-
ется расстояние АС (рис.21 б), плечом
силы R
B
- перпендикуляр Аа, опущен-
ный из точки А на линию действия этой
силы.
o
АВАа 30sin=
.
Получаем уравнения равновесия:
∑
=−+= 060cos
B
o
AKX
RPXF
∑
=−= 060sin
o
AKY
PYF
∑
=+−−= 030sin)(
o
BKA
ABRACPMFm
.
30
0
90
0
С
Р
А
В
М
Рис.21
Y
A
X
A
60
0
R
B
y
30
0
С
Р
А
В
М
x
Рис.21а
x
1
y
1
a
30
0
90
о
С
Р
А
В
М
R
B
X
A
Y
A
Рис.21б
Из последнего уравнения:
.
30sin
0
AB
ACPM
R
B
+
=
Из второго уравнения:
.60sin
0
PY
A
=
Из первого уравнения:
.
30sin
60cos
0
0
AB
ACPM
PX
A
+
+−=
Численные значения реакций находим после подстановки в полученные
выражения исходных данных.
3.6. Задачи для самостоятельного решения
В следующих задачах (рис. 22 - 27) определить реакции опор в точках А и В.
Задача 1
(рис. 22)
Методические рекомендации
.
Замените (рис. 22а) равномерно распределенную нагрузку ее равнодей-
ствующей Q =q CB, приложите Q в середине отрезка СВ в точке D. Изобрази-
те в виде векторов реакции связей. Реакция в точке В направлена перпендику-
лярно опорной плоскости и составляет угол 70
0
с балкой АВ. Реакция шарнира
А имеет две составляющие: Х
А
и У
А
. Уравнения моментов составьте относи-
тельно точки А, приняв во внимание, что плечом для силы Р является опущен-
ный
на ее линию действия перпендикуляр Аа, плечом силы Q – опущенный на
ее линию действия перпендикуляр Ав.
А
Р = 6 кН, q = 2 кH/м
Р
q
В
С
0,8
1,6
20
0
60
0
Рис.22
b
a
P
60
0
20
0
А
В
D
Y
A
X
A
70
0
N
B
Q
Рис. 22а
С
A
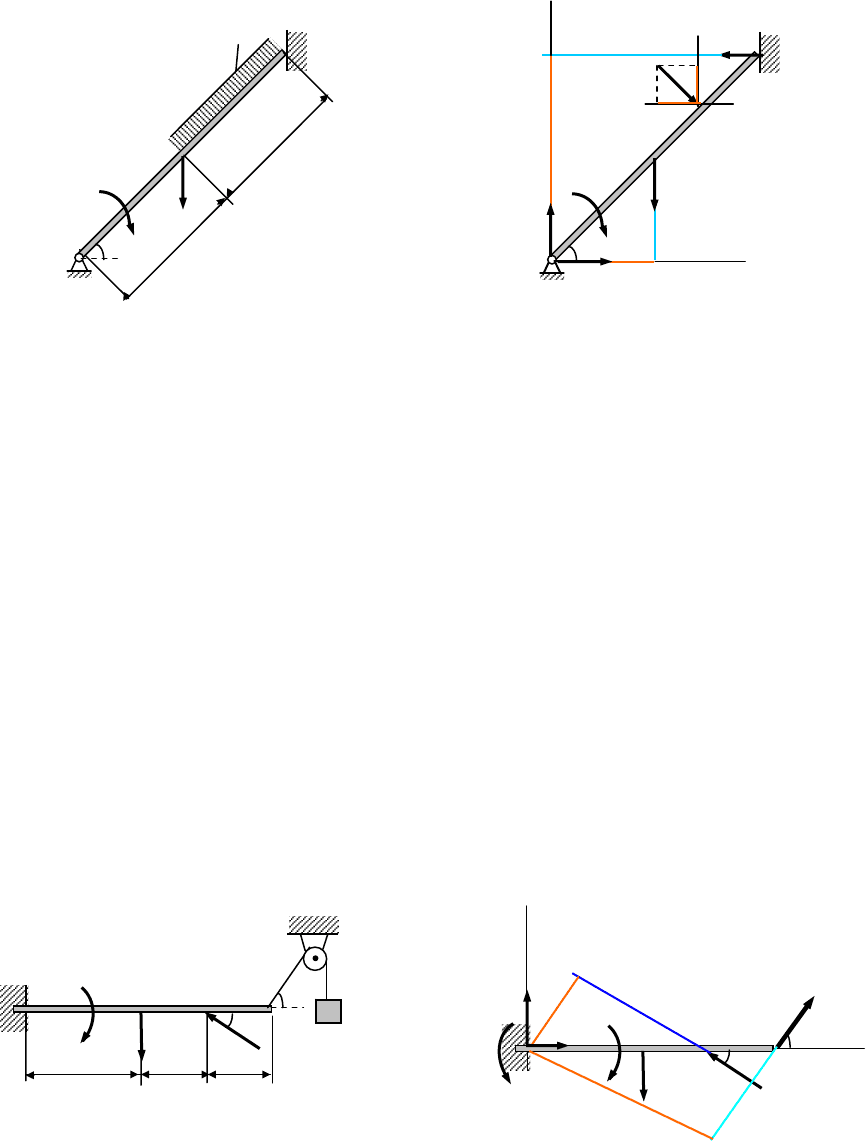
Задача 2 (рис. 23)
Методические рекомендации
Замените равномерно распределенную нагрузку на участке СВ равнодей-
ствующей силой Q = q CB (рис. 23а), приложенной в середине этого участка.
Покажите реакции в точках А и В. Проведите в точке D, где приложена сила
Q, прямые, параллельные осям х и у. С помощью этих прямых найдите проек-
ции силы Q на оси
координат. Составьте уравнения равновесия. Учтите, что
при составлении уравнения моментов относительно точки А плечом силы Р
является отрезок Аа, плечом силы Q – отрезок Ав, плечом силы Q отрезок АD.
Учтите, что сумма проекций сил пары на любую ось равна нулю.
Задача 3 (рис. 24)
Р =10 кН, М = 6 кНм, q =2 кН/м
45
0
А
М
Р
В
С
2
2
q
Рис. 23
Y
A
В
А
М
Р
N
B
Q
b
a
D
X
A
х
у
Рис. 23а
С
45
0
50
0
х
а
у
30
0
A
В
D
P
F
M
У
А
Т
С
в
Х
А
M
А
Рис.24а
С
2
30
0
A
В
D
P
F
M
1
1
Q
50
0
Рис.24
М=12кHм, P=8кНм, Q=10кН, F=6кН.
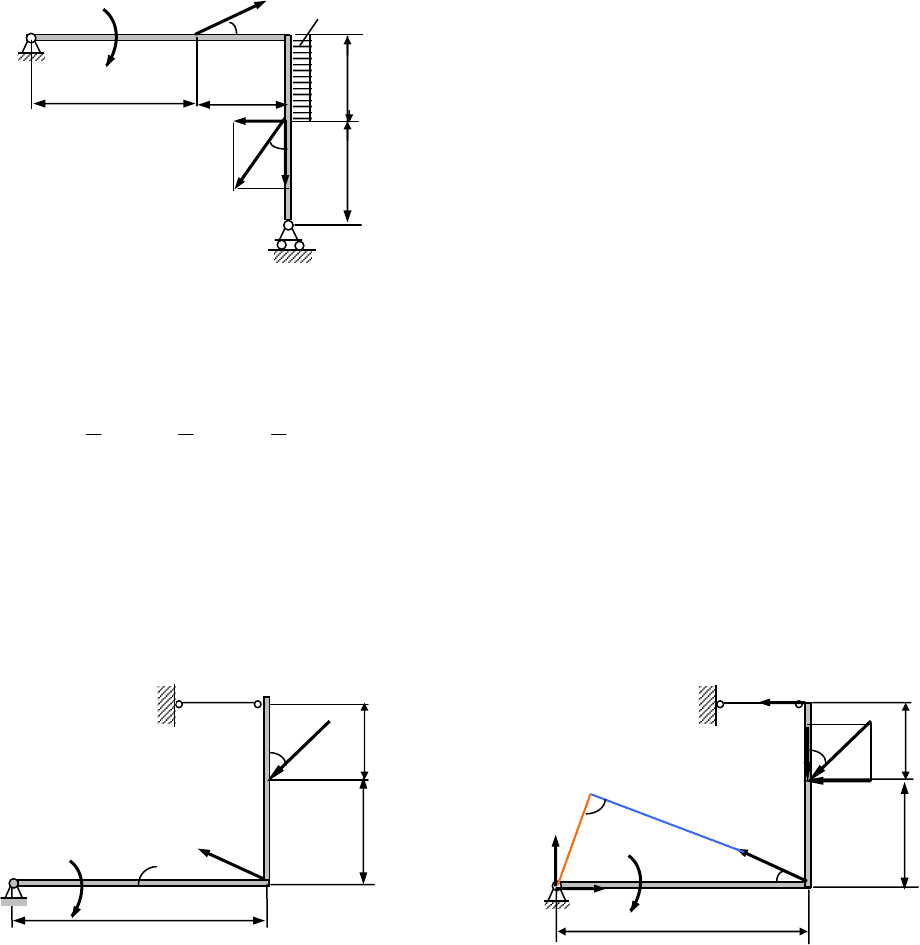
Методические рекомендации.
Покажите реакции связей (рис. 24а). В точке А – жесткая заделка, ее ре-
акцию составляют силы
Х
А
, У
А
и пара сил с моментом М
А
. Реакция нити в
точке В равна силе тяжести груза, подвешенного на этой нити: T =Q. Со-
ставьте уравнения равновесия и определите составляющие реакции жесткой
заделки в точке А: Х
А
, У
А
и М
А
.
Задача 4 (рис. 25)
Методические рекомендации
Покажите на схеме все дейст-
вующие на тело активные силы и ре-
акции связей (рис. 25). Реакцию шар-
нира в точке А разложите на две со-
ставляющие Х
А
и У
А
, реакцию в точке
В направьте перпендикулярно опорной
плоскости. Замените равномерно рас-
пределенную нагрузку на участке СК
ее равнодействующей.
Учтите, что сумма проекций сил,
составляющих пару, на любую ось
равна нулю. При составлении уравне-
ния моментов относительно точки А следует силу F разложить на горизон-
тальную и вертикальную составляющие F
1
и F
2
и применить теорему Ва-
риньона
:
ACFCKFACFCKFFmFmFm
AAA
00
2121
50sin50cos)()()( −−=−⋅−=+= .
Задача 5
(рис. 26).
М
=
34 кНм, Р
=
12 кН,
F
=
20 кH
Рис. 26
4
а
D
С
B
50
0
30
o
F
P
M
4
1,2
1
8
P
1
P
2
А
S
Х
А
У
А
Рис.26а
30
0
F
M
1
,
8
B
50
0
P
1,2
А
М
=
34 кНм, Р
=
12 кН,
F
=
20 кH
P
А
D
С
B
K
40
o
30
o
F
1
M
3
1
1,5
1,8
q
Рис.25
F
2
F
Методические рекомендации.
На схеме (рис.26а) показаны все приложенные к телу силы: заданные
силы Р, F и пара сил с моментом М и реакции связей X
А
, У
А
в точке А и
усилие S в точке В. Составьте уравнения равновесия. Проекции сил пары на
оси координат равны нулю. Плечо силы F относительно точки А равно от-
резку Аа. Для определения момента силы Р относительно точки А следует
разложить ее на две составляющие Р
1
и Р
2
и применить теорему Вариньона.
Р
1
=Рсоs50
0
, P
2
=Psin50
0
.
.50sin50cos)()()(
00
2121
CDPACPCDPACPPmPmPm
AAA
+−=+−=+=
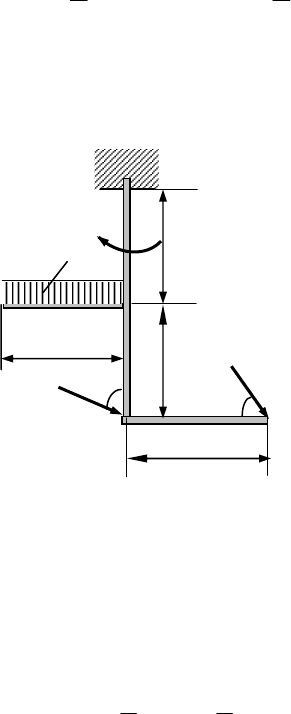
Задача 6 (рис. 27)
M = 34 кНм, Р = 18 кН, F = 10 кН, q = 2 кН/м.
Методические рекомендации
Проверьте (рис. 27), является ли задача стати-
чески определенной. Выберите оси координат:
ось х горизонтально, ось у вертикально.
Покажите реакции в жесткой заделке в точке
А : силы Х
А
, У
А
и пару сил с моментом М
А
. Заме-
ните равномерно распределенную нагрузку на
участке ED ее равнодействующей Q =q ED, при-
ложенной в середине этого участка. Разложите
силу Р на две составляющие Р
1
и Р
2
. Р
1
направьте
горизонтально, Р
2
– вертикально.
Тогда Р
1
=Р соs 60
0
, P
2
=Psin 60
0
.
Составьте уравнения равновесия. Уравнение
моментов составьте относительно точки А. Момент силы Р определите с
помощью теоремы Вариньона:
CBPACPCBPACPPmPmPm
AAA
00
2121
60sin60cos)()()( −=−=+=
B
1,5
Рис. 27
60
0
P
M
2
А
D
С
70
0
F
E
q
2
2
4. Трение.
4.1. Силой трения называется сила, возникающая при стремлении
сдвинуть одно тело по поверхности другого в плоскости соприкосновения
тел
. Возникновение силы трения обусловлено шероховатостью трущихся по-
верхностей.
Трение, возникающее при стремлении сдвинуть тело, находящееся в
равновесии, по шероховатой поверхности, называется статическим. Сила
статического трения может принимать любые значения от нуля до не-
которого максимального значения. Максимальная величина статического
трения соответствует моменту начала скольжения трущихся тел и
равна произведению коэффициента статического трения на нормальную
реакцию:
NfF
o
=
max
.
Статический коэффициент трения f
o
определяется опытным путем и зави-
сит от материала соприкасающихся тел шероховатости их поверхностей.
Благодаря наличию силы трения между данным телом и
опорной поверхностью полная реакция
R
этой поверхности
является равнодействующей двух сил: нормальной реакции
N
и силы трения F (рис.28).
Угол ϕ между направлениями нормальной реакции
N
и
полной реакции
R
, соответствующий максимальному значе-
нию силы трения, называется углом трения.
o
o
f
N
Nf
N
F
tq ===
max
ϕ
.
Метод решения задач статики при наличии трения сводится к со-
ставлению уравнений равновесия, но только в эти уравнения, кроме задан-
ных сил, приложенных к данному телу, и реакций связей, войдут еще и
силы трения. К уравнениям равновесия добавляется формула, определяю-
щая максимальную величину силы трения, которая определятся по фор-
муле
NfF
o
=
max
.
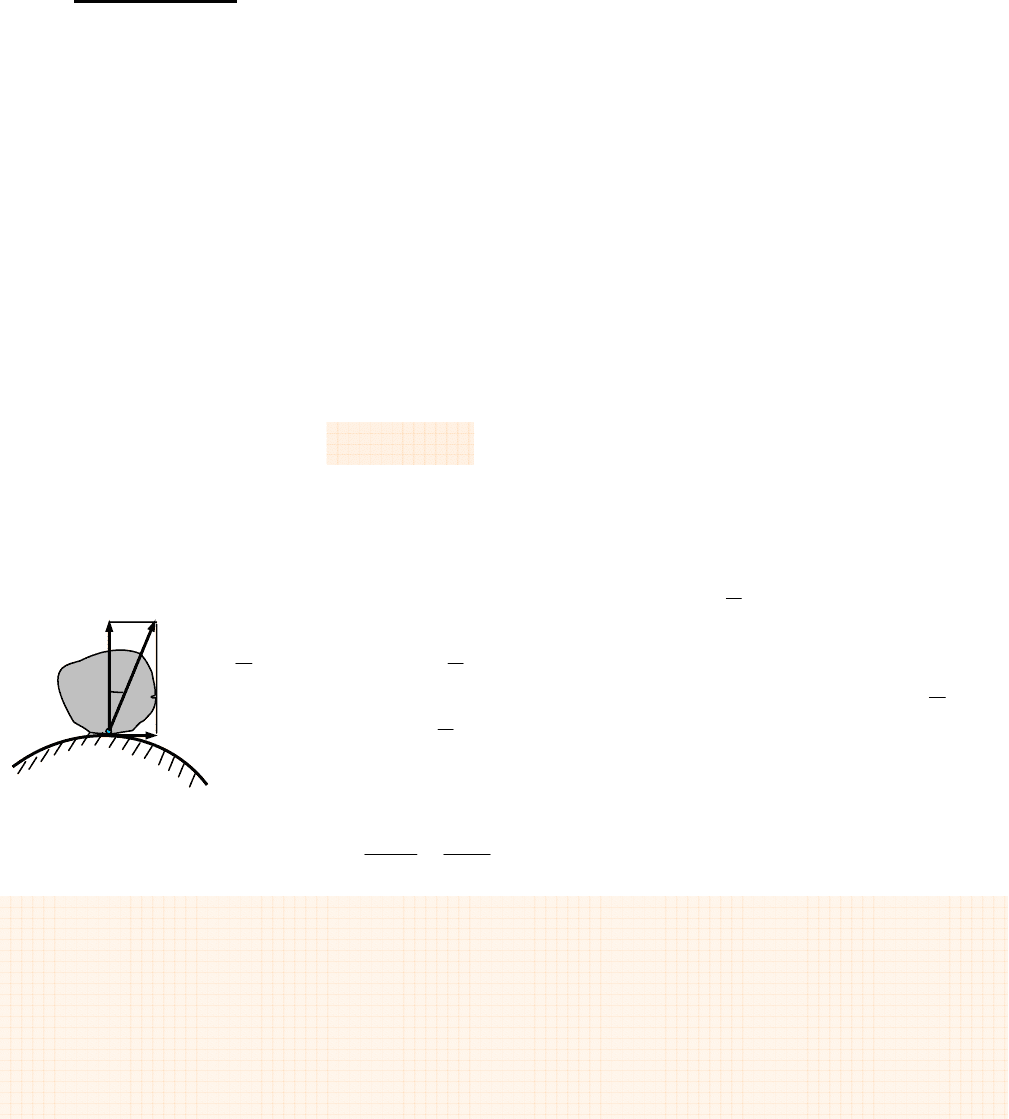
4.2. Примеры решения задач с учетом сил трения
Пример 1
. Груз массой m лежит на горизонтальной плоскости. Опреде-
лить, какую силу P, направленную под углом α к этой плоскости, необходимо
приложить к телу, чтобы сдвинуть его с места, если коэффициент трения груза
о плоскость равен f (рис. 29).
ϕ
F
N R
Рис. 28
Решение.
Рассмотрим предельное положение равно-
весия груза. На груз действуют сила тяжести m
q,
нормальная реакция N, сила трения F и сила Р.
Составляем уравнения равновесия груза.
,0cos =−=
∑
FPF
kx
α
∑
=−+= .0sin mqNPF
ky
α
Находим нормальную реакцию N из по-
следнего уравнения:
α
sinPmqN −
=
. Мак-
симальная сила трения
)sin(
α
PmqffNF
−
=
=
. Подставим это значение в
первое уравнение и определим предельное значение силы Р, при котором груз
остается в равновесии.
αα
sincos f
fmq
P
пр
+
=
.
Движение груза начнется при значениях
пр
PP ≥
.
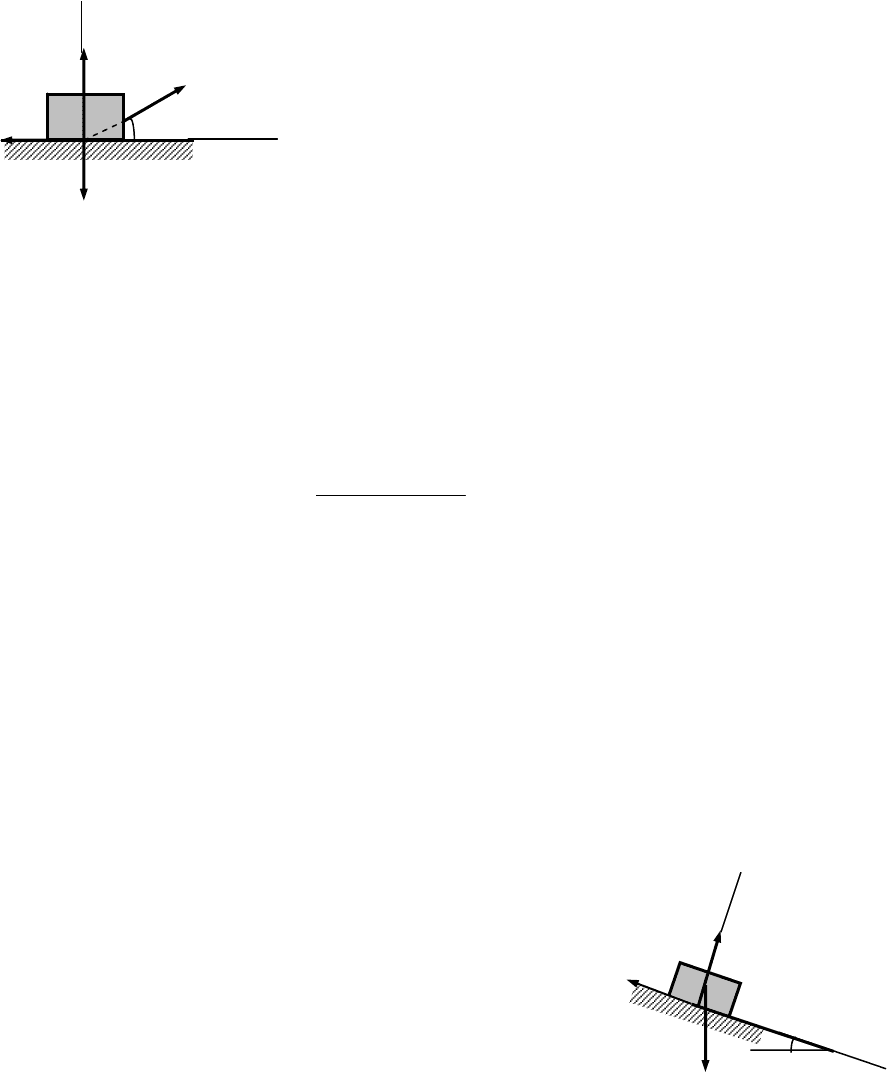
Пример 2. Определить, при каких значениях угла наклона α груз, находя-
щийся на наклонной плоскости, остается в равновесии, если его коэффициент
трения равен f (рис.30).
Решение.
Рассмотрим предельное положение равновесия груза на наклонной плоско-
сти. На груз действуют сила тяжести m
q, нормальная реакция N и сила трения
F. Уравнения равновесия:
0sin =−=
∑
FmqF
kx
α
,
∑
=−= 0cos
α
mqNF
ky
.
Из первого уравнения получаем
α
sinmqF
=
.
(1)
Из второго уравнения определяем нормальную
реакцию:
α
cosmqN =
.
Максимальное значение силы трения
α
cosmqffNF
=
=
. (2)
Приравниваем (1) и (2):
α
sinmq
α
cosmqf
=
и получаем
ftq
=
α
.
Следовательно, равновесие груза возможно при углах наклона α, удовле-
творяющих неравенству
:
ftq
≤
α
.
N
F
P
mq
α
х
у
Рис.29
N
F
m
q
х
у
Рис. 30
α
4.3. Задача для самостоятельного решения
Лестница опирается на гладкую стену и негладкий горизонтальный пол.
Коэффициент трения равен f (рис. 31). Под каким углом α к полу нужно по-
ставить лестницу, чтобы человек мог подняться по ней доверху. Вес лестницы
– Р, вес человека – р.
Методические рекомендации
Убедитесь, что задача статически определенная.
Выберете оси координат: ось х – горизонтально, ось у – вертикально. По-
кажите на схеме все силы, приложенные к лестнице. Силу тяжести человека
приложите в точке А, силу тяжести лестницы – в середине лестницы в точке
С. Реакция N
A
в точке А направлена перпендикулярно опорной стене. Реакция
в точке В состоит из нормальной составляющей N
B
и силы трения F. Макси-
мальная сила трения, при котором сохраняется равновесие, равна F=f N
В
.
Составьте уравнения равновесия для сил приложенных к лестнице. Урав-
нение моментов можно составить как относительно точки А, так и относи-
тельно точки В.

5. Равновесие системы твердых тел.
5.1. Метод расчленения.
В случае равновесия системы твердых тел, соединенных между собой,
действующие на систему силы разделяются на внешние и внутренние.
Внешними называются силы, с которыми тела, не входящие в систему,
действуют на тела системы
.
Внутренними называются силы взаимодействия между телами систе-
мы
.
Внутренние силы попарно равны по модулю и противоположны по на-
правлению, поэтому алгебраическая сумма моментов внутренних сил относи-
тельно любой точки равна нулю, а также равна нулю сумма их проекций на
любую координатную ось.
Уравнения равновесия, составленные для системы тел, не содержат внут-
ренних сил, и из них можно найти
только внешние реакции, если их число не
более трех.
Если же число внешних сил более трех, то для их определения, а
также для нахождения внутренних сил следует применить метод рас-
членения, т.е. рассмотреть равновесие каждого тела в отдельности,
учитывая все силы, приложенные к этому телу
.
При равновесии системы тел каждое тело, входящее в систему, также
находится в равновесии, следовательно, для системы, состоящей из n тел,
можно составить 3n уравнений равновесия. Кроме того, при необходимости
можно составить еще три уравнения равновесия для всей системы тел, но в эти
уравнения не входят внутренние силы.
Если система
состоит из двух тел, то, применяя метод расчленения, по-
лучим шесть уравнений равновесия, кроме того, для всей системы можно со-
ставить еще три уравнения.
5.2. Рекомендации для решения задач на равновесие системы
соединенных тел.
1.Изобразить на чертеже систему тел, находящуюся в равновесии, а
затем каждое тело в отдельности.
2. Показать в виде векторов внешние и внутренние силы, в число ко-
торых входят все активные силы и силы реакции.
3. Сопоставить число неизвестных сил и число независимых уравнений
равновесия для выяснения, является ли задача статически определенной.
4. Рассмотреть равновесие каждого тела в отдельности и составить
соответствующие уравнения равновесия.
5.Составить, если это необходимо, уравнения равновесия для всей сис-
темы тел.
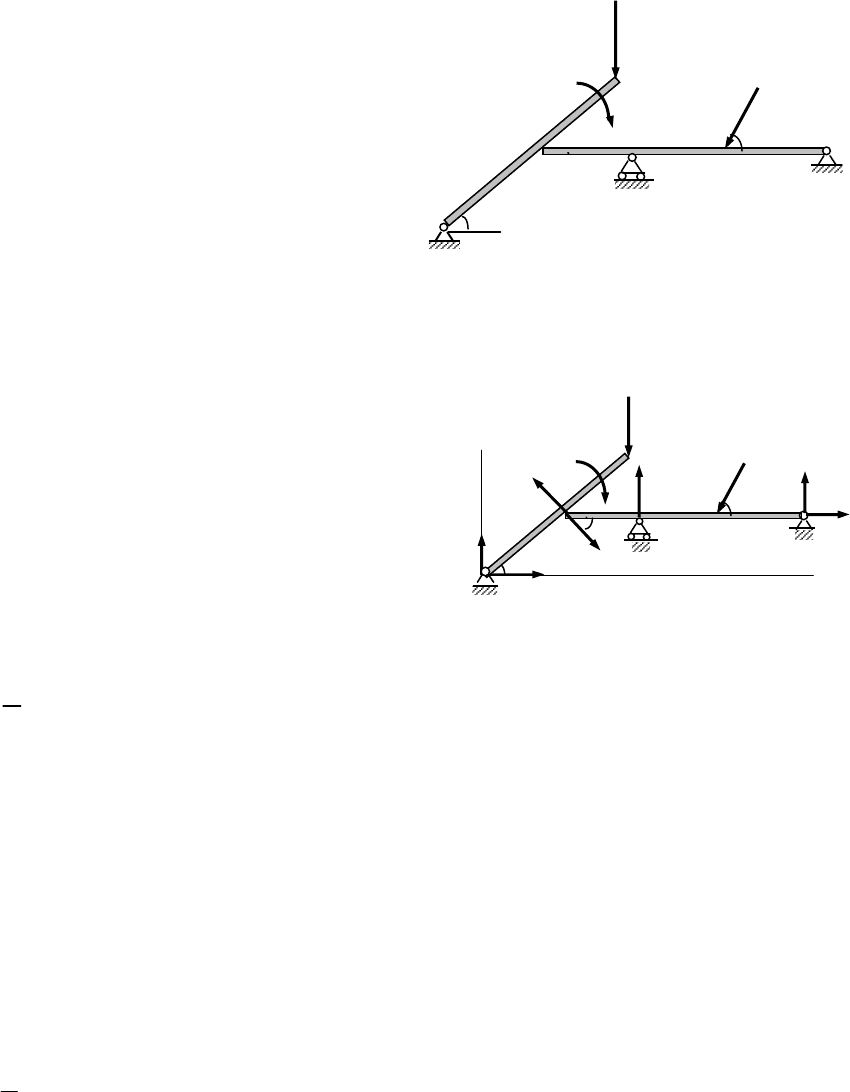
Пример.
Стержень АВ в точке С опирается на стержень СD (рис. 32).
Определить реакции в точках А, С,
Е и D, если Р = 200 Н, F = 400 H,АС
=СВ =в =3 м, СЕ = ЕК = КD = a = 2
м, М=300 Нм.
Решение.
На составную конструкцию дейст-
вуют активные силы Р и Q, пара сил
с моментом М, а также подлежащие
определению шесть реакций Х
А
, У
А
,
Х
D
, Y
D
, N
E
, и N
C
., при этом N
C
= -
N
C1
.
Покажем на чертеже направления
всех реакций как внешних, так и внут-
ренних, и составим уравнения равнове-
сия для всей конструкции (рис. 32а).
∑
=−+= ,060cos
o
DA
FXXF
kx
∑
=−−++= 060sin PFNYYF
o
EDA
ky
.
∑
−++++−= )40cos()40cos(40sin)( CEACNCDACYACXFm
o
E
o
D
o
DA
k
0)40cos(60sin40sin60cos40cos =+−+−− CKACFACFPABM
ooooo
. (1)
В эти три уравнения входят пять неизвестных реакций Х
А
, У
А
, Х
D
, Y
D
, N
E
.
Сделаем чертежи и рассмотрим равновесие каждого тела.
Выбираем оси координат и составляем уравнения равновесия для стержня
АВ (рис.32б).
∑
=−= 050cos
o
CA
NXF
kx
∑
=−+= 050sin PNYF
o
CA
ky
040cos)( =⋅−−⋅=
∑
o
CA
ABPMACNFm
k
(2)
A
D
E
K
F
60
0
C
40
0
P
B
М
Рис. 32
Рис. 32а
A
P
D
E
K
Y
D
F
60
0
N
C1
N
E
50
0
B
C
Y
A
N
C
40
0
X
D
М
у
х
