Ченцов С.В. Автоматизированное проектирование средств и систем управления
Подождите немного. Документ загружается.


ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 7. Алгоритмы и методы анализа статических режимов ССУ в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
111
Для итерационных методов решения систем ЛАУ И >> 1,
K
2
, где
К – среднее арифметическое для числа ненулевых элементов в одной строке
матрицы А. Так, для моделей переключательных электронных схем по ре-
зультатам статистических исследований
8,7
, т. е. одна итерация выполня-
ется быстрее, чем по методу Гаусса. Однако из-за того, что И >> 1 итераци-
онные методы по показателю Тм практически всегда проигрывают прямым
методам.
Решение систем НАУ выполняется итерационными методами, при этом
на требуемое число итераций И в методе Ньютона решающее влияние оказы-
вает выбор начального приближения; в други
х итерационных методах – z
(число обусловленности) матрицы Якоби решаемой системы уравнений.
В методе Ньютона, применяемом в рамках методов установления или про-
должения решения по параметру, обычно И не превышает трех (И
3).
В случаях, если И превышает некоторый порог И
пр
(например, И
пр
= 7), луч-
ше уменьшать значения коэффициентов, управляющих процессом установ-
ления, чем продолжать итерации при И > И
пр
. При решении НАУ величина
растет, так как при ее подсчете должны быть учтены затраты на вычисление
элементов матрицы Якоби.
В методе простых итераций И может достигать неприемлемо больших
значений, поэтому на И вводится ограничение И
гр
= 1,5·104. Из соотношения
И
гр
=
lg5,0 z , при
3
10
получаем, что метод простых итераций можно
использовать только при решении системы НАУ, у которых матрица Якоби
имеет z < 104. Методы Зейделя, Якоби, последовательной верхней релакса-
ции имеют аналогичный характер зависимости И от z, хотя скорость сходи-
мости у них часто оказывается несколько выше, чем в методе простых итера-
ций.
Экономичность метода решения системы АУ о
пределяется затратами
ОЗУ. На хранение матрицы Якоби нужно n
2
ячеек памяти. В задачах анализа
распределенных моделей, в которых n > 10
4
, экономичность становится важ-
ной характеристикой.
Точность решения определяется обусловленностью и значениями по-
грешностей ε
1
и ε
2
, задаваемых пользователем САПР. Задаваемые значения ε
1
и ε
2
могут оказаться недостижимыми или из-за несходимости, или из-за
слишком медленной сходимости вычислительного процесса. Поэтому если
создаваемая САПР ориентирована на решение систем уравнений с широким
диапазоном значений z, то разработчику системы нужно принимать специ-
альные меры по обеспечению точности решения.
Надежность метода определяется не только фактом сходимости к кор-
ню, но и тем, каков
ы затраты времени Тм на получение решения с требуемой
точностью. Ненадежность итерационных методов проявляется либо при не-
удачном выборе начального приближения к точному решению (метод Нью-
тона), либо при плохой обусловленности задачи (метод простых итераций),
либо при повышенных требованиях к точности решения (метод простых ите-
раций), либо при высокой размерности задачи (метод Гаусса при неучете

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 7. Алгоритмы и методы анализа статических режимов ССУ в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
112
разреженности). Поэтому при создании специализированных САПР необхо-
димы предварительный анализ особенностей ММ заданного класса задач
(значений n, z, допустимых погрешностей) и соответствующий выбор кон-
кретного метода. При создании универсальных САПР необходима реализа-
ция средств адаптации метода решения к конкретным условиям. Такая адап-
тация чаще всего применяется в рамках методов установления или продол-
жения решения по параметру.
Таки
м образом, алгоритмы и методы анализа статических режимов СУ
в современных САПР есть прежде всего алгоритмы и методы решений ли-
нейных и нелинейных алгебраических уравнений математической модели СУ
для разных уровней описания систем. При этом применение традиционных
частотных методов анализа устойчивости и качества трансформируется в об-
работку результ
атов численного решения систем ЛАУ. Например, в широко
применяемом формате Spice проектировщику для получения наглядных ха-
рактеристик системы ЛАХ и ФЧХ достаточно ввести эквивалентную схему
замещения устройства или СУ, выполнить анализ частотных характеристик
(расчет системы ЛАУ ММ устройства или СУ) и вывести графические ре-
зультаты моделирования с использованием правил языка проектирования.
Л
Л
е
е
к
к
ц
ц
и
и
я
я
8
8
.
.
А
А
л
л
г
г
о
о
р
р
и
и
т
т
м
м
ы
ы
и
и
м
м
е
е
т
т
о
о
д
д
ы
ы
а
а
н
н
а
а
л
л
и
и
з
з
а
а
С
С
С
С
У
У
в
в
о
о
в
в
р
р
е
е
м
м
е
е
н
н
н
н
о
о
й
й
о
о
б
б
л
л
а
а
с
с
т
т
и
и
в
в
и
и
н
н
т
т
е
е
г
г
р
р
и
и
р
р
о
о
в
в
а
а
н
н
н
н
ы
ы
х
х
С
С
А
А
П
П
Р
Р
Методы анализа СУ во временной области. Методы анализа СУ с
«жесткими» системами уравнений. Основные характеристики методов
анализа СУ во временной области. Алгоритмы автоматического выбора ша-
га. Выбор эффективных методов анализа переходных процессов СУ.
М
М
е
е
т
т
о
о
д
д
ы
ы
а
а
н
н
а
а
л
л
и
и
з
з
а
а
С
С
У
У
в
в
о
о
в
в
р
р
е
е
м
м
е
е
н
н
н
н
о
о
й
й
о
о
б
б
л
л
а
а
с
с
т
т
и
и
Анализ временных оценок качества СУ осуществляется численными
методами решения системы уравнений ММ, которая может быть представле-
на: в виде системы дифференциальных уравнений в неявной форме
0,,
tV
dt
dV
F ; в виде системы дифференциальных уравнений в явной фор-
ме
),( tVF
dt
dV
, где V– вектор фазовых переменных размерностью n.
По исходной ММ СУ строится переходный процесс в системе, по кото-
рому и делаются нужные оценки [5
; 6].
Анализ переходных процессов проектируемого объекта сводится к
численному интегрированию системы ОДУ и нахождению V(t) на заданном
интервале времени [0, Т
кон
], при заданных начальных условиях V(0)=V
0
. При

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
113
решении этой задачи на интервале интегрирования выделяется конечное чис-
ло точек t
k
, в которых определяются значения V, к = 1, 2, …, Ш, где Ш – чис-
ло шагов интегрирования [7
].
В каждой точке t
k
система ОДУ представляется в виде системы n ал-
гебраических уравнений с 2n неизвестными. Система уравнений дополняется
уравнениями, задаваемыми выбранным методом численного интегрирования.
Обобщенная формула методов интегрирования используется для реше-
ния систем ОДУ.
),..,
2
,
1
,,..,
1
,(
pk
V
k
V
k
V
pk
V
k
V
k
VG
k
V
,
(8.1)
где G – некоторая функция, определяемая способом построения метода ин-
тегрирования (чаще всего линейная); p – количество предыдущих точек, ис-
пользованных в формуле интегрирования (порядок метода);
– коэффици-
ент.
Если уравнения составляются для текущего к-го момента времени
(
= 0), то метод явный (иначе, экстраполяционный метод, основанный на
формулах интегрирования вперед).
Если уравнения составляются для следующего (к+1)-го момента вре-
мени (
= 1), то метод неявный (интерполяционный, основанный на форму-
лах интегрирования назад).
Различия между ними удобно показать на примере простейших мето-
дов первого порядка – методов Эйлера. Формула явного метода Эйлера пред-
ставляет собой следующую формулу замены производных в точке t
n
:
1
,
n n n
dV / dt | n (V V ) / h
где индекс равен номеру шага интегрирования; h
n
= t
n+1
– t
n
– размер шага
интегрирования (обычно h
n
называют просто шагом интегрирования).
В формуле неявного метода Эйлера использовано дифференцирование назад:
1nn- n
dV / dt | n (V V ) / h ,
где
1nnn-
h t t .
В зависимости от значения р методы интегрирования распадаются на
два класса: 1) одношаговые, если р = 1; 2) многошаговые, если р > 1, причем
р называют порядком многошагового метода (в формуле интегрирования ис-
пользуют результаты предыдущих шагов).
К
К
л
л
а
а
с
с
с
с
и
и
ф
ф
и
и
к
к
а
а
ц
ц
и
и
я
я
о
о
с
с
н
н
о
о
в
в
н
н
ы
ы
х
х
ч
ч
и
и
с
с
л
л
е
е
н
н
н
н
ы
ы
х
х
м
м
е
е
т
т
о
о
д
д
о
о
в
в
р
р
е
е
ш
ш
е
е
н
н
и
и
я
я
с
с
и
и
с
с
т
т
е
е
м
м
О
О
Д
Д
У
У

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
114
1) Явные:
– блочные,
– одношаговые,
• многоэтапные методы Рунге – Кутты,
• одноэтапные:
– метод Эйлера,
– метод разложения в ряд Тейлора,
– многошаговые:
• метод Адамса – Башфорта,
• методы с сериями шагов.
2) Неявные:
– одно- и двушаговые:
• метод Эйлера,
• метод трапеций.
• Рунге – Кутты
– многошаговые:
• ФДН,
• Адамса – Мултона,
– блочные.
В современных САПР для решения си
стем ОДУ применяются наиболее
распространенные методы ФДН (формулы дифференцирования назад),
Адамса и Рунге – Кутты.
Общий вид формул дифференцирования назад:
k
h
p
i
ik
V
i
a
dt
k
dV
0
,
1
kk k-
h t t
– величина k-го шага интегрирования; а
i
– коэффициент (значе-
ние зависит от порядка метода р).
Аппроксимация производных в точке t
k
производится с помощью зна-
чений, относящихся к данному и предыдущему моментам времени. При р = 1
формула метода ФДН совпадает с неявной формулой Эйлера
k
h
k
V
k
V
k
V
)
1
(
.
Часто используют формулу Гира второго порядка, называемую форму-
лой Шихмана при h = const
31
2/.
12
22
VVV Vh
kk k
k
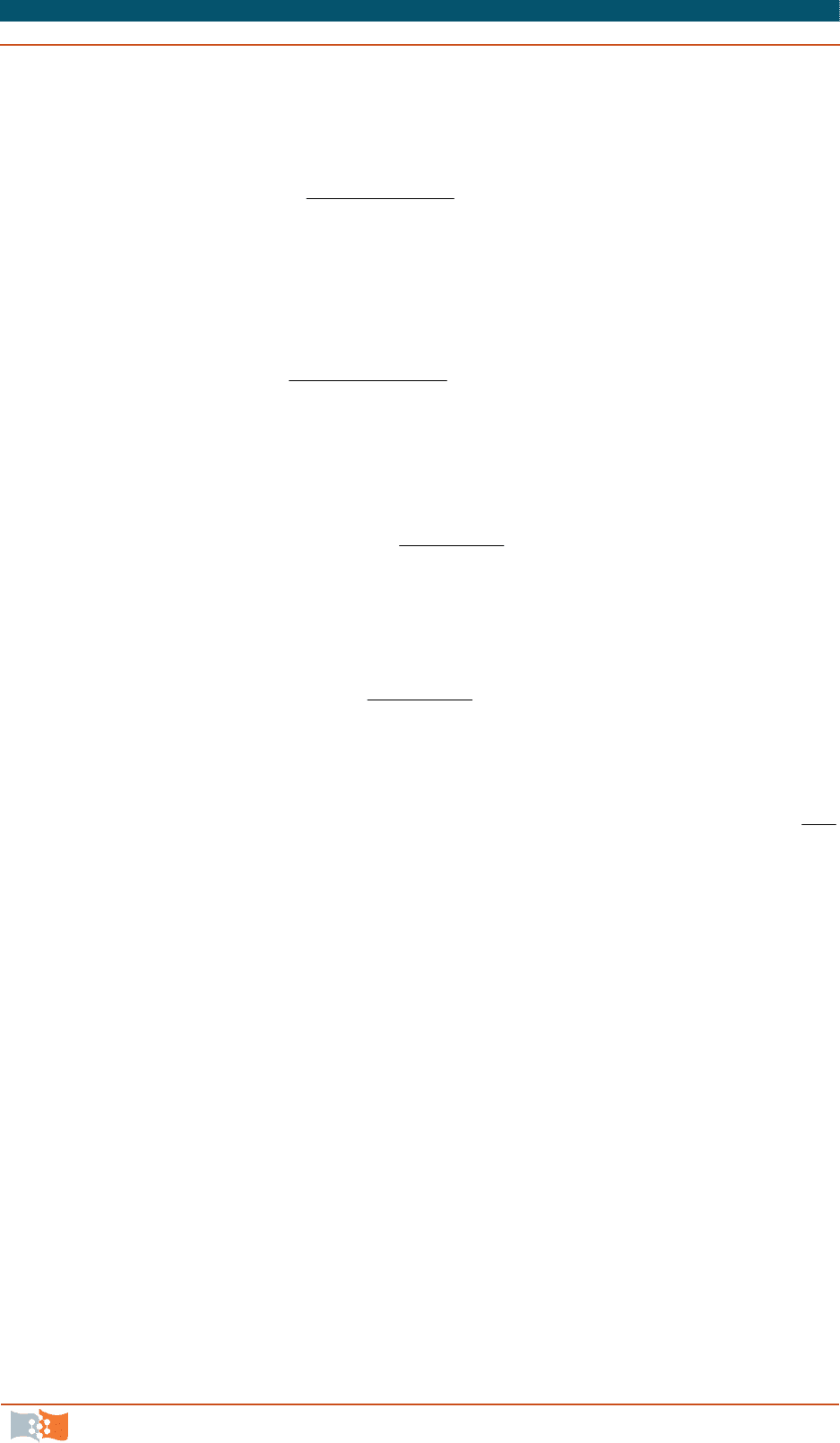
ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
115
Формулы интегрирования при р > 1 в явных методах Адамса имеют
вид
()
11
,
1
2
p
aVV
kk
VaV
iki
k
h
i
k
неявных методах Адамса:
1
()
01
1
p
aVV
kk
VaV
iki
k
h
i
k
,
явная формула Адамса при р = 1 называется явной формулой Эйлера:
k
h
k
V
k
V
k
V
)
1
(
1
,
при р = 2 метод Адамса называют методом трапеций:
1
)
1
(
2
k
V
k
h
k
V
k
V
k
V
.
Методы ФДН являются наиболее распространенными современными
методами интегрирования, основанными на представлении производной
dt
dV
в точке t
k
через значения V
k
и i-ю предысторию, т. е. в точках V
k-1
, V
k-2,
…,V
k-i
.
Их основное преимущество перед другими методами – возможность смены
не только шага интегрирования h, но и порядка метода р, что обеспечивает
высокую точность расчетов характеристик.
Явные методы интегрирования целесообразно использовать при реше-
нии систем ОДУ в форме Коши. Достоинства явных методов: малый объём
вычислений на одном шаге; уменьшение затрат памяти. Явные методы наи-
более лег
ко реализуются, приводят к сравнительно небольшому объему вы-
числений на одном шаге интегрирования. Однако для соблюдения условий
устойчивости приходится уменьшать шаг настолько, что увеличившееся чис-
ло шагов может сделать недопустимо большими общие затраты машинного
времени. Поэтому явные методы, к которым относятся известные методы
Адамса – Башфорта и явные варианты метода Рунге – Кутта, оказываются
малонадежными и в САПР находят ограниченное применение.
Чаще всего используется формула, предложенная Рунге, основанная на вы-
числении приближенного решения y
1
в узле x
0
+ h в виде линейной комбина-
ции с постоянными коэффициентами:

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
116
)(...)()(
221111
hkphkphkpyy
qqqqq
,
(8.2)
),()(
001
yxfhk
,
))(,()(
121002
hkyhxhfhk
,
…………………..
))(...)(,()(
11,1100
hkhkyhxhfhk
qqqqqq
.
Существует семейство формул типа Рунге – Кутта (8.2)
четвертого
порядка точности, для которых q = s = 4. Формула классического метода
Рунге – Кутта
),(
),
2
1
,
2
1
(
),
2
1
,
2
1
(
),,(
),22(
6
1
3004
2003
1002
001
432101
kyhxhfk
kyhxhfk
kyhxhfk
yxhfk
kkkkyy
М
М
е
е
т
т
о
о
д
д
ы
ы
а
а
н
н
а
а
л
л
и
и
з
з
а
а
С
С
У
У
с
с
«
«
ж
ж
е
е
с
с
т
т
к
к
и
и
м
м
и
и
»
»
с
с
и
и
с
с
т
т
е
е
м
м
а
а
м
м
и
и
у
у
р
р
а
а
в
в
н
н
е
е
н
н
и
и
й
й
Особая группа – задачи с «жесткими» системами уравнений (чаще всего
это системы дифференциальных уравнений высокого порядка, описывающие
динамические системы). Для описания процесса нужно использовать функ-
ции двух типов: на малых отрезках – функции с быстро меняющимися пара-
метрами (большие производные) и на остальной части – функции с малыми
производными (медленные движения). Часто в системе ОДУ не у
дается явно
выделить члены с малыми параметрами, однако решение также имеет участ-
ки быстрых и медленных движений.
В частности, система ОДУ будет плохо обусловленной (жесткой), если
выполняется условие
max( )
1,
min( )
i
i
i
i
z
(8.3)
где z – число обусловленности матрицы А. Обычно математическую модель
считают плохо обусловленной (а систему уравнений жесткой), если z > 10
5
.
.

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
117
Метод Гира для жестких систем является многошаговым предсказы-
вающе-исправляющим ФДН методом. При этом формула-предиктор и фор-
мула-корректор имеют один и тот же порядок.
Когда система уравнений является жесткой, интегрирование осуществ-
ляется специальным методом на основе формул дифференцирования назад
(ФДН) вида
k
i
mimim
hbfxax
1
111
.
В методе Гира эти формулы реализованы с помощью вектора Нордсика,
позволяющего использовать эффективный алгоритм автоматического изме-
нения порядка и величины шага. Последние компоненты вектора Нордсика
позволяют получить оценку ошибки. При k = 1 (тогда
1
a
= b = 1) получим не-
явный Эйлера – метод 1-го порядка.
Многошаговые формулы основаны на численном интегрировании, т. е.
интеграл аппроксимируется с помощью какой-либо квадратурной формулы.
Существуют многошаговые методы, воплотившие совсем другую идею –
численного дифференцирования искомой функции. Рассмотрим вывод фор-
мул численного интегрирования для жесткой системы. Метод Гира строится
на основе формул дифференцирования назад
k
i
knknkini
yxfhy
0
0),(
, 1
k
.
(8.4)
Предположим, что начальное приближение для решения уравнения (8.4)
находится по явной формуле вида
1
0
111
),(
k
i
knknkknikn
yxfhyy
.
(8.5)
Обозначим
knm и перепишем формулу (8.5) в следующем виде:
k
i
mmkimikm
yxfhyy
0
111
),(
.
(8.6)
Обозначим
iki
A
,
11
k
B
и заменим m на n. Тогда
k
i
nninin
yxfhByAy
0
111
),( .
Аналогично преобразуем формулу (8.4)
:

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
118
k
i
mmkimikm
yxfhyy
0
),(
.
Обозначим
iki
,
k
b
0
и заменим m на n. Тогда
k
i
nninin
yxfhbyy
0
0
),(
.
Рассмотрим следующий итерационный процесс:
k
i
ninin
fhByAy
0
11
)0(
,
(8.7)
k
i
v
nnini
v
n
yxfhbyy
0
)(
0
)1(
),(
, ,...2,1,0
v .
(8.8)
Из (8.8)
получаем
)1()(
0
)()1(
,,
v
nn
v
nn
v
n
v
n
yxhfyxhfbyy , ,...2,1
v .
Определим v-е приближение для производной
)(
n
xyh
по формуле
)1()(
,
v
nn
v
n
yxhfyh ,
(8.9)
погрешность этого приближения для )(
n
xyh
имеет порядок )(
2k
hO . Тогда
)()(
0
)()1(
,
v
n
v
nn
v
n
v
n
yhyxhfbyy
, ,...2,1
v .
Вычтем (8.7)
из (8.8) при v = 0:
(1) (0) (0)
011
1
(0) (0)
1
01
00
1
() (,)
()
(, ) .
k
nn iini nn n
i
k
ii
nnn nin
i
yy Ayhbfxy hBf
A
B
ybhfxy yhf
bb
(8.10)
Обозначим
0
)( bA
iii
,
011
bB
и определим начальное прибли-
жение для производной
)(
n
xyh
по формуле
k
i
ninin
fhyyh
1
11
)0(
.
(8.11)

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
119
Погрешность этого приближения к )(
n
xyh
имеет порядок )(
1k
hO . Тогда
(8.10)
примет вид
)0()0(
0
)0()1(
,
nnnnn
yhyxhfbyy
.
(8.12)
Из (8.12)
следует, что формула
)()(
0
)()1(
,
v
n
v
nn
v
n
v
n
yhyxhfbyy
справедли-
ва также для v = 0. При этом
)0(
n
yh
определяется с помощью (8.11).
Введем в рассмотрение векторы
T
knnnnn
yyyhyY ),...,,,(
11
и
T
knnnnn
xyxyxyhxyxY ))(),...,(),(),(()(
11
.
Первая компонента
n
y вектора
n
Y аппроксимирует )(
n
xy , вторая компо-
нента
n
yh
вектора
n
Y аппроксимирует )(
n
xyh
. Остальные компоненты
ln
y
аппроксимируют значения точного решения
)(
ln
xy
, 1,...,2,1
kl . Определим
также вектор
T
knn
v
n
v
n
v
n
yyyhyY ),...,,,(
11
)()()(
и матрицу
01...000
........
00...100
00...001
...
...
1211
1211
kk
kk
AAABA
D
.
Тогда предсказывающие формулы (8.7)
и (8.11) для решения )(
n
xy и
производной
)(
n
xyh
могут быть представлены в виде следующего векторного
соотношения:
1
)0(
nn
DYY .
(8.13)
Погрешность первой и второй компоненты вектора
)0(
n
Y имеет порядок
)(
1k
hO , а для остальных равна нулю, если )(
inin
xyy
, 1,...,1 ki , и )(
2k
hO ,
если )()(
2
k
inin
hOyxy . Значит,

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ
Лекция 8. Алгоритмы и методы анализа ССУ во временной области в интегрированных САПР
Автоматизированное проектирование средств и систем управления. Курс лекций
120
)()(
1)0(
k
nn
hOYxY .
(8.14)
Из (8.9)
следует, что
)()()()1(
),(
v
n
v
nn
v
n
v
n
yhyxhfyhyh
.
(8.15)
Введем вектор
T
bc )0,...,0,1,(
0
и функцию невязки
)()()(
),()(
v
n
v
nn
v
n
yhyxhfYF
.
(8.16)
Тогда исправляющие формулы (8.9)
и (8.15) для решения )(
n
xy и произ-
водной )(
n
xyh
могут быть представлены в виде
)(
)()()1( v
n
v
n
v
n
YcFYY
.
(8.17)
Погрешность первой компоненты вектора
)1( v
n
Y
имеет порядок )(
1k
hO , по-
грешность второй компоненты –
)(
2k
hO , а для остальных компонент погреш-
ность такая же, как для
)0(
n
Y . Значит,
)()(
1)1(
kv
nn
hOYxY
.
(8.18)
Итерационный процесс (8.7)
, (8.8) сходится к
n
y , если h достаточно ма-
ло. Следовательно, будет сходиться итерационный процесс (8.13)
, (8.17):
n
v
n
YY
)(
и
)()(
1
k
nn
hOYxY .
Определим линейное преобразование Q, которое переводит вектор )(
n
xY
в вектор
)()(
1
k
n
hOxZ , где
T
n
kk
n
nnn
k
xyhxyh
xyhxyxZ
!
)(
,...,
2
)(
),(),()(
)(2
,
т. е.
)()()(
1
k
nn
hOxZxQY ,
