Ченцов С.В. Автоматизированное проектирование средств и систем управления

Подождите немного. Документ загружается.

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

131

При увеличении шага увеличивается погрешность аппроксимации

кроме того, метод может выйти за границу устойчивости. При уменьшении

шага увеличивается время расчёта. Оптимальную величину шага интегриро-

вания нельзя определить априорно, при этом имеется хороший способ для

выбора величины шага, используемый в любой практической программе ана-

лиза динамических режимов. Шаг интегрирования выбирается так, чтобы

суммарная погрешность была распределена примерно одинаково по шагам.

Исходя из этого, шаг интегрировани

я выбирают в зависимости от заданной

погрешности аппроксимации

, допустимой на один шаг интегрирования

(при этом нужно гарантировать устойчивость вычислений). Для ограниченно

устойчивых методов интегрирования шаг выбирается исходя из условия со-

хранения устойчивости (при этом нужно гарантировать заданную точность

интегрирования). Следовательно, минимизация затрат машинного времени

при соблюдении точностных ограничений возможна только в условиях ин-

тегрирования с переменным шагом.

Большинство алгоритмов автоматического выбора шаг

а основано на

контроле полной ошибки интегрирования, который может быть осуществлён

методом двойного счета, т. е. сравнением результатов

1



, получен-

ных одним полным шагом h и двумя половинными – h/2. Если

доп















, то требования точности удовлетворены. Недостато-

ком является увеличение времени расчёта в два раза. Используется лишь в

явных методах.

Для неявных методов для контроля ошибки используют процесс реше-

ния ОДУ относительно V

k+1

по разности

)0(

11 











между спрогнози-

рованным и окончательным решением.

По количеству итераций р, необходимо для получения Vk + 1(p) такого,

что

() ( 1)

111доп

kkk



  



.

В неявных методах чаще всего используют следующий алгоритм изме-

нения шага. Назначаются оценки

 и

max

 , тогда



нов ст



при

maxmi

 ,

нов ст

hh

при

 ,

нов ст

hh

при

max



ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

132

Конкретное соотношение между

нов ст

зависит от способа кон-

троля полной ошибки. Если контроль выполняется вторым способом – пря-

мым, где ошибка шага характеризуется непосредственно, то новый шаг вы-

числяется по формуле



доп

нов cт











,



доп min



, если







доп max



, если

max1







Если контроль ошибки выполняется косвенным способом, например,

по числу итераций, то используется правило

нов ст



при

maxmi

ppp  ,

нов ст

hch





при

0)(lim





ст

нов



при

max

pp 

с – коэффициент изменения шага, обычно с = 2.

Значение р

min

, р

max

зависят от алгоритма расчета V

k+1

. Для алгоритма

Ньютона р

min

= 2  3; р

max

= 5  6.

Ограничения на максимальный шаг интегрирования может задаваться,

исходя из особенностей решения конкретной задачи, так, чтобы не пропус-

тить быстрых изменений решения V(t). В неявных методах вводится ограни-

чение на минимальный шаг, чтобы в случае невозможности обеспечить за-

данную локальную точность ограничить процесс уменьшения шага и при

min

hh 

выдать соответствующую информацию.

Рассмотрим алгоритмы автоматического выбора шага для одношаго-

вых методов [5

; 12].

1. Алгоритм выбора с помощью удвоения и деления шага пополам

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

133

Пусть





– оценка локальной погрешности метода на шаге h, допу-

щенной при вычислении приближенного значения решения



в точке x

h. Если оценка превосходит некоторую наперед заданную границу











то считается, что значение



решения не удовлетворяет предписанной точ-

ности и шаг h объявляется неприемлемым. Полученная точка x

+h и значение



исключаются из рассмотрения. Выбирается новое значение шага

(1)

/2hh

и вновь по той же формуле с шагом h

(1)

вычисляется новое значение решения

(1)



в новой точке х

+ h

(1)

Пусть

(1)





– оценка локальной погрешности метода на данном шаге

(1)

. Если оценка опять превосходит заданную границу



(1)









то точка х

+ h и значение

(1)



опять исключаются из рассмотрения, шаг сно-

ва делится пополам:

(2) (1)

/2hh

и вычисления повторяются. Так происходит до тех пор, пока при какой-то

величине шага (обозначим ее через h

) оценка локальной погрешности не

станет меньше











После этого считается, что решение дифференциального уравнения

продолжено до точки x

n+1

. Дальнейшее интегрирование уравнения

производится из точки х

n+1

с шагом h

n+1

, который выбирается описанным ни-

же способом.

Если оценка локальной погрешности на шаге h

= x

n+1

-х

удовлетворяет

неравенству







где K – некоторая константа, то считается, что достигнута точность, превы-

шающая заданную, и шаг интегрирования удваивается:

n+l

=2h

. .

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

134

Если выполняется неравенство









то считается, что полученное в точке х

n+1

решение удовлетворяет заданной

точности и шаг интегрирования остается без изменения h

n+l

= h

Таким образом, на тех участках изменения независимой переменной,

где достигается высокая точность приближенного решения, шаг интегриро-

вания возрастает, а там, где точность не достигается, шаг интегрирования со-

кращается до необходимых для ее достижения значений. Тем самым обеспе-

чивается выбор величины шага в зависимости от характера поведения реше-

ния дифференциального уравнения. Константа K обычно полагает

ся равной

2v, где v – порядок используемой оценки локальной погрешности метода.

Иногда для того, чтобы сократить число неприемлемых шагов, в изло-

женный здесь алгоритм выбора шага вносится изменение, которое заключа-

ется в следующем. Если при продолжении решения из точки х

в точку

n+1

= x

+ h

шаг интегрирования сокращался хотя бы один раз, то при выбо-

ре следующего значения шага h

n+1

удвоения предыдущего шага h

не проис-

ходит.

2. Алгоритм выбора максимальной для заданной точности длины шага

Так как оценка





локальной погрешности метода равна с точностью

до членов более высокого порядка малости главному члену локальной по-

грешности метода, то

(, ) .

nnn









(9.4)

Соотношение (9.4)

справедливо для всех оценок. Если оценка





по-

грешности превосходит заданную границу











то считается, что на данном шаге h метод не достигает требуемой точности и

вычисленное значение у

n+1

решения вместе с точкой xn+h исключается из

рассмотрения. В этом случае выбирается новый размер шага, но не последо-

вательным делением пополам, как в описанном выше способе, а с помощью

соотношения









(9.5)

где  находится из условия выполнения равенства

(, )

xyh













(9.6)

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

135

Из (9.4), (9.5) получаем, что





















. Здесь < 1

и новое значение шага













меньше предыдущего. Далее по формуле Рунге – Кутты из точки х

выполня-

ется один шаг h



и вычисляется приближение





к решению дифференци-

ального уравнения в точке x



Если первоначальная оценка



n+1

локальной погрешности метода не

превосходит заданную границу











то считается, что полученное приближение у

n+1

к решению удовлетворяет

требуемой точности и значение x

n+h

независимой переменной принимается

в качестве следующего узла интервала интегрирования. Дальнейшее интег-

рирование уравнения осуществляется из точки х

n+1

с шагом h



. Теперь



 1

и h



 h.

Преимущество данного алгоритма выбора шага заключается в большей

гибкости по сравнению с описанным в предыдущем разделе способом. В нем

при достижении требуемой точности абсолютная величина шага интегриро-

вания либо увеличивается в два раза, либо не изменяется в зависимости от

того, выполняется или нет неравенство







. Если это неравенство

не выполняется из-за незначительного превышения оценки

1n



над величи-

ной



/К, то шаг интегрирования не увеличивается и остается прежним. В ал-

горитме, основанном на использовании формулы (9.5)

, имеется возможность

увеличения шага в любое число



раз даже тогда, когда даннон число мень-

ше двух. Это приводит к более сглаженному изменению шага интегрирова-

ния и, как следствие, к сокращению общего количества шагов и снижению

вычислительных затрат.

В действительности берется несколько меньшее, чем определяемое

значение α, например,

0, 9 0, 9 .













ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

136

И, соответственно, меньшее по сравнению с (9.6) значение шага интегриро-

вания









(9.7)

Это делается для того, чтобы избежать тех шагов, для которых не дос-

тигается требуемая точность.

Как и для одношаговых методов, вопрос о выборе шага интегрирова-

ния для многошаговых методов имеет существенное значение, поскольку от

него зависит не только точность вычисления решения, но и время, необходи-

мое для решения задачи. Имея оценки для ло

кальной погрешности, можно

организовать для многошаговых методов автоматический выбор шага интег-

рирования, руководствуясь теми же соображениями, что и для одношаговых

методов. Однако использование конечно-разностных схем вносит свою осо-

бенность в этот процесс.

Применение переменного шага интегрирования позволяет учитывать

характер поведения решения и уменьшить общее число шагов, сохранив при

этом требуемую точность приближенного решения. Тем самым могут быть

снижены объем работы и машинное время и за

медлен рост вычислительной

погрешности.

Оценка погрешности и автоматический выбор шага и порядка для

метода Гира решения жестких систем. Первые две компоненты вектора

Y равны первым двум компонентам вектора

Z , так как преобразование Q

не меняет первые две компоненты. Следовательно, для оценки погрешности

первой компоненты

y решения

Z уравнения можно воспользоваться оцен-

кой локальной погрешности формулы

)()(

2)1(1







hOxyhC



,

(9.8)

где









Неизвестной величиной в (9.8)

является )(

)1(



. Если заменить про-

изводную )(

)1(

xhy



разностью назад )(

)(



, то при этом допустим по-

грешность порядка

)(

hO . Если заменить )(

)1(1

xyh



на разность

))((

)()(

xyh , то допущена ошибка порядка

)(

2k

)())(()(

2)()1(1 







hOxyhxyh .

Конечную разность

))((

)()(

xyh можно получить, если из последней

компоненты

1, kn

Z вектора

Z вычесть последнюю компоненту

1,1  kn

Z вектора

1n

Z и полученную разность умножить на k!. Следовательно,

!)(

)1(1

kZxyh

knn











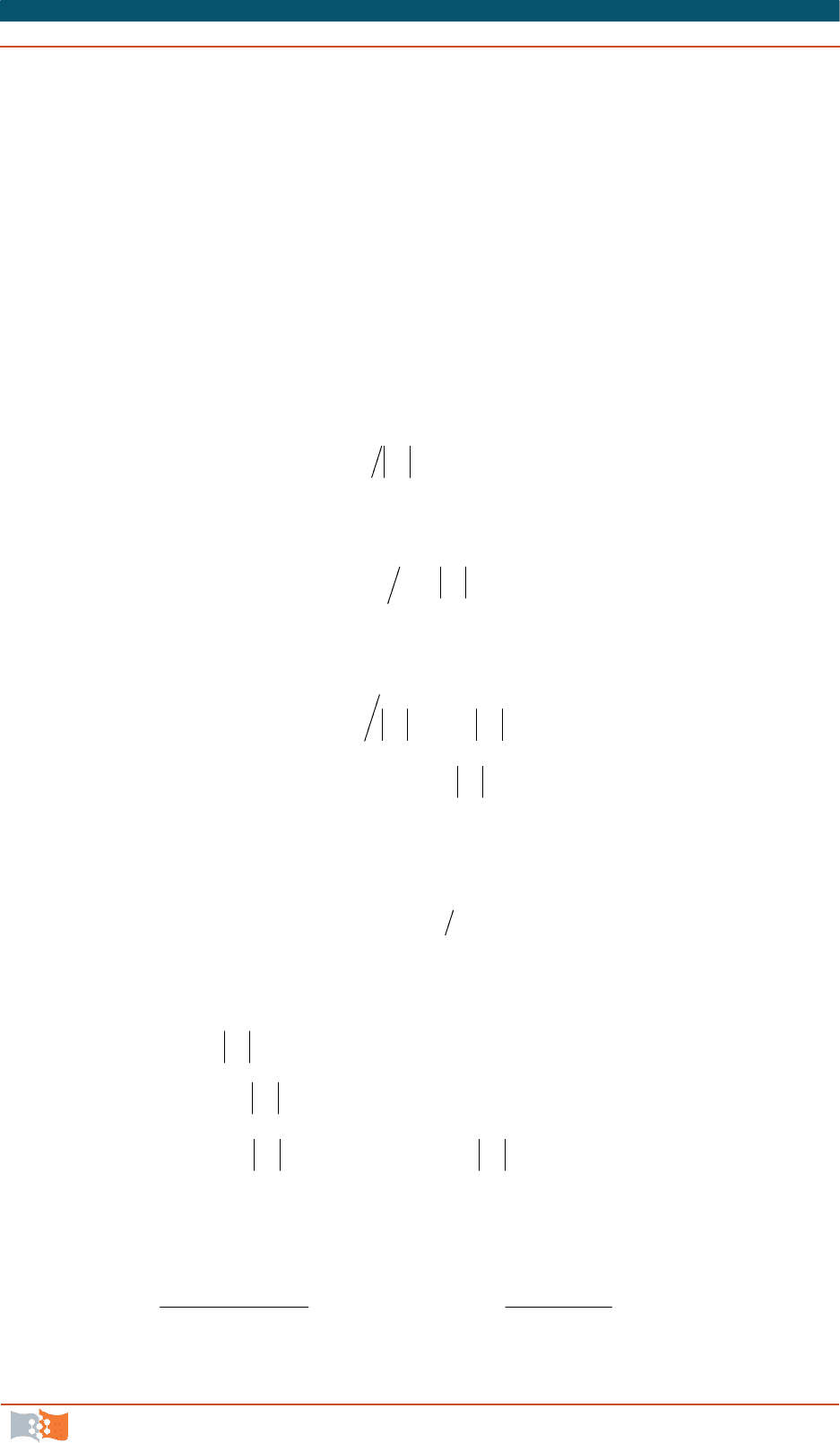
ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

137

В результате имеем

1,1

knkn











(9.9)

или, расписывая покомпонентно,

kZC







Mi ,...,2,1



Последняя компонента вектора

1n

совпадает с последней компонен-

той вектора

)0(

1n



– абсолютная погрешность

. Введены также другие

характеристики точности:

относительная погрешность



0

стандартная погрешность

0

max



мера погрешности

















pyесли

pyеслиy





Все перечисленные характеристики точности можно записывать в об-

щем виде



где

















.,1,

max

ипогрешностмерыдляyиначетоpyесли

ипогрешностйстандартнодляy

ипогрешностнойотносительдляy

ипогрешностабсолютнойдля

Контроль точности ведется по норме









































knn

kZС

1,1



(9.10)

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

138

Тогда



















где



– заданная точность вычисления приближенного решения, и























Тогда, если

EV 

,

то считается, что на данном шаге метод не достигает требуемой точности и

вычисленное значение вместе с точкой исключаются из рассмотрения. Новый

размер шага:





где величина  выбирается так, чтобы на шаге h

достигалась требуемая точ-

ность. Это приводит к следующему значению для :























(9.11)

Вместо (9.11)

можно взять несколько меньшее значение



2.1



















Теперь вычисление можно повторить по формулам (8.24)

, исходя из

точки x

n–1

. Для этого необходимо пересчитать вектор Z

n–1

. Новые значения

компонент этого вектора





n

вычисляются по простым формулам:

,1 







, 1,...,1





Гир вместе с автоматическим выбором шага решает вопрос об автома-

тическом выборе порядка точности метода. Решение в точке х

было получе-

но не методом порядка k, а методом порядка на единицу меньше k–1. Тогда

локальная погрешность решения равна

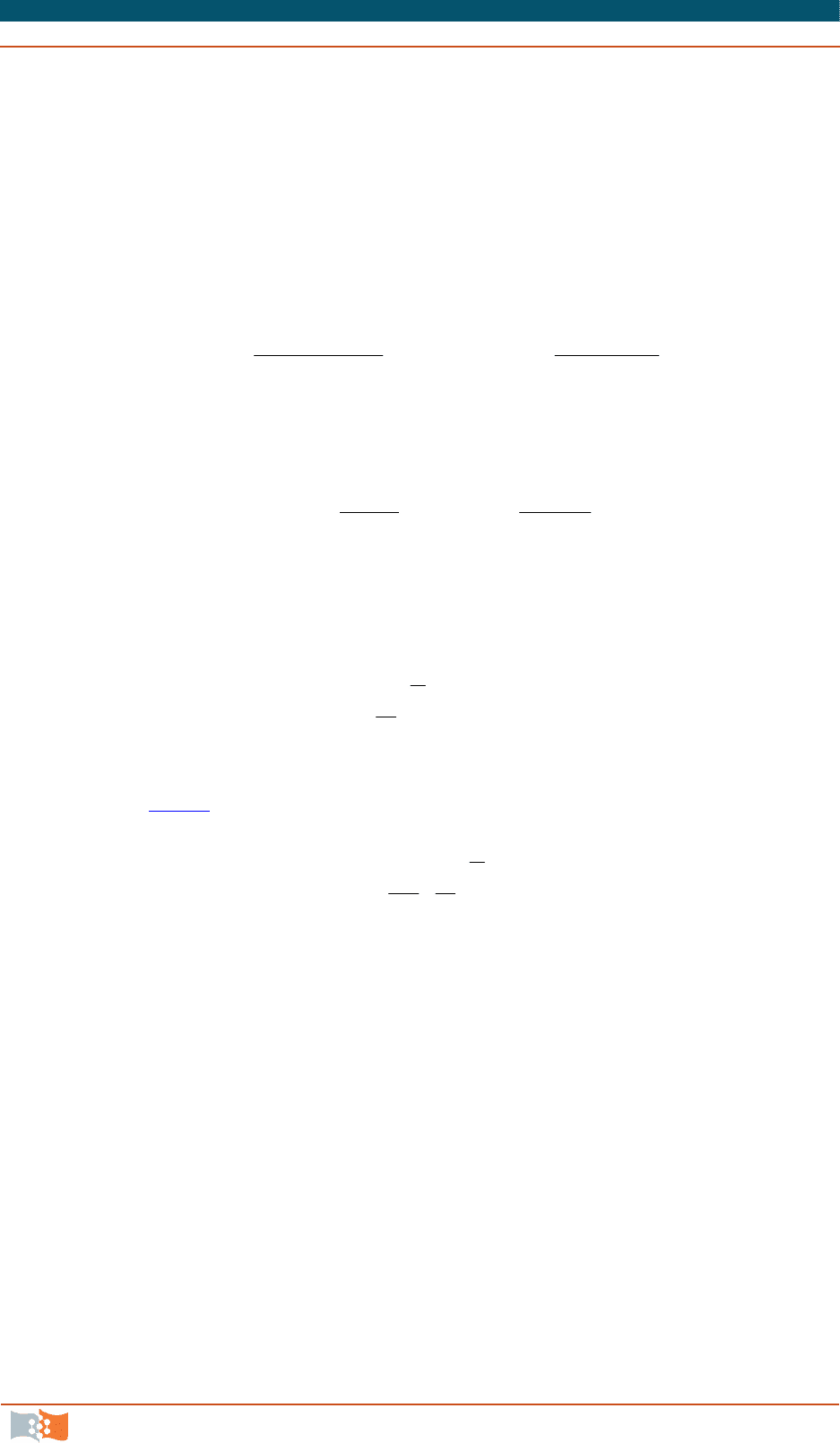
ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

139

)()(

1)( 





hOxyhC



или

kZC











Норма для погрешности запишется в следующем виде:







































knk

kZС

Обозначим













































Если провести все рассуждения аналогично тому, как это было сделано для

метода k-го порядка, то получим аналогичное выражение для константы из-

менения шага в методе порядка k–1:



















.

(9.12)

Вместо (9.12)

можно взять несколько меньшее значение

3.1



















Теперь рассмотрим, как следовало бы изменить шаг интегрирования,

если бы решение в точке было получено методом порядка на единицу боль-

ше. В этом случае погрешность решения была бы равна

)()(

3)2(2







hOxyhC



Выразим

)(

)2(2

xyh



через разность





)()()(

3)(2)2(2 







hOxyhxyh .













1,1,1,

!!!))((

















knknknn

ZkkZkZxyh .

ТЕМА 4. МЕТОДЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ: МЕТОДЫ АНАЛИЗА ССУ

Лекция 9. Параметры оценки эффективности методов анализа во временной области



Автоматизированное проектирование средств и систем управления. Курс лекций

140

В результате имеем

!)(

1,2

kZC

knkn 







.

(9.13)

Норма для погрешности запишется в виде









































knn

kZС

1,2

Обозначим













































Аналогично предыдущему приходим у

значению константы изменения

шага интегрирования в методе порядка k+1

)2(2





















.

(9.14)

Вместо (9.14)

можно взять несколько меньшее значение

)2(2

4.1





















.

(9.15)

Выбором дополнительных множителей в (9.15)

, (9.12) отдается пред-

почтение методу порядка k или k–1.

Для эффективного использования оценки (9.15)

следует при переходе

от точки

1m

к точке

сохранять значение

1,1 



Z , которое используется в

(9.13)

и V.

После вычисления









выбирается тот метод, для которого соот-

ветствующая константа изменения шага максимальна.

Преимущество метода Гира по сравнению с другими многошаговыми

методами численного интегрирования состоит в легкости изменения шага

интегрирования.

Описанная процедура выбора шага и порядка в действительности не-

сколько видоизменяется. Во-первых, если новая предполагаемая длина шага

интегрирования увеличивается менее чем в 1,1 раза по сравнению со ста-

рым значением h, то шаг не изменяется. Во-вторых, изменение шага и по-