Chattaraj P.K. (Ed.) Quantum Trajectories

Подождите немного. Документ загружается.

304 Quantum Trajectories

for the particle. The trajectories x(t) are obtained by integrating this equation with

respect to time and they will lie in a complex x-plane. It was observed that the above

identiﬁcation Ψ = e

S/

helps to utilize all the information contained in Ψ while

obtaining the trajectory. (The dBB approach, which uses Ψ = Re

iS/

does not have

this advantage.)

In view of the above, from here onwards, we consider x as a complex variable.Also

we restrict ourselves to single particles in one dimension for simplicity. The formal

procedure adopted is as follows: Identifying the standard solution Ψ as equivalent

to e

S/

, Equation 19.10 helps us to obtain the expression for the velocity ﬁeld ˙x in the

new scheme. This, in turn, is integrated with respect to time to obtain the complex

trajectory x(t), with an initial position x(0). This complex solution is obviously quite

different from the corresponding dBB solution. The connection with the real physical

world is established by postulating that the physical coordinate or trajectory of the

particle is the real part x

(t)of its complex trajectory x(t). It can be seen that also in this

general case, the modiﬁed dBB trajectory x

(t) is different from the dBB trajectory.

We shall note that this new scheme differs from the dBB also in one important

aspect. Here, when the particle is at some point x in the complex plane, its physical

coordinate is x

and the physical velocity is ˙x

, evaluated at x. Thus for the same

physical coordinate x

, the particle can have different physical velocities, depending

on the point x through which its complex path passes. This in principle rules out the

possibility of ascribing simultaneously well-deﬁned physical position and velocity

variables for the particle [9]. The situation here is very different from that of the dBB

in which for a given physical position of the particle, also the velocity is known, as

obtainable from Equation 19.5. Recently, the prospects of validating the uncertainty

principle using the complex trajectory representation was investigated in Ref. [10].

When

S =

W −Et, where E and t are assumed to be real, the Schrödinger equation

gives us an expression for the energy of the particle

E =

m ˙x

+ V (x) +



∂ ˙x

∂x

. (19.11)

The last term resembles the quantum potential in the dBB theory. However,the concept

of quantum potential is not an integral part of this formalism since the equation of

motion 19.10 adopted here is not based on it.

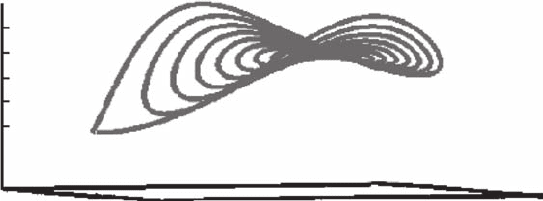
The complex eigentrajectories in the free particle, harmonic oscillator and potential

step problems, and complex trajectories for a wave packet solution were obtained in

Ref. [9]. As an example, complex trajectories in the n = 1 harmonic oscillator are

shown in Figure 19.1.

It is well-known that the QHJE, as given in Equation 19.9, was used by many

physicists such as Wentzel, Pauli, and Dirac, even during the time of inception of

quantum mechanics [11]. In a commendable work in 1982, Leacock and Padgett [12]

have used the QHJE to obtain eigenvalues in many bound state problems, without

actually having to solve the corresponding Schrödinger equation. This method was

further developed by Bhalla, Kapoor, and Panigrahi [13]. However, there were no

trajectories in their works; it is incorrect to ascribe complex quantum trajectories

Modiﬁed de Broglian Mechanics 305

0.8

0.4

–0.4

–0.8

–2 –1 0 1

FIGURE 19.1 The complex trajectories for the n = 1 harmonic oscillator. (Reproduced with

permission from John, M. V., Found. Phys. Lett., 15, 329, 2002.)

to [12], as is done by some authors. It was the work in [9] which, by modifying the

de Broglian mechanics, provided the complex trajectory representation [14,15].

This formalism was extended to three-dimensional problems, such as the hydro-

gen atom, by Yang [16] and was used to investigate one-dimensional scattering prob-

lems and bound state problems by Chou and Wyatt [17,18]. Later,a complex trajectory

approach for solving the QHJE was developed by Tannor and co-workers [19]. Sanz

and Miret-Artés found the complex trajectory representation useful in better under-

standing the nonlocality in quantum mechanics [20].

19.3 PROBABILITY FROM THE VELOCITY FIELD

Instead of computing the complex trajectories x(t), the complex paths x

)inthe

present scheme can directly be found by integrating the equation

˙x

. (19.12)

For doing this integration, Equation 19.10 shall be used. We may note that even for

an eigenstate, the particle can be in any one of its inﬁnitely many possible quantum

trajectories, depending on its initial position in the complex plane. Therefore, the

expectation values of dynamical variables are to be evaluated over an ensemble of

particles in all possible trajectories. It was postulated that the average of a dynamical

variable O can be obtained using the measure Ψ



Ψ as

O=



∞

−∞

OΨ



Ψ dx, (19.13)

306 Quantum Trajectories

where the integral is to be taken along the real axis [9]. Also it was noted that in this

form, there is no need to make the conventional operator replacements. The above

postulate is equivalent to Born’s probability axiom for observables such as position,

momentum, energy, etc., and one can show that Ocoincides with the corresponding

quantum mechanical expectation values. This makes the new scheme equivalent to

standard quantum mechanics when averages of dynamical variables are computed.

However, one of the challenges before this complex quantum trajectory represen-

tation is to explain the quantum probability axiom. In the dBB approach, there were

several attempts to obtain the Ψ



Ψ probability distribution from more fundamental

assumptions [21]. In a recent publication which explores the connection between

probability and complex quantum trajectories [22], the probability density to ﬁnd the

particle around some point on the real axis x = x

was proposed to be



Ψ(x

,0)≡ P (x

) = N exp



−





˙x



, (19.14)

where the integral is taken along the real line. This expression can be veriﬁed by

direct differentiation of |Ψ|

. Since it is deﬁned and used only along the real axis, the

conservation equation for probability in standard quantum mechanics is valid here

also, without any modiﬁcations. This possibility of regaining the quantum probability

distribution from the velocity ﬁeld is a unique feature of the complex trajectory

formulation. For instance, in the dBB approach, the velocity ﬁelds for all bound

eigenstates are zero everywhere and it is not possible to obtain a relation between

velocity and probability.

At the same time, since we have complex paths, it would be natural to consider

the probability for the particle to be in a particular path. In addition, we may consider

the probability to ﬁnd the particle around different points in the same path, which can

also be different. Thus it is desirable to extend the probability axiom to the x

-plane

and look for the probability of a particle to be in an area dx

around some point

, x

) in the complex plane. Let this quantity be denoted as ρ(x

, x

)dx

It is natural to expect that such an extended probability density agrees with Born’s

rule along the real line. We impose such a boundary condition for ρ(x

, x

). Also, it is

necessary to see whether probability conservation holds everywhere in the x

-plane.

It is ideal if we have an expression for ρ(x

, x

), which satisﬁes these two conditions.

Such an extended probability density was proposed in Ref. [22] and showed, with

the aid of the Schrödinger equation, that the conservation equation follows from it.

First, it was postulated that if ρ

, the extended probability density at some point

, x

), is given, then ρ(x

, x

) at another point that lies on the trajectory which

passes through (x

, x

), is

ρ(x

, x

) = ρ

exp



−4







m ˙x

+ V (x)







. (19.15)

Here, the integral is taken along the trajectory [x



), x



)]. The continuity equation

was shown to follow from this axiom by using the extended version of the Schrödinger

equation, which gives

Modiﬁed de Broglian Mechanics 307

Im(E) = Im



m ˙x

+ V (x) +



∂ ˙x

∂x



= 0, (19.16)

since energy and time are assumed real [9,22]. This helps to write the above deﬁnition

Equation 19.15 as

ρ(x

, x

) = ρ

exp



−2



∂ ˙x

∂x





, (19.17)

which in turn gives

dρ

=−2

∂ ˙x

∂x

ρ =−



∂ ˙x

∂x

∂ ˙x

∂x



ρ. (19.18)

The last step follows from the analyticity of ˙x. This leads to the desired continuity

equation for the particle, as it moves along: i.e.,

∂ρ

∂t

∂(ρ ˙x

)

∂x

∂(ρ ˙x

)

∂x

= 0. (19.19)

While evaluating ρ with the help of Equation 19.15 above, one needs to know ρ

, x

) and if we choose this point as (x

, 0), the point of crossing of the trajectory on

the real line, then ρ

may take the value P (x

) and may be found using Equation 19.14.

To summarize, the proposal in Ref. [22] was that the conserved, extended proba-

bility density is

ρ(x

, x

) ∝ exp



−





˙x



exp



−4







m ˙x

+ V (x)







(19.20)

with the integral in the ﬁrst factor evaluated over the real line and that in the second

over the trajectory of the particle.

On the other hand, if we solve the conservation Equation 19.19 for time-

independent problems, i.e.,

∂(ρ ˙x

)

∂x

∂(ρ ˙x

)

∂x

= 0, (19.21)

with the given boundary condition, it is possible to show that the two methods

give identical results. To solve this equation, write ρ(x

, x

) = h(x

, x

)f (p), where

h(x

, x

) is some solution of Equation 19.21 and p is some combination of x

and x

whose value remains a constant along its characteristic curves [23]. Substituting this

form of ρ into Equation 19.21, the characteristic curves are obtained by integrating

the equation

˙x

, (19.22)

which is found to be the same as Equation 19.12. This demonstrates the important

property that the characteristic curves for the above conservation equation are identical

to the complex paths of particles in the present quantum trajectory representation.

308 Quantum Trajectories

We may now ﬁnd the exact form of f (p) by requiring that ρ(x

, 0) agrees with

the probability P (x

), which is the boundary condition in this case. Let the integra-

tion constant in the above Equation 19.22 be the (real) coordinate of any one point

of crossing of the trajectory on the real axis, denoted as x

. Since the characteristic

curves are identical to the complex paths, one can take x

as the constant p along the

characteristic curve and let it be expressed in terms of x

and x

. The assumed form

for the extended probability distribution ρ may then be written as

ρ(x

, x

) = h(x

, x

)f (x

). (19.23)

Now we can choose f (x

) subject to the boundary condition. At the point x = x

at which the curve C crosses the real line, we demand (the boundary condition)

ρ(x

,0)= h(x

,0)f (x

) = P (x

) (19.24)

and obtain f (x

). Expressing x

in terms of x

and x

in f (x

), Equation 19.23

gives ρ(x

, x

Aword of caution is appropriate here.As we shall see below, there may be instances

when the boundary condition overdetermines the problem and we are unable to ﬁnd a

solution. It is observed that this happens in those regions of the complex space where

the complex trajectories do not enclose the poles of x, described as “subnests” in

Ref. [9].

As an example of the proposed scheme, we consider the n = 1 eigenstate of

the harmonic oscillator case, in which one uses Equation 19.14 to regain P (x

) =

exp(−α

). In the next step, h(x

, x

) = (x

) is found to be a solution of

the conservation equation 19.21. f (x

) can now be found as

f (x

) ∝ e

−α

. (19.25)

The complex paths in this case are given by (α

−α

−1)

+4α

= A

constant. Equating this constant to (α

− 1)

, one can obtain f (x

) and also the

extended probability density ρ, in terms of x

and x

. But while taking square roots,

one needs to be careful. It should be noted that for the region containing the subnests

in the harmonic oscillator (with A<1 in the present n = 1 case), the boundary

condition overdetermines the problem, resulting in there being no solution. But for

the region outside it, one can write

f (x

) ∝ exp(−



(α

− α

− 1)

+ 4α

), (19.26)

and therefore,

ρ(x

, x

) ∝ (x

+ x

) exp(−



(α

− α

− 1)

+ 4α

) (19.27)

which is plotted in Figure 19.2. It can be seen that the alternative form of ρ(x

, x

in terms of the trajectory integral Equation 19.20, agrees with the solution of this

equation everywhere in the complex plane.

It is interesting to note that for constant potentials and for the harmonic oscillator,

ρ varies as |˙x|

−2

, as the particle moves along a particular trajectory. This result is not

contradictory to the WKB result that Ψ



Ψ ∝ 1/v

classical

for constant potentials [24],

since |˙x| along a trajectory in our case is not the same as v

classical

Modiﬁed de Broglian Mechanics 309

0.8

0.6

0.4

0.2

–1

–2

–3

–2

–1

FIGURE 19.2 The extended probability density ρ(x

, x

) for the n = 1 harmonic oscillator.

Here, however, there does not exist a conserved probability for the subnests with A<1inthe

interior region. (Reproduced with permission from John, M. V., Ann. Phys., 324, 220, 2009.)

19.4 PROBABILITY DISTRIBUTION FOR THE SUBNESTS

As mentioned above, Equation 19.15 gives a conserved probability along any tra-

jectory in the x

-plane. But we have required that the extended probability agrees

with the Ψ



Ψ probability along the real line. It is seen that such an agreement is not

possible for those trajectories which do not enclose the poles of ˙x. In the context of

solving the conservation equation, it is easy to see that this is due to the boundary

condition overdetermining the problem. In the trajectory integral approach, one can

explain it as a disagreement of the values of ρ at two consecutive points of crossing

of the trajectory on the real axis, with that prescribed by Born’s rule; i.e., as a particle

trajectory is traversed, if the probability ρ at one point of crossing x

on the real axis

agrees with P (x

), then at the other point, say the point x

where the trajectory again

crosses the real line, the probability calculated according to Equation 19.15 will be

different from that of P (x

Given this situation, one can ask whether it is possible to ﬁnd a trajectory integral

deﬁnition for ρ that can agree with Born’s rule (on the real line) in this region, even

if it is not conserved in the extended region. Such a deﬁnition may be found similar

to that in Equation 19.20:

ρ(x

, x

) ∝ exp



−





˙x



exp



−4







m ˙x







. (19.28)

Again the integral in the ﬁrst factor is evaluated over the real line and that in the second,

over the trajectory of the particle. The difference with the deﬁnition Equation 19.20 is

the absence of the potential term V (x) in the integrand in the second factor. However,

for particles moving in zero potential regions, the two deﬁnitions coincide. We plot

the extended probability density for the n = 1 harmonic oscillator in this region in

Figure 19.3.

The probability in this region is substantially high, when compared to that in the

A>1 region. If this is a general feature for all subnests for large n too, it may

310 Quantum Trajectories

0.2

0.1

0.0

FIGURE 19.3 The extended probability density ρ(x

, x

) for the A<1 region of the n = 1

harmonic oscillator, evaluated along the trajectories. This probability density does not obey

the continuity equation, but it agrees with the Born rule along the real line.

explain how the particles are conﬁned close to the real line in the classical limit. It

may also be noted that since the extended probability for A>1 decreases rapidly for

all |x|→∞, there is no difﬁculty in normalizing it for the extended plane.

19.5 DISCUSSION

In classical wave optics, the square of the amplitude is taken as proportional to the

intensity of radiation. While explaining the photoelectric effect, Einstein has ascribed

a certain particle nature to photons. Born remarked thus on the origin of his |Ψ|

—

probability axiom for material particles, in his Nobel lecture: “...anidea of Einstein

gave me the lead. He had tried to make the duality of particles—light quanta or

photons—and waves comprehensible by interpreting the square of the optical wave

amplitudes as a probability density for the occurrence of photons. This concept could

at once be carried over to the ψ-function: |ψ|

ought to represent the probability

density for electrons (or other particles). It was easy to assert this, but how could it be

proved?” [25]. The proof Born thought of was phenomenological, based on atomic

collision processes. Ever since, Born’s probability remained miraculously successful

in all microscopic phenomena, though as an axiom.

In this chapter we have attempted to show that the modiﬁed de Broglian mechanics,

which leads to complex trajectories, is capable of explaining the quantum probability

as originating from dynamics itself. It is seen that both the Born probability along the

real line and the extended probability in the x

-plane are obtainable in terms of cer-

tain line integrals. In the extended case, a conserved probability, which agrees with the

boundary condition (Born’s rule) along the real axis, is found to exist in most regions.

The trajectory integral in this case is over the imaginary part of (1/2)m ˙x

+ V (x).

For other regions (such as the subnests in the n = 1 harmonic oscillator case), an

alternative deﬁnition for the probability satisﬁes the boundary condition on the real

axis, though it is not a conserved one. The integrand here is simply (1/2)m ˙x

. Since

the latter is deﬁned only for the subnests which do not enclose the poles of ˙x, there is

no difﬁculty in normalizing the combined probability for the entire extended plane.

Modiﬁed de Broglian Mechanics 311

There were some other proposals for computing probability in the extended

complex plane. One such attempt [26] is to deﬁne ρ(x) =

Ψ(x)Ψ(x) where

Ψ(x) ≡



), with x complex. The complexiﬁed ﬂux is chosen as j(x, t ) = v(x, t )ρ(x, t ) =

−(i/m)Ψ



)Ψ



where v(x, t) ≡˙x is given by Equation 19.10 and the prime denotes

spatial differentiation. With the help of the time-dependent Schrödinger equation, the

author shows that, in general, ∂ρ/∂t = j



(x, t ). This arguably leads to nonconserva-

tion of probability along trajectories. But we should remember that this negative result

is based on the choices made in [26] for the probability density and ﬂux. Moreover,

this deﬁnition leads to a complex probability off the real axis, which is undesirable.

Another approach is to deﬁne the probability as Ψ



(x)Ψ(x) itself [27,28]. Though this

has the advantage of being real everywhere, it is not shown to obey any continuity

equation anywhere. Nor is it generally a normalizable probability in the extended

plane.

Notwithstanding a host of other issues to be solved for the new mechanics, the fact

that it can account for Born’s rule in terms of the velocity ﬁeld raises our hopes for a

deeper understanding of quantum probability.

BIBLIOGRAPHY

1. H. Goldstein, Classical Mechanics, Addison-Wesley, Reading, MA, 1980.

2. L. de Broglie, Ph.D. Thesis, University of Paris, 1924.

3. L. de Broglie, J. Phys. Rad., 6

serie, t. 8, (1927) 225.

4. G. Bacciagaluppi, A. Valentini, Quantum Theory at the Crossroads, Cambridge University

Press, Cambridge, 2009; quant-ph/0609184v1 (2006).

5. D. Bohm, Phys. Rev. 85 (2), 166 (1952) 180.

6. E.R. Floyd, Phys. Rev. D 26 (1982) 1339.

7. A. Faraggi, M. Matone, Phys. Lett. B 450 (1999) 34.

8. R. Carroll, J. Can. Phys. 77 (1999) 319.

9. M.V. John, Found. Phys. Lett. 15 (2002) 329; quant-ph/0102087 (2001).

10. C.D. Yang, Phys. Lett. A 372 (2008) 6240.

11. G. Wentzel, Z. Phys. 38 (1926) 518; W. Pauli, in: H. Geiger, K. Scheel (Ed.), Handbuch

der Physik, 2nd ed., Vol. 24, part 1, Springer-Verlag, Berlin, 1933, pp. 83–272; P.A.M.

Dirac, The Principles of Quantum Mechanics, Oxford University Press, London, 1958.

12. R.A. Leacock, M.J. Padgett, Phys. Rev. Lett. 50 (1983) 3; R.A. Leacock, M.J. Padgett,

Phys. Rev. D 28, (1983) 2491.

13. R.S. Bhalla, A.K. Kapoor, P.K. Panigrahi, Am. J. Phys. 65 (1997) 1187; R.S. Bhalla,

A.K. Kapoor, P.K. Panigrahi, Mod. Phys. Lett. A 12 (1997) 295.

14. A.S. Sanz, S. Miret-Artés, J. Chem. Phys. 127 (2007) 197101.

15. Y. Goldfarb, I. Degani, D.J. Tannor, J. Chem. Phys. 127 (2007) 197102.

16. C.-D. Yang, Ann. Phys. (N.Y.) 319 (2005) 339; C.-D. Yang, Int. J. Quantum Chem. 106

(2006) 1620; C.-D. Yang, Ann. Phys. (N.Y.) 319 (2005) 444; C.-D. Yang, Chaos, Solitons

Fractals 30 (2006) 342.

17. C.-C. Chou, R.E. Wyatt, Phys. Rev. E 74 (2006) 066702; C.-C. Chou, R.E. Wyatt, J. Chem.

Phys. 125 (2007) 174103.

18. R.E. Wyatt, Quantum Dynamics with Trajectories: Introduction to Quantum Hydrody-

namics, Springer, New York, 2005.

19. Y. Goldfarb, I. Degani, D.J. Tannor, J. Chem. Phys. 125 (2006) 231103.

312 Quantum Trajectories

20. A.S. Sanz, S. Miret-Artés, Chem. Phys. Lett. 445 (2007) 350.

21. D. Bohm, B.J. Hiley, The Undivided Universe, Routledge, London and New York, 1993;

P. Holland, The Quantum Theory of Motion, Cambridge University Press, Cambridge,

1993.

22. M.V. John, Ann. Phys. 324 (2009) 220; arXiv:0809.5101 (2008).

23. K.F. Riley, M.P. Hobson, S.J. Bence, Mathematical Methods for Physics and Engineering,

Cambridge University Press, Cambridge, 1997, p. 526.

24. J.J. Sakurai, Modern Quantum Mechanics, Addison Wesley Longman, Singapore, 1994

p. 104.

25. M. Born, Nobel lecture, 1954.

26. B. Poirier, Phys. Rev. A 77 (2008) 022114.

27. C.C. Chou, R.E. Wyatt, Phys. Lett. A 373 (2009) 1811.

28. C. D. Yang, Chaos, Solitons Fractals 42 (2009) 453.

Types of Trajectory Guided

Grids of Coherent States

for Quantum Propagation

Dmitrii V. Shalashilin

CONTENTS

20.1 Introduction.................................................................................................313

20.2 Theory.........................................................................................................314

20.2.1 Variational Principle......................................................................314

20.2.2 Variational Multiconﬁgurational Gaussians (vMCG)...................315

20.2.3 Variational Single Conﬁgurational Gaussian (vSCG)...................316

20.2.4 Coupled Coherent States (CCS)....................................................317

20.2.5 The Gaussian Multiconﬁgurational Time-Dependent

Hartree Method.............................................................................318

20.2.6 The Ehrenfest Method...................................................................318

20.2.7 The Multiconﬁgurational Ehrenfest Method ................................319

20.3 Conclusions.................................................................................................320

Appendix: Variational Principle and the Equations of G-MCTDH .......................320

Bibliography ..........................................................................................................322

20.1 INTRODUCTION

Several methods have been suggested in the literature, which employ various trajec-

tory guided grids of frozen Gaussian wavepackets as a basis set for quantum propa-

gation. They exploit the same idea illustrated in Figure 20.1a, that a grid can follow

the wavefunction. Therefore a basis does not have to cover the whole Hilbert space of

the system, as the one shown in Figure 20.1b. Among the methods considered in this

chapter are the method of variational Multiconﬁgurational Gaussians (vMCG) and the

Gaussian Multiconﬁgurational time-dependent Hartree (G-MCTDH) technique [1],

the method of Coupled Coherent States (CCS) [2] and the recently developed Multi-

conﬁgurational Ehrenfest approach (MCE) [3], which all differ in the exact way their

grids are guided. The goal of this chapter is to present all four techniques from the

same perspective and compare their mathematical structure.

313