Chattaraj P.K. (Ed.) Quantum Trajectories

Подождите немного. Документ загружается.

284 Quantum Trajectories

real-valued quantum trajectories for solving a wide range of quantum mechanical

problems [10].

Quantum trajectories in complex space in the framework of the quantum Hamilton–

Jacobi formalism, developed by Leacock and Padgett in 1983 [11, 12], have recently

attracted signiﬁcant interest. This variant of the Bohmian approach is based on sub-

stitution of the wave function expressed by the complex action function into the time-

dependent Schrödinger equation to obtain the complex-valued QHJE (this version is

not the same as that in Bohm’s formalism). This complex quantum hydrodynamic

representation provides conceptual novelty, and also leads to new trajectory-based

pictures of quantum mechanics that prove useful in computational applications.

For stationary states, an accurate computational method has been proposed for the

complex-valued QHJE to obtain the wave function and the reﬂection and transmis-

sion coefﬁcients for one-dimensional problems [13–15]. For nonstationary states,

the derivative propagation method (DPM) [16] developed in Bohmian mechanics

has also been utilized to obtain approximate complex quantum trajectories and

the wave function for one-dimensional barrier scattering [17–19]. In addition, this

approach has been employed to describe the interference effects and node formation

in the wave function [20, 21], to determine energy eigenvalues [22], and to improve

the complex time-dependent Wentzel–Kramers–Brillouin method [23, 24]. Further-

more, the complex trajectory method has also been employed to analyze complex

quantum trajectories and the complex quantum potential and to calculate tunnel-

ing probabilities for one-dimensional and multi-dimensional wave-packet scattering

problems [25–31].

In the analytical approach, complex quantum trajectories determined from the

known analytical form of the wave function have been analyzed for several stationary

and nonstationary problems, including the free particle, the potential step, the potential

barrier, the harmonic potential, and the hydrogen atom [32–39]. A uniﬁed descrip-

tion for complex quantum trajectories for one-dimensional problems has been pre-

sented [40]. Common features of complex quantum trajectories for one-dimensional

stationary scattering problems have been analyzed for the Eckart and the hyperbolic

tangent barriers [40,41]. In addition, quantum vortices form around a node in the wave

function in complex space, and the discontinuity in the real part of the complex action

leads to the quantized circulation integral [42]. Quantum streamlines near singulari-

ties of the quantum momentum function (QMF) and its Pólya vector ﬁeld (PVF) have

been thoroughly analyzed [43]. Moreover, quantum interference demonstrated by the

head-on collision of two Gaussian wave packets has been explored in the complex

plane [44–46]. On the other hand, several studies have been dedicated to issues related

to the probability density and ﬂux continuity in the complex plane and probability

conservation along complex quantum trajectories [47–50].

In the current study, the equations of motion for complex quantum trajectories for

one-dimensional time-dependent and time-independent problems will be reviewed

in Section 18.2. Several recent analytical studies employing the complex quan-

tum trajectory representation will be described in Section 18.3. Finally, we con-

clude with some comments and various promising topics for future investigations in

Section 18.4.

Analytical Studies of Complex Quantum Trajectories 285

18.2 QUANTUM TRAJECTORIES IN COMPLEX SPACE

18.2.1 TIME-DEPENDENT PROBLEMS

Based on the quantum Hamilton–Jacobi formalism developed by Leacock and Padgett

[11,12], the complex-valued QHJE is readily obtained by substituting the polar form

of the complex-valued wave function,

Ψ(x, t ) = exp





S(x, t)



, (18.1)

into the time-dependent Schrödinger equation to obtain

−

∂S

∂t



∂S

∂x



+ V +



2mi

∂

∂x

, (18.2)

where S(x, t) is the complex action. As in Bohmian mechanics, the QMF is given by

the guidance equation p(x, t) = ∂S(x, t)/∂x. To ﬁnd a quantum trajectory, we may

rearrange this equation as

∂S(x, t)

∂x

. (18.3)

However, since the action S(x, t) is complex-valued and time remains real-valued,

the trajectory requires a complex-valued coordinate. Therefore, the QMF p(x, t) and

the complex action S(x, t) are extended to the complex space by replacing x with z.

Thus, a complex quantum trajectory is deﬁned by

p(z, t)

. (18.4)

In addition, the terms on the right side of Equation 18.2 correspond to the kinetic

energy, the classical potential, and the quantum potential in complex space, respec-

tively. Moreover, the QMF can be expressed in terms of the wave function through

use of Equation 18.1

p(z, t) =



Ψ(z, t)

∂Ψ(z, t)

∂z

. (18.5)

Through Equation 18.2, we can obtain the equations of motion for z(t), p(z, t),

and S(z, t ) for quantum trajectories in the complex space

, (18.6)

∂p

∂z

∂p

∂t

=−

−



2mi

∂

∂z

, (18.7)

∂S

∂z

∂S

∂t

− V −



2mi

∂p

∂z

. (18.8)

286 Quantum Trajectories

The two terms on the right side of Equation 18.7 correspond to the classical force f

−dV(z)/dz and the quantum force f

=−(/2mi)∂

p/∂z

, respectively. Therefore,

we can determine the quantum trajectories of particles in complex space by integrating

these equations and then synthesize the wave function through Equation 18.1.

For time-dependent problems, the initial state Ψ(z, 0) is used to determine the

initial condition (z

, p(z

, 0), S(z

, 0)), where z

is the starting point of the trajec-

tory. It is noted that the integration of Equations 18.6 through 18.8 involves the

spatial derivative for the QMF. The equations of motion are not closed and general

numerical methods for systems of ordinary differential equations cannot be applied

to the integration of the equations of motion for quantum trajectories. However, the

DPM has been developed to overcome a similar difﬁculty in Bohmian mechanics

by solving a truncated system of equations for amplitude, phase and their spatial

derivatives [16]. A computational approach through use of the DPM for solving

the equations of motion in complex space using the iteration of the spatial partial

derivatives of the QMF has been applied to one-dimensional and multi-dimensional

scattering problems. Tannor and collaborators have applied this method, which they

call Bohmian mechanics with complex action (BOMCA), to one-dimensional scat-

tering of an initial Gaussian wave packet from a thick Eckart barrier [17–19]. In

addition, they have employed this approach to describe the interference effects

and node formation in the wave function [20, 21], to determine energy eigenval-

ues [22], and to improve the complex time-dependent Wentzel–Kramers–Brillouin

method [23, 24]. Furthermore, Wyatt and collaborators have utilized this approach

to investigate one-dimensional and multi-dimensional wave-packet scattering prob-

lems [25–31].

Complex quantum trajectories can be obtained for arbitrary initial positions, and

the initial conditions for the quantum trajectories are determined by the initial state.

Namely, a particle can start its motion at any position, and information such as the

complex action is transported along its complex quantum trajectory. At a later time,

when the particle crosses the real axis, we can record the information. Thus, for those

particles which cross the real axis simultaneously, the wave function on the whole real

axis can be synthesized using the information transported by these particles. Because

the correct wave function at a speciﬁc time on the real axis must be determined

by the information transported by particles arriving simultaneously at the real axis, a

curve for the special initial positions of these particles in the complex space is deﬁned

as an isochrone [40]. The concept of isochrones has been analytically demonstrated

by the free Gaussian wave packet and the coherent state in the harmonic potential in

the complex plane [40].

18.2.2 T

IME-INDEPENDENT PROBLEMS

For stationary states with eigenenergy E, the complex action can be expressed by

S(z, t ) = W (z) −Et and the QMF becomes

p(z, t) =

∂S

∂z

dW(z)

= p(z), (18.9)

Analytical Studies of Complex Quantum Trajectories 287

where W (z) is called the quantum characteristic function and p(z) is the stationary

state QMF which depends only on z. Moreover, the stationary state QMF is related

to the stationary state wave function by

p(z) =



ψ(z)

dψ(z)

. (18.10)

Then, using the expression S(z, t) = W (z) − Et and rewriting the QHJE in Equa-

tion 18.2 in terms of the stationary state QMF yield the stationary-state QHJE

p(z)

+ V (z) +



2mi

dp(z)

= E. (18.11)

Similarly, we can obtain the equations of motion for stationary states from Equa-

tions 18.6 through 18.8

, (18.12)





E − V −



p, (18.13)

, (18.14)

where the stationary-state QHJE in Equation 18.11 has been used.

When solving equations of motion for quantum trajectories, we encounter different

difﬁculties for time-dependent and time-independent problems. For time-dependent

problems, the system of equations of motion given in Equations 18.6 through 18.8 is

not closed because the QMF is coupled to its spatial derivative. Therefore, general

numerical methods for differential equations cannot be applied directly. For time-

independent problems, although the system of equations of motion given in Equa-

tions 18.12 through 18.14 is closed, it is evident from Equation 18.10 that only solving

the equations of motion with the correct initial quantum momentum p(z

) can yield

the correct quantum trajectories belonging to the corresponding stationary states.

Moreover, it is found from Equations 18.12 through 18.14 that the quantum char-

acteristic function W (z) is not coupled to z and p. Therefore, we only need to use

Equations 18.12 and 18.13 to solve for quantum trajectories. In summary, the difﬁ-

culty in solving time-dependent problems arises from the integration of the equations

of motion, while the difﬁculty in solving time-independent problems arises from the

speciﬁcation of the initial conditions.

18.3 ANALYTICAL STUDIES OF THE COMPLEX QUANTUM

TRAJECTORY FORMALISM

18.3.1 Q

UANTUM TRAJECTORIES FOR ONE-DIMENSIONAL STATIONARY

SCATTERING PROBLEMS

One-dimensional stationary scattering problems including the Eckart and the hyper-

bolic tangent barriers have been investigated in the framework of the complex

288 Quantum Trajectories

quantum Hamilton–Jacobi formalism [40, 41]. Exact complex quantum trajecto-

ries were determined by numerically integrating the equations of motion in Equa-

tions 18.12 and 18.13 using either forward or backward integrations. In the forward

integration, we used the exact initial condition in the reﬂection region to solve the

equations of motion. In the backward integration, the asymptotic QMF in the trans-

mission region was used as the initial condition to numerically solve the equations

of motion backwards. In addition, the total potential can be calculated from the exact

analytical scattering wave function.

The state-dependent total potential (the sum of the classical and the quantum

potentials) presents unusual and complicated structure in the complex plane. The total

potential displays periodicity along the direction of the imaginary axis and reveals

a complicated channel structure in the reﬂection region. For example, Figure 18.1a

displays the real part of total potential for the one-dimensional scattering problem

with the potential barrier

V (x) = V



1 −



1 − exp(x/a)

1 + c exp(x/a)





. (18.15)

In addition, the quantum potential of one-dimensional scattering problems shows a

second-order pole or four-lobed quadrupole structure in the reﬂection region, and this

structure originates from the asymptotic behavior of the wave function. Although the

classical potentials extended analytically to complex space may show different pole

structures for each problem, the quantum potentials present the same second-order

pole structure in the reﬂection region.

In these studies [40, 41], some particles starting in the reﬂection region pass the

barrier into the transmission region, and some rebound from the barrier back to the

reﬂection region. In addition, localized closed trajectories form around stagnation

points of the QMF in the reﬂection region, and they are imbedded in the walls of

the channel structure. Trajectories may spiral into attractors or out of repellers near

the barrier region. As shown in Figure 18.1b, for the forward integration, some par-

ticles move toward the transmission region, and some move toward the left. For the

backward integration, some trajectories link the reﬂection and transmission regions.

Some trajectories are traced from the transmission region to the repellers in the bar-

rier region. However, some trajectories obtained by the forward integration spiral into

attractors in the barrier region. Furthermore, we also derived the ﬁrst-order and the

second-order equations for local approximate quantum trajectories near stagnation

points of the QMF, and used the ﬁrst derivative of the QMF to describe the forma-

tion of attractors and repellers. Quantum trajectories present similar structures for

one-dimensional stationary scattering problems.

As another example, Figure 18.2 displays quantum trajectories and the quantum

momentum ﬁeld for the hyperbolic tangent potential barrier given by

V (x) =



1 + tanh





. (18.16)

For the energy lower than the barrier height, particles starting from the reﬂection

region may penetrate into the nonclassical region, and then turn back to the reﬂection

Analytical Studies of Complex Quantum Trajectories 289

(a) Re(V

total

)

–5

–10

–5

–4

–2

–10

–7.5 –5 –2.5 0 2.5 5

–3

–2

–1

(b)

FIGURE 18.1 Scattering for the potential barrier in Equation 18.15 with E = 1.2, V

= 1,

and c = 0.5: (a) Real part of the total potential; (b) quantum trajectories obtained by forward

or backward integrations, and the contour map of the real part of the total potential. The initial

positions for the forward integration are shown as dots. Relevant physical quantities are used

in dimensionless units. (Reproduced with permission from Chou, C. C. and Wyatt, R. E.,

J. Chem. Phys., 128, 154106, 2008. Copyright AIP 2008.)

region. The classical turning curve is deﬁned by the curve where the scattering energy

is equal to the real part of the total potential. From the stationary-state QHJE in Equa-

tion 18.11, the sum of the complex-valued kinetic energy, classical potential, and

quantum potential along a complex quantum trajectory is equal to the real-valued

scattering energy. The variations of these energies along complex quantum trajec-

tories were also analyzed. Therefore, these studies not only analyzed common fea-

tures of complex quantum trajectories and total potentials for these examples but

also demonstrated general properties and similar structures of the complex quantum

trajectories and the quantum potentials for one-dimensional time-independent scat-

tering problems [40,41].

290 Quantum Trajectories

–8 –6 –4 –2 0 2

–3

–2

–1

FIGURE 18.2 For the soft potential step in Equation 18.16 with E = 0.6:quantum trajectories

(solid curves), the quantum momentum ﬁeld, and the classical turning curve (dashed curve) in

the principal zone. The initial positions for the forward integration are shown as dots. Relevant

physical quantities are used in dimensionless units. (Reproduced with permission from Chou,

C. C. and Wyatt, R. E., J. Chem. Phys., 128, 154106, 2008. Copyright AIP 2008.)

18.3.2 QUANTUM VORTICES AND STREAMLINES WITHIN THE COMPLEX QUANTUM

HAMILTON–JACOBI FORMALISM

Dirac predicted the formation of quantized vortices around nodes in the wave function

in 1931 [51]. In quantum hydrodynamics in two or more real coordinates, quantum

vortices form around nodes in the wave function and they carry quantized circulation

[52–56]. Streamlines surrounding the vortex core form approximately circular loops.

Such vortices play an important role in a diverse range of physical process such as

the appearance of quantum vortices in quantum wave-packet studies of the collinear

H +H

→ H

+ H exchange reaction [57–59].

Quantum vortices and streamlines in complex space were recently explored within

the quantum Hamilton–Jacobi formalism [42, 43]. A quantum vortex forms around a

node in the wave function in complex space, and the quantized circulation integral

along a simple curve enclosing a node originates from the discontinuity in the real part

of the complex action. The PVF for a complex function was introduced to interpret

the circulation integral [60–62]. Pólya introduced a simple interpretation for complex

contour integrals by associating a complex function f (z) with a vector ﬁeld

f (z). If

f = u + iv, then the associated PVF is given by F = u − iv, and F = (u, −v)is

the conjugate vector ﬁeld to f = (u, v) in the complex plane. The complex integral

of the QMF can be interpreted in terms of the work and ﬂux of its PVF along the

contour. The real valuedness of the quantized circulation integral implies that only

the work term contributes to the quantized circulation integral around a node

p(z)dz =

P · d

 + i

P · d

n = nh, (18.17)

Analytical Studies of Complex Quantum Trajectories 291

where C denotes a simple closed curve in the complex plane,

P = (p

, −p

)is

the PVF, d

 = (dx, dy) is the tangent vector in the direction of the path C, and

n = (dy, −dx) is the normal vector pointing to the right as we travel along C.

Anonstationary state constructed from a linear combination of the ground, ﬁrst, and

second-excited states of the harmonic oscillator was used to illustrate the formation

of a transient excited state quantum vortex.

Ψ(z, t) =

√

(z)e

−iE

t/

− 2ψ

(z)e

−iE

t/

+ ψ

(z)e

−iE

t/

, (18.18)

where this wave function was extended to the complex space. The excited state vor-

tices form around a higher-order node. In this example, two long-lived ground state

vortices collide to form a transient ﬁrst-excited state vortex, and then the ﬁrst-excited

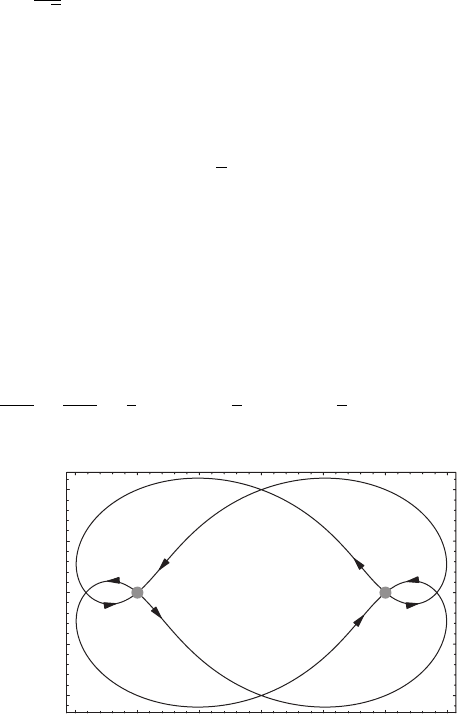
state vortex immediately splits into two ground state vortices! Figure 18.3 shows

the trajectories for the two nodes of the nonstationary state given in Equation 18.18,

where the dimensionless units z

√

αz and t

= ωt have been used. At t = 0,

the wave function has a second-order node at z = 1, and then the second-order node

splits into two ﬁrst-order nodes. At t = π, these two ﬁrst-order nodes collide again

to form a second-order node at z =−1. They separate for π <t<2π and ﬁnally

return to the initial position at z = 1.

The coupled harmonic oscillator was used as an example to present the quan-

tized circulation integral in the multidimensional complex space. The two-particle

Hamiltonian of coupled harmonic oscillators is given by

H =

(

− x

)

. (18.19)

–1.5 –1 –0.5 0 0.5 1 1.5

–1

–0.5

0.5

FIGURE 18.3 The trajectories for the two nodes of the nonstationary state given in Equa-

tion 18.18. At t = 0, these two ﬁrst-order nodes coincide to form a second-order node (the right

dot). At t = π, these two ﬁrst-order nodes coincide again to form a second-order node (the left

dot). When t = 2π, these two nodes return to the initial point. (Reproduced with permission

from Chou, C. C. and Wyatt, R. E., J. Chem. Phys., 128, 234106, 2008. Copyright AIP 2008.)

292 Quantum Trajectories

We consider the exact stationary state

, x

) =





1/4

−



4π



1/4



2α

1/2



−

, (18.20)

where M = m

+ m

, µ = m

/(m

+ m

), α

= Mω/, α

= µ ¯ω/, ¯ω =

(ω

+ k/µ)

1/2

, X = (m

+ m

)/M, and x = x

− x

. Then, we extend the

wave function in Equation 18.20 into the complex space by replacing x

and x

with

and z

. By setting Ψ

, z

) = 0, we obtain the corresponding nodal plane

−z

= 0 in the four-dimensional complex space. Similarly, the circulation integral

along a loop c for this case is given by

Γ =

!p(z

, z

) · d!z =

, z

)dz

, z

)dz

, (18.21)

where the QMF for multidimensional problems is deﬁned by !p =

∇S = (/i)

(

∇Ψ/Ψ).

In order to calculate the circulation integral, we need to choose a closed curve to

“enclose" the two-dimensional nodal plane in the four-dimensional complex space.

The two-dimensional nodal plane is given by z

− z

= 0, and we can ﬁnd a closed

curve in the plane z

= 0 to enclose the nodal plane. The intersection of these two

planes is only the point (z

, z

) = (0, 0). Thus, we use a circle of arbitrary radius R

centered on this point in the plane z

= 0 as the closed loop to enclose the nodal

plane z

− z

= 0. Accordingly, we let z

= Re

iθ

, and then z

=−z

=−Re

iθ

Thus, we evaluate the circulation integral by integrating from θ = 0toθ = 2π

Γ =

, z

)dz

, z

)dz

= π + π = h. (18.22)

The circulation integral is quantized and equal to h. In addition, we note that each

term in Equation 18.22 contributes h/2 to the circulation integral. Therefore, the

circulation integral along a closed curve enclosing the nodal plane in complex space is

quantized.

Local structures of the QMF and its PVF near stagnation points and poles were

thoroughly analyzed, and the equations for approximate quantum streamlines around

these points were also derived [43]. Streamlines near a stagnation point of the QMF

may spiral into or away from it, or they may become circles centered on this point

or straight lines passing through this point. In contrast to Bohmian mechanics in real

space, streamlines near a pole display East-West and North-South opening hyperbolic

structure. On the other hand, streamlines near a stagnation point of the PVF display

general rectangular hyperbolic structure, and streamlines near a pole become circles

enclosing the pole. Although the QMF displays hyperbolic ﬂow near a node, its PVF

displays circular ﬂow around a quantum vortex. Furthermore, the local structures of

the QMF and its PVF around a stagnation point are related to the ﬁrst derivative

of the QMF; however, the magnitude of the local structures for these two ﬁelds near

a pole depends only on the order of the node in the wave function. These studies

Analytical Studies of Complex Quantum Trajectories 293

–1.5 –1 –0.5 0 0.5 1 1.5

–1.5

–1

–0.5

0.5

(a)

–1.5 –1 –0.5 0 0.5 1 1.5

–1.5

–1

–0.5

0.5

(b)

FIGURE 18.4 For t = 1.5: (a) the quantum momentum ﬁeld; (b) the Pólya vector ﬁeld and

contours of the probability density (solid lines) with the stagnation points (small dots) and the

pole (large dot). (Reproduced with permission from Chou, C. C. and Wyatt, R. E., J. Chem.

displayed the rich dynamics of streamlines in complex space for one-dimensional

time-dependent and time-independent problems.

Figure 18.4 presents the QMF and the PVF around stagnation points and poles

for a nonstationary state constructed from a linear combination of the ground and

ﬁrst-excited states of the harmonic oscillator

Ψ(z, t) = ψ

(z)e

−



+ ψ

(z)e

−



. (18.23)

The following dimensionless units are used: z

= z/

√

/mω, p

= p/

√

mω, t

t/(1/ω), and E

= E/ω. In Figure 18.4a, the positive imaginary part of the ﬁrst

derivatives of the QMF at these two stagnation points contributes to counterclockwise

ﬂow of the QMF, and the positive or negative real parts of the ﬁrst derivatives of

the QMF lead to divergence or convergence of the streamlines to the stagnation

points, respectively. In addition, the QMF displays hyperbolic ﬂow around the pole.

In Figure 18.4b, the PVF displays hyperbolic ﬂow around the two stagnation points

and circular ﬂow around the pole. In addition, the PVF is parallel to contours of the

complex-extended Born probability density [42,48].

18.3.3 Q

UANTUM CAVES AND WAVE-PACKET INTERFERENCE

Quantum interference was investigated for the ﬁrst time within the complex quantum

Hamilton–Jacobi formalism [44–46]. The Gaussian wave-packet head-on collision

was used as an example to demonstrate quantum interference in complex space. This

process can be described by the total wave function, Ψ(x, t ) = ψ

(x, t ) + ψ

(x, t )

(L/R denotes left/right). Each partial wave is represented by a free Gaussian wave

packet,

ψ(x, t ) = A

−(x−x

)

/4σ

+ip(x−x

)/+iEt/

, (18.24)

where, for each component, A

=(2πσ

)

−1/4

and the complex time-dependent spread-

ing is given by σ

= σ

(1 + it/2mσ

) with the initial spreading σ

. The total wave