Chattaraj P.K. (Ed.) Quantum Trajectories

Подождите немного. Документ загружается.

254 Quantum Trajectories

Note however that



∂

(

0, x

)

(

0, x

)

= 0

for x =±1.

There are more challenges to Bohmian mechanics. The notion of distributional

solutions to a partial differential equation like Equation 16.1 raises the question of

whether these solutions support a kind of Bohmian particle motion like the classical

solutions do. After all quantum mechanics employs such distributional solutions.

16.3 BOHMIAN EVOLUTION FOR Ψ

∈ C

∞

In standard quantum mechanics the classical solutions, i.e., the C

-solutions of Equa-

tion 16.1, do not represent all physically possible situations. Rather, a more general

quantum mechanical evolution is abstracted from Equation 16.1. It is given by the

so-called weak solutions

→ Ψ

= e

−iht

for all Ψ

∈ L





with h being a self-adjoint, usually unbounded Hamiltonian corresponding to Equa-

tion 16.1. The domain D

of h does not comprise all of L

), yet it is dense in

(

)

. Since h is self-adjoint, the exponential e

−iht

has a unique continuous exten-

sion to L

(

)

. This unitary evolution operator e

−iht

stabilizes the domain of h as

a dense subspace of L

(

)

. Thus if and only if an initial vector Ψ

belongs to D

Equation 16.1 generalizes to

lim

ε→0

t+ε

− Ψ

− hΨ

= 0 (16.5)

for all t ∈ R. For Ψ

/∈ D

Equation 16.5 does not hold for any time.

Yet the construction of Bohmian trajectories needs much more than the evolution

→ Ψ

within L

(

)

, since the elements of L

(

)

are equivalence classes

[

]

of functions f ∈ L

(

)

. It rather needs a trajectory of functions instead of

a trajectory of equivalence classes of square-integrable functions. If there exists a

function ψ ∈ C

(

R × R

)

such that Ψ

(

t, ·

)

[

(

t, ·

)

]

holds for all t ∈ R, then ψ is

unique and the Bohmian equation of motion Equation 16.2 can be derived from the

evolution Ψ

→ Ψ

through ψ. When does there exist such ψ?

Due to Kato’s theorem (e.g., Thm X.15 of Ref. [4]) the Schrödinger Hamiltoni-

ans h, corresponding to potentials V from a much wider class than just C

∞

: R),

have the same domain as the free Hamiltonian −∆, namely the Sobolev space

(

)

. This is the space of all those Ψ ∈ L

(

)

which have all of their distribu-

tional partial derivatives up to second order being regular distributions belonging to

(

)

. Since D

is stabilized by the evolution e

−iht

, for any Ψ

∈ D

there exists,

for any t ∈ R, a function ψ

(

t, ·

)

∈ W

(

)

such that

−iht

[

(

t, ·

)

]

. (16.6)

Nondifferentiable Bohmian Trajectories 255

However, for this family of time parametrized functions ψ

(

t, ·

)

the Bohmian equation

of motion in general does not make sense since ψ

(

t, ·

)

need not be differentiable in

the classical sense.

∗

Therefore some stronger restriction of initial data than Ψ

∈ D

is needed in order

to supply the state evolution Ψ

→ e

−iht

with Bohm’s amendment. For a restricted

set of initial states

(

x, Ψ

)

and for a fairly large class of static potentials a Bohmian

evolution has indeed been constructed in Refs [5] and [6]. There it is shown that for

any Ψ

∈

n∈N

=: C

∞

there exists

• a (time independent) subset Ω ⊂ R

;

• for any t a square-integrable function ψ

(

t, ·

)

such that the restriction of ψ

(

t, ·

)

to Ω belongs to C

∞

(

Ω

)

and Equation 16.6 holds.

The set Ω is obtained by removing from R

ﬁrst the points where the potential func-

tion V is not C

∞

, second the zeros of ψ

(

0, ·

)

, and third those points x for which

the maximal solution γ

does not have all of R as its domain. Surprisingly, Ω is still

sufﬁciently large, since



Ω

(

0, x

)

x = 1.

On this reduced set Ω of initial conditions a Bohmian evolution Φ : R ×Ω → R

can

be constructed. Thus if Ψ

∈ C

∞

and if the initial position x is distributed within R

with probability density

(

0, ·

)

then the global Bohmian evolution γ

of x exists

with probability 1.

16.4 BOHMIAN EVOLUTION FOR Ψ

∈ L

\ C

∞

How about initial conditions Ψ

∈ L

(

)

∞

? Can the equation of motion Equa-

tion 16.2 still be associated with Ψ

? Hall has devised a speciﬁc counterexample

/∈ D

which leads to a wave function ψ which at certain times is nowhere differ-

entiable with respect to x and thus renders impossible the formation of the velocity

ﬁeld v. Therefore it has been suggested that the Bohmian amendment of standard

quantum mechanics is “formally incomplete” and it has been claimed that the prob-

lem is unlikely to be resolved [7].

A promising way to tackle the problem is to successively approximate the initial

condition Ψ

/∈ D

by a strongly convergent sequence of vectors





∈ C

∞

. For

each of the vectors Ψ

a Bohmian evolution Φ

exists. We do not know whether it

has actually been either disproved or proved that the sequence of evolutions does

converge to a limit Φ and that the limit depends on the chosen sequence Ψ

→ Ψ

Here we shall explore this question within the simpliﬁed setting of a spatially

one-dimensional example. We will make use of an equation for γ

which has already

∗

Only for s = 1 does Sobolev’s lemma (Thm IX.24 in Vol 2 of Ref. [4]) say that

[

(

t, ·

)

]

has a C

representative within L

(

)

. From such a C

representative ψ

(

t, ·

)

the current j follows as a continuous

vector ﬁeld and a continuous velocity ﬁeld v can be derived outside the zeros of ψ. However, v does not

need to obey the local Lipschitz condition implying the local uniqueness of its integral curves.

256 Quantum Trajectories

been pointed out in Ref. [5] and which does not rely on the differentiability of j .In

this case Equation 16.4 can be generalized in order to determine a nondifferentiable

Bohmian trajectory γ

by choosing Ω =

(

−∞, x

)

in Equation 16.4 as follows.

Consider ﬁrst the case of a C

-solution of Equation 16.1 generating a general

solution Φ : R × R → R of the Bohmian equation of motion Equation 16.2.

Since because of their uniqueness the maximal solutions do not intersect, we have

(

−∞, x

))

(

−∞, Φ

(

t, x

))

(

−∞, γ

(

))

. From this it follows by means of

Equation 16.4 that



(

)

−∞

(

t, y

)

dy =



−∞

(

0, y

)

dy. (16.7)

As a check we may take the derivative of Equation 16.7 with respect to t. This yields

(

t, γ

(

))

(

)



(

)

−∞

∂

(

t, y

)

dy = 0.

Making use of local probability conservation ∂

ρ =−∂

j we recover, by partial

integration, Equation 16.2.

Now observe that Equation 16.7 for γ

(

)

is meaningful not only when ψ is

a square integrable C

-solution of Equation 16.1 but also if ψ

(

t, ·

)

is an arbitrary

representative of Ψ

with arbitrary Ψ

∈ L

(

)

. In order to make this explicit let

: L

(

)

→ L

(

)

with x ∈ R denote the spectral family of the position operator.

For the orthogonal projection E

we have

(

)(

)



(

)

for y<x

0 otherwise.

The expectation value



Ψ, E



of E

with unit vector Ψ ∈ L

(

)

thus yields the

cumulative distribution function of the position probability given by Ψ. If we deﬁne

F : R

→

[

0, 1

]

through F

(

t, x

)



, E



, then Equation 16.7 is equivalent to

(

t, γ

(

))

= F

(

0, x

)

. (16.8)

Thus, the graph

{

(

t, γ

(

))

t ∈ R

}

of a trajectory is a subset of the level set of F which

contains the point

(

0, x

)

.IfΨ

is a sequence in L

(

)

which converges to Ψ then

lim

n→∞

(

t, x

)

= lim

n→∞

, e

iht

−iht

= lim

n→∞

−iht

= F

(

t, x

)

because e

−iht

, E

, and

are continuous mappings.

Note that for any t ∈ R the function F

(

t, ·

)

: R →

[

0, 1

]

is continuous and mono-

tonically increasing. Furthermore lim

x→−∞

(

t, x

)

= 0 and lim

x→∞

(

t, x

)

= 1.

The monotonicity is strict if ψ

(

t, ·

)

does not vanish on any interval. Thus for any

(

t, x

)

∈ R

there exists at least one γ

(

)

∈ R such that Equation Equation 16.8

holds. (For those values t for which F

(

t, ·

)

is strictly increasing, there exists exactly

one γ

(

)

∈ R such that Equation 16.8 holds.) The function F cannot be constant in

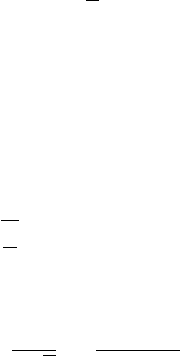
Nondifferentiable Bohmian Trajectories 257

an open neighborhood of some point

(

t, x

)

if the Hamiltonian is bounded from below.

Thus for any x ∈ R, for which there does not exist a neighborhood on which F

(

0, ·

)

is constant, we now deﬁne γ

: R → R to be the unique continuous mapping for

which

(

t, γ

(

))

= F

(

0, x

)

Note that γ

: R → R is continuous, yet need not be differentiable.

16.5 HALL’S COUNTEREXAMPLE

Let us now illustrate this construction of not necessarily differentiable Bohmian tra-

jectories by means of a solution t → Ψ

/∈ D

of the Schrödinger Equation 16.5

describing a particle conﬁned to a ﬁnite interval on which the potential V van-

ishes. This solution has been used by Hall [7] as a counterexample to Bohmian

mechanics. Similar ones have been used in order to illustrate an “irregular” decay

law t →

|

, Ψ

|

[8]. Both works have made extensive use of Berry’s earlier

results concerning this type of wave function [9].

The (reduced) classical Schrödinger equation corresponding to the quantum

dynamics is

i∂

(

t, x

)

=−∂

(

t, x

)

(16.9)

for all

(

t, x

)

∈ R×

[

0, π

]

together with the homogeneous Dirichlet boundary condition

(

t,0

)

= ψ

(

t, π

)

= 0 for all t ∈ R. The corresponding Hamiltonian’s domain D

the set of all those Ψ ∈ L

(

0, π

)

which have an absolutely continuous representative

ψ vanishing at 0 and π and whose distributional derivatives up to second order belong

to L

(

0, π

)

. As an initial condition we choose the equivalence class of the function

(

0, x

)

= 1/

√

π for all x ∈

[

0, π

]

Since within the class Ψ

[

(

0, ·

)

]

there does not exist an absolutely continuous

function vanishing at 0 and π the equivalence class Ψ

does not belong to D

.Asa

consequence for any t the vector Ψ

= e

−iht

does not belong to D

. This in turn

implies that Ψ

does not have a representative within the class of C

-functions on

[

0, π

]

with vanishing boundary values.

The Hamiltonian h is self-adjoint. An orthonormal basis formed by eigenvectors

of h is represented by the functions u

with

(

)

sin

(

)

for 0 ≤ x ≤ π and k ∈ N.

For n ∈ N the C

∞

-function ψ

: R

→ C with

(

t, x

)

√



k=0

−i

(

2k+1

)

2k + 1

sin

[

(

2k + 1

)

]

is a classical solution to the Schrödinger equation 16.9 on R

and fulﬁlls homogeneous

Dirichlet boundary conditions at x = 0 and x = π. Furthermore ψ

is periodic not

258 Quantum Trajectories

only in x but also in t with period 2π. More precisely ψ

(

t, ·

)

is an odd trigonometric

polynomial of degree 2n + 1 for any t ∈ R. In addition ψ

(

t, ·

)

is also even with

respect to reﬂection at π/2, i.e., it we have



− x



= ψ



+ x



for all x ∈ R. The functions ψ

(

·, x

)

are trigonometric polynomials of degree

(

2n + 1

)

As is well known, the sequence

(

0, ·

))

n∈N

converges pointwise on R. Its limit

is the odd, piecewise constant 2π-periodic function σ

(

0, ·

)

with

lim

n→∞

√

πψ

(

0, x

)

√

πσ

(

0, x

)



1 for 0 <x<π

0 for x ∈

{

0, π

}

(

0, ·

)

is discontinuous at x ∈ π · Z. For any t ∈ R the sequence

(

t, ·

))

n∈N

converges pointwise on R to a function ψ

(

t, ·

)

. For rational t/π this function is

piecewise constant [9]. However for irrational t/π the real and imaginary parts of

(

t, ·

)

restricted to any open real interval have a graph with noninteger dimension [9].

Thus for irrational t/π the function ψ

(

t, ·

)

is nondifferentiable on any real interval.

As an illustration we give in Figure 16.1 the graph of

x →

√

πψ

500



√

, πx



1.4

1.2

0.8

0.6

0.4

0.2

–0.2

–0.4

0 0.05 0.1 0.15 0.2 0.25 0.3

0.35 0.4 0.45 0.5

FIGURE 16.1 Real part of ψ

500

at a ﬁxed time.

Nondifferentiable Bohmian Trajectories 259

for 0 <x<1/2 together with the partial sum over k ∈

{

501, ...,750

}

visible as the

small noisy signal along the abscissa

x →

√



750



π/

√

12, πx



− ψ

500



π/

√

12, πx



Similarly, for given x ∈

(

0, π

)

the mapping t → ψ

(

t, x

)

does not belong to the

set of piecewise C

-functions on

[

0, 2π

]

. This can be seen as follows. First note that

for given x the 2π-periodic function ψ

(

·, x

)

has the Fourier expansion

(

t, x

)

∞



k=1

−int

where







√

2k + 1

sin

[

(

2k + 1

)

]

for n =

(

2k + 1

)

with k ∈ N

0 otherwise.

Assume now that ψ

(

·, x

)

is piecewise C

. Then, according to a well known property

of Fourier coefﬁcients, there exists a positive real constant C such that n

<Cfor

all n ∈ N. This implies that

(

2k + 1

)

sin

[

(

2k + 1

)

]



for all k ∈ N (16.10)

with the positive constant C



= π

√

πC/4. However, for x /∈ π · Z there exists

some real constant ε > 0 such that the set

{

k ∈ N :

sin

[

(

2k + 1

)

]

> ε

}

contains

inﬁnitely many elements. Thus for x /∈ π ·Z the estimate Equation 16.10 cannot hold

and therefore the function t → ψ

(

t, x

)

cannot be piecewise C

[

0, π

]

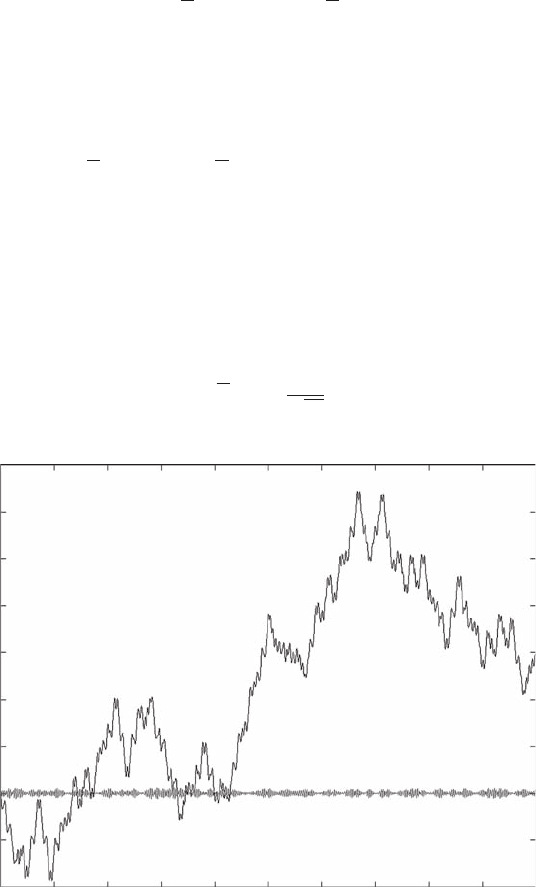
In Figure 16.2 we plot the time dependence

t →

√

πψ

(

πt, π/2

)



k=0

(

−1

)

2k + 1

cos



(

2k + 1

)

πt



for 0 <t<1/2 together with the partial sum

t →

√

(

πt, π/2

)

− ψ

(

πt, π/2

))

(noisy signal along the abscissa).

The restriction of the limit σ

(

0, ·

)

[

0, π

]

represents the same L

element as

(

0, ·

)

does. Thus lim

n→∞



(

0, ·

)



− Ψ

= 0, when

denotes the restriction

of ψ

to R×

[

0, π

]

. Correspondingly ρ

(

0, ·

)

(

0, ·

)

converges toward the den-

sity of the equipartition on

[

0, π

]

. Additionally, due to the continuity of the evolution

operator e

−iht

, the sequence of equivalence classes



(

t, ·

)



∈ C

∞

approximates

the L

vector Ψ

= e

−iht

, i.e., for all t we have

lim

n→∞



(

t, ·

)



− Ψ

= 0.

Since also E

: L

(

)

→ L

(

)

is continuous, the time dependent cumulative

position distribution function F : R ×

[

0, π

]

→

[

0, 1

]

with F

(

t, x

)



, E



obeys

260 Quantum Trajectories

2.5

1.5

0.5

–0.5

–1

0 0.05 0.1 0.15 0.2 0.25 0.3

0.35 0.4 0.45 0.5

FIGURE 16.2 Real part of ψ

at x = π/2.

0.25

0.2

0.15

0.1

0.05

0.25

0.2

0.15

0.1

0.05

0.25

0.2

0.15

0.1

0.05

0 0.1 0.2 0.3 0.4 0.5

n = 5

0 0.1 0.2 0.3 0.4 0.5

n = 10

0 0.1 0.2 0.3 0.4 0.5

n = 20 Space

Time

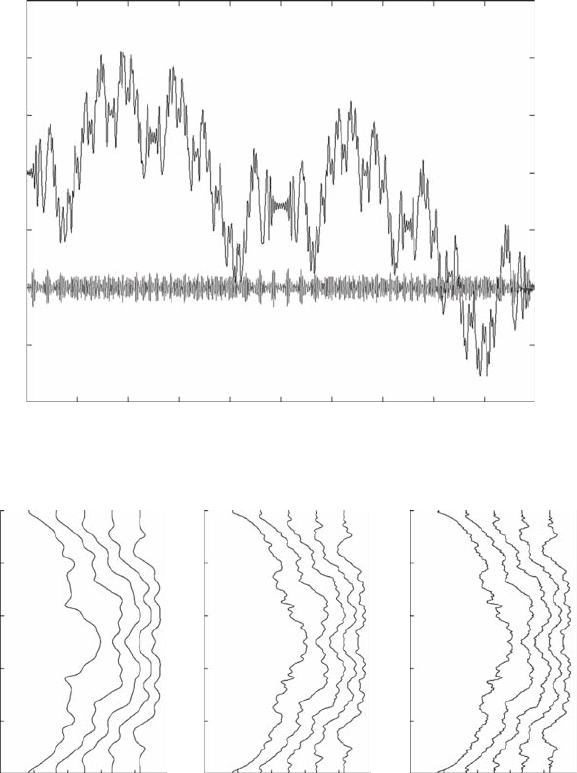
FIGURE 16.3 Level lines of F

for n = 5, 10, 20.

(

t, x

)

= lim

n→∞

1

(

t, ·

)



, E



(

t, ·

)

2

= lim

n→∞



(

t, y

)

dy.

The level lines of the functions F

: R ×

[

0, π

]

→

[

0, 1

]

with F

(

t, x

)



(

t, y

)

dy thus converge to the continuous level lines of F .

Figure 16.3 shows some level lines of F

for n = 5, 10, 20 starting off at equal

positions at t = 0. The level lines inherit the period π/4 of F

(

·, x

)

, which has this

period since the frequencies appearing in the even function

(

·, x

)

are 0, 8, 16, . . .

Nondifferentiable Bohmian Trajectories 261

0.25

0.2

0.15

0.1

0.05

0 0.1 0.2 0.3 0.4 0.5 0.6

n = 1000

Time

Space

0.7 0.8 0.9 1

FIGURE 16.4 Level lines of F

1000

Figure 16.4 shows the case n = 1000. Increasing n from 20 to 1000 hardly alters

the level lines.

BIBLIOGRAPHY

1. B. Aulbach, Gewöhnliche Differenzialgleichungen, Elsevier, Amsterdam, 2004.

2. D. Dürr and S. Teufel, Bohmian Mechanics, Springer, Berlin, 2009.

3. K. Berndl, Global existence and uniqueness of Bohmian trajectories, arXiv:quant-

ph/9509009, 1995. Published in: Bohmian Mechanics and Quantum Theory: An Appraisal,

Eds. J.T Cushing, et al., Kluwer, Dordrecht, 1996.

4. M. Reed and B. Simon, Methods of Modern Mathematical Physics II,Academic press, New

York, 1975.

5. K. Berndl, et al., On the global existence of Bohmian mechanics, Comm. Math. Phys. 173

(1995) 647–73.

6. S. Teufel and R. Tumulka, Simple proof of global existence of Bohmian trajectories, Comm.

Math. Phys. 258 (2004) 349–65.

7. M.J.W. Hall, Incompleteness of trajectory-based interpretation of quantum mechanics,

J. Phys. A37 (2004) 9549–56.

8. P. Exner and M. Fraas, The decay law can have an irregular character, J. Phys. A40 (2007)

1333–40.

9. M.V. Berry, Quantum fractals in boxes, J. Phys. A29 (1996) 6617–29.

Nonadiabatic Dynamics

with Quantum Trajectories

Gérard Parlant

CONTENTS

17.1 Introduction.................................................................................................263

17.2 Theory.........................................................................................................265

17.2.1 Quantum Trajectory Equations for Nonadiabatic Dynamics........265

17.2.2 Algorithm and Numerical Details .................................................267

17.3 Discussion...................................................................................................269

17.3.1 Application of the Exact Multistate Quantum Trajectory

Method..........................................................................................269

17.3.2 Mixed Representations..................................................................271

17.3.2.1 Mixed Coordinate-Space/Polar Representation ............271

17.3.2.2 Decoupled Representation.............................................272

17.3.3 Bipolar Wave Packets ...................................................................276

17.4 Summary and Conclusion...........................................................................279

Appendix: Diabatic and Adiabatic Electronic Representations .............................280

Bibliography ..........................................................................................................280

17.1 INTRODUCTION

Chemical reaction dynamics [1] can often be described in the framework of the

Born–Oppenheimer approximation as the evolution from reactants to products on a

single adiabatic potential energy surface (PES). However, this approximation may

become invalid if the relevant PES happens to be energetically close to another one,

for example near a conical intersection [2], in which case nonadiabatic transitions

between these electronic states become likely [3]. Reaction dynamics on coupled

PESs is governed by two quantum effects: (i) population transfer from one electronic

state to another, and (ii) phase coherence between the nuclear wave packets evolving

on each state, with these two effects reciprocally inﬂuencing each other. Therefore,

nonadiabatic dynamics is a highly nonclassical process, which must be treated quan-

tum mechanically. Various methods have been proposed to describe the concerted

motion of nuclei on coupled electronic states and we refer the reader to Burghardt

and Cederbaum [4] for a recent bibliography. In this chapter, we introduce and discuss

a formally exact description of nonadiabatic dynamics using quantum trajectories.

Based on the de Broglie–Bohm formulation of quantum mechanics [5–10], the—

formally exact—Quantum Trajectory Method (QTM), originally developed by Wyatt

263