Charles M. Kozierok The TCP-IP Guide

Подождите немного. Документ загружается.

Binary, Octal and Hexadecimal Arithmetic

Many of us use arithmetic every day as part of our regular lives without really noticing it, to

give us the information we need to make decisions. In a similar way, computers perform

arithmetic operations all the time as part of their normal operation. The main differences

between how computers do it and how we do it are two-fold: computers use binary

numbers, and computers are much faster.

As I said in my introduction to binary, octal and hexadecimal numbers, those forms are

different representations of numbers, and are not really much different than decimal

numbers. They just have a different number of values per digit. In a similar vein, arithmetic

with binary, octal or hexadecimal numbers is not that much different from the equivalent

operations with decimal numbers. You just have to keep in mind that you are working with

powers of 2, 8 or 16, instead of 10, which isn’t always easy to do.

As was the case with conversions, calculators are usually the way to go if you need to do

math with binary, octal or hexadecimal numbers. If your calculator only does math with

decimal numbers, one trick is to convert the numbers to decimal, then perform the

operation, and convert back the result. However, you can fairly easily do the same addition,

subtraction, multiplication and division on binary, octal or hex numbers that you do with

decimal numbers, by using the Windows Calculator program or equivalent.

Multiplication and division of binary numbers is a common operation within computers, but

isn't a calculation that often needs to be done by people who are working with them.

Addition and subtraction are much more common (especially addition), and have the added

bonus of being much easier to explain. You probably won't need to do this type of arithmetic

that often, but it's good to understand it, at least a little. I am going to provide just a couple

of examples to give you the general idea.

Binary Arithmetic

Let's start with binary. Adding binary numbers is the same as adding decimal ones, but you

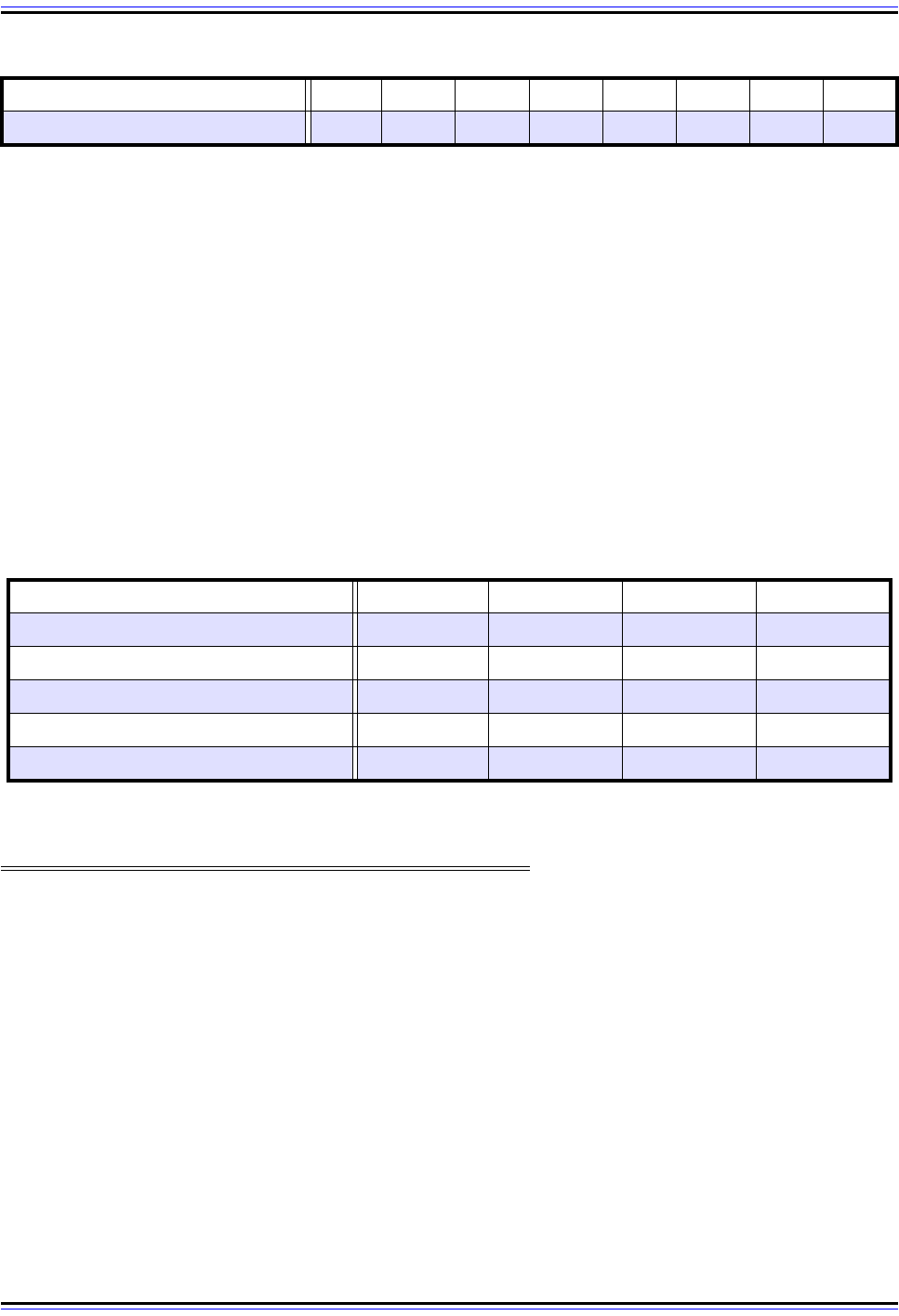
end up doing a lot of carrying of ones since there are so few values allowed per digit. Table

8 shows an example, with one digit in each column; read it from right to left and top to

bottom, just as you would usually do manual addition. So we start by adding the "1" in the

"ones" place from the first number with the "1" in that place from the second number,

yielding a raw digit sum of 2. This means the result for the "ones" digit is "1" and we carry a

1 to the "twos" place. We continue with this process until we have added all the digits.

Table 8: Binary Addition

Carry 11 11—

First Binary Number 1 0 1 1 0 0 1 1

Second Binary Number 00111001

Raw Digit Sum 1 1 3 2 1 1 2 2

Octal and Hexadecimal Arithmetic

Octal and hexadecimal are pretty much the same, except that you carry if the sum in a

particular digit exceeds either 8 or 16, respectively. Hexadecimal is more common, and

more interesting, so let's take an example of adding two hex numbers together. While

performing the operation, you will need to do conversions of single-digit hex numbers to

decimal and back again, but this isn't too difficult.

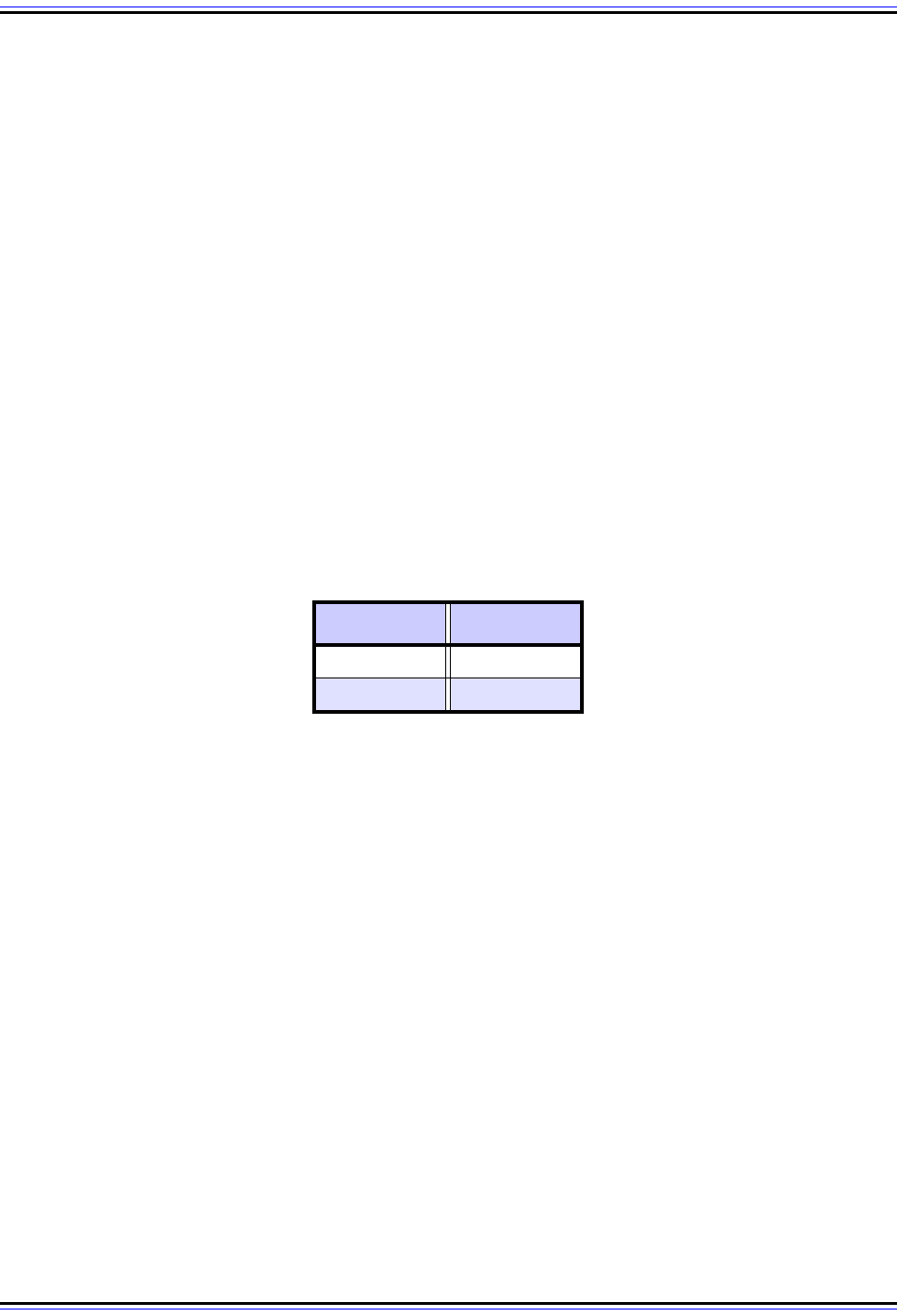
This example is shown in Table 9, which again should be read from right to left. We start by

adding "8" (decimal 8) to "A" (decimal 10) in the "ones" place. This yields a raw sum of 18,

from which we carry 16 as a "1" to the "16s" place and leave a result of 2. We add this 1 to

the "D" (value 13) and "E" (14 value) of the "16s" place. This is a total of 28, leaving 12 ("C"

in hexadecimal) and we carry a 1 to the "256s" place. This continues until we are left with a

sum of 6DC2h.

Boolean Logic and Logical Functions

Every bit in a computer system can hold a value of either “one” or “zero”, which represent

the basic “on” or “off” states inherent in a binary digital system. In the preceding topics in

this section, I demonstrated how groups of these bits can be collected into sets to represent

larger binary numbers, and then how those can be used for performing various mathe-

matical operations.

However, as I mentioned when I introduced the concept of binary information, we can also

interpret the “on” and “off' values of a binary digit as “true” or “false” respectively. These can

represent various logical conditions within a computer or other system. Furthermore, there

are various logical operations that can be used to manipulate and combine these “true” or

“false” values to represent more complex logical states. One of the pioneers of using binary

values in logical thought was British mathematician George Boole (1815-1864), and in

recognition of his contribution to this field, this system of binary values and conditions is

commonly called boolean logic.

Result 11101100

Carry to Next Higher Digit 1 1 1 1

Table 9: Hexadecimal Addition

Carry 11

First Hex Number 2 C D 8

Second Hex Number 40EA

Raw Digit Sum 2+4 = 6 1+12+0 = 13 1+13+14 = 28 8+10 = 18

Result 6DC2

Carry to Next Higher Digit 1 1

Table 8: Binary Addition

Boolean Logical Functions

Boolean logic defines a number of boolean logical functions, which are also sometimes

called operators. Each of these uses a logical algorithm to compute an output value based

on the value of one or more inputs. The algorithm determines when the output is a “true”

value, based on what combination of “true” and “false” values the inputs take. For this

reason, the table that shows the inputs and outputs for a logical function is called a truth

table. Each of the logical functions is analogous to a “real world” logical operation that we

use to define various logical situations, as we will see.

It is much easier to see how boolean logic works by looking at examples, rather than

reading these types of formal descriptions. So, let's just jump right in and see it in action, by

looking at the different functions and how they work.

The NOT Function

Let's start with the simplest, the NOT function. As you might expect, this is a just a negation;

the output is the opposite of the input. The NOT function takes only one input, so it is called

a unary function or operator. The truth table for NOT is shown in Table 10. As you can see,

the output is true when the input is false, and vice-versa.

The NOT function logically represents the opposite of a condition. For example, suppose

we have a bit called “B1” whose logical meaning is that when the bit is “true”, a particular

pixel on a screen is lit up. Then the boolean expression “NOT B1” would be the opposite: it

would be false when the pixel is lit up, and thus true only when the pixel is not lit up. Pretty

straight-forward.

Now, before proceeding further, I am going to play a little trick on you. ☺ As I said above,

boolean logic is based on “true” and “false” values. However, I also said that “true” and

“false” are represented in computers by “one” or “zero” values. For this reason, boolean

logic is often expressed in terms of ones and zeroes, instead of “true” and “false”. The

circuits inside computer processors and other devices manipulate one and zero bits directly

using these functions. In some (but not all) cases they interpret “one” and “zero” as “true”

and “false”, but in either case the two representations are functionally equivalent.

Table 10: NOT Operator Truth Table

Input Output

False True

True False

Table 11 shows the same truth table as Table 10, but using bit values: each "True" is repre-

sented as a 1 and each "False" as a 0.

The AND and OR Functions

There are two other primary boolean functions that are widely used: the AND function and

the OR function. The output of an AND function is true only if its first input and its second

input and its third input (etc.) are all true. The output of an OR function is true if the first

input is true or the second input is true or the third input is true (again, etc.)

Both AND and OR can have any number of inputs, with a minimum of two. Table 12 shows

the truth table for the AND function, with two inputs. You can see that the output is a 1 only

when both inputs are 1, and is 0 otherwise.

Like the NOT function, the AND function represents a logical operation similar to how we

use the word in our every day lives. For example, at lunch time, I might suggest to a

colleague "let's go out for lunch and stop at the post office".

The truth table for the OR function (again with two inputs) is shown in Table 13. Here, the

output is 1 whenever a 1 appears in at least one input, not necessarily both as in the

previous table.

Table 11: NOT Operator Truth Table (Using Bit Values)

Input Output

0 1

1 0

Table 12: AND Operator Truth Table

Input #1 Input #2 Output

000

0 1 0

100

1 1 1

Table 13: OR Operator Truth Table

Input #1 Input #2 Output

000

0 1 1

101

1 1 1

Interestingly, unlike the AND function, the boolean OR function in fact does not have the

same meaning as the way that we routinely use the word “or” in English. When we say “or”,

we usually mean one “or” the other, but not both: “you can have apple pie or chocolate cake

for dessert”. In the boolean OR however, the output is true as long as any of the inputs is

true, even if more than one is.

Exclusive-OR (XOR or EOR)

A modification of OR called Exclusive-OR (abbreviated either XOR or EOR) represents the

way we normally use “or” in the real world. Its output is only true if one input is true or the

other, but not both. The truth table for XOR is as shown in Table 14. Notice the difference

between this table and Table 13: the output is 0 in the case where both inputs is 1.

Combining Boolean Functions to Create Boolean Expressions

The functions described above can also be combined in arbitrary ways to produce more

complex logical conditions. Boolean logic expressions are used in many different contexts

in the computing field. A common place that most people use them is in a World Wide Web

search engine. For example, if you enter “cheese AND (cheddar OR swiss) NOT wisconsin”

into a search engine, the program will return pages that contain the word “cheese” that also

contain the word “cheddar” or “swiss” (or both), but that do not contain the word

“wisconsin”.

(Sorry, Wisconsinite cheese lovers—but I live in Vermont! ☺)

Boolean functions are the building blocks of much of the circuitry within computer hardware.

The functions are implemented as tiny gates that are designed to allow electrical energy to

flow to the output only based on certain combinations of inputs as described by the truth

tables for functions like NOT, AND, OR and others. In networking, boolean logic is important

for describing certain conditions and functions in the operation of networks. Boolean

functions are also very important because they are used to set, clear and mask strings of

binary digits, which we will explore in the next topic.

Table 14: Exclusive OR (XOR) Operator Truth Table

Input #1 Input #2 Output

000

0 1 1

101

1 1 0

Key Concept: Boolean logic is a system that uses boolean functions to produce

outputs based on varying conditions in their input data. The most common boolean

functions are NOT, which produces as output the opposite of its input; AND, which is

true (1) only if all of its inputs are true (1); OR, which is true if any of its inputs is true; and

XOR, which is true only if exactly one of its inputs is true (or put another way, if the inputs

are different). These functions can be used in boolean logic expressions that represent

conditional states for making decisions, and can also be used for bit manipulation.

Bit Masking (Setting, Clearing and Inverting) Using Boolean

Logical Functions

The boolean functions NOT, AND, OR and XOR describe different ways that logical expres-

sions can be used to manipulate “true” and “false” values to represent both simple and

complex decisions or conditions. However, these functions can also be used in a more

mundane manner, to allow the direct manipulation of binary data. This use of boolean logic

is very important in a number of different applications in networking.

As I mentioned in the topic introducing binary numbers, giving a bit a value of one is called

setting the bit, while giving it a value of zero is either resetting or clearing it. In some situa-

tions bits are handled “individually”, and are set or cleared simply by assigning a one or

zero value to each bit. However, it is common to have large groups of bits that are used

collectively to represent a great deal of information, where many bits need to be set or

cleared at once. In this situation, the boolean functions “come to the rescue”.

Setting Groups of Bits Using the OR Function

Setting bits en masse can be done by exploiting the properties of the OR function. Recall

that the OR function's output is true (one) if any of its inputs is true (one). Thus, if you “OR”

a bit with a value known to be one, the result is always going to be a one, no matter what

the other value is. In contrast, if you “OR” with a zero, the original value, one or zero, is not

changed.

By using a string with zeroes and ones in particular spots, you can set certain bits to 1 while

leaving others unchanged. This procedure is comparable to how a painter masks areas that

he does not want to be painted, using plastic or perhaps masking tape. Thus, the process is

called masking. The string of digits used in the operation is called the bit mask, or more

simply, just the mask.

An example will illustrate. Suppose we have the 12-bit binary input number 101001011010,

and we want to set the middle six bits to be all ones. To do this, we simply OR the number

with the 12-bit mask 000111111000. Table 15 shows how this works, with the changed bits

in the result highlighted—we simply OR each bit in the input with its corresponding bit in the

mask:

Clearing Groups of Bits Using the AND Function

To clear a certain pattern of bits, you do a similar masking operation, but using the AND

function instead. If you AND a bit with zero, it will clear it to zero regardless of what the bit

was before, while ANDing with one will leave the bit unchanged. So, to take the same

example above and clear the middle six bits, we AND with the reverse bit mask,

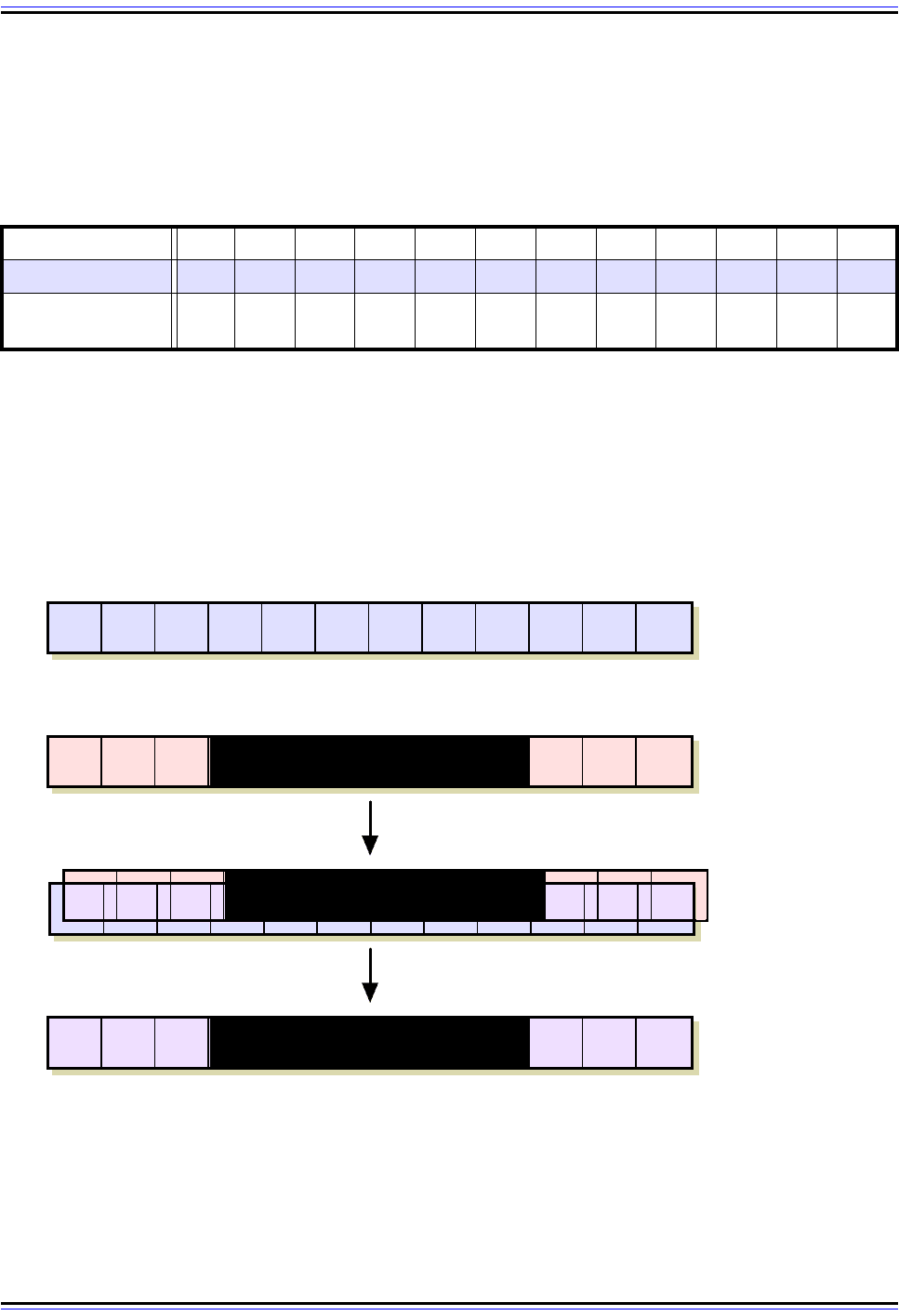
111000000111. This is shown in Table 16 and illustrated in Figure 10.

Table 15: Setting Bits Using an OR Bit Mask

Input 101001011010

Mask 0 0 0 1 1 1 1 1 1 0 0 0

Result of OR

Operation

101111111010

Figure 10: Clearing Bits Using an AND Bit Mask

This diagram shows how a bit mask can be used to clear certain bits in a binary number while preserving

others. The mask shown here can be likened to a painter’s mask; each 1 represents a “transparent” area that

keeps the corresponding input bit value, while each 0 is a bit where the original value is to be cleared. After

performing an AND on each bit pair, the first three and last three bits are preserved while the middle six, since

they were each ANDed with 0, are forced to 0 in the output.

1 0 1 0 0 1 0 1 1 0 1 0 Input

Bit Mask1 1 1 0 0 0 0 0 0 1 1 1

1 0 1 0 0 0 0 0 0 0 1 0

Masking

Output

1 0 1 0 0 1 0 1 1 0 1 0

We can also look at this “clearing” function a different way. We are clearing the bits where

the mask is a zero, and in so doing “selecting” the bits where the mask is a one. Thus,

ANDing with a bit mask means that you “keep” the bits where the mask is a one and

“remove” the bits where it is a zero.

Inverting Groups of Bits Using the XOR Function

There are also situations in which we want to invert some bits; that is, change a one value

to a zero, or a zero value to a one. To do this, we use the XOR function. While this is not as

intuitive as the way masking works with OR and AND, if you refer to the XOR truth table

(Table 14) you will see that if you XOR with a one, the input value is flipped, while XORing

with a zero causes the input to be unchanged. To see how this works, let's take the same

input example and invert the middle six bits, as shown in Table 17.

In the world of networking, bit masking is most commonly used for the manipulation of

addresses. In particular, masking is perhaps best known for its use in differentiating

between the host and subnetwork (subnet) portions of Internet Protocol (IP) addresses, a

process called subnet masking and described in the section on IP subnet addressing.

Note: Masks are often expressed in either hexadecimal or decimal notation for

simplicity of expression, as shown in the IP subnetting summary tables. However,

the masks are always applied in binary, as described above. You should convert

the mask to binary if you want to see exactly how the masking operation is going to work.

Table 16: Clearing Bits Using an AND Bit Mask

Input 101001011010

Mask 1 1 1 0 0 0 0 0 0 1 1 1

Result of AND

Operation

101000000010

Table 17: Inverting Bits Using an XOR Bit Mask

Input 101001011010

Mask 0 0 0 1 1 1 1 1 1 0 0 0

Result of XOR

Operation

101110100010

Key Concept: The properties of the OR and AND boolean functions make them

useful when certain bits of a data item need to be set (changed to 1) or cleared

(changed to 0), a process called bit masking. To set bits to one, a mask is created

and used in a bit-by-bit OR with the input; where the mask has a value of 1, the bit is forced

to a 1, while each 0 bit leaves the corresponding original bit unchanged. Similarly, a mask

used with AND clears certain bits; each 1 bit in the mask leaves the original bit alone, while

each 0 forces the output to 0. Finally, XOR can be used to invert selected bits using a mask.

The Open System Interconnection (OSI) Reference

Model

Models are useful because they help us understand difficult concepts and complicated

systems. When it comes to networking, there are several models that are used to explain

the roles played by various technologies, and how they interact. Of these, the most popular

and commonly used is the Open Systems Interconnection (OSI) Reference Model.

The idea behind the OSI Reference Model is to provide a framework for both designing

networking systems and for explaining how they work. As you read about networking, you

will frequently find references to the various levels, or layers, of the OSI Reference Model.

The existence of the model makes it easier for networks to be analyzed, designed, built and

rearranged, by allowing them to be considered as modular pieces that interact in

predictable ways, rather than enormous, complex monoliths.

In fact, it's pretty much impossible to read a lot about networking without encountering

discussions that presume at least some knowledge of how the OSI Reference Model works.

This is why I strongly advise that if you are new to the OSI Reference Model, you read this

chapter carefully. While it is all arguably “background material”, reading it will help form an

important foundation in your understanding of networks, and will make the rest of the Guide

make more sense at the same time.

If you are quite familiar with the OSI Reference Model, you may wish to skip this chapter of

the Guide, or just skim through it. You can always return later to brush up on particular

issues, as needed. There are also many links that come back to the descriptions of the

individual layers from various parts of the Guide.

In the pages that follow, I describe the OSI Reference Model in detail. I begin with a history

of the model, and a discussion of some general concepts related to the OSI model and

networking models overall. I provide a useful analogy to help you understand how the

reference model works to explain the interaction of networks on multiple levels. I then

describe each of the seven layers of the OSI Reference Model, and conclude with a

summary of the layers and their respective functions.

Note: This section describing the OSI Reference Model is geared to a discussion

of networks and internetworks in general, and not specifically to the TCP/IP

protocol suite. Therefore, not all of the material in this section is directly relevant to

learning about TCP/IP, though much of it is. You may also wish to refer to the topic covering

the reference model that describes TCP/IP, which also discusses how the TCP/IP and OSI

models compare.