Charles M. Kozierok The TCP-IP Guide
Подождите немного. Документ загружается.

The TCP/IP Guide - Version 3.0 (Contents) ` 121 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
Binary Information Representation and Groups
The fundamental building block of computer information is the bit (a contraction of binary
digit). Every bit can be either 0 or 1. Making the value of a bit 1 is commonly called setting
the bit; changing it to 0 is resetting or clearing it.
Of course, bits represent only a very small amount of information: a single fact or value. We
must make collections of these bits so we can use them to store large amounts of infor-
mation and more complex data types. The most common grouping is to take eight bits and
reference them as a single unit. A collection of eight bits is technically called an octet, but is
more commonly called a byte. (More on that in a moment.)
“Byte” is a jocular play on the term “bit”. Over time, other sizes of “bit collections” have also
been defined. Some geek comedian decided that if eight bits made a “byte”, then four bits
must be a “nybble” (or “nibble”). Hilarious. ☺ Larger collections have also been defined and
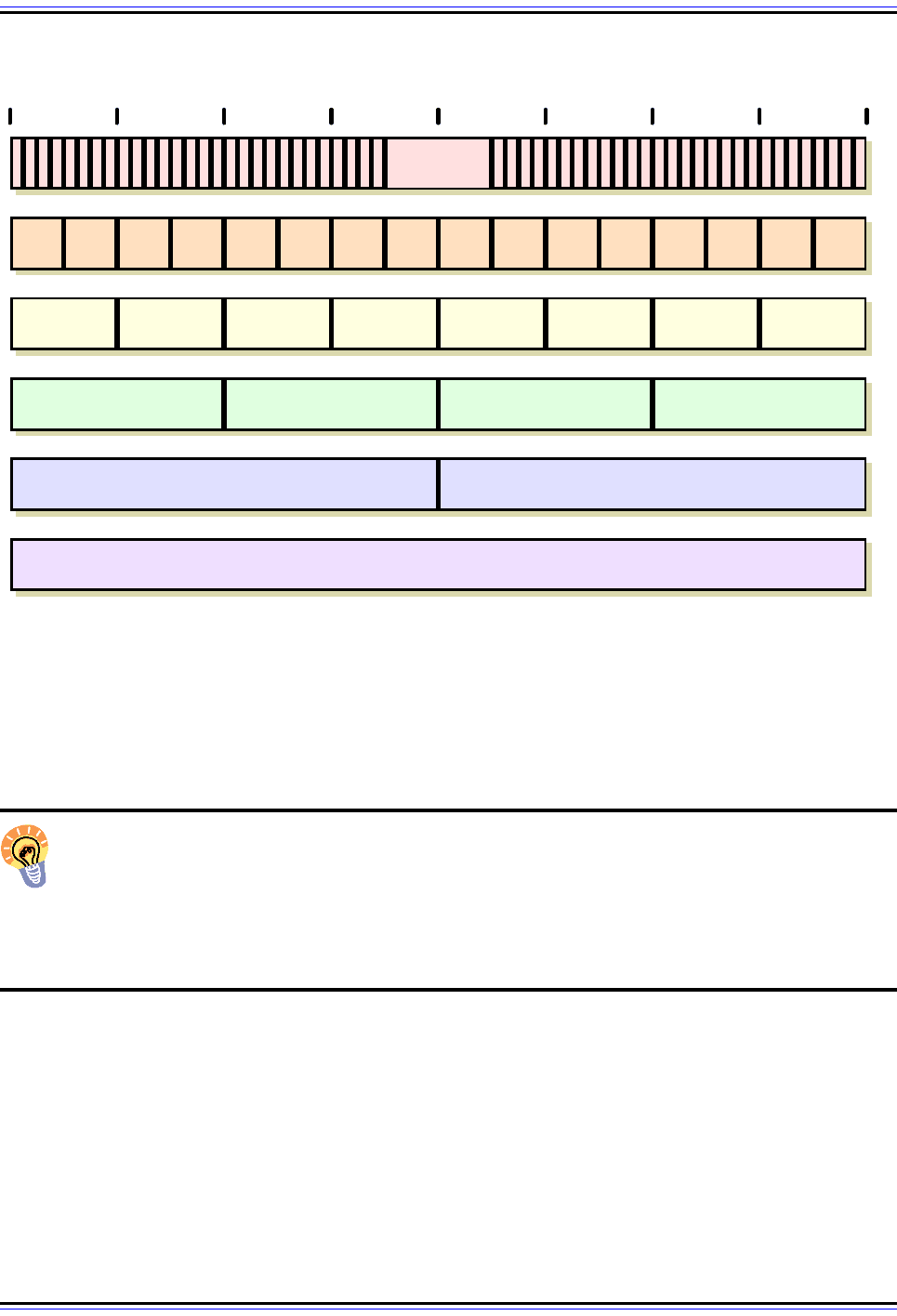
given various names. Table 2 summarizes the most common representations of groups of
bits, and the terms used for them; their relative sizes are also shown graphically in Figure 8.
A few of these terms are worth special mention. Bit and byte we have already discussed, of
course. A bit is also sometimes called a flag; this term is most often heard when a bit is
used by itself to represent a particular information state. For example, a computer might use
a “changed flag” to represent whether a particular file has been modified; this is an analogy
to a flag either being raised or lowered to indicate a condition. These “flags” are often seen
in networking message formats.
The term character is also used to express a set of eight bits. This use comes from the fact
that computers often store alphanumeric characters, such as letters and numbers, one to a
byte. The 16-bit word is fairly often used, but not nearly as much as “byte”. The larger
collections of bits, such as double word and so on, are not often encountered in every-day
parlance; they are used to represent chunks of data in technical fields such as hardware
design or programming.
You may also have noticed the number of bits used for each of these terms is a power of
two. This is of course not a coincidence. As we will see in the subsequent topics in this
section, this occurs because when bits come in sets that are a power of two in size, they are
Table 2: Binary Information Group Representations and Terms
Number of
Bits
Common Representation Terms
1 Bit / Digit / Flag
4 Nybble / Nibble
8 Byte / Octet / Character
16 Double Byte / Word
32 Double Word / Long Word
64 Very Long Word
The TCP/IP Guide - Version 3.0 (Contents) ` 122 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
easier to represent and manipulate in a convenient manner. The number of bits in the term
can itself be easily expressed using binary numbers. This will make more sense after you
read the topic that follows on decimal binary, octal and hexadecimal numbers.
Key Concept: Computers store all information in binary digital form, which means all
data—be it text, photographs, audio or whatever else—is comprised only of collec-
tions of ones and zeroes. The fundamental building block of digital information is the
binary digit or bit, which represents a single zero or one state. To represent larger amounts
of information, bits can be collected into groups of four, eight, sixteen, 32 or 64, called
nybbles, bytes, words, long words and very long words respectively.
Byte versus Octet
There has been some disagreement, and even controversy, surrounding the use of the
words byte and octet. The former term has traditionally been the most popular in common
parlance for a set of eight bits, especially in North America. However, it is technically not
the correct term.
Figure 8: Binary Information Representations and Terms
This diagram shows the relative sizes of the most commonly-sized “collections” of binary information.
Very Long Word
Long Word Long Word
Word Word Word Word
Byte Byte Byte Byte Byte Byte Byte Byte
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Nyb
ble
Bits
8 162432404856640

The TCP/IP Guide - Version 3.0 (Contents) ` 123 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
A byte is, formally, the smallest unit of data that can be read from or written to at one time in
a computer system. In almost all cases today, that is indeed eight bits, but there are have
been some systems where a byte was not eight bits. Some older 36-bit computers used 9-
bit bytes, and there were also systems that had byte sizes of 6 or 7 bits, or even variable-
sized bytes. For this reason, many people, especially techie professionals, prefer the term
octet, which clearly and unambiguously implies “eight”. This term is much more common
outside North America.
This matter of octets and bytes is another of the little “tempests in tea pots” that computer
people seem to love so much. The bottom line in modern computer systems, however, is
that an octet is a byte and a byte in an octet, and the terms can be used interchangeably
without too much danger. You will more often see octets used in technical standards. In this
Guide, I use the term bytes for a simple reason: it is the term that most people are familiar
with, including myself (though bear in mind that I live in North America; if I were European I
might have rather different views on this!)
Key Concept: Formally, an octet is the correct term for exactly eight bits, while a
byte is the smallest number of bits that can be accessed in a computer system,
which may or may not equal eight. In practice, modern computers use 8-bit bytes,
and the terms are used interchangeably (with byte being more common in North America,
and octet often being preferred in Europe).
Decimal, Binary, Octal and Hexadecimal Numbers
The numbers we are used to using in every-day life are called decimal numbers, where the
word “decimal” refers to the number ten. The reason for this is rather obvious: every digit
can take on one of ten values: 0 to 9. Arithmetic performed on decimal numbers is also
called base 10 mathematics, because of this orientation around the number 10. (Why is the
number 10 the foundation of our normal mathematical system? Hold both hands up and
count…)
Computer systems, however, don’t have fingers or toes; they deal only with binary
numbers. Each bit can represent not a value from 0 to 9, but from, well, 0 to 1. A single “0 or
1” value is sufficient for encoding a single fact, such as whether your car currently is using
summer tires or snow tires. It's not nearly enough to hold more complex information, such
as your bank account balance, or a text document, or a picture of the Yellowstone canyon.
Binary Numbers and their Decimal Equivalents
For this reason, larger collections of bits have been defined by computer scientists, such as
bytes (octets), words, and so forth. When individual bits are collected into sets in this way,
they can be used together to represent larger integers, which are called binary numbers.
Since there are only two possible values for each digit, binary numbers are also called base
2 numbers.

The TCP/IP Guide - Version 3.0 (Contents) ` 124 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
A lot of people are intimidated by binary numbers, because at first they seem quite
confusing. The key to understanding them is realizing that they are exactly the same as
decimal numbers, except that instead of each digit having a value in the range of 0 to 9,
each has a value in the range of 0 to 1. For example, when you count in decimal, you go up
to 9 in the one’s place, and then you need a second place for “tens”. If you go above 99,
you need a third place for “hundreds”. Each additional place added on the left is a higher
power of ten. Binary is the same, except the limit for each place is 1 instead of 9. In binary,
you go up to 1 in the one’s place, and then need a second place for “twos”. If you go above
3, you need a third place for “fours”. Each added place is a subsequent higher power of two,
rather than ten.
Thus, where counting in decimal goes 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 and so on,
counting in binary goes 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100,
1101. The concept is identical—you just need a lot more digits for binary numbers because
there are so many fewer values allowed for each digit. For example, the number “13” in
decimal is the same as “1101” in binary. How? Well, in decimal, we have a 3 in the one’s
place, plus a “1” in the “tens” place, which has a value of 10. This is 3+10=13. In binary, we
have a “1” in the “ones” place, plus a “1” in the “fours” place, plus a “1” in the “eights” place,
which is 1+4+8 or 13.
To take a more complex example, 211 in decimal is 11010011 in binary. Table 3 shows how
the two are equivalent, by adding the values for each binary digit place where there is a 1.
Read it from left to right, going top to bottom. Starting in the left-most column, we see that
the example number has a 1 in the "128s" place. So we start with a sum of 128. In the next
column there is a 1 in the "64s" place, so we add 64 for a running sum of 192. But in the
"32s" place the binary digit value is 0, so we don't add 32 to the sum. We continue down to
the "ones" place to get the decimal equivalent of the binary number.
As you can see from this, a binary number with N digits can hold up to 2
N
values. So, a
byte, with eight bits, can hold 2
8
or 256 different values, which are numbered from 0 to 255.
A 16-bit word can hold 2
16
or 65,536 values.
Making Binary Numbers Easier to Use By Grouping Bits
One problem with binary numbers is that while computers love them, they are unintuitive for
humans, who are used to decimal numbers. One reason for this is that they quickly get very,
very long and cumbersome to deal with. For example, 1,000,000 in decimal is
Table 3: Binary and Decimal Number Equivalents
Binary Number 11010011
Power of Two
2
7
2
6
2
5
2
4
2
3
2
2
2
1
2
0
Value of Digit Place 1286432168421
Value For This
Number
128 64 0 16 0 0 2 1
Running Sum (from
left to right)
128
128+64
= 192
192
192+16
= 208
208 208
208+2 =
210
210+1 =
211
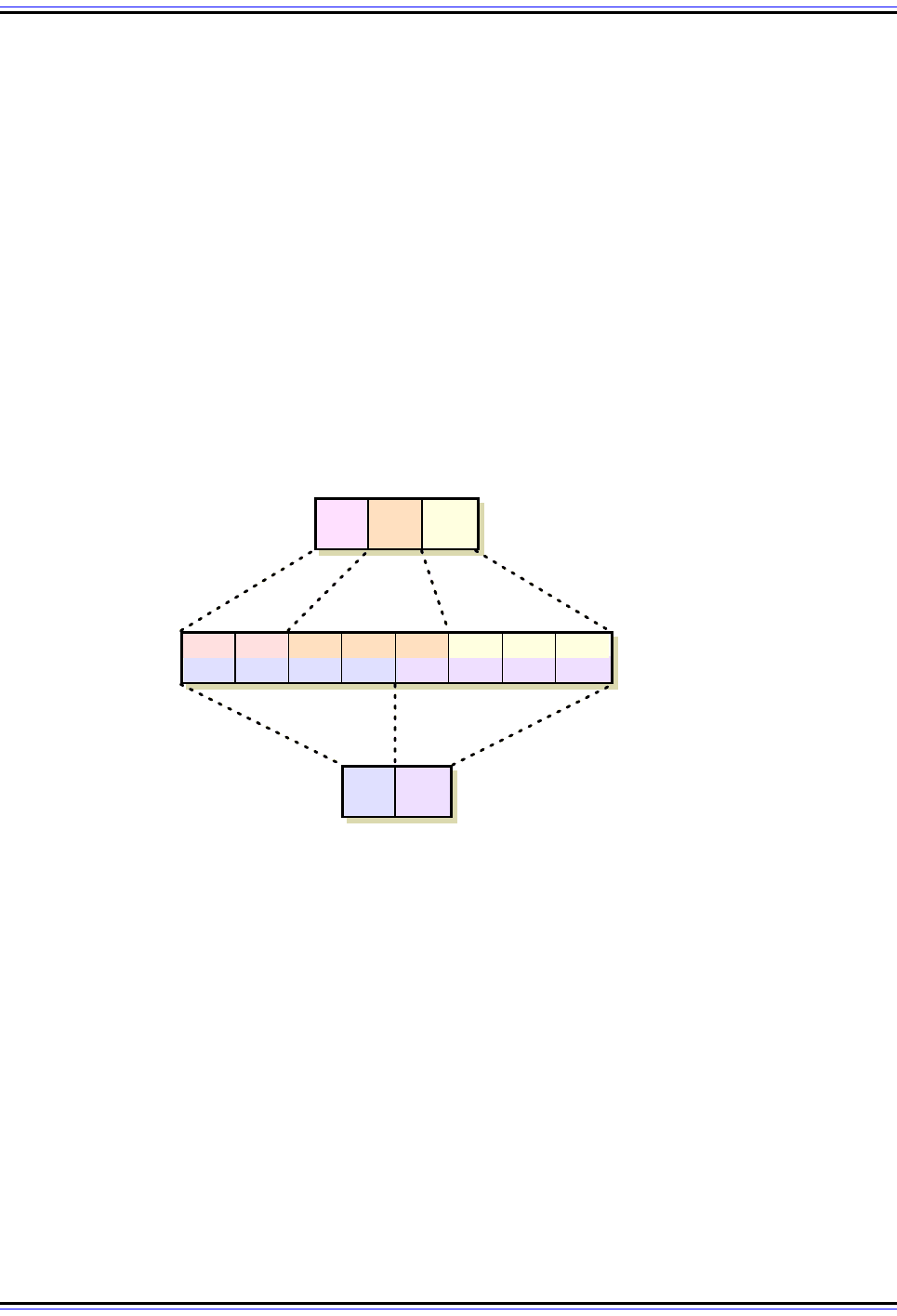
The TCP/IP Guide - Version 3.0 (Contents) ` 125 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
11110100001001000000 in binary. To make binary numbers easier to work with, two
different shorthand notations have been defined. In both of these, instead of working with
each bit individually, they are collected into subgroups, each of which is assigned a single
digit in an alternative numbering system.
Octal Numbers
Let's take the binary number 11110100, which is 244 in decimal. Now, instead of looking at
each bit individually, let's chop them into groups of three, starting from the right. So,
11110100 becomes (11)(110)(100). Now, each of those groups has three bits, so each can
have 2
3
values: from 0 to 7. In this case, (11)(110)(100) = (3)(6)(4), or 364 in the octal or
base-8 numbering system (see Figure 9). Just as with binary, octal numbers are the same
as decimal numbers, except they are base 8 instead of base 10. So, 364 in octal is just 3
times 64 plus 6 times 8 plus 4, or 244. The advantage that octal has over binary is obvious:
it's a lot less cumbersome to deal with larger numbers. 1,000,000 in decimal is 3641100 in
octal.
Hexadecimal Numbers
Octal numbers were at one time quite commonly used, but are much less popular today.
The problem with octal is that it divides bits into groups of three, but sets of binary numbers
typically use a number of bits that is a multiple of four. An alternative method was defined
that does the same thing but using groups of four. Since there are four bits in each group,
each can have one of sixteen values, and this is called the hexadecimal or base 16
numbering system. It is also commonly called just hex for short.
Figure 9: Binary, Octal and Hexadecimal Number Representations
A binary number can be represented in octal form by grouping its bits into sets of three, or in hexadecimal by
using sets of four bits. These base-8 and base-16 numbers have the advantage of being far shorter than
binary numbers, and hence much easier to work with.
11110100
3 6 4
F 4
Binary
Hexadecimal
Octal

The TCP/IP Guide - Version 3.0 (Contents) ` 126 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
Note: As an interesting “sidebar”, the term hexadecimal was not the first one used
for base-16 numbers in computing. Originally, these were called sexadecimal
numbers. This is actually the correct term, since Latin prefixes (sexa-) are normally
used for numbers, not Greek ones (hexa-). However, in the early 1950s, IBM decided that
the word “sexadecimal” was just a little too “provocative” for their tastes, so they changed it
to hexadecimal. IBM being IBM—especially back then—meant everyone else followed suit.
As I understand it, neither term is etymologically perfect, but well, this note is long enough
already. ☺
Now, let's go back to the example just above, 11110100 in binary, 244 in decimal. We divide
this into groups of four, to get (1111)(0100). The binary value “1111” is 15, and “0100” is four,
so we have (15)(4). Hmm, now we have a bit of a problem, don't we? We need to be able to
represent “15”, but we only have 10 numerals. To get around this, in hexadecimal numbers
the values 10, 11, 12, 13, 14, or 15 are represented by the letters “A”, “B”, “C”, “D”, “E” and
“F” respectively. So, 11110100 in binary is (15)(4), or “F4” in hexadecimal (also shown in
Figure 9).
Hexadecimal numbers are in some ways even less intuitive than binary ones. After all, it
takes some practice to get used to thinking of letters as numbers. However, they are very
useful due to the way they compactly represent binary information. Where 1,000,000 in
decimal is 11110100001001000000 in binary, it is only “F4240” in hexadecimal—even
shorter than the decimal number, since 16 is larger than 10. Also, a single byte has eight
bits, so it can be represented using only two hexadecimal digits. Due to this convenience
factor, hex numbers are widely used in the field of computing, including networking. For
example, you will often see values expressed in hexadecimal for items such as MAC
addresses, and for representing different types of information in frame or packet formats.
Key Concept: Regular numbers are called decimal numbers because they are built
upon our base-10 system of mathematics. Computers use collections of one-or-zero
bits called binary numbers, which can be treated just like regular numbers except
that each digit can only be 0 or 1 instead of 0 to 9. Bits in a binary number can be expressed
as octal numbers by grouping three bits into an octal digit that ranges from 0 to 7, or taking
sets of four bits to create a single hexadecimal digit from 0 to 15. To represent the values 10
through 15 in hexadecimal using a single character, the letters A through F are used.
If you see a number that has a letter from “A” to “F” in it, you know it is a hex number, but
not all hex numbers have those digits. Hex numbers are usually displayed in a special
notation, to avoid confusing them with decimal numbers. That notation is either a prefix of
“0x” or a suffix of “h” (sometimes both). Thus, the number “54” is just “54”, but “0x54” is “54”
in hexadecimal, which is 5 times 16 plus 4, or “84” in decimal. Be sure to watch for these
representations.
The TCP/IP Guide - Version 3.0 (Contents) ` 127 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
Decimal, Binary, Octal and Hexadecimal Number Conversion
Humans are accustomed to dealing with decimal numbers, while computers use binary
digits. Octal and hexadecimal numbers are “short forms” for binary numbers, where each
hexadecimal digit takes the place of either three or four binary digits. Since people and
computers speak different “number languages”, it is often necessary to convert numbers
from one of these systems to the other. If you spend any amount of time dealing with
computers or networks, you will find yourself needing to do this on occasion, so it's worth
taking a quick look at how it is done.
First of all, let me say this: the easiest way to convert between decimal, binary, octal and
hexadecimal numbers is to use a scientific calculator. This is what most people do, and I
highly recommend it. However, there are cases where you may need to be able to do this
by hand—we don't all always have a calculator on us. Also, understanding the manual
conversion process will help you comprehend more intuitively how binary, octal and
hexadecimal numbers work. So, let's take a look.
Note: If you don't have a scientific calculator, there is a reasonable facsimile built
into most versions of Windows: the Calculator program, which can usually be
found in your Accessories folder. Open it, go to the View menu, and change the
setting from “Standard” to “Scientific”. Click the button next to a numbering system. Then
enter a number, and if you click a button next to a different numbering type, the number will
be converted for you. Easy. (I would bet Apple and UNIX machines have similar tools, I just
have more experience with Windows.)
Conversions Between Binary, Octal and Hexadecimal
Okay, let's start with the easy stuff first. Conversion between binary, octal and hexadecimal
is very simple, as you may have noticed in the preceding topic, where I introduced them.
Each octal digit is three binary digits, and each hexadecimal digit is four binary digits. Thus,
to convert from binary to octal or hex, just group the digits, and convert each group into an
octal or hex digit. To go the other way, convert each hex or octal digit into a set of bits. Table
4 shows the conversions from each of the octal and hexadecimal single-digit values to
binary (with decimal digits thrown in for convenience):
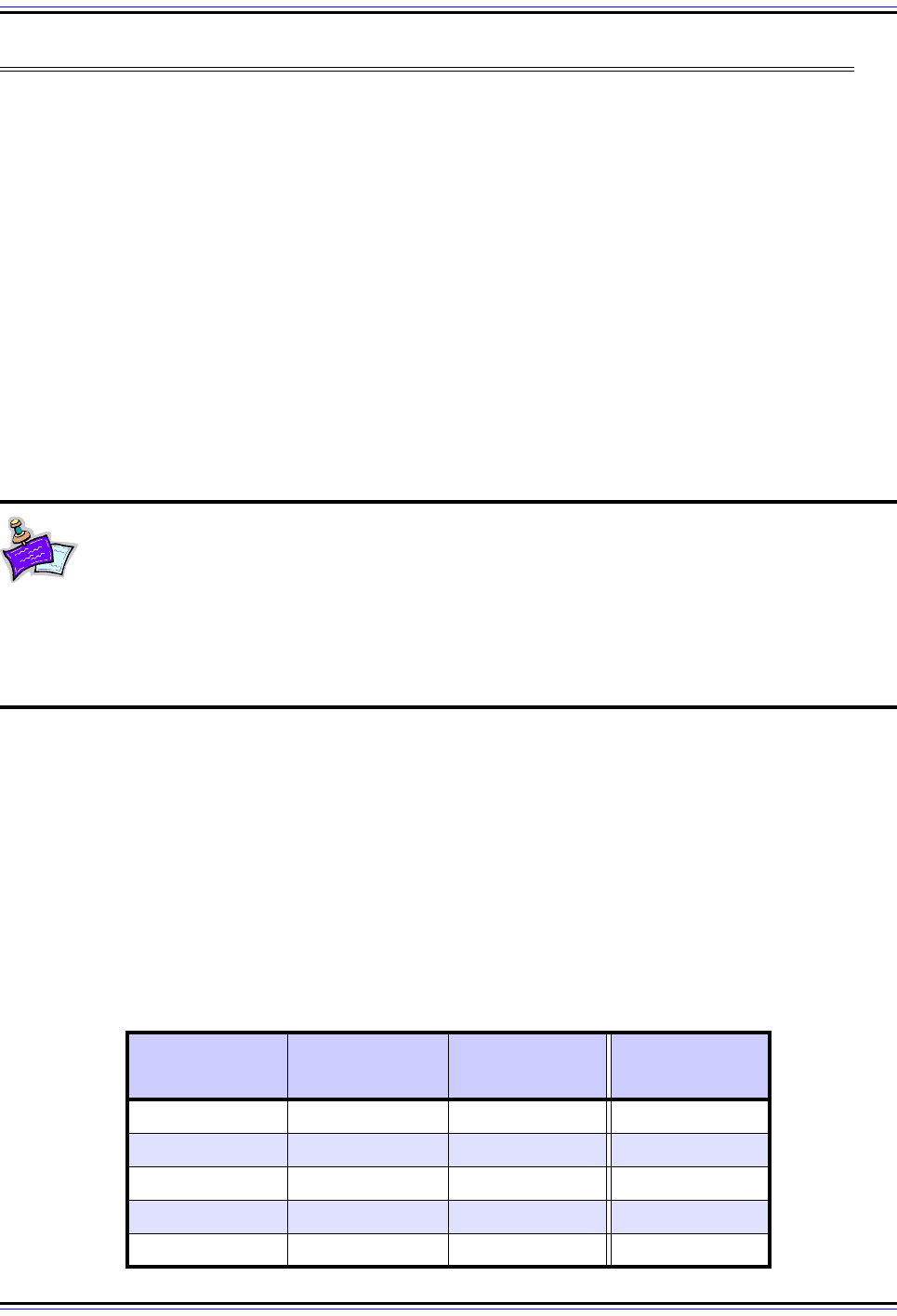
Table 4: Binary, Octal and Hexadecimal Digit Conversion (Page 1 of 2)
Binary Digits Octal Digit
Hexadecimal
Digit
Decimal Digit
0000 0 0 0
0001 1 1 1
0010 2 2 2
0011 3 3 3
0100 4 4 4

The TCP/IP Guide - Version 3.0 (Contents) ` 128 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
Let’s look at some specific examples using larger numbers:
☯ Binary to Octal: Suppose we start with the binary number 110101001010. We divide
this into groups of three: (110)(101)(001)(010). Each of these, we convert to a number
from 0 to 7 (which is easy to do in your head if you practice a bit). The result is
(6)(5)(1)(2) or 6512 octal.
☯ Hexadecimal to Binary: Let's start with the hex number 0x4D1B. We convert each
digit as given in the table above. So, we have 0x4D1B = (0100)(1101)(0001)(1011) or
0100110100011011.
Conversions From Binary, Octal and Hexadecimal to Decimal
Conversions to and from decimal are more complicated than conversions between binary,
octal and hexadecimal, because 2, 8 and 16 are powers of two but ten is not. Of the two
directions, conversions to decimal are easier: you take the value of each binary, octal or
hexadecimal digit, convert it to decimal, and then multiply it by the power of 2, 8 or 16 repre-
sented by the digit's place in the number. Then you add all the numbers together. I did this
in the previous topic with the example of the decimal number 211 (see Table 3).
Let’s take an example of going from hexadecimal to decimal. Table 5 shows the
hexadecimal number 0x830C converted to decimal (octal uses a similar process). Read the
table from left to right, top to bottom; each digit’s value is multiplied by the appropriate
power of 16 and added together, yielding the result 33,548 decimal.
0101 5 5 5
0110 6 6 6
0111 7 7 7
1000 8 8
1001 9 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
Table 5: Hexadecimal to Decimal Number Conversion (Page 1 of 2)
Hexadecimal
Number
830C
Decimal Value of
Digit
8 3 0 12
Table 4: Binary, Octal and Hexadecimal Digit Conversion (Page 2 of 2)
Binary Digits Octal Digit
Hexadecimal
Digit
Decimal Digit

The TCP/IP Guide - Version 3.0 (Contents) ` 129 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
Conversions From Decimal to Binary, Octal and Hexadecimal
Now let’s consider conversions from decimal. These require that you perform the opposite
of the calculation above: you divide and subtract instead of multiplying and adding.
Conversion From Decimal to Binary
The easiest of the three conversions from decimal is to binary—since the maximum value
of each digit is one, there is no dividing, just subtraction. All you do is the following:
1. Find the largest power of two that is smaller than the number.
2. Put a “1” in the digit place for that power of two and subtract that power of two from the
decimal number.
3. Repeat steps #1 and #2 until you are reduced to zero.
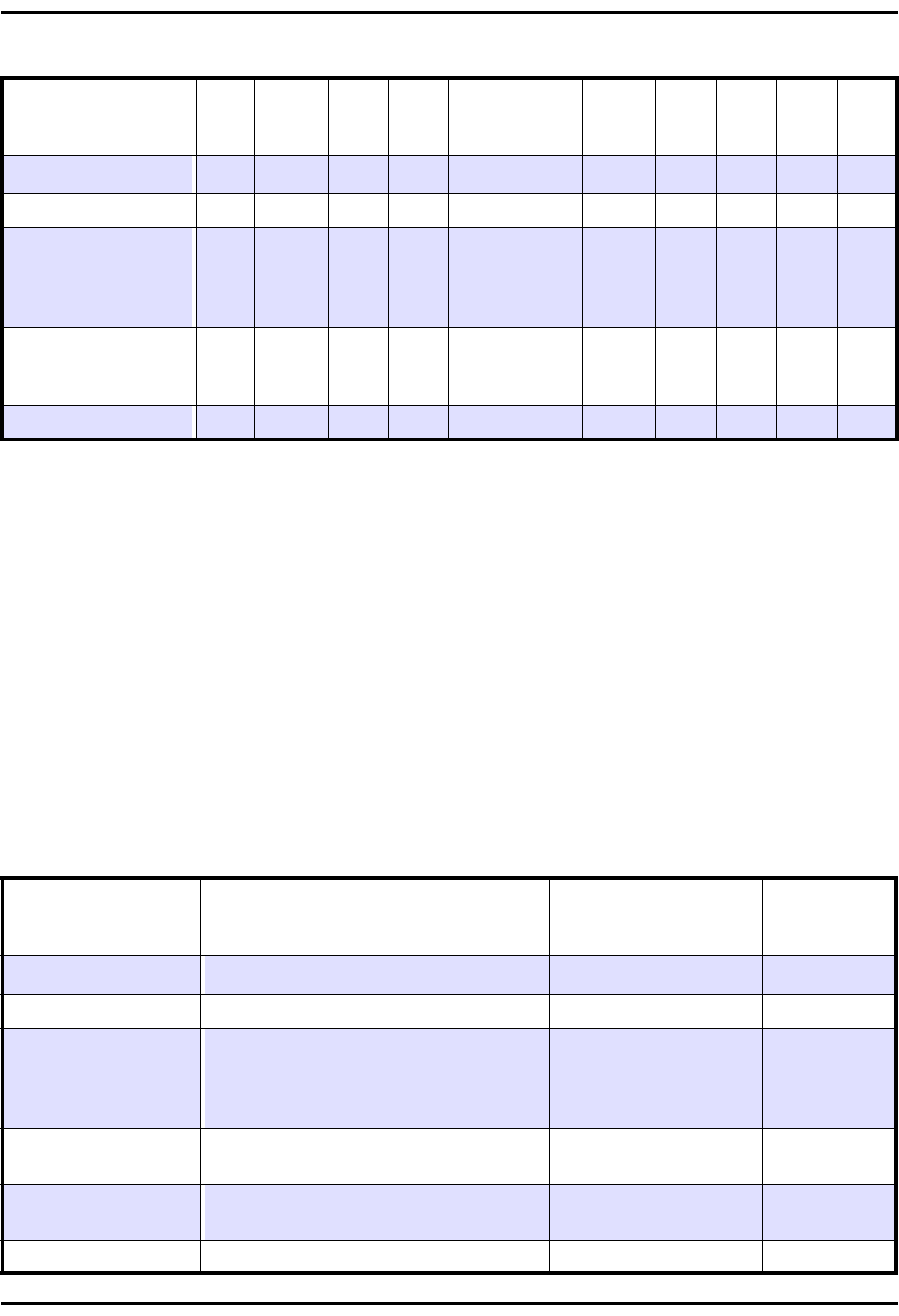
This is easier to explain using an example and a table, of course. Let's convert the decimal
number 689, as shown in Table 6. Again, read the table starting from the upper left, and
going down and then across. We start by noticing that 1024 is not less than or equal to 689,
so the “1024s” place gets a 0. In the next place, 512 is less than 689, so we make the
“512s” place a 1 and subtract 512 from 689 to leave 177. The calculation continues,
eventually showing shows that 689 decimal is 1010110001 binary.
Power of 16
16
3
16
2
16
1
16
0
Value of Digit Place 4096 256 16 1
Value For This
Number
4096*8 = 32768 3*256 = 768 0*16 = 0 12*1 = 12
Running Sum (from
left to right)
32768 32768+768 = 33536 33536 33536+12 = 33548
Table 5: Hexadecimal to Decimal Number Conversion (Page 2 of 2)
The TCP/IP Guide - Version 3.0 (Contents) ` 130 _ © 2001-2005 Charles M. Kozierok. All Rights Reserved.
Conversion From Decimal to Octal or Hexadecimal
The process for octal and hexadecimal is almost the same, except you must divide by
powers of two instead of just subtracting:
1. Start with the highest power of 16 (hexadecimal) or 8 (octal) that is smaller than the
number.
2. Divide the decimal number by that power, keeping only the integer part of the result.
3. Keep the remainder after the division is done, for the next step.
4. Repeat steps #1 to #3 until you get to the “ones” place, and then put there whatever is
left after the higher digits were done.
Table 7 shows the same example as Table 6 but goes from decimal to hexadecimal instead
of decimal to binary: 689 in decimal is 0x2B1 hexadecimal.
Table 6: Decimal to Binary Number Conversion
Decimal Value
Before Considering
This Digit Place
689 6891771774949 171111
Power of Two
2
10
2
9
2
8
2
7
2
6
2
5
2
4
2
3
2
2
2
1
2
0
Value of Digit Place 10245122561286432 168421
Value of Digit Place
Equal To or Less
Than Current
Decimal Number?
No Yes No Yes No Yes Yes No No No Yes
Subtraction Step skip
689-
512 =
177
skip
177-
128
= 49
skip
49-32
= 17
17-16
= 1
skip skip skip
1-1 =
0
Binary Digits 0 1 0 1 0 1 1 0 0 0 1
Table 7: Decimal to Hexadecimal Number Conversion
Decimal Value
Before Considering
This Digit Place
689 689 177 1
Power of 16
16
3
16
2
16
1
16
0
Value of Digit Place 4096 256 16 1
Value of Digit Place
Smaller Than
Current Decimal
Number?
No Yes No n/a
Division Step skip
689/256 = 2.691;
use “2” for this digit.
177/16 = 11.0625;
use “B” for this digit.
n/a
Remainder After
Division
skip 177 1 n/a
Hexadecimal Digits 0 2 B 1
