Casing/Tubing design manual october 2005 Chevron

Подождите немного. Документ загружается.

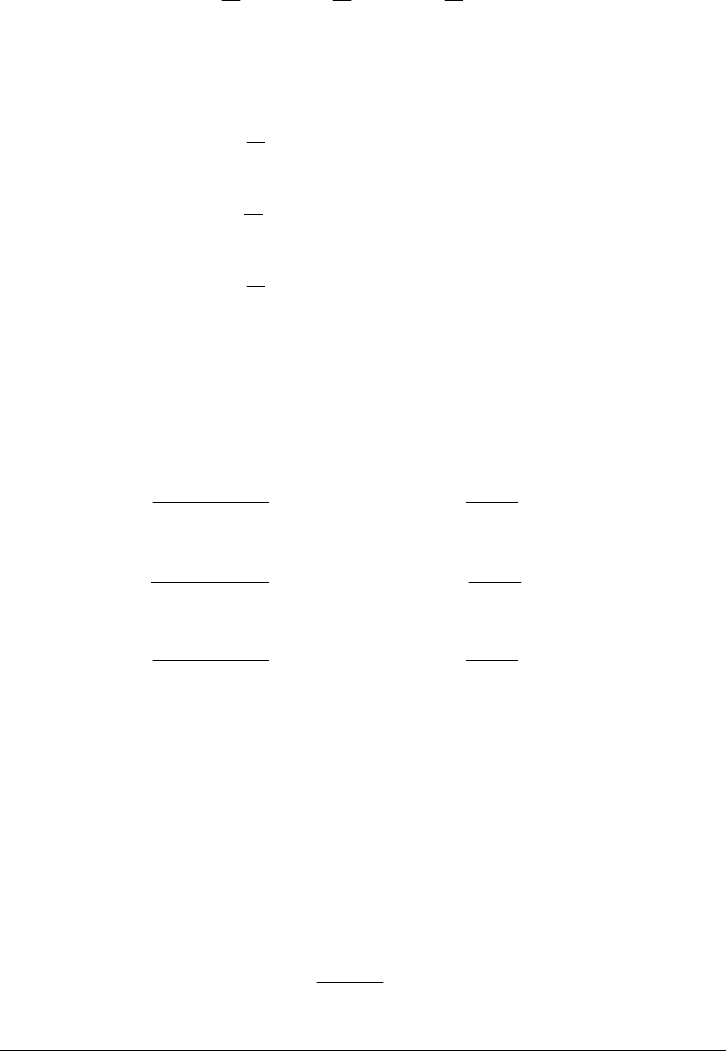
between the two being yield. For multiple dimensions, however, the yield stress

will now be replaced by a multi-dimensional yield surface.

D.5.1 Elastic Behavior

As long as the response of the steel is elastic, the contributions to strain of the

various stress components may be superimposed. For example, and recalling

equations (D-38) and (D-39), an imposed axial stress,

, will result in the

following strains,

εσε

σε

zzr z

==−=−

(D-53)

Generalizing equation (D-53) for a multi-dimensional loading by superimposing

the effects of all normal stress components,

()

[]

εσµσσα

rr z

T=−++

∆

(D-54)

()

[]

εσµσσα

θθ

=−++

∆ (D-55)

()

[]

εσµσσα

zzr

T=−++

∆

(D-56)

where, in addition, the effect of a temperature change,

∆

, has been included,

being the coefficient of linear expansion.

Equations (D-54) through (D-56) can be solved simultaneously for

yield:

()( )

()

[]

µµ

µε µε ε

rrz

+−

−++−

−112

∆

(D-57)

()( )

()

[]

µµ

µε µε ε

θθ

+−

−++−

−

112

∆

(D-58)

()( )

()

[]

µµ

µε µε ε

zzr

+−

−++−

−112

∆

(D-59)

The relations between shear stresses and shear strains are:

(D-60)

rz rz

(D-61)

(D-62)

where:

()

+21

(D-63)

D-22 Casing/Tubing Design Manual

October 2005

Temperature changes have no effect on shear deformations.

D.5.2 Plastic Behavior

The behavior of ductile solids beyond the elastic limit or yield stress is not

completely understood, even for relatively simple solid materials such as steel.

For this reason, and in order to remain within the scope of this discussion, the

simplest of the recognized theories will be considered

D.5.3 Yield Condition

The first step in describing a material that has the potential to exhibit plastic

behavior is to arrive at a criterion of yield, that is, a condition that marks the onset

of plastic behavior. This criterion is normally expressed in terms of a yield surface

plotted in a coordinate system, or stress space, whose axes are the components

of stress.

Figure D-8 illustrates the relation between the yield surface in uniaxial and multi-

dimensional states of stress. When only one stress component is nonzero, for

example, in a uniaxial tension test, the stress space is a line. All the information

necessary to describe yield of the material can be plotted on the

-axis, the

initial yield “surface,” for example, being a point on the

-axis denoted in the

figure by

. For multi-dimensional loading, the stress space becomes multi-

dimensional, and the yield condition is represented by a surface. The exact

nature of the shape of this yield surface will depend upon the material.

For a more complete treatment of inelastic behavior, the interested reader is referred to

Fung [1965] and Kachanov [1971].

Casing/Tubing Design Manual D-23

October 2005

= σ

σ’

Work Hardening

Perfect Plasticity

von Mises

Tresca

= σ

π−plane

a. One-dimensional loading b. Multi-dimensional loading

Figure D-8. Initial Yield in One-Dimensional and Multi-Dimensional Stress Spaces

To obtain some feel for the shape of the multi-dimensional yield surface, consider

either (1) a loading for which all shear stresses on the coordinate faces vanish, or

(2) a general stress state for which the local axes have been rotated to coincide

with the directions of principle stress

. An example of a multi-dimensional

loading that produces no shear stress along the

, r

, coordinate directions

would be the application of internal or external pressure to a long tube.

Because all shear stresses vanish for either of the stress states described above,

the stress space is three-dimensional with the three axes corresponding to the

three normal stresses. The consequences of available experimental data on the

shape of the yield surface for metals are as follows:

• Yield is independent of mean normal stress – As a consequence of this

observation, the yield function describing the initial yield surface will be

independent of

123

. Geometrically this condition implies

that the yield surface, when plotted in principle stress space, will be a

cylinder (not necessarily circular) perpendicular to the plane

123

0++= as indicated in Figure D-8b.

The concept of principle stresses, that is, expression of the stress tensor in a coordinate

system aligned such that all shear stress components vanish, is related to the more general

topics of matrix transformations and matrix invariants. The interested reader is directed to

Fung [1965] and Kachanov [1971].

D-24 Casing/Tubing Design Manual

October 2005

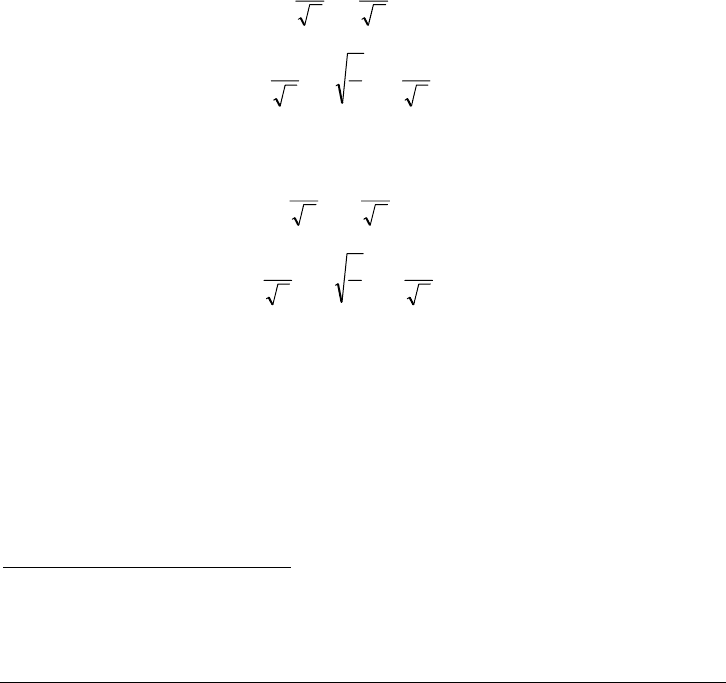
• Additional experimental data – Apart from the simplification outlined

above, various authors have proposed a variety of cylindrical cross

sections as suitable descriptions of material yield. Fortunately, two of the

simplest proposals have also proven to be the most reliable in

reproducing experimental observation. Consider a plane (called the -

plane) that intersects the yield cylinder perpendicularly to present an

undistorted view of the cylinder cross section. The two yield functions,

named after their authors are:

o Tresca’s yield function – Tresca’s yield criterion, also known as the

condition of maximum shear stress, results in a cylinder whose cross

section is a hexagon. In simplest terms, Tresca’s condition states

that the material will yield when the maximum shear stress on any

plane through a given point reaches a certain critical value.

o von Mises’ yield function – von Mises’ yield criterion, also known as

the condition of maximum distortional energy, results in a cylinder

whose cross section is circular. One statement of von Mises’

condition is that yield will occur when the maximum shear stress in

the

π-plane reaches a certain critical value.

We can now use the characteristics of the initial yield surface discussed above to

formulate an equation for multi-dimensional yield

. Figure D-9 shows a new

coordinate system (

, ξ

) in the π-plane. Unit vectors and

along these

coordinates can be written in terms of unit vectors along the

, σ

axes,

=−i

(D-64)

eii

~~~

212

=− + −

(D-65)

which implies the following relations between coordinates,

ζσ

=−

(D-66)

ζσσ

212

=− + −

(D-67)

Here, we will restrict ourselves to the von Mises yield condition. Because of its

mathematical simplicity, this yield function will be used almost exclusively in this text

when multi-dimensional loading is under consideration.

Casing/Tubing Design Manual D-25

October 2005

= σ

, ζ

are in π-plane

Figure D-9. Coordinate System for Defining von Mises Yield Surface for

Axisymmetric Deformation

Writing the equation for the von Mises yield condition in the π-plane,

ζζζ

(D-68)

where

is the radius of the cylinder, and using equations (D-66) and (D-67) in

(D-68), the expression for the von Mises yield criterion in stress space is:

()

12 13 23

σσσσσσσσσ ζ

++− − − =

(D-69)

The radius,

, can be found by realizing that in the special case of uniaxial

loading,

0==, and equation (D-69) reduces to:

σσ

(D-70)

at first yield, implying:

(D-71)

In other words, the radius of the yield cylinder is simply 23 times the yield

stress in a uniaxial tension test.

The final form of the von Mises yield condition for axisymmetric loading of a tube

is therefore:

σ σ σ σ σσ σσ σσ

12 13 23

=++− − −

(D-72)

Before continuing, it is important to emphasize that the derivation of the initial

yield condition leading to equation (D-72) was based in large part on heuristic

D-26 Casing/Tubing Design Manual

October 2005

arguments and simple manipulations in solid geometry. This approach certainly

does not do justice to the volumes of literature available on material yield.

Nevertheless, this text is not intended to be a treatise on inelastic material

behavior. The material presented above, although superficial, is by no means

incorrect and the primary purpose of this section will be fulfilled if the reader is

left with some general concept of the yield surface in multi-dimensional stress

space.

D.5.4 Hardening Law

The discussion of the previous section was directed at predicting the onset of

material yield or plastic behavior. It now becomes important to investigate the

behavior of a material in instances where the stress state continues to be

increased in such a manner as to exceed initial yield. It is, again, instructive to

begin with an analysis of uniaxial behavior. Consider Figure D-8a once more and

now let it be assumed that after the initial yield stress has been reached, the

external tensile load is increased further to a stress level equal to

′

. Now, let

the external tensile load be removed completely. As a consequence of the

loading sequence described above, a “new” material has been created with the

following characteristics:

• An internal, residual strain,

, in the unloaded state

• Elastic material behavior for all tensile stresses less than

′

• Plastic material behavior for stresses greater than

′

• A lower compressive yield stress

It now becomes necessary to translate these one-dimensional observations into

multi-dimensional generalizations.

D.5.4.1 Residual Strain

In stress space the residual strain does not appear explicitly. Consideration of

residual strain is beyond the current scope of this text.

D.5.4.2 Elastic Behavior

In multi-dimensional stress space, points on the interior of the yield surface are

considered to be governed by elastic behavior. The interior of the yield surface

corresponds to the one-dimensional stress range

(

)

′

≤≤

′

σσσ

yc y

D.5.4.3 Alteration of the Initial Yield Condition

According to the most commonly applied plasticity theories, stress states in

excess of or exterior to the current yield surface are not permitted. Rather, once

the stress path reaches the yield surface, any further increase in loads is

accompanied by a corresponding change in the yield surface. For a one-

dimensional stress state, for example, the loading of Figure D-8a, the change in

the yield surface is primarily represented by a change in the tensile yield stress

from

′

; however that is not all. A large body of experimental observation

Casing/Tubing Design Manual D-27

October 2005

indicates that the entire yield surface is affected by plastic deformation. In terms

of uniaxial loading, this associated effect on the entire yield surface may be

described by studying the effect of plastic deformation under tensile loading on

the compressive yield stress.

To this point, no mention has been made of the behavior of a ductile material in

compression. In terms of uniaxial loading, it is generally acceptable to state that

the initial compressive yield stress is equal in magnitude to the initial tensile yield

stress. However, as indicated in Figure D-8a, tensile yield will not only alter the

tensile yield stress, but may also alter the compressive yield stress. This lowering

of the compressive yield stress associated with tensile yield is called the

Bauschinger effect.

Table D-3. Hardening Laws

Type of Hardening One-Dimensional Effect on Yield

Surface

Multi-Dimensional

Generalization

Kinematic

Tension

→

′

Compression

(

)

′

−

σσ σσ

yc yc y y

Translation of yield

surface

Isotropic

Tension

→

′

Compression

yc y

→

′

Expansion of yield

surface

Initial Yield Surface

= σ

b. Isotropic hardening

(yield surface expands)

= σ

a. Kinematic hardening

(yield surface translates)

σ’

Initial Yield Surface

Subsequent Yield Surface Subsequent Yield Surface

Figure D-10. Illustration of Hardening Laws in One- and Multi-Dimensions

In very simplified terms, the two most popular methods of modeling movement of

the yield surface because of loading beyond initial yield are described in Table D-

3 and depicted pictorially in Figure D-10. In reality, carefully conducted

D-28 Casing/Tubing Design Manual

October 2005

experiments have indicated that change of the initial yield surface can be a

combination of translation, expansion/contraction, and local distortion. However,

to date, no generally accepted description of the alteration of the initial yield

surface has been presented in the literature.

In this text, all future work will be conducted using the assumption of isotropic

hardening. Although isotropic hardening may not provide as good a model of

material behavior as kinematic hardening, this shortcoming is outweighed by the

mathematical simplicity of the isotropic model. For the von Mises yield function,

isotropic hardening implies an expansion of the yield surface then the effect of

hardening may be incorporated into the yield condition by altering equation (D-

72) to the form:

σ σ σ σ σσ σσ σ σ

12 13

=++− − ≥

(D-73)

where

′

is the maximum value of

attained in the loading history. Notice that

initially,

′

, and in the presence of inelastic deformation

′

can only

increase. Also notice that for the special case of ideal or perfectly plastic

behavior,

′

Cons ttan

D.5.5 Flow Rule

The previous two sections presented two important concepts regarding multi-

dimensional elastic-plastic behavior. In the former, the purpose was to delineate

the general characteristics of the initial yield surface describing the onset of

plastic behavior. Following the onset of plasticity, the initial yield surface will

evolve into subsequent yield surfaces, the exact nature of the evolution being

embodied in the hardening law. Given these concepts, and the entire history of

loading up to and including the current state of stress, it is possible to state

conclusively within the confines of the models presented whether the behavior of

the material under the next increment of loading will be:

• Elastic – The stress state is interior to the current yield surface, or in the

one-dimensional case,

′

≤

′

yc y

(see Figure D-8).

• Elastic-Plastic Loading – The stress state is coincident with a point on

the current yield surface and the next increment of load is directed

toward the exterior of the yield surface. In the one-dimensional case,

either

′

with d

> 0 or

′

with d

• Elastic-Plastic Unloading (Elastic Behavior) – The stress state is

coincident with a point on the current yield surface and the next

increment of load is directed toward the interior of the yield surface. In

the one-dimensional case, either

′

with d

0 or

′

with

> 0.

• Elastic-Plastic Neutral Loading – The stress state is coincident with a

point on the current yield surface and the next increment of load is

directed along the tangent to the yield surface. In the one-dimensional

case, either

′

with d

Casing/Tubing Design Manual D-29

October 2005

The conclusion reached is that the history of loading, when plotted in stress

space, is sufficient to determine the type of behavior expected from the material

during the next load increment. However, our quantitative description of material

response is still incomplete. In particular, no mention has yet been made of the

constitutive response of the material in the event that any portion of the loading

history involves plastic deformation. In other words, in conjunction with the

loading path plotted in stress space, there exists a corresponding path in strain

space which also deserves attention.

Provided the loading history is such that the initial yield surface is never

penetrated, that is, in the absence of plastic loading, the response of the material

will be described by the elastic constitutive equations. However, for any

increment of load involving plastic deformation, the constitution of the material is

effectively altered and a new set of stress-strain relations must be developed. In

particular, a flow rule must be introduced to determine the plastic or irrecoverable

part of the strain associated with plastic behavior.

As long as the discussion is restricted to infinitesimal strains, the total strain in

the plastically deformed body can be decomposed into elastic and plastic parts,

εεε ε ε ε

θθθ

=+ = +,... ,...,

(D-74)

where

()

denotes the elastic component and

(

)

denotes the plastic

component. The elastic components of strain are related to the current stress

state by equations (D-54) though (D-56) and (D-60) through (D-62). The

constitutive equations for the plastic strain components have historically been

determined by two alternative approaches:

• Deformation Theory – This theory proposes a relationship between total

strain and stress. Although this model lacks a firm theoretical

justification, the deformation theory has found application in many simple

problems in which load reversals (retracing a portion of the stress path)

are unanticipated. Additionally, although no suitable explanation has

appeared in the literature, the deformation theory is more accurate than

the more theoretically sound incremental theory in certain stability

analyses.

• Incremental Theory – The incremental theory of plasticity envisions a

relationship between an increment in plastic strain and stress. Within the

current state of the art of plasticity theory, the incremental theory

possesses a firm theoretical foundation. In complex loading paths

involving stress reversals, and if a bifurcation type stability analysis is not

under consideration, the incremental theory is to be preferred over the

deformation theory.

In order to quantify plastic flow for multi-dimensional stress states, let us first

rewrite the current yield condition as:

=++− − − −

′

σ σ σ σσ σσ σσ σ

12 13 23

(D-75)

The behavior of a material point can now be categorized mathematically as:

D-30 Casing/Tubing Design Manual

October 2005

f Elastic

f df Unloading

f df Neutral loading

f df Loading

(D-76)

In other words, incipient yield is characterized by the stress state being in contact

with the current yield surface (i.e.,

), and the question of whether the next

increment of load will produce any additional plastic deformation is determined by

the direction of the increment with respect to the yield surface (i.e.,

Notice that the condition

is not recognized in equation (D-76). Whenever

plastic loading occurs, the yield surface will expand to maintain the condition

f > 0

f = 0

Our remaining task is to arrive at an expression for the plastic strain increment

associated with plastic loading

. Derivation of the equations for plastic strain

increment is beyond the scope of the main body of this text. Here we will present

the final forms of the plastic strain increment relations for future reference.

Let us introduce the function

, where

for

fdf

>0, 0

and

= 0

for

or . Additionally, let us restrict our attention to load paths where the

shear stresses

f < 0 df < 0

θθ

rrzz

0 then

θθ

rrzz

0 as do both the elastic

and plastic contributions to these total strains. The remaining increments in

plastic strain are:

dCdCdCd

rr r r rz z

rr zz

zr r z zz z

εσσσ

εσσ

εσσσ

θθ

θθ θθθθ

θθ

=++

(D-77)

where, for the deformation theory of plasticity,

The other possibilities of elastic behavior (

) and unloading ( ) from a

current plastic state produce no increment in plastic strain.

df < 0

Casing/Tubing Design Manual D-31

October 2005