Casing/Tubing design manual october 2005 Chevron

D.1 Introduction

The purpose of this appendix is to introduce most of the equations necessary to

the study the response of a tubular structure to external loads. The majority of

the discussion will be centered on axisymmetric deformation of a thick cylinder.

However, because of their importance to tubular design, the necessary

approximations leading to the equations for a thin cylinder will also be discussed.

Not covered here are the specific relations for stability type failures. These

relations will be detailed in the discussions of collapse and column stability.

Although every effort was made to ensure that the forthcoming derivations are

complete and self-contained, it is presumed that the reader has a background in

such basic concepts as stress and strain. Other terms falling outside the scope of

an introductory level course in mechanics of materials will be explained at the

time they are introduced.

Due to the geometric shape of oil field tubulars, all analyses will be carried out in

cylindrical (

r ,

θ

, ) coordinates. z

D.2 Strain-Displacement Relations

In the analysis of any solid body, three concepts are of paramount concern –

stress, strain, and the constitution of the material that permits one to relate stress

and strain. Both stress and strain are independent of the material constitution:

• Stress, regardless of the material being studied, is strictly determined by

the applied loads.

• Strain is strictly concerned with the kinematics of the deformation.

The character of the material being studied only appears when one relates stress

(loading) to strain (response) via appropriate constitutive equations.

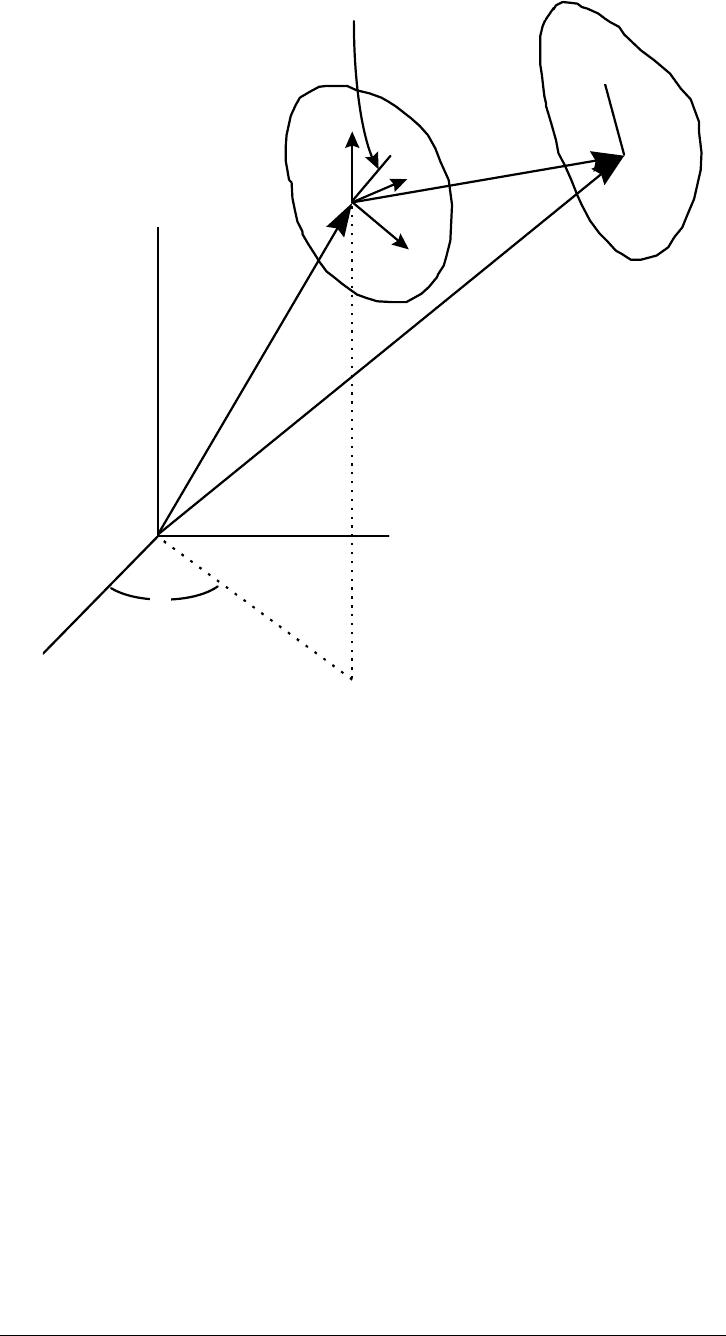
Figure D-1 depicts the translation, rotation, and deformation of a body in

response to some unknown set of applied forces. We desire to develop a general

expression for the local deformation at any point in the body. In particular,

consider an infinitesimal line element bounded by Points 1 and 2. Because of

deformation, Point 1 in the original configuration will be displaced to Point 1' in

the deformed configuration. The position vector,

, of the deformed location of

Point 1 can be written:

s

~

'

z

r

isisiss

~~~~

''''

+

=

θ

(D-1)

D-2 Casing/Tubing Design Manual

October 2005

2

2’

1

1’

ds’

ds

Z

Undeformed

Configuration

Deformed

Configuration

Y

r

X

θ

s

~

s’

~

u

~

i

~z

i

~r

i

~θ

Figure D-1. Deformation of an Infinitesimal Line Element

or, alternately,

ssu

sui sui

sui

rr

r

zz

z

~~~

~~

~

'

()()

()

=

+

=+ ++

++

θθ

θ

(D-2)

where is the original position of Point 1, is the displacement at Point 1, and

, , are unit vectors in the ,

s

~

u

~

i

r

~

i

~

θ

i

z

~

r

θ

, directions, respectively, the unit

vectors being referenced to the original, undeformed configuration.

z

An infinitesimal line segment,

, in the undeformed configuration will, because

of applied loads, be translated, rotated, and deformed into an infinitesimal line

segment,

, in the deformed configuration. For example, the segment 1-2 in

Figure D-1 will be transformed into the segment 1'-2'. Our concern is to arrive at

a description of the transformation from segment 1-2 to segment 1'-2' that

isolates the portion of the motion because of deformation of the segment and

ignores the rigid body terms (i.e., translation and rotation). This local description

of material distortion is the essence of the concept of strain.

ds

ds'

Casing/Tubing Design Manual D-3

October 2005

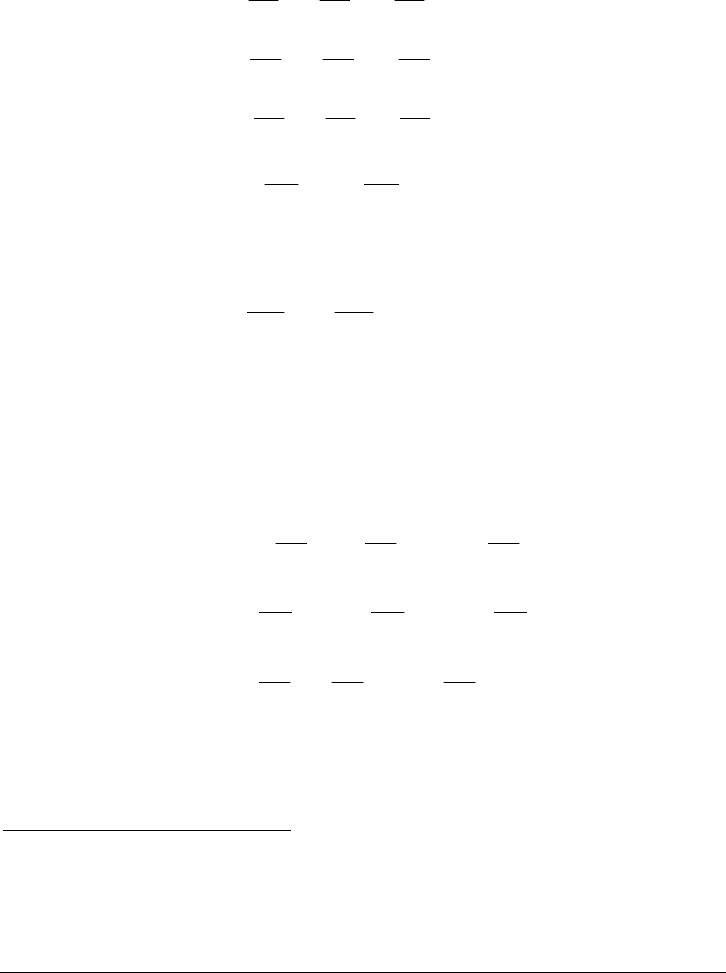
Quantitatively, strain is defined as the change

1

( )

ds'

2

-( )

ds

2

where is the

magnitude of

and

ds

is the magnitude of [Eringen, 1967]. From equation

(D-2),

ds'

ds

~

' ds

~

ds ds du

~~

'

~

=

+

(D-3)

where,

ds ds i ds i ds i

dr i rd i dz i

r

z

rz

~~~

~~

=++

=+ +

θ

~

(D-4)

and, by straightforward differentiation,

du

u

r

dr

u

d

u

z

dz i

u

r

dr

u

d

u

z

dz i

u

r

dr

u

d

u

z

dz i

u

i

du

i

d

rr r

r

zz z

z

r

~~

~

=++

⎛

⎝

⎜

⎞

⎠

⎟

+++

⎛

⎝

⎜

⎞

⎠

⎟

+++

⎛

⎝

⎜

⎞

⎠

⎟

++

∂

∂θ

θ

∂

∂θ

θ

∂

∂θ

θ

∂

∂θ

θ

∂

∂θ

θ

θθ θ

θ

(D-5)

The derivatives of the unit vectors are given by,

∂

∂θ

∂

∂θ

θ

i

r

~

,==−

(D-6)

using equations (D-4) through (D-6) in (D-3), the strain measure can be written,

() ()

()

(

)

(

)

()

ds ds ds ds ds

ds ds ds

u

r

dr

u

ud

u

z

dz

u

r

dr r

u

ud

u

z

dz

u

r

dr

u

d

u

z

rz

rr r

r

zz z

′

−= + +

−++

⎡

⎣

⎢

⎤

⎦

⎥

=+

⎛

⎝

⎜

⎞

⎠

⎟

+−

⎛

⎝

⎜

⎞

⎠

⎟

+

⎡

⎣

⎢

⎤

⎦

⎥

++++

⎛

⎝

⎜

⎞

⎠

⎟

+

⎡

⎣

⎢

⎤

⎦

⎥

++++

⎛

⎝

⎜

⎞

⎠

⎟

22

222

2

1

'''

θ

θθ θ

∂

∂θ

θ

∂

∂θ

θ

∂

∂θ

θ

∂

() ( ) ()

[]

dz

dr r d dz

⎡

⎣

⎢

⎤

⎦

⎥

−+ +

2

22

θ

(D-7)

1

If (ds')

2

-(ds)

2

vanishes everywhere within the body, no local distortion has occurred and

the transformation from segment 1-2 to segment 1'-2' can be expressed as a rigid body

motion consisting of a translation of any point P in the body plus a rotation about an axis

passing through point P. The measure of strain given here thus fulfills the requirement of

isolating the portion of motion due solely to deformation of the segment.

D-4 Casing/Tubing Design Manual

October 2005

Multiplying and collecting terms in equation (D-7) leads to a simple, but lengthy,

expression. However, if it is assumed that all of the displacements and

displacement gradients (

∂

ur

r

, etc.) are small, then higher order terms in these

quantities may be neglected, and equation (D-7) becomes:

() () ()

()

ds ds

u

r

dr

u

rr

u

rd

u

z

dz

u

rr

u

r

rdrd

u

r

u

z

drdz

u

zr

u

rdzd

rr

z

rz

z

′

−= ++

⎛

⎝

⎜

⎞

⎠

⎟

+

++−

⎛

⎝

⎜

⎞

⎠

⎟

++

⎛

⎝

⎜

⎞

⎠

⎟

++

⎛

⎝

⎜

⎞

⎠

⎟

22 2

2

22

1

2

1

2

1

∂

∂θ

θ

∂

∂θ

θ

∂

∂θ

θ

θθ

θ

r

θ

(D-8)

The coefficients of the differential products in equation (D-8) have been given

special names and represent the components of strain. Introducing the strain

components in the conventional manner through the expression:

() () ()

()

ds ds dr rd dz

rdrd drdz rdzd

rz

rrzz

′

−= + +

+++

22 2

2

22 2

444

εεθε

εθε ε

θ

θθ

(D-9)

One can, by comparing equations (D-8) and (D-9), arrive at the definitions:

ε

∂

ε

∂

∂θ

ε

∂

εε

∂

∂θ

εε

∂

εε

∂

∂θ

θ

θθ

θ

r

rr

z

rr

r

rz zr

zr

zz

z

u

r

u

rr

u

z

u

rr

u

r

u

r

u

z

u

zr

u

==+ =

== + −

⎛

⎝

⎜

⎞

⎠

⎟

== +

⎛

⎝

⎜

⎞

⎠

⎟

== +

⎛

⎝

⎜

⎞

⎠

⎟

,,

,

.

1

2

1

2

1

2

1

(D-10)

D.2.1 Special Cases

Within the confines of the assumption of infinitesimal displacements and

displacement gradients, the expressions for the components of strain given in

equation D-10 are completely general. However, there exist special displacement

fields having wide application in tubular problems for which the strain-

displacement relations assume simpler forms.

D.2.1.1 Axisymmetric Deformation

If the deformation is symmetric with respect to the -axis (taken to correspond

with the axis of the tube), then the displacement field is independent of

z

θ

implying:

∂

∂θ

∂

∂θ

∂

∂θ

θ

u

r

===0

z

(D-11)

Casing/Tubing Design Manual D-5

October 2005

Furthermore, u

θ

=

0, so that the simplified strain-displacement relations for the

case of axisymmetric deformation become:

ε

∂

ε

∂

ε

∂

εεε

θθθ

r

z

rz

zr

r

rz

u

r

u

z

u

r

u

z

u

r

== =+

⎛

⎝

⎜

⎞

⎠

⎟

===

,,

,.

1

2

0

,

(D-12)

D.2.1.2 Plane Strain

For this simplification, the displacement field is independent of the -coordinate: z

∂

θ

u

z

u

z

u

z

r

===0

z

(D-13)

Furthermore,

, so that the simplified expressions for the strain components

become:

u

z

= 0

ε

∂

ε

∂

∂θ

ε

∂

∂θ

εε ε

θ

θθ

θ

r

rr

r

zrz z

u

r

u

rr

uu

rr

u

r

==+ =+−

⎛

⎝

⎜

⎞

⎠

⎟

===

,,

.

11

2

1

0

,

(D-14)

D.2.2 Physical Interpretation of Strain

Components

The derivation of the strain components given in the previous section is

mathematically clean and straightforward. However, by employing such a general

approach, one is likely to lose sight of the physical meaning of the components of

the strain tensor. In order to gain more insight into the concept of strain, consider

Figure D-2. The figure is drawn for the case of plane strain (

u

z

=

0 ), but this two-

dimensional deformation should be sufficient to display the necessary concepts.

Consider first a differential line segment 1-2 initially lying along a radius that,

because of some unknown external loading, translates, rotates, and deforms (in

this case, stretches) to become the line segment 1'-2' (Figure D-2.a). Let us

calculate the change in length of this line segment. Removing the translation,

which does not affect deformation, the deformed configuration can be

superimposed on the undeformed configuration as shown in Figure D-2.b. During

deformation, Point 1 will displace a distance

in the direction and a distance

in the

u

r

u

θ

direction. Point 2 will displace a distance u

u

r

dr

r

+

∂

in the

direction and a distance

r

u

r

dr

θ

∂

+ in the

θ

direction. As indicated in the figure,

the relative displacement of Point 2 (as compared to Point 1) in the

direction is

therefore

r

∂

u

r

dr

r

. In a similar manner, the relative displacement of Point 2 in the

θ

direction is

∂

θ

u

r

dr . The length of the line segment 1'-2' can now be calculated

as:

D-6 Casing/Tubing Design Manual

October 2005

()

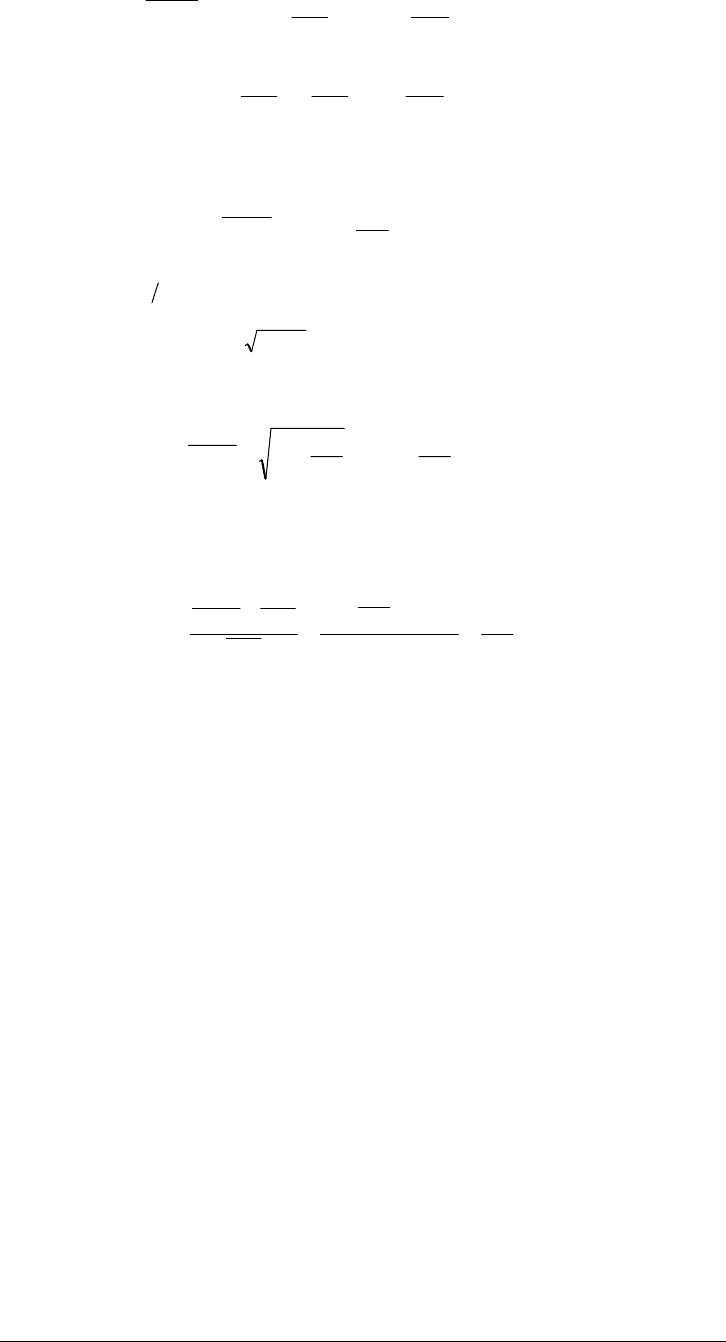
2

21

dr

r

u

r

u

r

u

dr

r

u

dr

r

u

dr

rr

r

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

++=

⎟

⎠

⎞

⎜

⎝

⎛

+

⎟

⎠

⎞

⎜

⎝

⎛

+=

′

−

′

∂

θ

(D-15)

Ignoring the higher order terms in the displacement gradients,

()

′

−

′

=+

⎛

⎝

⎜

⎞

⎠

⎟

12 12

2

∂

u

r

dr

r

(D-16)

Finally, since

∂

ur

r

<< 1, the binomial approximation,

12 1 1+≅+ <<aaa,

(D-17)

can be used to find the length of 1' to 2',

′

−

′

=+ ≅+

⎛

⎝

⎜

⎞

⎠

⎟

12 12 1

∂

u

r

dr

u

r

dr

rr

(D-18)

Now recalling the familiar definition of extensional strain as change in length

divided by original length,

ε

∂

r

u

r

dr dr

dr

u

r

=

′

−

′

−−

−

=

+

⎛

⎝

⎜

⎞

⎠

⎟

−

=

1212

12

1

(D-19)

and

ε

r

can now be interpreted as the change in length per original length of a

line segment initially lying along the

direction. In a similar manner, r

ε

θ

can be

shown to represent the change in length per original length of a line segment

initially lying along the

θ

or circumferential direction.

Casing/Tubing Design Manual D-7

October 2005

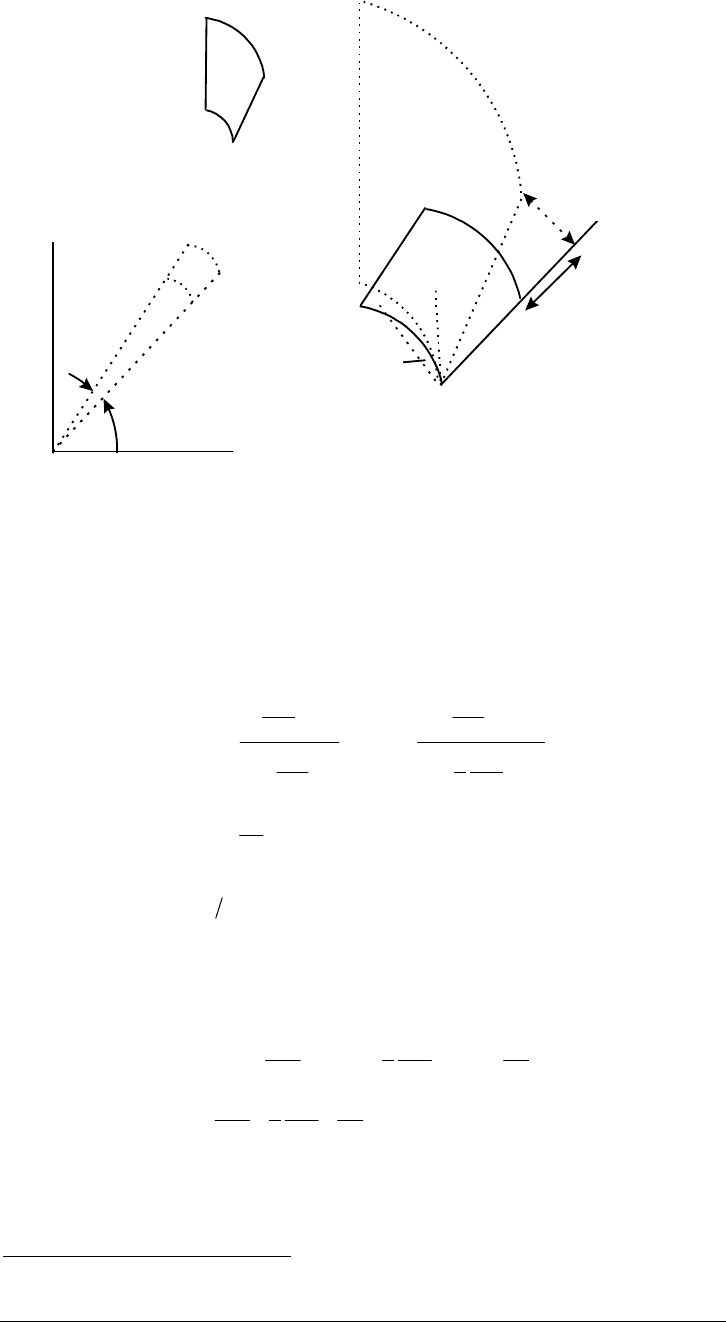
Y

X

r

θ

4

dθ

3

2

1

4

3

2

1,1’

4’

2’

3’

4’

1’

2’

γ

2

γ

1

∂

u

r

/

∂

r dr

∂

u

θ

/

∂

r dr

dr

a. Displacement of 1-2-3-4 b. Rigid body motion removed

Figure D-2. Physical Interpretation of Strain Components

Next, consider the right angle having its vertex at the intersection of arc 1-4 and

line 1-2. After deformation, the change in this right angle is given by

γ

12

+

.

From Figure D-2,

γγ

∂

∂θ

θ

∂

∂θ

θ

12

11

1

+=

+

⎛

⎝

⎜

⎞

⎠

⎟

⎡

⎣

⎢

⎤

⎦

⎥

+

⎛

⎝

⎜

⎞

⎠

⎟

⎡

⎣

⎢

⎤

⎦

⎥

−

⎡

⎣

⎢

⎤

⎦

⎥

−−

−

tan tan

tan

u

r

dr

u

r

dr

u

d

r

u

rd

u

r

(D-20)

where the term

[

tan

−1

ur

θ

]

takes into account the fact that even if u is constant,

the curvature of the differential element will contribute a change in the angles

θ

γ

1

and

γ

2

. Further, since the displacement gradients are small compared to unity,

we can write:

γγ

∂

∂θ

∂

∂θ

θθ

r

u

rr

u

r

u

rr

u

r

+≅

⎡

⎣

⎢

⎤

⎦

⎥

+

⎡

⎣

⎢

⎤

⎦

⎥

−

⎡

⎣

⎢

⎤

⎦

⎥

≅+ −

−−

2

11 1

1

tan tan tan

(D-21)

2

The origin of this term is related to the change in the unit vector

i

in equation (D-6).

~

θ

D-8 Casing/Tubing Design Manual

October 2005

where the last step made use of the small angle approximation, tan

θ

≅ .

Comparing equations (D-21) and (D-10),

(

)

εε

θθ

r

=

r

is seen to be one-half of the

angle change between two perpendicular lines initially lying along the

and r

θ

coordinate directions.

D.3 Stress and Equilibrium

The counterpart to strain, the measure of the deformation experienced by a

material, is stress, the imposed load causing the deformation. Two types of loads

or forces will be considered here: surface forces, or tractions, and body forces.

For these two types of loads, the load intensity can be defined respectively in

terms of the stress vector,

, and the body force vector,

σ

~

χ

~

,

σ

~

lim=

→

∑

F

A

i

∆

∆ 0

(D-22)

χ

~

lim=

→

∑

i

V

∆

∆ 0

(D-23)

In other words, the stress vector,

, is a measure of the local intensity of contact

forces acting on the surface of a body, and is determined by taking the limit of the

resultant contact force,

σ

~

FF

i

~~

=

∑

, acting on a small area

∆

A as the dimensions

of the area become infinitesimal. In a similar vein, the body force vector,

χ

~

, is a

measure of the volumetric intensity of field forces acting on an infinitesimal

volume element

3

.

D.3.1 Decomposition of the Stress Vector

For reasons that will become apparent shortly, it is usually not convenient to work

with the stress vector. Rather, common practice is to decompose the stress into

nine components roughly corresponding to the components of strain (i.e., a

σ

θ

r

stress will result in an

ε

θ

r

strain). In order to formally introduce the components

of stress, consider Figure D-3. The left-hand drawing in Figure D-3 shows a body

B subjected to contact forces such as to place the body in static equilibrium. Only

the surface tractions acting on surface element

∆

A have been shown in order to

avoid cluttering the figure. The right-hand drawing in Figure D-3 is an expanded

view of the area

∆

A and a portion of the body interior to the surface

∆

A. Internal

stress vectors

, , and , acting on the respective coordinate faces, when

combined with the external surface traction,

, render the differential body

σ

~

r

σ

θ

~

σ

~

z

σ

~

3

Although the complexion of the body force vector can be quite involved, the only body

force to be considered here will be that due to the earth's gravitational field.

Casing/Tubing Design Manual D-9

October 2005

element in equilibrium (along with the body force vector

χ

~

not shown). However,

overall vector force equilibrium insists that there also be equilibrium in each of

the three independent coordinate directions. Therefore, it is convenient to

decompose the stress vectors on the coordinate faces,

σ

σσ σ σ

θ

θθ

θ

rr

r

rrz

z

r

z

zr

r

zz

z

iii

ii i

iii

~

~~~

~

~~ ~

~

~~~

,

.

=

+

=++

(D-24)

Using equation (D-24) and noting that

4

:

∆∆

∆

AAnAAnAAn

rr z

=

z

=

,,

θθ

(D-25)

where

n is a unit vector normal to the area

~

∆

A

, the condition that all force

components acting in the

-direction vanish results in: r

−− − ++⋅

⎛

⎝

⎜

⎞

⎠

⎟

=

σσ σ χσ

θθ

rr r zrz r

An An An V i A∆∆∆∆ ∆

1

0

~

(D-26)

with similar expressions holding for the

θ

and -coordinate directions. Factoring

∆

A and noting that the body force enters the expression as a higher order term,

equation (D-26) can be written:

z

σσσ σ

θθ

~

⋅= + +inn

r

rr r zrz

n

(D-27)

where

σ

~

⋅i

r

is the component of the external stress vector . Similar

developments along the remaining coordinate directions lead to:

r

σσ σσ

θ

θθθθ

~

⋅= + +inn

rr zz

n

(D-28)

σσ σ σ

θθ

~

⋅= + +inn

z

rz r z z z

(D-29)

~

4

Consider the area vector . Because the

tetrahedron of Figure D-3 is a closed surface, we must have

, where

∆∆ ∆A An Ani ni ni

r

z

~ ~ ~~~

== ++

⎛

⎝

⎜

⎞

⎠

⎟

θ

∆∆ ∆ ∆AA A A

rz

~~ ~ ~

+++ =

θ

0

∆

AA

r

~~

i

=

−

, etc., which leads immediately to

equation (D-25).

D-10 Casing/Tubing Design Manual

October 2005

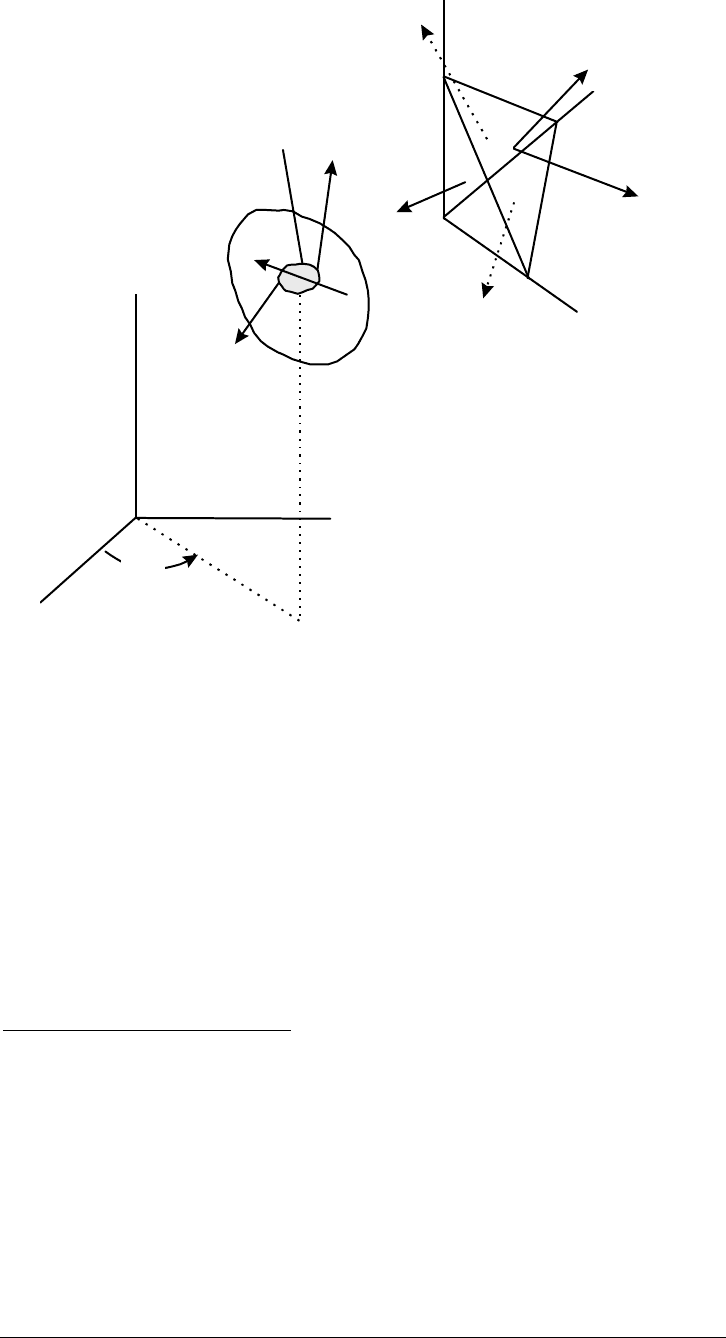
X

Y

r

θ

z

Z

B

F

1

F

2

F

1

σ

z

~

σ

θ

~

σ

r

~

F

3

∆A

θ

∆A

B

σ

~

B

r

z

θ

n

~

σ = F/∆A = (F

1

+ F

2

+ F

3

) / ∆A

~ ~ ~ ~ ~

Figure D-3. Stresses and the Stress Vector

D.3.2 The Equilibrium Equations

Although the introduction of the components of stress is facilitated by considering

a portion of the body adjacent to its surface, the equilibrium equations can be

most easily derived by considering an interior volume element

5

. Examine Figure

D-4 which shows an interior differential element of B whose sides have been

chosen to align with the coordinate directions. According to the normal sign

convention, all of the stress components shown in the figure are positive. For the

body B to be in static equilibrium, each and every differential element in the body

must be in force and moment equilibrium in each of the three coordinate

directions. For example, in the

-direction, force equilibrium is expressed as r

5

A more straightforward derivation of the equilibrium equations can be performed by

noting that for global equilibrium of the body in Figure D-3,

σχ

~

dA dV

AV

∫∫

+=0.

Transforming the area integral to a volume integral by means of the Gauss theorem and

requiring that the resultant integrand on the left-hand side of the equation vanish for all

portions of the body leads directly to the equations of equilibrium (D-34), (D-36) and (D-

37). However, the manipulations associated with application of the Gauss theorem

necessitate the introduction of the gradient operator in cylindrical coordinates, an

unnecessary complication to the scope of this summary. A similar procedure could also

be used to discuss moment equilibrium.

Casing/Tubing Design Manual D-11

October 2005

Casing/Tubing design manual october 2005 Chevron

Подождите немного. Документ загружается.