Cao Z. (Ed.) Thin Film Growth: Physics, materials science and applications

Подождите немного. Документ загружается.

168 Thin ﬁlm growth

(a1) (b1)

(a2) (b2)

(a3) (b3)

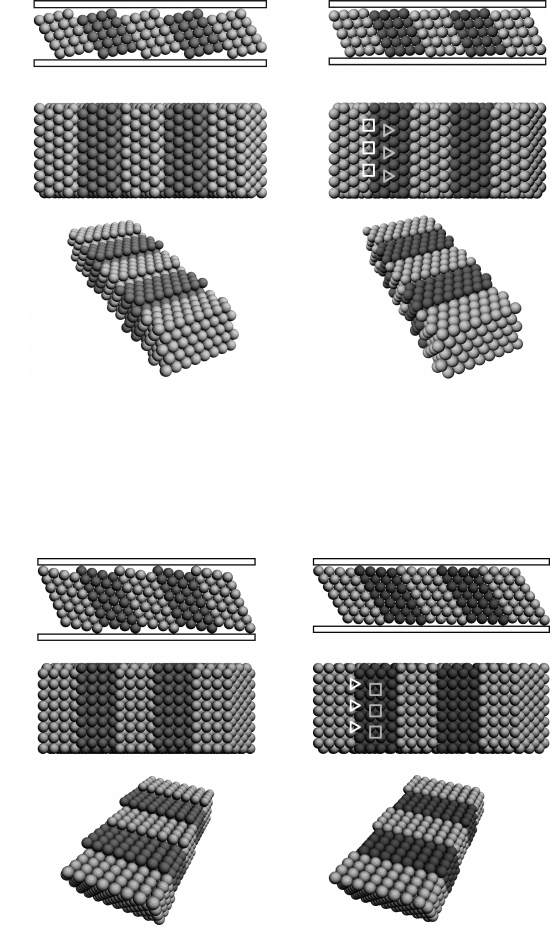
7.13 Models of (b) MVD

and (a) the vicinal FCC(111) they

derive from. Index numbers indicate (1) side view, (2) top view

and (3) perspective view. Different shades of grey show FCC

microcrystallites. Interfaces between microcrystallites in (b) indicate

stacking fault plane position. Grey triangles and white squares

highlight terrace symmetry and square microcrystallite connections

at the terrace interface, respectively.

(a1) (b1)

(a2) (b2)

(a3) (b3)

7.14 Models of (b) MVh and (a) the vicinal FCC(100) they

derive from. Index numbers indicate (1) side view, (2) top view

and (3) perspective view. Different shades of grey show FCC

microcrystallites. Interfaces between microcrystallites in (b)

indicate stacking fault plane position. Grey squares and white

triangles highlight terrace symmetry and triangular microcrystallite

connections at the terrace interface, respectively.

ThinFilm-Zexian-07.indd 168 7/1/11 9:41:45 AM



169Phase transitions in colloidal crystal thin ﬁlms

(mVh

for short). then, stacking faults are periodically distributed as has

been highlighted by the grey to black colour change in Figs 7.12, 7.13 and

7.14. it is important to stress that (111) and (100) facets are not parallel to

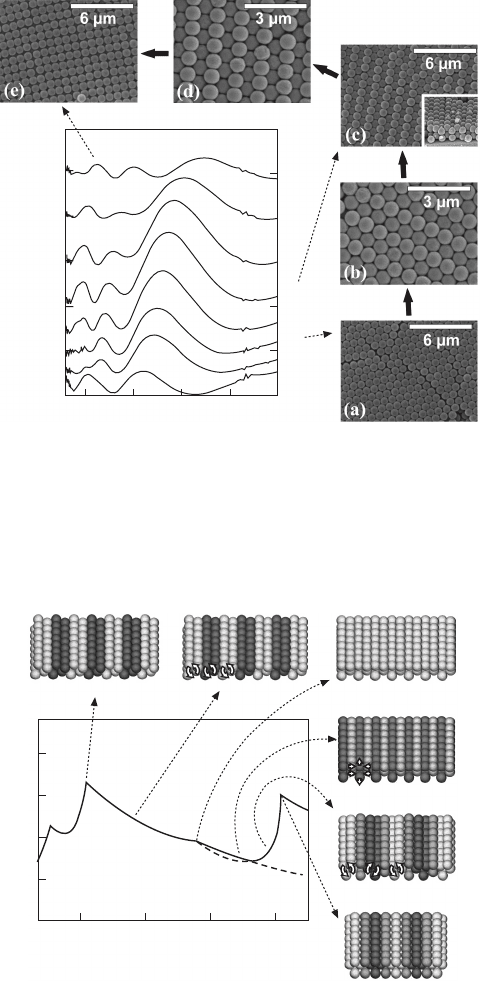
the conning walls, but they are slightly tilted, forming a sawtooth. Figure

7.15 shows sEm images of mVD

(a-b), mVD

by our model.

in the following we show how the mVD

can connect the triangular and

the HCP(100) phases (Ramiro-Manzano et al., 2006b). as the distance

between conning plates increases, the system should maximize the lling

factor value. then, microcrystallites get smaller because more stacking faults

appear and they slightly rotate towards the upright position as shown in

Fig. 7.16. Finally, when the terraces consist of two rows, the stacking fault

planes are perpendicular to the conning plate and the system is formed by

a periodic distribution of stacking faults every two vertical planes. it results

in an ABABAB distribution of layers consistent with a HCP arrangement

(see Fig. 7.16(d)). Figure 7.17 shows the SEM image of the HCP(100)

arrangement predicted by our model. the free surface of this phase looks like

a set of parallel strings of particles (Fig. 7.16(d)) whose distance between

(a)

(c)

(b)

(d)

5 µm

9 µm 4 µm

4 µm

7.15 SEM images of MVD

(a) top view (b) cleft edge; MVD

view and MVh (d) top view. Black and white colour triangle and

square symbols highlight terrace symmetry and microcrystallite

connections, respectively. Image (b) is taken from Ramiro-Manzano

et al. (2006b) with permission of the Americal Physical Society (APS).

ThinFilm-Zexian-07.indd 169 7/1/11 9:41:45 AM



170 Thin ﬁ lm growth

them, d, is d =

(

)

. optical spectra can give additional information

about colloidal order that can be complementary to that obtained with sEm

analysis. Figure 7.18 shows HCP(100) experimental spectrum (continuous

line) and the theoretical calculation (dotted line) of nine monolayers with

HCP symmetry oriented along the (100) direction (9 HCP(100) for short), 770

(a)

(b)

(c)

(d)

7.16 Model of the transition D (a) Æ MVD

(b-c) Æ HCP(100) (d).

White and grey colour triangles highlight terrace symmetry and

microcrystallite connections, respectively.

5 µm

7.17 SEM image of 4HCP(100). From Ramiro-Manzano et al. (2007)

with permission of the Americal Physical Society (APS).

ThinFilm-Zexian-07.indd 170 7/1/11 9:41:46 AM



171Phase transitions in colloidal crystal thin ﬁlms

nm being the particle size. We have swept the light spot of the spectrometer

through different regions of the colloidal crystal. Figure 7.19 shows the optical

spectra of three different phases. the spectrum of nine monolayers of the

mVD

phase (9 mVD

) shows a Bragg peak located at a wavelength value

between the peak positions of the 9D and the 9HCP(100). As a consequence

the mVD

phase can be considered as an intermediate phase between the D

and the HCP(100) particle orderings.

the mVh and mVD

arrangements can explain the transition between the

FCC (100) (Fig. 7.20(a)) and the FCC(111) (Fig. 7.20(h)) through the phase

HCP(011) (Fig. 7.20(d) and (e). This transition sequence is very similar to

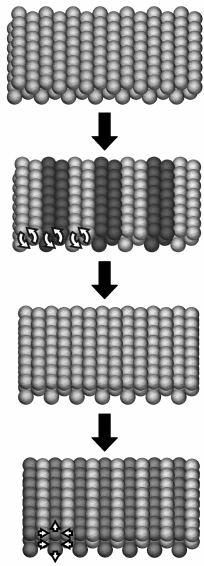
that shown in Fig. 7.16. Figure 7.20(a) shows the model of a 5h colloidal thin

Reﬂectance (a.u.)

0.8

0.6

0.4

0.2

0.0

2.5 2.0 1.5 1.0

l (µm)

Reﬂectance (a.u.)

0.5

0.4

0.3

0.2

0.1

0.0

2.5 2.0 1.5

l (µm)

7.18 Experimental spectrum (continuous line) and theoretical

calculation (dotted line) of the 9HCP(100) phase.

7.19 Optical spectra of 9D (dotted line), 9MVD

(continuous line) and 9

HCP(100) (dashed line).

ThinFilm-Zexian-07.indd 171 7/1/11 9:41:46 AM



172 Thin ﬁlm growth

lm. When a periodic distribution of stacking faults is introduced it results

in a colloidal arrangement like the model in Fig. 7.20(b), that corresponds

to a vicinal facet mVh with a periodic distribution of squared arranged

micro-crystallites, four rows large, with triangular arranged strips in the

joints between them. Figure 7.20(c) and (d) are similar to Fig. 7.20(b) but

here the stacking distribution appears each three and two rows, respectively.

the latter corresponds to a periodic distribution of particle strings where

triangular and square orderings alternate (right panel of Fig. 7.20(d)). in fact,

it corresponds to ABABAB (Fig. 7.20(d)) consistent with the HCP lattice

oriented along the (011) direction (HCP(011) for short). Therefore, the

HCP(011) could be considered as the stack (AB)(AB)(AB) of square facet

microcrystallites (see shades of grey in Fig. 7.20(d)). this type of particle

arrangement can be seen in the sEm images in Fig. 7.21.

the process of introducing periodic distribution of stacking faults can

continue evolving the system from the HCP(011) phase to the D one. From the

model of Fig. 7.20(d) one can select the appropriate slipping plane resulting

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

7.20 Model of the transition nh (a) Æ nMVh (b–c) Æ nHCP(011) (d–e)

Æ nMVD

(f–g) Æ D (h). White and grey colour symbols highlight

terrace symmetry and microcrystallite connections, respectively.

ThinFilm-Zexian-07.indd 172 7/1/11 9:41:46 AM



173Phase transitions in colloidal crystal thin ﬁlms

in Fig. 7.20(e) that corresponds to the mV composed by triangular terraces

joined by square steps (mVD

). the triangular facet growth leads the stacking

faults to continue the rotation towards the upright position increasing the

whole thickness (Fig. 7.20(f)–(g)). Finally, the process ends and the terrace

lls all the space (the distance between stacking faults is innite) creating

the triangular facet (Fig. 7.20(h)). the mV phase can be considered as a

group of particle ordering including the HCP for a two-row terrace case

and the FCC facet for the case of innite length terrace. Consequently, the

mV phase opens a new phase sequence scenario connecting the following

particle orderings:

nh Æ nmVh

Æ nHCP(011) Æ nmVD

Æ nD

Æ nmVD

Æ nHCP(100) [7.3]

When this transition takes place by mV composed of only two-row terrace

size (that is HCP), the slipping plane evolution is clearly observable since

it covers long areas. For this reason we will include this long transition in

the ordering sequence as a new phase, the HCP-like.

The HCP-like and the pre-h phases

The HCP-like (100) phase (HCPL for short) covers large regions of the

sample because it adapts itself to the progressive changes of the cell thickness

4 µm 4 µm

(a) (b)

7.21 SEM images of HCP(011) (a) top view and (b) cleft edge. White

colour squares and triangles highlight the surface symmetry. From

Ramiro-Manzano et al. (2009) with permission of the Royal Society of

Chemistry (RSC).

ThinFilm-Zexian-07.indd 173 7/1/11 9:41:47 AM



174 Thin ﬁ lm growth

by a smooth change in the interlayer spacing. moreover, we also show

the buckling phase as a particular case of the HCPL ordering. Finally, we

show a very unstable colloidal arrangement, the pre-h phase, to explain the

transition nDÆ (n + 1)h.

The HCPL phase can be considered as a generalization of the HCP(100)

particle arrangement where the distance between linear strings of spheres is

well determined. However, this distance takes different values for the case

of the HCPL phase. Figure 7.22 shows SEM images of different particle

arrangements corresponding to (a) HCPL with a distance d ≈ 1.68 F, (b)

HCP(100) with a well-known distance d =

(

)

arrangements corresponding to (a) HCPL with a distance

= 1.63F and (c) HCPL

with a distance d ≈ 1.52F. The HCPL phase has been observed in many

ordering transitions nD Æ (n + 1)h. Here we discuss the transition 2D Æ

3h. This will help us to understand better the HCPL phase, and also it would

allow us to introduce the pre-3h phase. the analysis of their corresponding

optical spectra, and the comparison to the sEm images (see Fig. 7.23), allows

us to make an accurate assignment of the particle arrangement. optical

features in the re ectance also show gradual changes. Firstly, as the system

transits between 2 and 3 monolayers a new oscillation period gradually

appears. secondly, the Bragg diffraction peak absent in the 2h facet, clearly

emerges in the 2D arrangement (at l = 1.7 µm). Then, for the 2HCPL phase,

it shifts at longer wavelength values and smoothly fades out (at around l =

2.2 mm) when the light spot approaches the 3h ordering. Recently, schöpe

et al. (2006) have described two and three buckling phases in wet colloidal

crystal thin  lms, that in fact correspond to HCPL phase we are describing

here.

Figure 7.24 shows the calculated  lling fraction in the 2Δ Æ 3h transition.

Here we show how the different facets evolve as the cell gap increases.

(a) (b) (c)

2 µm 2 µm 2 µm

7.22 SEM images of different particle arrangements (a) HCPL d ª

1.68F, (b) HCP(100) d =

)

F = 1.63F and (c) HCPL d ª 1.52F,

d being the distance between linear strings of spheres and F the

sphere diameter. From Ramiro-Manzano et al. (2007) with permission

of the Americal Physical Society (APS).

ThinFilm-Zexian-07.indd 174 7/1/11 9:41:47 AM



175Phase transitions in colloidal crystal thin ﬁlms

2HCP

1.0 1.5 2.0 2.5 3.0

l (µm)

Reﬂectance (arb. units)

0.6

0.5

0.4

0.3

0.2

0.1

0.0

7.23 Reﬂectance optical spectra obtained over a path in the sample

for the transition between 2D and 3h, being the sphere diameter 770

nm. SEM images of the sequence of the different facets: (a) 2D, (b,d)

2HCPL, (c) HCP(100), and (d) 3h. The inset in (c) shows a cleft edge.

From Ramiro-Manzano et al. (2007) with permission of the Americal

Physical Society (APS).

2 HCPL 2 HCP(100)

2 HCPL

pre-3h

(a) (b) (c)

(d)

(e)

(f)

1.8 2.0 2.2 2.4

h/F

ff (%)

7.24 Filling fraction calculation between 2D and 3h as a function

of the reduced cell thickness h/F, F being the particle diameter.

From Ramiro-Manzano et al. (2007) with permission of the Americal

Physical Society (APS).

ThinFilm-Zexian-07.indd 175 7/1/11 9:41:48 AM



176 Thin ﬁlm growth

the local maximum at h/F = 1.82 corresponds to the 2Δ phase. As the

cell becomes thicker the system smoothly transits to the 2HCPL phase.

The groups of microcrystallites articially selected with different shades

of grey can help in understanding the transitions between different particle

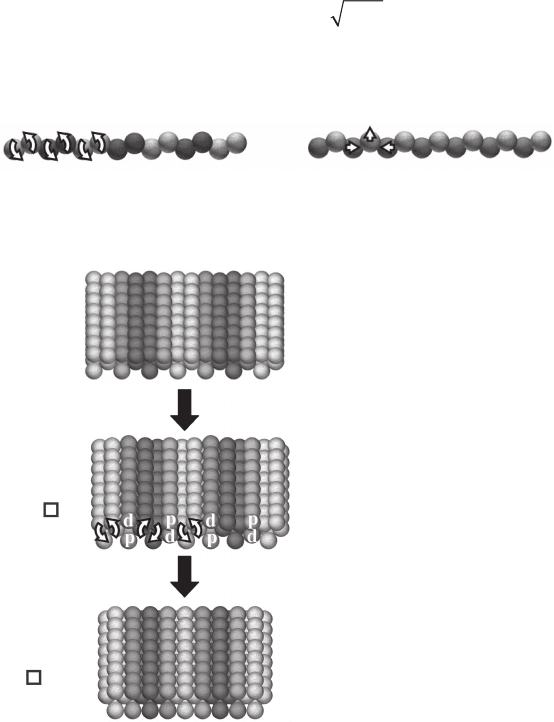
arrangements. The 2Δ Æ 2HCPL(100) Æ 2HCP(100) transition takes place

when all microcrystallites, as mention before, rotate around their longer

axis (the [110] direction), thus forming, rst, the 2HCPL phase (packing

model (b) in Fig. 7.25) and then, the 2HCP(100) phase (packing model (c)

in Fig. 7.25). As the lling fraction value also decreases monotonically, the

2HCPL is very stable, and, as expected, it can be found in large regions

of the sample. an animated movie of the ordering evolution is shown in

Ramiro-manzano et al. (2007). The transition 2HCP(100) Æ 3h continues

through another 2HCPL phase (packing model (d) in Fig. 7.25). As the cell

thickness increases, the upper (lowest) sublayer displaces itself vertically

upwards (downwards) and the rows come closer together. simultaneously,

in order to maximize lling fraction, the rows from the second and the third

(a)

(b)

HCPL(100)

(c)

HCP(100)

(d)

HCPL(100)

7.25 Model of the transition 2D (a) Æ 2HCPL(100) (b) Æ 2HCP(100)

(b) and sphere string movements in (d).

ThinFilm-Zexian-07.indd 176 7/1/11 9:41:48 AM



177Phase transitions in colloidal crystal thin ﬁ lms

sublayer approach each other to form the 2HCPL phase. Therefore, packing

models (b–d) in Fig. 7.25 correspond to sEm images (b–d) in Fig. 7.22.

The HCPL(100) phase has strong resemblances to the buckling arrangement

(Pansu et al., 1984). the buckling phase can be imagined as alternate single

string rows that evolve for adapting to the gap cell of the con ning plates. Figure

7.26 shows equivalent models of the evolution of the string rows adapting to

the increasing cell thickness value. in Fig. 7.26(a) the groups composed of two

sphere strings rotate to adapt themselves to the increasing values of the cell

gap. However, in Fig. 7.26(b) the lower sublattice of parallel particle strings

approach each other and the upper sublattice shifts upwards. Both models

can account for the change in the particle ordering. the models of Fig. 7.26

also appear in the HCP(100) phase. In fact when the distance between the

upper and lower rows of Fig. 7.26 is exactly

(

)

, the buckling phase

can be considered as a monolayer of the HCP(100) ordering.

Figure 7.24 shows a new phase, the pre-3h phase not discussed yet. this

phase is a transitory ordering connecting 2HCP(100) and the 3h. Figure 7.27

(a) (b)

7.26 The buckling phase as 1HCPL. Arrows in (a) and (b) show the

HCPL transition mechanisms.

(a)

HCP(100)

(b)

Pre-3

(c)

7.27 Model of the transition (a) 2HCP (100) Æ (b) pre-3h Æ (c) 3h.

White arrows show microcrystallite rotations.

ThinFilm-Zexian-07.indd 177 7/1/11 9:41:48 AM

