Cao Z. (Ed.) Thin Film Growth: Physics, materials science and applications

Подождите немного. Документ загружается.

128 Thin ﬁlm growth

solution for 240 seconds at room temperature. The sample was then rinsed

and dried. The top-view SeM images of the patterned area with 100 nm

pillars and 50 nm pillars are shown in Fig. 6.2(c) and (d), respectively. The

patterned surfaces fabricated by lithography can be used as a ‘hard mold’

for nanoimprint lithography for massive production of cost-efcient seeds.

Malac et al. (1997) used e-beam lithography to prepare the patterned surfaces

for oblique angle deposition. They chose poly-(methylmethacrylate) (PMMA)

as the resist. After the resist is patterned, a lift-off step is followed to form

pillars as the PMMA is a positive tone e-beam resist. Horn et al. (2004a)

used a negative resist in e-beam lithography, therefore no lift-off process is

involved. In addition to the seeds mentioned above, self-assembled seeds

and patterned surfaces with lines or holes were used to grow nanostructures

by oblique angle deposition (Zhao et al., 2002a; Horn et al., 2004b).

The geometry of the seeds has a signicant effect on the morphology of

(a)

(c)

(b)

(d)

rpi SEI 5.0kV X10.000 1µm WD 11.2mm

rpi SEI 5.0kV X10.000 1µm WD 11.1mm

1 µm

EHT = 5.00 kV

WD = 10 mm

Mag = 30.20 KX

Singal A = InLens

Date:12Sep 2007

Time:21:57:41

ZEISS

1 µm

EHT = 5.00 kV

WD = 10 mm

Mag = 30.20 KX

Singal A = InLens

Date:12Sep 2007

Time:22:01:21

ZEISS

6.2 SEM top-view images of templated surfaces prepared for oblique

angle deposition. (a) W pillars after removing the SiO

matrix. The

seeds were arranged in a square lattice with a 1000 nm lattice

constant. (b) W pillars were arranged in a triangular lattice with a

750 nm lattice constant. (c) Arrays of 100 nm hydrogensilsesquioxane

(HSQ) pillars in a square lattice with a 750 nm lattice constant

fabricated by e-beam lithography. (d) Arrays of 50 nm HSQ pillars in

a square lattice by e-beam lithography.

ThinFilm-Zexian-06.indd 128 7/1/11 9:41:15 AM



129Silicon nanostructured ﬁ lms grown on templated surfaces

the nanostructures grown on them in oblique angle deposition, particularly the

size of individual seeds. Obviously, the size of the seeds should be suf ciently

small in order to deposit a single nanostructure on each seed. We deposited

Si on W seeds with a diameter of 360 nm and observed multiple nanorods

grown on top of the seeds, while single nanorods can be grown on smaller

W seeds with a diameter of 150 nm, all under the oblique angle deposition

conditions with an 85∞ incident angle and uniform substrate rotation (Ye

et al., 2008). In oblique angle deposition on templated surfaces, the shadowing

effect from the nearest seed is dominant, no matter whether or not the substrate

is rotated (Ye et al., 2008). We call the shadowing effect from the nearby

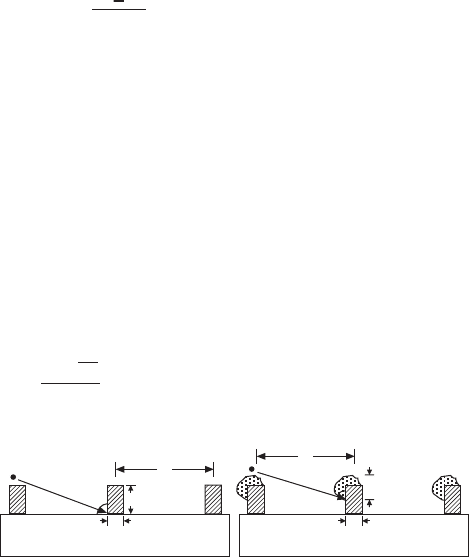
features on the surface as ‘global shadowing effect’. We can determine a

cut-off angle of the incident  ux q

in terms of the seed geometry, namely,

the size of the seeds D, the height of the seeds H, and the center to center

separation of the nearest seeds L, as depicted in Fig. 6.3 (a). The equation

can be written as

–1

()

LD – LD

()

LD – LD

[6.4]

which is similar to the arguments by Hawkeye and Brett (2007), and Horn et

al. (2004a,b). If the incident angle q > q

, the global shadowing can affect the

growth of nanostructures on each seed at the very beginning of the oblique

angle deposition. In practice, the incident angle q is much larger than q

Therefore, we de ne another important geometric factor, ‘exposure height’

a, in oblique angle deposition on seeds. The exposure height determines the

uniformity and morphology of the nanostructures (Ye et al., 2008). It can be

de ned as the portion of an individual seed or nanostructure exposed to the

deposition  ux incorporating the shadowing from the nearest neighbors in

the plane of deposition  ux and the axis of seeds, as sketched in Fig. 6.3(b).

Hence, the exposure height a can be represented as

–

[6.5]

(a) (b)

6.3 Schematic of the geometry of the seeds. (a) The cut-off angle

is the minimum incident angle of the ﬂ ux that allows global

shadowing effect. (b) The exposure height a of the growing

nanostructures at a ﬁ xed incident angle q.

ThinFilm-Zexian-06.indd 129 7/1/11 9:41:16 AM



130 Thin ﬁlm growth

From the denition, the growing portion of the nanostructure within a should

not be affected by the global shadowing from its neighbors. We suspected

that the growth of the surface in this part may be controlled by the same

mechanisms as that of surface growth on a seed with normal incident ux,

i.e. by surface diffusion, ballistic sticking, self-shadowing, etc.

6.3 Fan-out on templated surface with normal

incident ﬂux

6.3.1 Experimental observation of fan-out growth on

templated surface

We discussed the shadowing effect and developed a geometrical model to

describe the shadowing effect in oblique angle deposition in the previous section

in this chapter. Now we move on to the discussion of growth mechanisms

with normal incident ux in experiments and Monte Carlo simulations. In

this section, we reported the creation of a fan-like structure by a simple line-

of-sight evaporation technique where atoms vertically drop down onto an

array of nano-sized cylindrical W seeds. Very well dened fanlike clusters

are formed on these seeds. The morphology of fan-like structures will be

shown and analyzed from the SeM images. A ballistic deposition model will

be developed to interpret the growth mechanisms of the structures.

The templated surfaces containing W pillars in a square lattice were used

for the silicon (Si) depositions with normal incident ux in our experiments.

The substrates were placed at a position such that their normal vectors

pointed to the source. Thus, the incident angle of the ux q is equal to 0∞

measured from this surface normal vector. The angular dispersion of the ux

is less than 0∞ due to the geometry of our deposition system, i.e. the distance

between the source and the substrate is about 35 cm and the diameter of

the mouth of the crucible is 1 cm. Therefore, the ux can be assumed as a

parallel ux in our experiment. Before the deposition, the area containing W

pillars on the substrate was centered to the incident ux using a laser beam

that simulates the incoming ux.

Si (99.9999%, Alfa Aesar) was evaporated from a graphite crucible by

electron-beam bombardment as described elsewhere (Wong et al., 1987;

Mei and Lu, 1988). The evaporation rate was measured by a quatz-crystal

microbalance (QCM, Maxtek TM-350/400) and maintained at 5.0 ± 0.3 Å/s

during the deposition by adjusting the power levels supplied to the crucible.

Two sets of samples were prepared with normal thickness of 700 nm and 800

nm as measured by the QCM. To study the morphology of the samples, SEM

images were taken using a eld-emission SEM. The samples were coated by

a ~10 nm thick Pt lm to reduce the charging effect before loading into the

SeM system. A very sharp tungsten tip was heated to release electrons in

ThinFilm-Zexian-06.indd 130 7/1/11 9:41:16 AM



131Silicon nanostructured ﬁlms grown on templated surfaces

the SeM. The emission current ranges from 6.5 to 12.5 mA during operation.

For the SEM cross-sectional views, the samples were cleaved in a direction

along the axis of the square lattice. SEM top view images were also taken.

The SeM images were used for further analysis using Photoshop (Adobe,

Version 6.0), an image processing software.

We observed experimentally that the growth of Si on a templated substrate

with a regular array of W pillars would give rise to a phenomenon referred to

as ‘fan-out’ growth in normal deposition without substrate rotation (Ye and

Lu, 2007a). Figures 6.4 and 6.5 demonstrate this phenomenon by the SEM

top-view images and cross-sectional images of 700 nm and 800 nm thick Si

lms deposited on the W pillars arranged in a square lattice. Well-dened

3D fan-like structures were observed on top of each seed. If the deposition

time is long enough, the nanostructures grown on the seeds will touch their

neighbors, as we can see from the top-view image of those structures on

the large seeds in Fig. 6.5(a). A structure with a pyramidal shape was also

(a)

(c)

(b)

(d)

360nm

150nm

RPI SEI 5.0kV X15.000 1µm WD 10.8mm

RPI SEI 5.0kV X15.000 1µm WD 10.7mm

RPI SEI 5.0kV X30.000 100nm WD 11.1mm

RPI SEI 5.0kV X30.000 100nm WD 10.2mm

6.4 SEM images of ballistic fan-like Si structures grown on a square

lattice. The thickness of the Si ﬁlm is 700 nm. (a) and (b) are the top-

view image and the cross-sectional image of the structures on large

W pillars with a 360 nm diameter, respectively. (c) and (d) are the

SEM images of similar structures on small W pillars with a 150 nm

diameter.

ThinFilm-Zexian-06.indd 131 7/1/11 9:41:16 AM



132 Thin ﬁlm growth

deposited inside the open area on the substrate between the seeds. One can

see that the outlines on the side of the fans are straight and can be described

geometrically by three-dimensional solid cones. Therefore, the width of the

fan-like cones grew linearly with time.

6.3.2 Monte Carlo simulation of ballistic fans

There has been much study of the theory on the formation (Ramanlal and

Sander, 1985; Limaye and Amritkar, 1986) of this fan-like structure as

well as the scaling properties (Liang and Kadanoff, 1985; Porcu and Prodi,

1991; Krug and Meakin, 1991) of the fan based on the ballistic aggregation

(a)

(c)

(b)

(d)

360nm

150nm

RPI SEI 5.0kV X15.000 1µm WD 11.5mm

RPI SEI 5.0kV X15.000 1µm WD 12.0mm

RPI SEI 5.0kV X30.000 100nm WD 10.4mm

RPI SEI 5.0kV X30.000 100nm WD 11.1mm

6.5 SEM images of ballistic fan-like Si structures grown on a square

lattice. The thickness of the Si ﬁlm is 800 nm. (a) and (b) are the

top-view image and the cross-sectional image of the structures on

large W pillars with a 360 nm diameter, respectively. The ballistic

fans contact their neighbors and are connected as seen in (a). (c) and

(d) are the SEM images of similar structures on small W pillars with

a 150 nm diameter. (Adapted from Ye and Lu, 2007a, reprinted with

permission.)

ThinFilm-Zexian-06.indd 132 7/1/11 9:41:17 AM



133Silicon nanostructured ﬁlms grown on templated surfaces

mechanism. Although most of the studies are in two dimensions, an extension

to three-dimension simulation has also been reported (Kardar et al., 1989).

However, thus far very scarce experimental demonstration has been reported

on the formation of this fan-like structure. In our study, a Monte Carlo (MC)

simulation with nearest-neighbor ballistic sticking followed by a diffusion

mechanism has been proposed to describe the fan-like structures.

Very few theoretical studies of the surface evolution concerning patterned

surfaces have been carried out, mainly due to the crossover of the scales

in this system. Typically, the size of individual patterns varies from tens

of nanometers to several hundreds of nanometers. each of these patterns

is a result of the deposition where the atomic level surface processes and

the mesoscopic processes such as mass transport cooperate to determine

the growth of nanostructures on top of it. Based on this fact, the model we

choose to simulate the surface growth at this scale should be able to handle

the following processes (Imry, 2002):

∑ generating non-smooth patterned surfaces;

∑ multi-valued surface proles;

∑ incorporation of atomic level surface processes, such as diffusion;

∑ complex stochastic processes in mesoscopic scales.

Ideally, multi-scale simulation techniques can provide the best solution in

this situation (Castez and Salvarezza, 2006). However, in the context of

limited resources, MC simulation can also address some of the issues listed

above. In general, physical events including deposition of particles at random

positions, surface diffusion, surface hopping, and evaporation of surface

particles, can be embedded into the MC simulation.

Most recently, the importance of mass transport has been evaluated in

surface growth models (Suzuki and Taga, 2001; Raible et al., 2002; van

Dijken et al., 1999; Luedtke and Landman, 1989). This mass transport can be

due to the inter-atomic interaction of the incoming particles and the surface

particles (referred to as the ‘steering effect’), and geometric effects such

as the shadowing effect. The steering effect and other growth mechanisms

will be studied by 3D MC simulations. In our MC model, a 3D lattice with

dimensions 1024 ¥ 1024 ¥ 1024 is formed by cubic lattice points. One cube

represents an incident particle so that it has the dimension of a cubic lattice

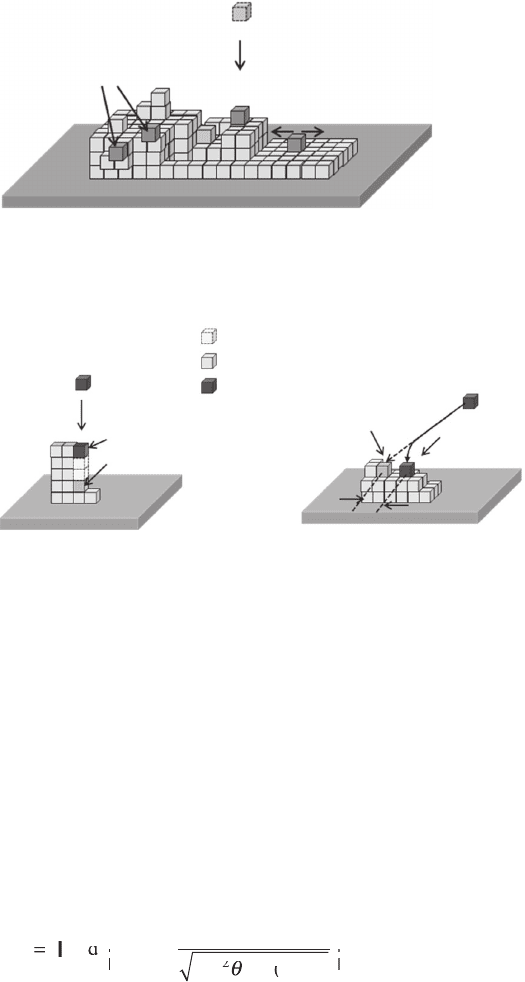
point. Figure 6.6 shows a schematic of the simple cubic system in this MC

simulation with ballistic sticking and surface diffusion processes allowed.

In the ballistic sticking model, an incident atom moving into an empty

nearest-neighbor lattice point will occupy that empty position immediately.

In contrast, in a solid-on-solid model, that atom will pass that empty spot

unless it is the lowest position the atom can go in the system (Amar and

Family, 1990). We believe that the ballistic sticking model of incident atoms

comes from the inter-atomic interactions.

ThinFilm-Zexian-06.indd 133 7/1/11 9:41:17 AM



134 Thin ﬁ lm growth

The interaction of atoms is due to the Lennard–Jones (L-J) potential,

which is widely used, in the form of

U(r) = 4e[(s/r)

– (s/r)

], [6.6]

where the parameters e and s depend on the properties of the atom. Using

the equation developed by Raible et al. (2002), we can estimate the variation

of the distance ∆x from the impact point of a linear trajectory as in Fig.

6.7(b). The distance can be calculated from Raible et al. (2002) using the

L-J potential for Si,

xz =xz

xz dxz

–

•

xz dxz

vzs(vz

– s( –

[6.7]

For our oblique angle deposition setup, the incident angle of the particles

is close to 90∞, thus we can ignore the cosine part inside the square root in

Incident atom

Deposition

Ballistic sticking

Diffusion

6.6 Schematic of 3D Monte Carlo simulation with ballistic sticking

and surface diffusion processes on a smooth substrate. The ﬂ ux of

atoms approaches the surface from the top along the surface normal.

Ballistic sticking

Empty space

Occupied sapce

Depositing atom

Solid-on-solid

Ballistic sticking

Solid-on-solid

(a) (b)

6.7 Ballistic sticking model in the MC simulations with (a) top-down

and (b) oblique angle incident ﬂ ux. The possible deposit sites of the

incident atoms due to the ballistic sticking model and the solid-on-

solid model are labeled for comparison.

ThinFilm-Zexian-06.indd 134 7/1/11 9:41:17 AM



135Silicon nanostructured ﬁlms grown on templated surfaces

Eq. 6.7. If the kinetic energy E

of the incident particle is about 0.3 eV, the

integral of this equation from 0.5 to 0.55 nm yields ∆x ≈ 0.455 nm. That

means the particle was trapped by the surface already by the L-J potential

in the form of Eq. 6.6. The approximated calculation shows that the particle

will be pulled down from its trajectory when passing by an atom. This

means that ballistic sticking is a good approximation in Si with very low

kinetic energy.

3D MC simulations with and without ballistic sticking were performed in

a cubic box with dimension N ¥ N ¥ N (N = 1024). The substrate containing

seeds in a square lattice is xed. The particles were injected into the system

from the top and moved downward. When the particle passes by any deposited

particle in its nearest-neighbor vicinity, it will stick to that particle and

become its nearest neighbor (ballistic sticking model). In order to study the

mechanisms of fan-out growth, we will compare the simulation results with

and without ballistic sticking mechanisms. In our deposition system, the ux

is very uniform due to the large distance between the opening of the crucible

and the substrate. The opening of the crucible is 1 cm, and the distance is

about 35 cm. So, the angle spanned by this geometry is determined to be

less than 2∞. In our simulations, this angular spreading of ux is taken into

account as well.

In the 3D MC simulations, arrays of lattice points are selected and

occupied by particles to represent the W pillars on the templated surfaces.

The cylindrical seeds are placed on a smooth surface on the bottom of the

simulation box with a dimension of 1024 ¥ 1024 units and a thickness of

8 units. The seeds have a diameter of 24 units or 36 units for the small

size seeds or the large size seeds, respectively. The seeds are arranged in

a square lattice with a lattice constant of 256 units. The particular reason

for this arrangement is to avoid overlapping on the boundary by enforcing

periodic boundary conditions. This means that if a particle moves outside

of the cubic system, it will re-enter from the opposite side. The height of

the seeds is 80 units. Figures 6.8 (a) and (b) show the top-view and cross-

sectional images of the smaller seeds, respectively. Similar images of the

large size seeds are shown in Figs 6.8(c) and (d).

First, we investigated the deposition of particles without ballistic sticking,

namely, the particles approaching the surface until they are stopped by

another particle deposited on the surface. When a particle is landed on the

surface, a certain number K of particles, referred to as ‘diffusers’, within

a cubic box with a side of 2a + 1 (a = 5) around the deposited particle

are randomly selected to diffuse on the surface (Kessler et al., 1992). The

number K is related to the diffusivity of material. We used the coordination

numbers as the criteria of the successful diffusion. That means the diffuser

will move to the new lattice point if that move increases the coordination

numbers. Otherwise, it will remain at the same lattice point. The coordination

ThinFilm-Zexian-06.indd 135 7/1/11 9:41:17 AM



136 Thin ﬁ lm growth

numbers include the number of the nearest neighbors (NN) and the number

of next-nearest neighbors (NNN) of the diffuser. Diffusion models that use

NN and NNN numbers have also been adapted by other researchers (Suzuki

and Taga, 2001; Stasevich et al., 2004; Johnson et al., 1994; Smilauer et al.,

1993). However, our diffusion model does not include the kinetic mechanism

associated with the bonding energy, which is different from the models used

in molecular beam epitaxial growth (Stasevich et al., 2004; Johnson et al.,

1994; Smilauer et al., 1993). The model used by Suzuki and Taga is the

closest one to our model, which also deals with oblique angle deposition

(Suzuki and Taga, 2001). In their approach, the site is selected from a cubic

box with 3 units centered at the diffuser. The site with more coordination

numbers will have a greater chance of the diffuser jumping into it according

to the probability of diffusing from site A to site B:

)

ABÆAB

exp(

)

[6.8]

where l is a constant and the summation is taken over all of the allowed sites

(a)

(c)

(b)

(d)

Substrate

Seeds

Small seeds

Big seeds

6.8 Templated surfaces containing seeds in a square lattice in the MC

simulations: (a) top-view and (b) cross-sectional images of the small

seeds 8 units in diameter. (c) and (d) are the top-view and the cross-

sectional images of the big seeds with a diameter of 18 units. The

height of the seeds is 80 units and the lattice constant of the square

lattice is 256 units. The sizes of the images are 1024¥1024 units.

ThinFilm-Zexian-06.indd 136 7/1/11 9:41:17 AM



137Silicon nanostructured ﬁlms grown on templated surfaces

(Suzuki and Taga, 2001). After the diffuser makes a jump, it will continue

the diffusion process to about 10 steps of jumping. It is not clear how the

coordination numbers have been counted in the simulation model by Smy et

al. (2000) for oblique angle deposition. From the precursor of their model,

we know the diffusion model not only counts the coordination numbers but

also the distance between the two sites. And the diffuser can jump over a

long distance without staying on the surface (Dew et al., 1992). Thus, the

diffuser is more likely to jump into a saddle point on the surface in the

model by Smy et al. (Smy et al., 2000). Figure 6.9 shows the top-view and

cross-sectional images of the structured lms generated by the simulations

on two types of seeds without ballistic sticking. The particles were deposited

on the top area of individual seeds, as well as the substrate area between the

seeds. A vertical rod-like structure is formed with uniform size. A continuous

lm was deposited in the gap between seeds as well. The number K in this

simulation was 100, representing the diffusivity of the material. We tried other

K numbers in simulations but we found that the results have no signicant

difference from those shown in Fig. 6.9. However, the simulated results as

shown in Fig. 6.9 are different from the experimental results depicted in

Fig. 6.4. That means the deposition model without ballistic sticking cannot

be used to explain the fan-out growth phenomenon.

6.3.3 Growth exponent of ballistic fans

The 3D MC simulations with the ballistic sticking model have been carried out

on the same pre-occupied seed arrays. The particles drop down randomly and

(a) (b)

6.9 Monte Carlo simulations of particles deposited on (a) small seeds

and (b) big seeds in the solid-on-solid model with diffusion. The

diffusion number K is 100.

ThinFilm-Zexian-06.indd 137 7/1/11 9:41:17 AM

