Cain G., Meyer G.H. Separation of Variables for Partial Differential Equations: An Eigenfunction Approach

Подождите немного. Документ загружается.

page_172

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_172.html[22/02/2009 23:53:14]

< previous page page_172 next page >

Page 172

(

=wt(L, t)

=0.

The associated eigenvalue problem is again

The eigenfunctions are

The approximating problem is

where

The approximating problem has the solution

where

αn(t)

has to satisfy the initial value problem

It is straightforward to integrate this equation numerically. Moreover, as the following discussion shows,

its solution for

>0 is a decaying oscillatory function of time and hence can be computed quite

accurately. A numerical integration would become necessary if the resisting forces in this model are

nonlinear. Such forces would generally lead to a coupling of the initial value problems for

{αn(t)},

but

such nonlinear systems are solved routinely with explicit numerical methods.

It also is straightforward, and useful for analysis, to solve the equation analytically. Its solution has the

form

αn(t)=C1nαn1(t)

C2nαn2(t)

αnp(t)

< previous page page_172 next page >

page_173

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_173.html[22/02/2009 23:53:15]

< previous page page_173 next page >

Page 173

where

αn1(t)

and

αn2(t)

are complementary solutions of the homogeneous equation and

αnp(t)

is any

particular integral. For the complementary functions we try to fit an exponential function of the form

αc(t)=ert.

Substitution into the differential equation shows that

must be chosen such that

This quadratic has the roots

1≠

2, we may take

αn1(t)=er

t, αn2(t)=er

The particular integral is best found with the method of undetermined coefficients. If we substitute

αnp(t)=d

Sin

ωt+d

cos

ωt

into the differential equation, then we require

Equating the coefficients of the trigonometric terms we find

For

>0 this equation has a unique solution so that

and

may be assumed known. Finally, we

need to determine the coefficients

and

so that

αn(t)

satisfies the initial conditions. We obtain

the conditions

n+C

n=− d

n+r2C

n=−ωd

As long as

≠r

2 this system has the unique solution

< previous page page_173 next page >

page_174

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_174.html[22/02/2009 23:53:16]

< previous page page_174 next page >

Page 174

so that

It is possible that for some index A: the two roots

1 and

2 are the same. Then the first term for αk(t)

is indeterminate and must be evaluated with 1’Hospital’s rule. In analogy to mechanical systems we may

say that the nth mode of our approximate solution is overdamped, critically damped, or underdamped if

is positive, zero, or negative, respectively. Using the trigonometric identities already

employed in Example 7.1 (or complex exponentials) we see from

that the term

contributes traveling waves moving right and left with speed and wave length For

the complementary solution in an overdamped or critically damped mode adds an exponentially decaying

stationary solution of the form

For sufficiently large n the nth mode will be underdamped because

as If we write

αn(t)=A

ner

1t+

A2ner

αnp(t)

where

then the complementary part of

contributes terms like

which describes exponentially decaying traveling waves moving right and left with speed wave length

We note that if we write

formally as a plane wave

ei(kx−δt)

then

λn

and

< previous page page_174 next page >

page_175

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_175.html[22/02/2009 23:53:17]

< previous page page_175 next page >

Page 175

It follows that

This equation is known as the dispersion relation for the telegraph equation. Conversely, any plane

wave satisfying the dispersion relation is a solution of the unforced telegraph equation on the real line

(for a discussion of the meaning and importance of dispersion see, e.g., [3]).

Example 7.5 Oscillations of a hanging chain.

This example shows that special functions like Bessel functions also arise for certain problems in

cartesian coordinates. A chain of length

with uniform density is suspended from a (frictionless) hook

and given an initial displacement and velocity which are assumed to lie in the same plane. We wish to

study the subsequent motion of the chain.

Let

u(x, t)

be the displacement from the equilibrium position where the co-ordinate

is measured from

the free end of the chain at

=0 vertically upward to the fixed end at

x=L.

Then the tension in the chain

is proportional to the weight of the chain below

After scaling, Newton’s second law leads to the

following mathematical model for the motion of the chain [4]:

u(L, t)

u(x,

0)=

(x)

ut(x,

)

(x).

The associated eigenvalue problem is

If we add the natural restriction that also

then we again have a singular Sturm-Liouville

problem. Its solution is not obvious, but the arguments of Section 3.2 imply that all eigenvalues are

necessarily nonpositive so that

=−λ2.

< previous page page_175 next page >

page_176

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_176.html[22/02/2009 23:53:17]

< previous page page_176 next page >

Page 176

If we rewrite the eigenvalue problem in the form

and match it against formula (3.10), we find immediately that it has the solutions

where and where As before,

0 is the

th zero of the zero order Bessel function

(z).

In summary, the eigenvalue problem associated with the hanging chain has the solution

with

We also know from our discussion of Example 6.10 that for

so that the eigenfunctions

are orthogonal in L2(0, L). (We note that orthogonality with respect to

the weight function

w(x)

=1 is predicted by the Sturm-Liouville theorem of Chapter 3 if the eigenvalue

problem were a regular problem given on an interval

with The approximate solution is written

Substitution into the wave equation leads to the initial value problems

and the approximate solution

In Fig. 7.5 we show several positions of the chain as it swings from its initial straight-line displacement

on the left to its maximum displacement on the right.

< previous page page_176 next page >

page_177

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_177.html[22/02/2009 23:53:18]

< previous page page_177 next page >

Page 177

Figure 7.5: Position of the hanging chain as its end swings from its initial position to the right. The

displacement

u(x, t)

is shown for

0, .5, 1, 1.5, 2, 2.4; at

=2.4,

=(0, 2.4)≈0,

=4,

=1.

Example 7.6 Symmetric pressure wave in a sphere.

At time

0 a spherically symmetric pressure wave is created inside a rigid shell of radius

We want to

find the subsequent pressure distribution in the sphere.

Since there is no angular dependence, the mathematical model for the pressure

(r,

) in the sphere is

We shall assume that the initial state can be described by

(

0)=

(r)

(

0)=

(r).

At all times we have to satisfy the symmetry condition

(0,

)=0.

Since the sphere is rigid, there is no pressure loss through the shell so we require

ur(R, t)

=0.

< previous page page_177 next page >

page_178

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_178.html[22/02/2009 23:53:19]

< previous page page_178 next page >

Page 178

The eigenvalue problem associated with this model is

To ensure a finite pressure we shall require that

We encountered an almost identical problem

in our discussion of heat flow in a sphere (Example 6.7) and already know that bounded solutions for

nonzero λ have to have the form

The boundary condition at

r=R

requires that

Hence the eigenvalues are determined from the roots of

The existence and distribution of roots of f were discussed in Example 6.6. We see by inspection that

so that there are count ably many roots, and that

because the cosine term will dominate for large

In addition we observe that for the boundary

conditions of this application λ0=μ0=0 is an eigenvalue with eigenfunction

It follows from the general theory that distinct eigenfunctions are orthogonal in

2(0,

r2). This

orthogonality can also be established by simple integration. We see that for λm≠λ

in view of

(λm)=

(λn)=0. It is straightforward to verify that this conclusion remains valid if

=0 and

≠0. It follows that

< previous page page_178 next page >

page_179

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_179.html[22/02/2009 23:53:20]

< previous page page_179 next page >

Page 179

where for

≥0

Note that

0(0) and are the average values for the initial pressure and velocity over the sphere.

The equations for

αn(t)

are readily integrated. We obtain

For example, let us suppose that

=1 and

and

(r)

.= 0.

Then

and

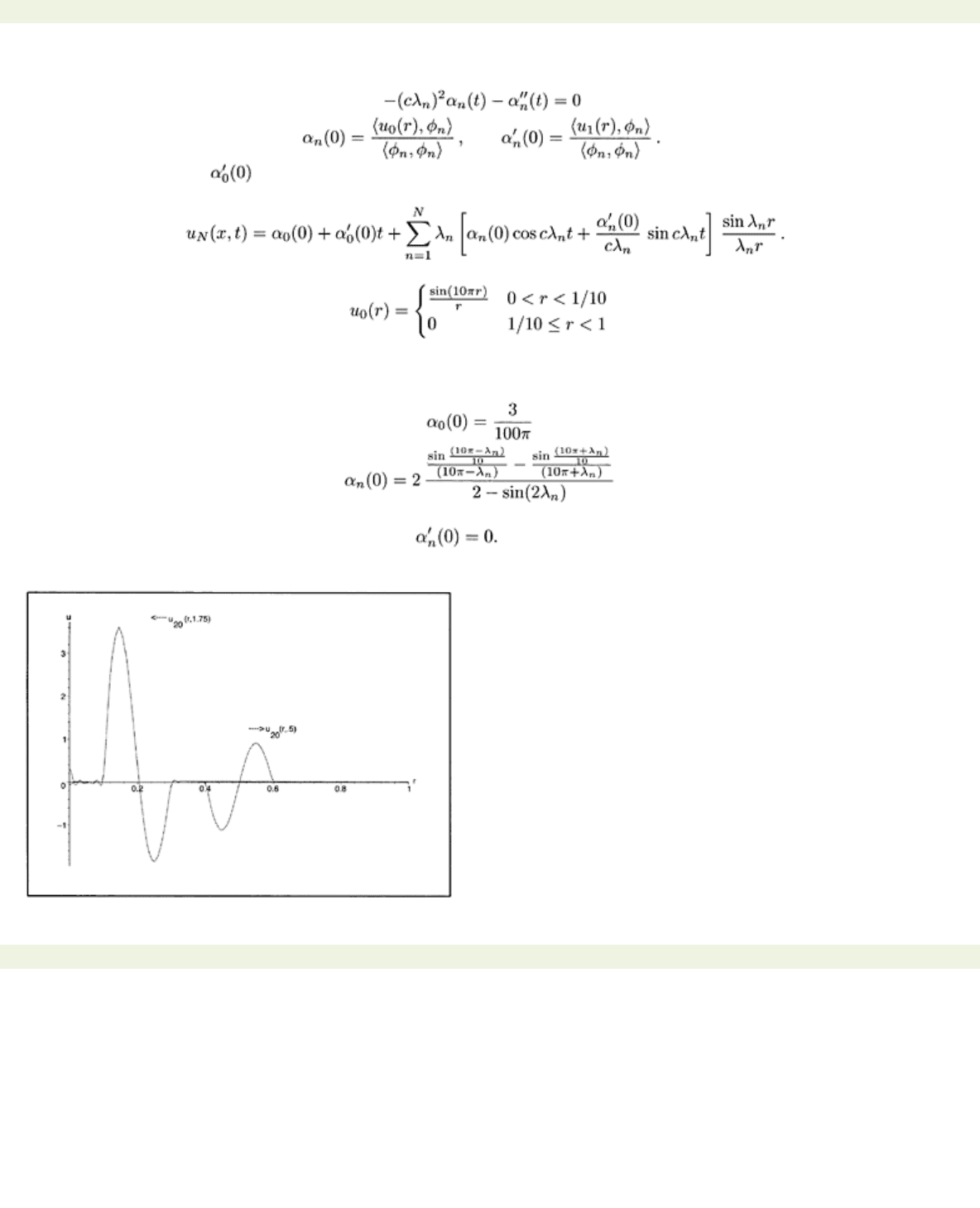
Fig. 7.6 shows the pressure wave

(r, t)

at time

=.5 before it has reached the outer shell at

and after reflection at

1.75.

Figure 7.6: Pressure wave

(r, t)

.5 and after reflection at

=1.75.

< previous page page_179 next page >

page_180

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_180.html[22/02/2009 23:53:21]

< previous page page_180 next page >

Page 180

Example 7.7 Controlling the shape of a wave.

The next example is reminiscent of constrained Hilbert space minimization problems discussed, for

example, in [15]. The problem will be stated as follows.

Determine the “smallest” force

F(x, t)

such that the wave

u(x, t)

described by

uxx−utt=F(x, t)

(0,

u(L, t)

(

0)=

(

0)=0

satisfies the final condition

u(x, T)=uf(x)

ut(x, T)

where

uf(x)

is a given function and

is a given final time.

We shall ignore the deep mathematical questions of whether and in what sense this problem does

indeed have a solution and concentrate instead on showing that we can actually solve the approximate

problem formulated for functions of

which at any time belong to the subspace

As before

is the

th eigenfunction of

i.e., To make the problem tractable we shall agree that the size of the force will

be measured in the least squares sense

The approximation to the above problem can then be formulated as:

Find

such that

for all

for which the solution

< previous page page_180 next page >

page_181

file:///G|/%5EDoc%5E/_new_new/got/020349878X/files/page_181.html[22/02/2009 23:53:21]

< previous page page_181 next page >

Page 181

(0,

)

=u(L, t)

(

0)=

(

0)=0

satisfies

u(x, T)

PNuf(x)

ut(x, T)=0.

We know that

and

have the form

and

where

The variation of parameters solution for this problem can be verified to be

uN(x, T)

will satisfy the final condition if γn(£) is chosen such that

Hence

γn(t)

must be found such that

(7.9)

(7.10)

Finally, we observe that

< previous page page_181 next page >