Буховец А.Г. и др. Статистический анализ данных в системе R
Подождите немного. Документ загружается.

2.6. Наиболее распространённые распределения 41
−6 −4 −2 0 2 4 6
0.0 0.5 1.0 1.5
N(0, 0.25)
N(0, 0.5)
N(0, 1)
N(0, 2)
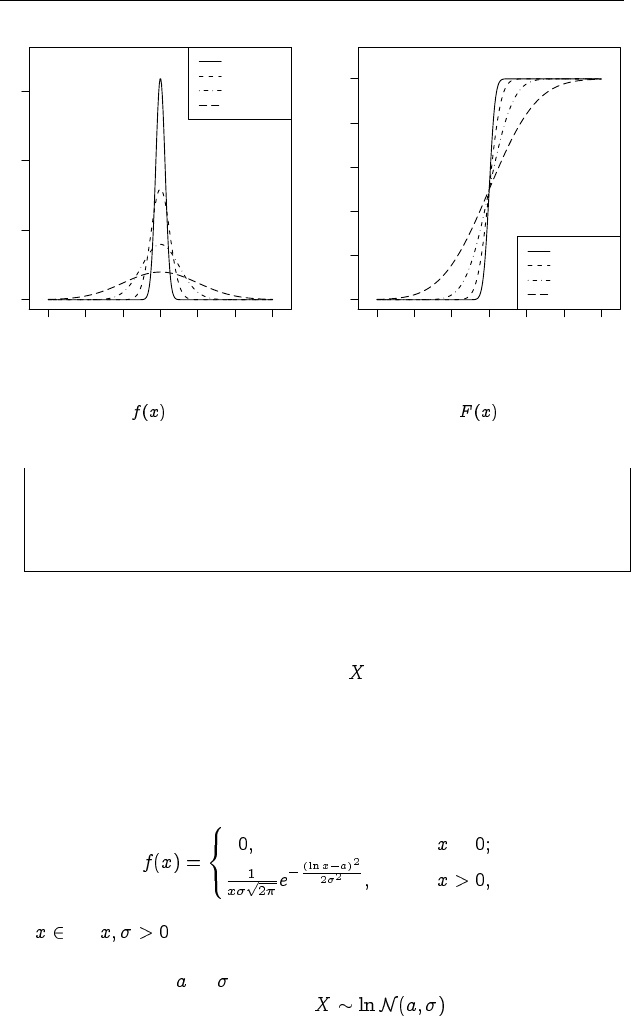
Рис. 2.11. Плотность нормального
распределения
−6 −4 −2 0 2 4 6
0.0 0.2 0.4 0.6 0.8 1.0
N(0, 0.25)
N(0, 0.5)
N(0, 1)
N(0, 2)
Рис. 2.12. Функция нормального
распределения
37 > f <- sapply(s, function(ss) dnorm(x, a, ss))
38 > F <- sapply(s, function(ss) pnorm(x, a, ss))
39 > l <- sapply(s, function(ss) sprintf("N(%.3g, %.3g)", a, ss))
40 > cgraph(x, f, l)
41 > fgraph(x, F, l)
2.6.7. Логнормальное распределение
Непрерывная случайная величина имеет логарифмически нор-
мальное или логнормальное распределение, если её логарифм нор-
мально распределён. Подобно нормальному распределению логнор-
мальное возникает при рассмотрении произведения большого числа
независимых случайных величин с конечной дисперсией. Плотность
вероятности логарифмически нормального распределения имеет вид:
если 6
если
где R; .
Логарифмически нормальное распределение полностью определя-
ется параметрами и . Функция распределения логарифмически
нормальной случайной величины имеет вид:
42 2. Сведения из теории вероятностей
где –– функция Лапласа.
Математическое ожидание и дисперсия логарифмически нормаль-
ной случайной величины зависимы:
M D M
0 1 2 3 4 5 6
0.0 0.5 1.0 1.5
ln N(0, 0.25)
ln N(0, 0.5)
ln N(0, 1)
ln N(0, 2)
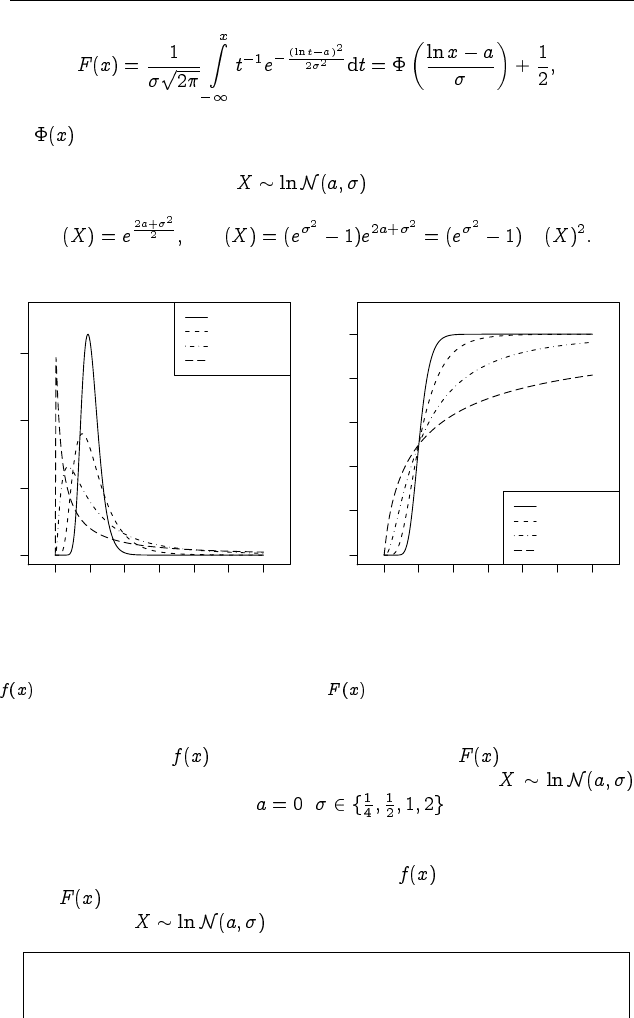
Рис. 2.13. Плотность логарифми-
чески нормального распределения
0 1 2 3 4 5 6
0.0 0.2 0.4 0.6 0.8 1.0
ln N(0, 0.25)
ln N(0, 0.5)
ln N(0, 1)
ln N(0, 2)
Рис. 2.14. Функция логарифми-
чески нормального распределения
На рис. 2.13 и 2.14 показаны примеры построения графиков плот-
ности вероятности и функции распределения логарифмиче-
ски нормально распределённой случайной величины
при значениях параметров: , .
Пример 2.7. Продолжая предыдущий пример, построим вышепри-
ведённые графики плотности вероятностей и функции распреде-
ления для логарифмически нормально распределённой случай-
ной величины с помощью R.
42 > a <- 0; s <- c(1/4, 1/2, 1, 2)
43 > x <- seq(a, a+3*max(s), len=300)
44 > f <- sapply(s, function(ss) dlnorm(x, a, ss))
- 2008 — 2025 «СтудМед»

