Bryan L. Programmable controllers. Theory and implementation
Подождите немного. Документ загружается.


639
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
V
C
idt
C
VV
R
dt
C
V
R
dt
C
V
R
dt
RC
Vdt
RC
Vdt
RC
Vdt V dt
t
t
in
tt
tt
tt
out
in out
out
in out
in out
=
=−
(
)
=−
=−
=−
∫
∫
∫∫
∫∫
∫∫
1
11
11
11
1
0
0
00
00
00
(a) To obtain the differential equation of this network, we must take the
derivative of both sides of the output voltage equation to eliminate the
integral terms:
dV
dt RC
VV
VRC
dV
dt
V
out
in out
in
out
out
=−
(
)
=+
1
(b) The Laplace form of this first-order differential equation is:
V RCsV V V
ssts
in( ) out( ) out( ) out( )
=−+
=0
Since there is no initial value at
t
= 0, this equation becomes:
V RCsV V
V RCs
sss
s
in( ) out( ) out( )
out( )
=+
=+
(
)
1
The transfer function is:
V
V sRC
s
s
out( )
in( )
=
+
1
1
The equation for a first-order system with lag is represented by:
Hp
s
s
()
=
+
1
1
τ
Therefore, this electrical network is a first-order lag system where the
time constant
τ is equal to
RC
(the resistance times the capacitance).
(c) Figure 14-34 shows the block diagram of this closed-loop system.
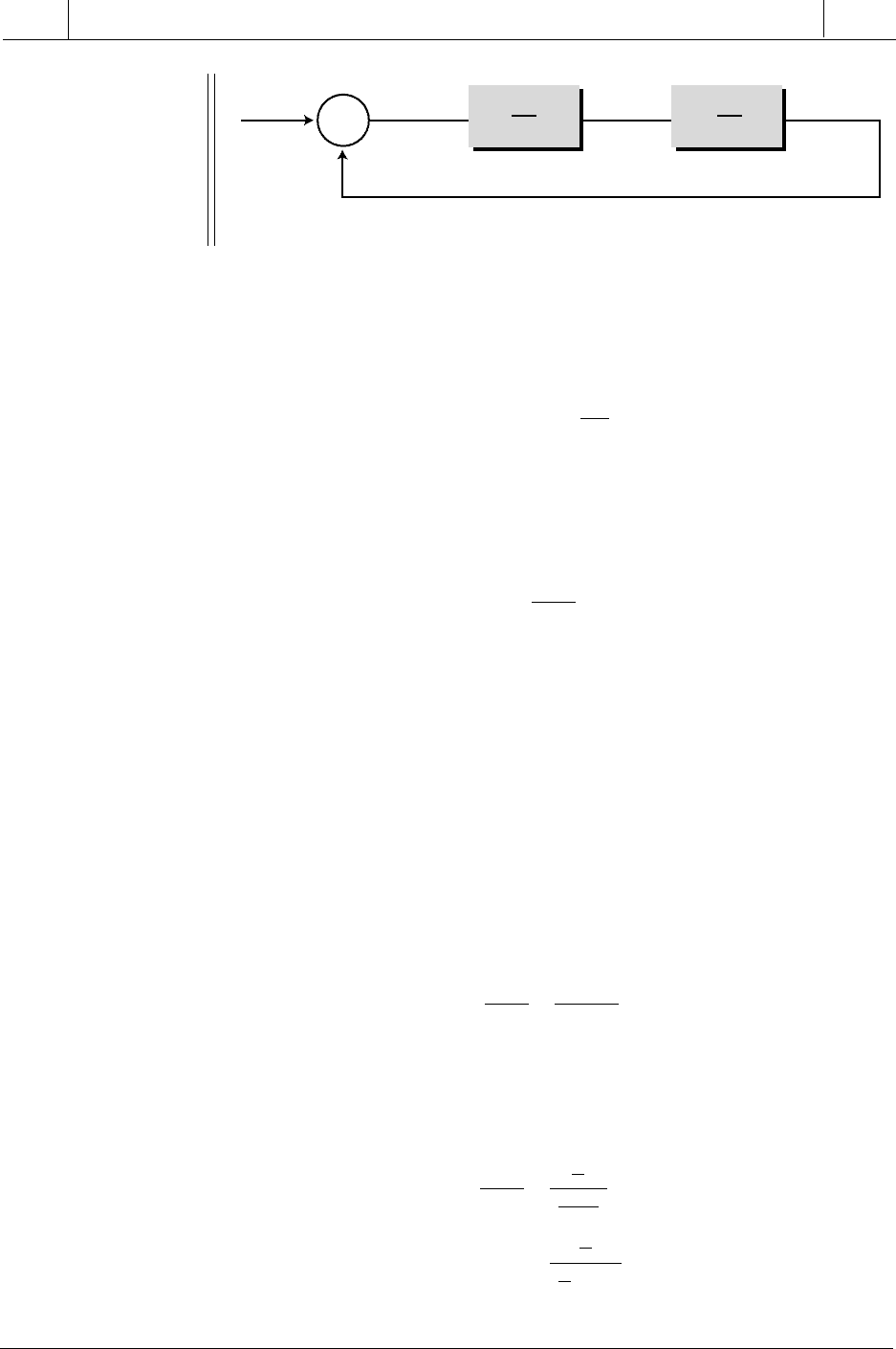
640
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
Figure 14-34. Block diagram of the R/C network.
Referring to the hot-water heater example used in Section 14-3, let’s assume
that the differential equation that describes the process, otherwise known as
the heating system’s enthalpy balance equation, is given by:
Steam flow = A
dT
dt
BT
t
+
()
where A and B are constants and T is the temperature. Since the steam flow
is directly related to the control variable and the temperature is the process
variable, we can rewrite this equation as:
CV A
dPV
dt
BPV
tt() ()
= +
Taking the Laplace transform of this equation, we get:
CV AsPV APV BPV
sst s() () ( ) ()
= −+
=0
Assuming that the value of PV at t = 0 is zero, this equation becomes:
CV AsPV BPV
PV As B
sss
s
() () ()
()
()
= +
=+
The process’s transfer function, which is equal to the process’s output divided
by its input, is:
PV
CV As B
s
s
()
()
=
+
1
To obtain a standard first-order lag equation (i.e., a fraction whose denomina
-
tor is τs + 1), we can divide both the numerator and the denominator by B:
PV
CV
s
s
s
B
As B
B
B
A
B
()
()
=
()
()
=
()
+
()
+
1
1
1
V
in(
s
)
–
V
out(
s
)
V
out(
s
)
V
out(
s
)
V
in(
s
)
I
(
s
)
+
–
Σ
1
R
1
Cs

641
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Figure 14-35. Integral transfer function.
Previously, we calculated experimentally that the gain for this process is
0.8°C/% and that it took 15 minutes to achieve the final steady-state value.
Furthermore, as we will discuss in Section 14-6, it is a given that in a first-
order system with lag the output variable will be at 99.33% of the input
variable when t = 5τ. The observed value of the response at 15 minutes is
100%,
which is close to the 99.33% at 5τ. Therefore, we can approximate the
value of τ as:
515
15
3
τ
τ
≈
≈≈
min
min
5
min
Thus, we can represent the process’s transfer function as:
PV
CV s
s
s
()
()
.
=
+
08
31
INTEGRAL LAPLACE TRANSFORMS
Aside from a simple constant gain, an integral transfer function represents
the simplest of all process responses (see Figure 14-35). It is represented by
the equation:
Output
Input
==
=
=
∫
∫
∫
PV
CV
Adt
Adt
PV A CVdt
t
t
t
0
0
0
where A is a constant gain. In Laplace, the term (
A
s
) replaces the time domain
integral term. Therefore, the Laplace transform of this equation is:
Input
CV
Output
PV
Integral
Process
∫Input

642
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
PV
A
s
CV
ss() ()
=
An integral process integrates the input with the process over time. This
implies that the rate of change of the process output varies according to the
input, as shown in the following equation:
PV A CVdt
dPV ACVdt
dPV
dt
ACV
t
=
=
=
∫
0
Therefore, in an integral process, a change in the control variable will
produce a rate of change in the process variable over time.
In process systems, changes in the control variable are usually simulated by
producing a step change with amplitude B. In Laplace form, a step change to
an integral process is represented as:
PV CV
A
s
B
s
A
s
AB
s
=
=
=
2
where:
A
B
=
=
the constant integral gain
the amplitude of the step change
The inverse Laplace (time domain) response of this equation is:
PV ABt
t()
=
This implies that the rate of increase of the process variable is AB per second
(or per minute, depending on time units). Figure 14-36 illustrates this integral
response curve, which is a ramp-type function.
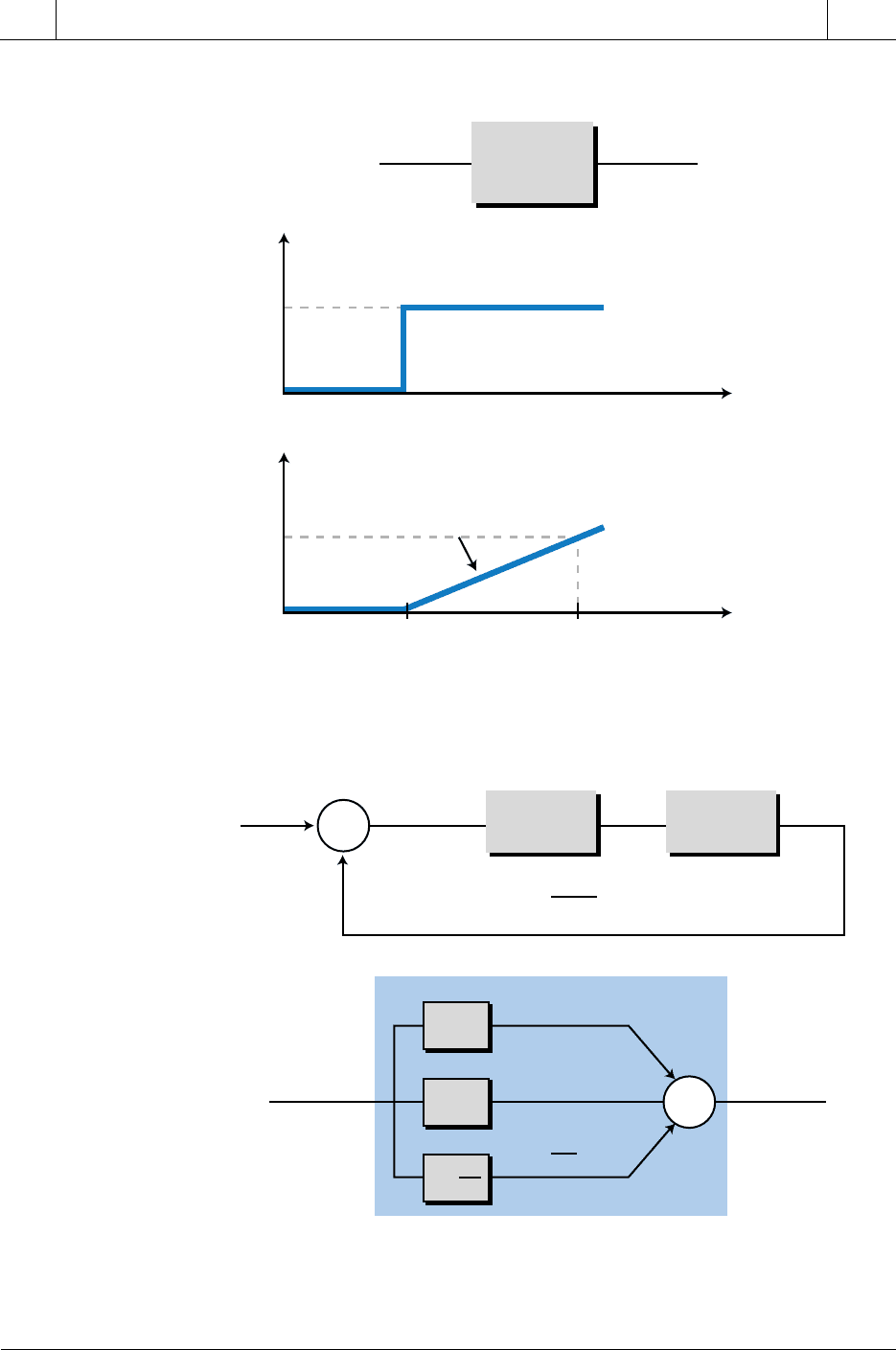
As we discussed briefly in Chapter 8, the following integro-differential
equation describes the output (i.e., control variable) of a typical propor-
tional-integral-derivative (PID) controller (see Figure 14-37):
643
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Figure 14-36. Integral response to a step change.
Figure 14-37. PID process control loop.
CV
CV
B
t
(sec or min)
PV
Integral
Process
∫
A dt
PV
AB
t
(sec or min)
Rate of output
increase
AB
t
0
t
1
= 1
Controller Process
E
=
SP
–
PVSP CV
CVE
PV
PV
+
–
Σ
Hc
(
s
)
=
Hc
(
s
)
Hp
(
s
)
CV
(
s
)
E
(
s
)
Σ
K
P
K
I
K
P
E
K
I
∫
Edt
K
D
I
D
P
+
+
+
d
dt
K
D
dE
dt
0
t

644
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
CV K E K Edt K
dE
dt
CV
tP I
t
Dt() ( )
=+ + +
∫
=
0
0
where:
CV
K
ESPPV
K
K
t
P
I
D
()
)
=
=
−
=
=
the control variable output
the proportional gain
= the error (
the integral gain
the derivative gain
To find the Laplace transform of this PID equation, we must make the
appropriate substitutions, assuming that the initial parameters are zero,
which yields:
CV K E
KE
s
KEs
sPs
Is
Ds() ()
()
()
=++
Therefore, the transfer function of a PID controller (Hc) in Laplace is:
Hc
CV
E
CV K E
KE
s
KE s
CV
E
K
K
s
Ks
s
s
s
sPs
Is
Ds
s
s
P
I
D
()
()
()
() ()
()
()
()
()
==
=++
=++
Out
In
14-5 DEAD TIME RESPONSES IN LAPLACE FORM
Until now, we have only discussed Laplace transforms of ideal processes. In
reality, however, no process is ideal. Most processes contain either dead time,
lag time, or both. Therefore, these factors must be accounted for when
analyzing a process’s transfer function and performing its Laplace transform.
Dead time involves a shift, or displacement, of the time variable t, meaning
that the process input occurs at time t but the output does not occur until time
t
d
. The Laplace transform of a dead time factor is
e
ts
d
−
, where t
d
is the delay
of the output response and e is a constant equal to 2.718.
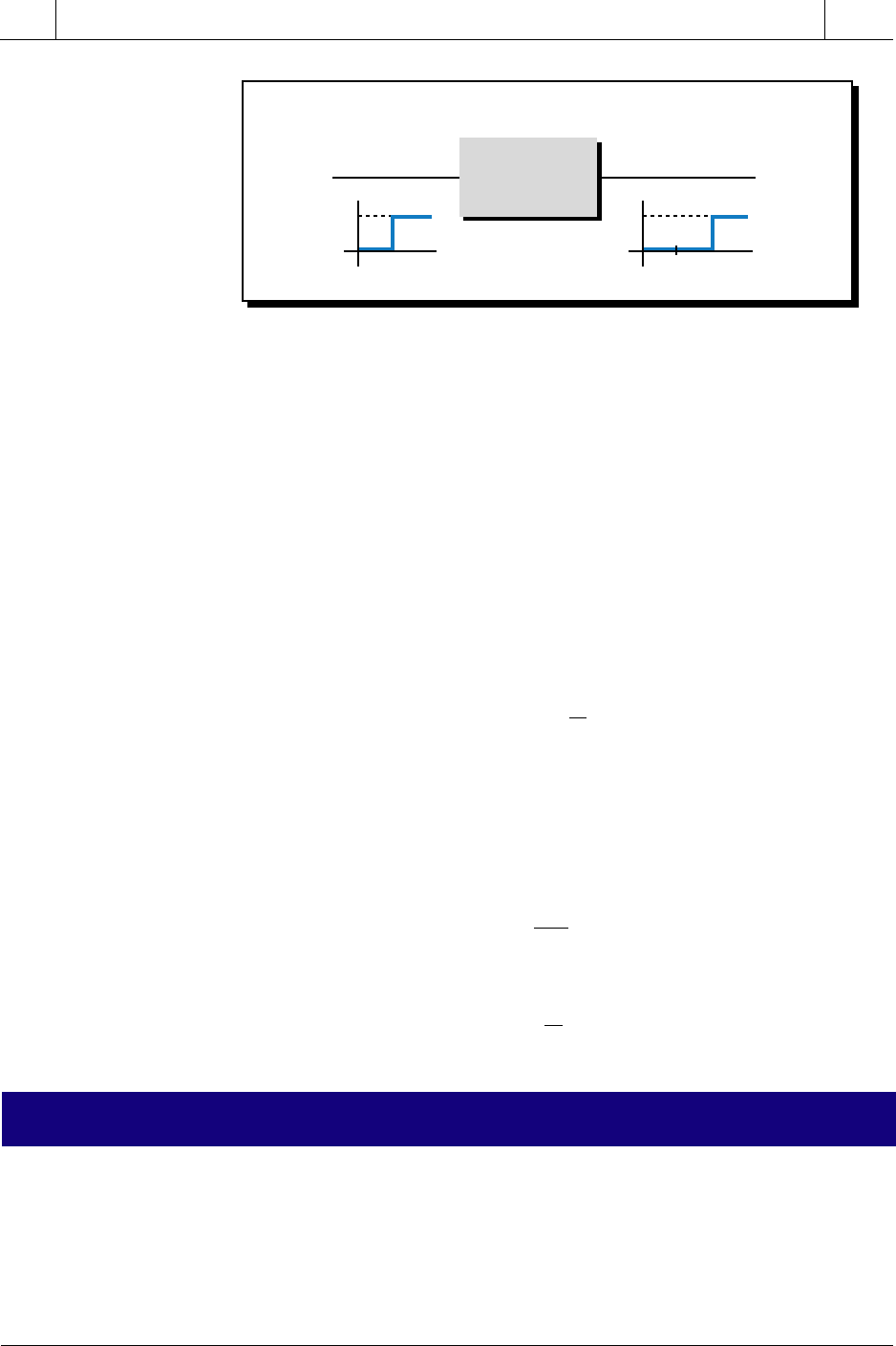
Figure 14-38 illustrates a transfer function of a simple system with dead
time (and no lag), which receives a step (OFF-to-ON) input with amplitude
A. Note that the value of the process gain is 1, because an input of magnitude
645
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Figure 14-38. Transfer function of a system with dead time.
A yields an output of magnitude A. The output, however, has a dead time
equal to t
d
. Therefore, the transfer function Hp is equal to the process gain
times the dead time. If the process gain equals 1, then the Laplace transform
of this transfer function is:
Hp e
s
ts
d
()
=
−
The input (CV) to the process in Figure 14-38 is a step input of amplitude A.
In the previous section, we explained that the Laplace transform of a step
input is:
CV
A
s
=
Knowing these two equations, along with the fact that Hp is equal to the
output divided by the input, we can find the value, in Laplace, of the process
variable:
Hp
PV
CV
PV CV Hp
A
s
e
ts
d
=
=
=
−
()()
14-6 LAG RESPONSES IN LAPLACE FORM
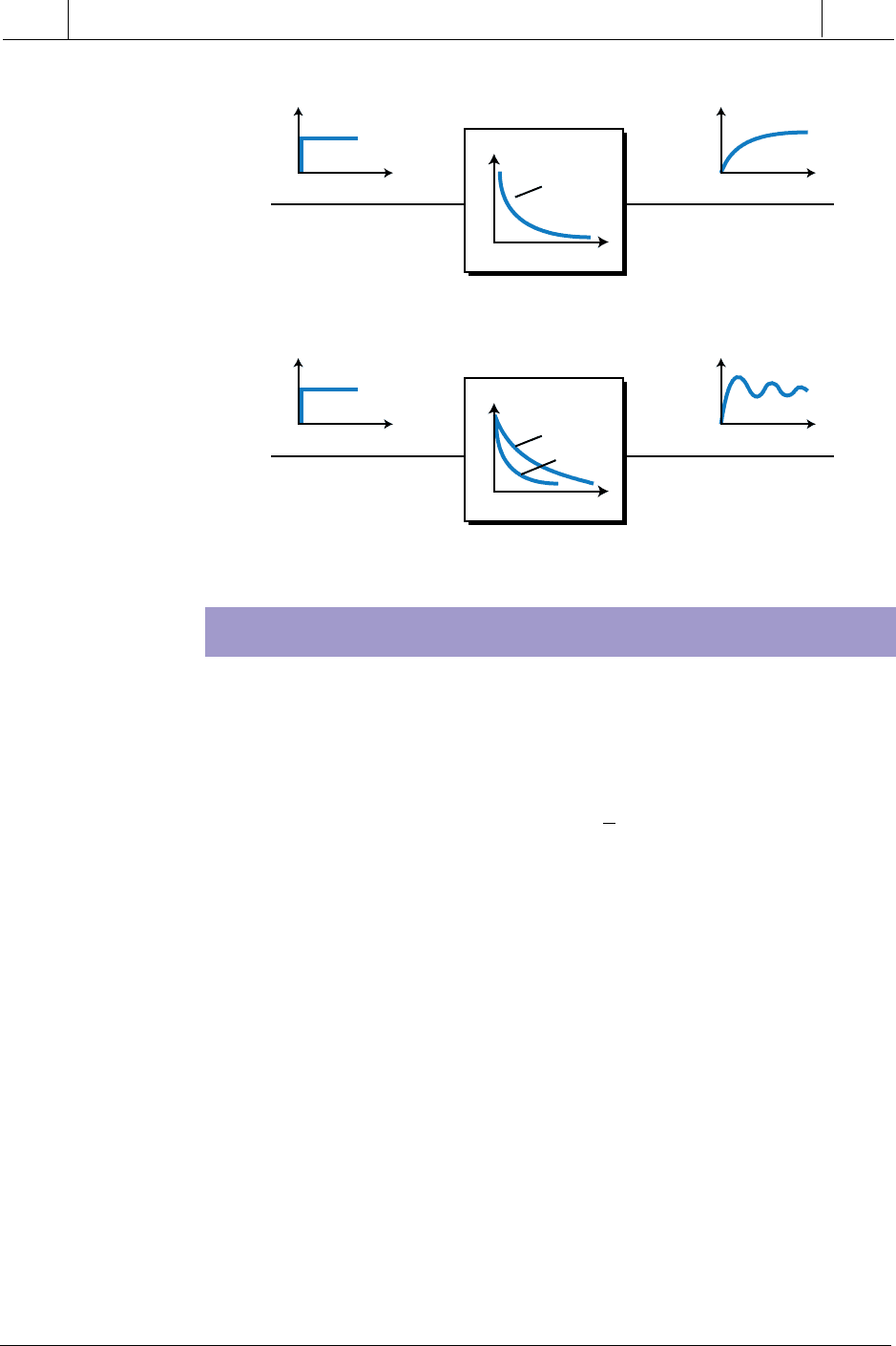
Now that we have explained the basics of Laplace transforms, let’s examine
the various responses exhibited by processes. Most processes exhibit either
a first-order or second-order lag response with one or two time lags, respec-
tively (see Figure 14-39). Note that this figure shows open-loop processes
whose inputs are the control variable from the controller.
Input Output
Hp
Process
A
t
A
tt
d
CV PV
646
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
Figure 14-39. First- and second-order lags.
First-Order
Process
Second-Order
Process
PVCV
PVCV
τ
τ
1
τ
2
FIRST-ORDER LAG RESPONSES
First-order lag is one of the most common types of process responses. In this
type of system, the process variable response lags behind a rapid change (step
change) in the control variable. In the time domain, a first-order response to
a step input is represented by the equation:
VV e
t
out in
=−
()
−
1
τ
where:
V
V
t
in
out
the step input to the process
the output of the process
time
the time constant
=
=
=
=
τ
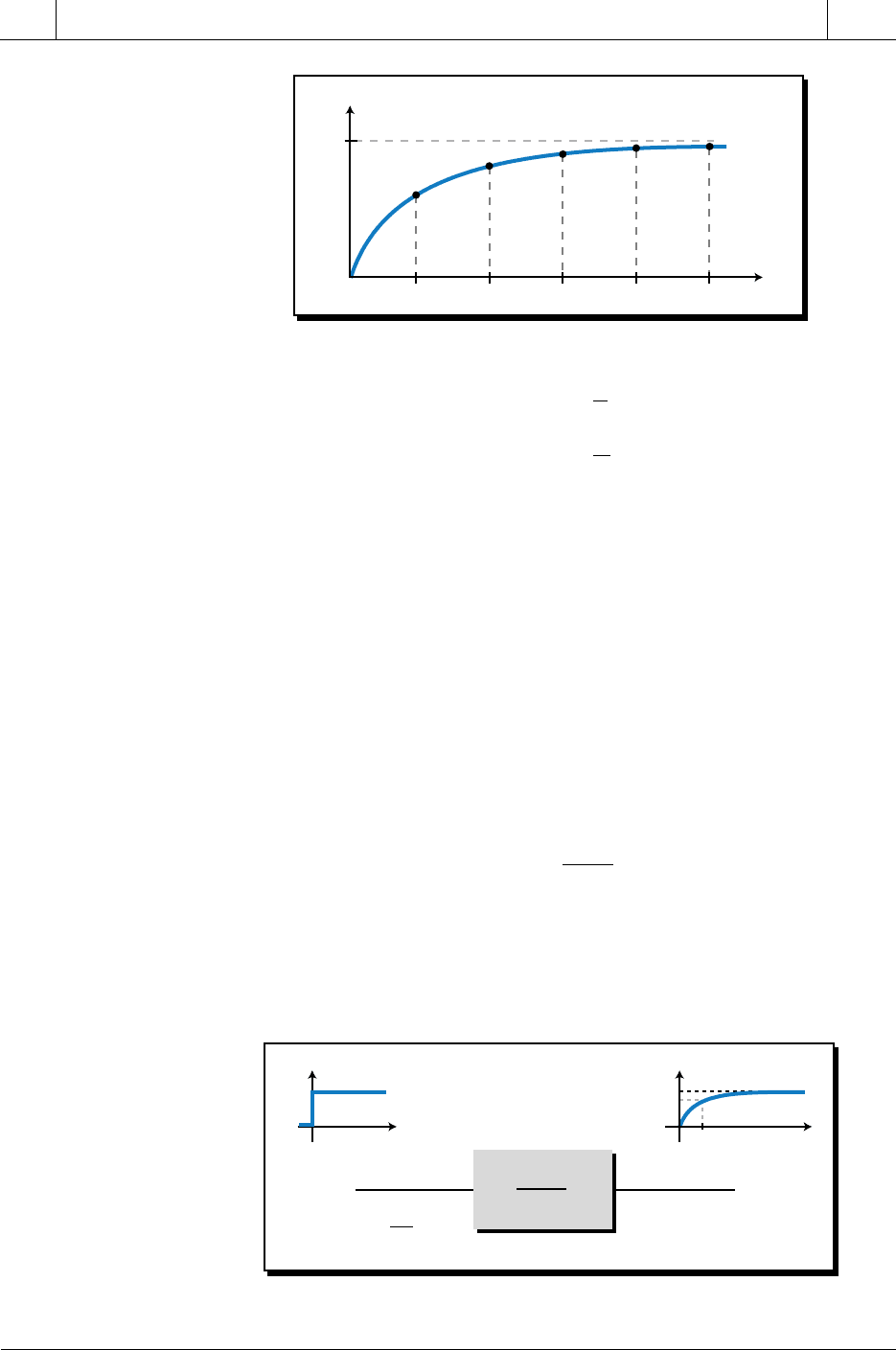
As shown in Figure 14-40, this response is an exponential function, meaning
that the value of V
out
increases rapidly with time to equal V
in
. The time
constant τ describes how quickly the output catches up with the input value—
the smaller the value of τ, the faster V
out
equals V
in
and vice versa. So, first-
order responses with smaller time constants have shorter lag times.
For a first-order system with a step input and lag, the value of the output,
given that t = τ, is 63.2% of the input is:
647
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Figure 14-40. First-order lag process response.
Figure 14-41. First-order transfer function with lag in the Laplace domain.
VV e
Ve
Ve
V
V
t
out in
in
in
in
in
=−
()
=−
()
=−
()
=−
()
=
−
−
−
1
1
1
1 0 368
0 632
1
τ
τ
τ
.
.
As the value of t increases, the value of V
out
becomes closer to 100% of V
in
.
As shown in Figure 14-40, at the time t = 4τ, the value of V
out
will be over 98%
of that of V
in
, and when the time variable reaches 5τ, V
out
will be over 99%
of V
in
.
In the Laplace domain, a first-order system transfer function with lag is
represented by the equation (see Figure 14-41):
Hp
A
s
s()
=
+
1
1
τ
where:
A
1
= the process amplitude gain
= the system’s lag time
τ
In Out
A
1
τ
s
+ 1
In
(
s
)
=
A
2
s
A
t
A
t
= 1τ
Hp
V
in
V
out
t
= 1τ
t
= 3τ
t
= 4τ
t
= 5τ
t
= 2τ
0.632
0.865
0.950
0.982
0.993
t
648
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
Out
t
t
0
Process transfer function [
Hp
(t)
]
A
1
τ
A
1
τ
τ
e
–t
0.368
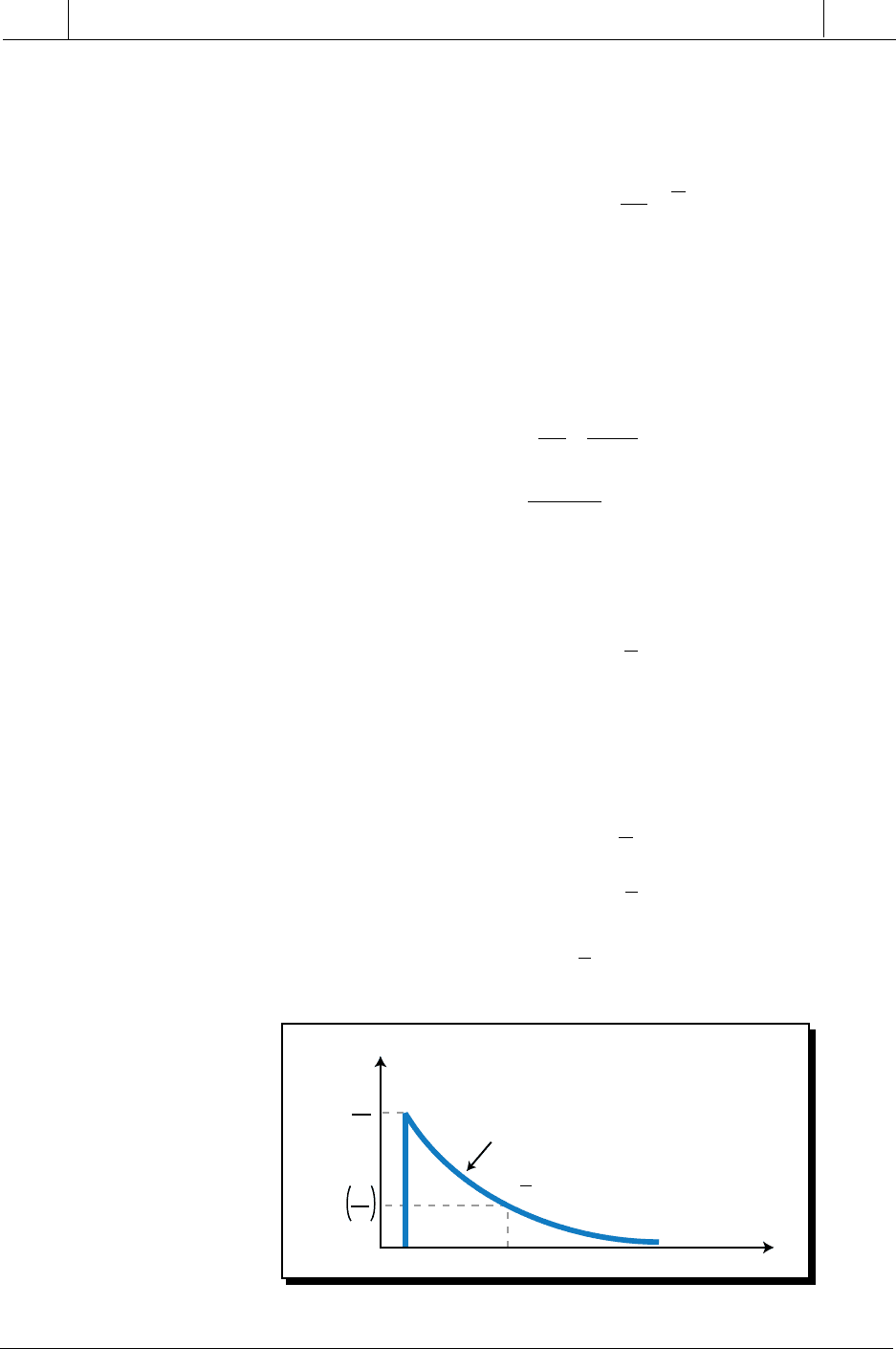
t
= τ
Figure 14-42. Process transfer function in the time domain.
Using Table 14-2, the inverse Laplace transform (represented by L
–1
) of this
transfer function, which turns the Laplace equation into a time-based transfer
function, is:
L
–
() ()
[]
1
1
Hp Hp
A
e
st
t
==
−
τ
τ
This response, as shown in Figure 14-42, has a decaying form (i.e., it
decreases over time) due to the term e. This same system given a step input
with amplitude A
2
would have the equation:
Out In
() () ()
()
sss
Hp
A
s
A
s
AA
ss
=
()( )
=
+
=
+
21
12
1
1
τ
τ
Again using Table 14-2, the inverse Laplace response, or real-time response
of the system (Out
(t)
), is:
Out
()
–
t
t
AA e=−
12
1
τ
where the value of the output will be 0.63A
1
A
2
(63% of A
1
A
2
) when t = τ. If
the input is a unit step (that is, the amplitude A
2
equals 1) and the gain of
Hp
(s)
equals 1 (A
1
= 1), then the output will be:
Out
t
t
AA e
e
e
t
t
()
−
=−
()
=
()()
−
=−
−
−
12
1
111
1
τ
τ
τ
