Bryan L. Programmable controllers. Theory and implementation
Подождите немного. Документ загружается.

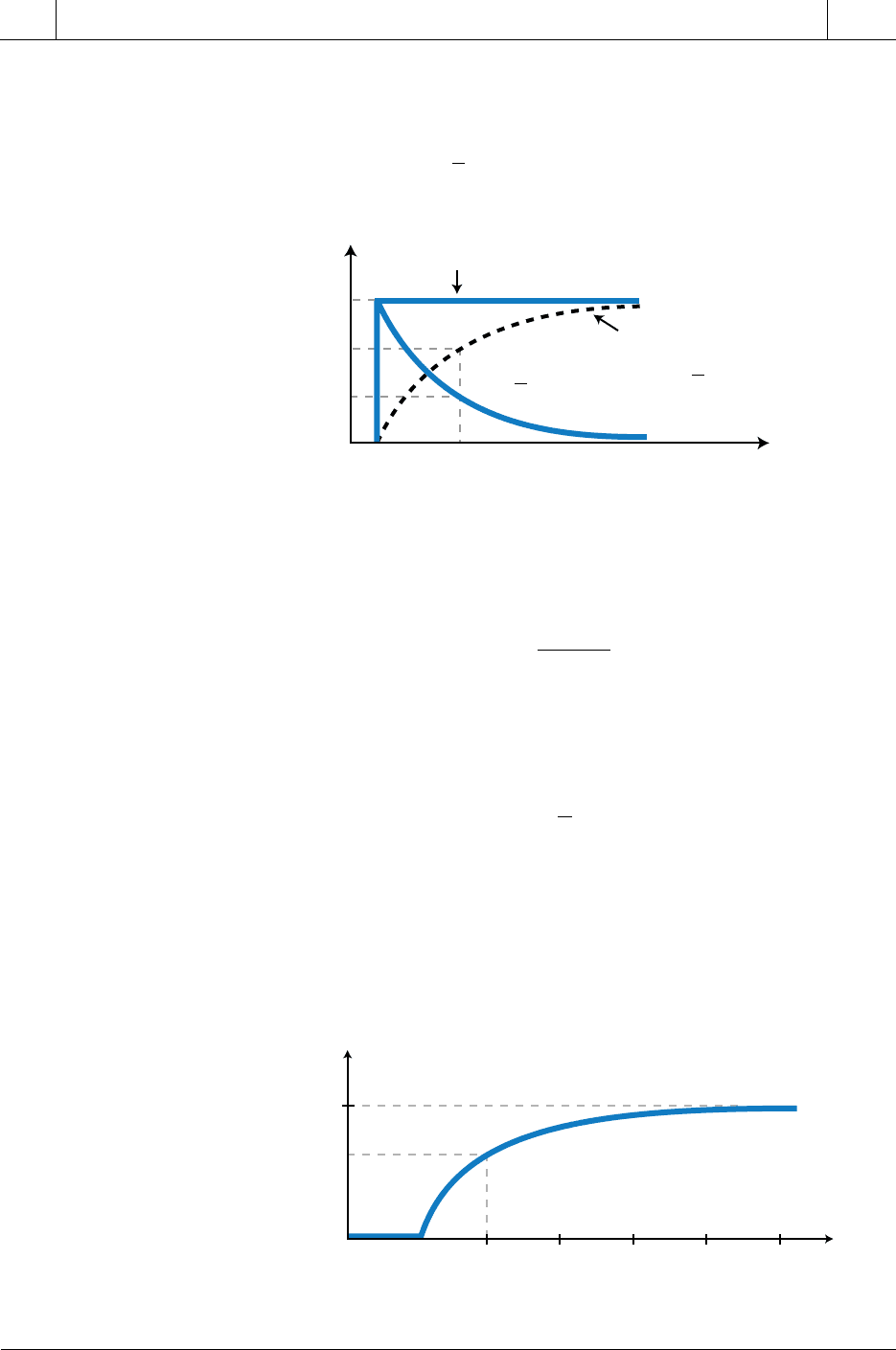
649
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Out
t
t
0
t
= τ
Step Input
1 –
e
1
0.632
0.368
First-Order Response
to Step Input
(Process)
τ
e
–t
τ
–t
Figure 14-43. Process variable’s lag response.
Figure 14-44. First-order step response with dead time and lag.
Figure 14-43 graphs the response of the process variable Out
(t)
for A
1
= A
2
=
1. This curve, representing a first-order response to a step input plus lag, is a
function of the system’s transfer function, which is the step value (1) minus
the system’s curve term (
e
t−
τ
).
Adding a simple dead time term (
e
ts
d
−
) to a first-order step response with lag
generates the Laplace transfer function:
Out
()
()
s
ts
AA
ss
e
d
=
+
−
12
1
τ
where t
d
is the dead time. Figure 14-44 shows the graph of this function in
the time domain. The value of the output is:
Out for
Out for
()
–
()
t
t
d
t
d
AA e t t
tt
=−
≥
=<
12
1
0
τ
Note that the first output response equation is valid for t values greater than
t
d
, the dead time. Out
(t)
will be zero for time values before the dead time t
d.
A
1
A
2
0.632
A
1
A
2
t
d
+ 1τ
t
d
t
d
+ 3τ
t
d
+ 4τ
t
d
+ 5τ
t
d
+ 2τ
t

650
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
EXAMPLE 14-4
A process system has a first-order response with a time constant of
10.8 minutes. (a) Calculate how long it will take for the value of the
output
V
out
to be at 90% of the input
V
in
. (b) Calculate the value of
V
out
at 90% of
V
in
given a 5 minute dead time.
S
OLUTION
(a) A first-order system with lag has a response of:
The value of τ is 10.8 seconds and the required ratio of output over
input is 90%, or 0.90; therefore:
Solving for
t
by taking the natural logarithm (ln) of both sides of the
equation yields:
So, in 24.87 minutes, the value of the output will be at 90% of the value
of the input.
(b) The dead time will simply add to the time required to achieve the
90% value. Therefore, with a lag of 5 minutes, the system will reach a
value of 90% final output in 29.87 minutes (24.87 min + 5 min).
VV e
t
out in
=−
−
1
τ
VV e
V
V
e
e
e
t
t
t
t
out in
out
in
=−
=−
=−
=−
=
−
−
−
−
1
1
090 1
1090
010
10 8
10 8
τ
τ
.
.
.
.
.
e
t
t
t
−
=
−
=
−=
=−
=
10 8
010
10 8
010
10 8 0 10
10 8 2 303
24 87
.
.
.
ln .
( . )(ln . )
(.)(. )
. minutes
651
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
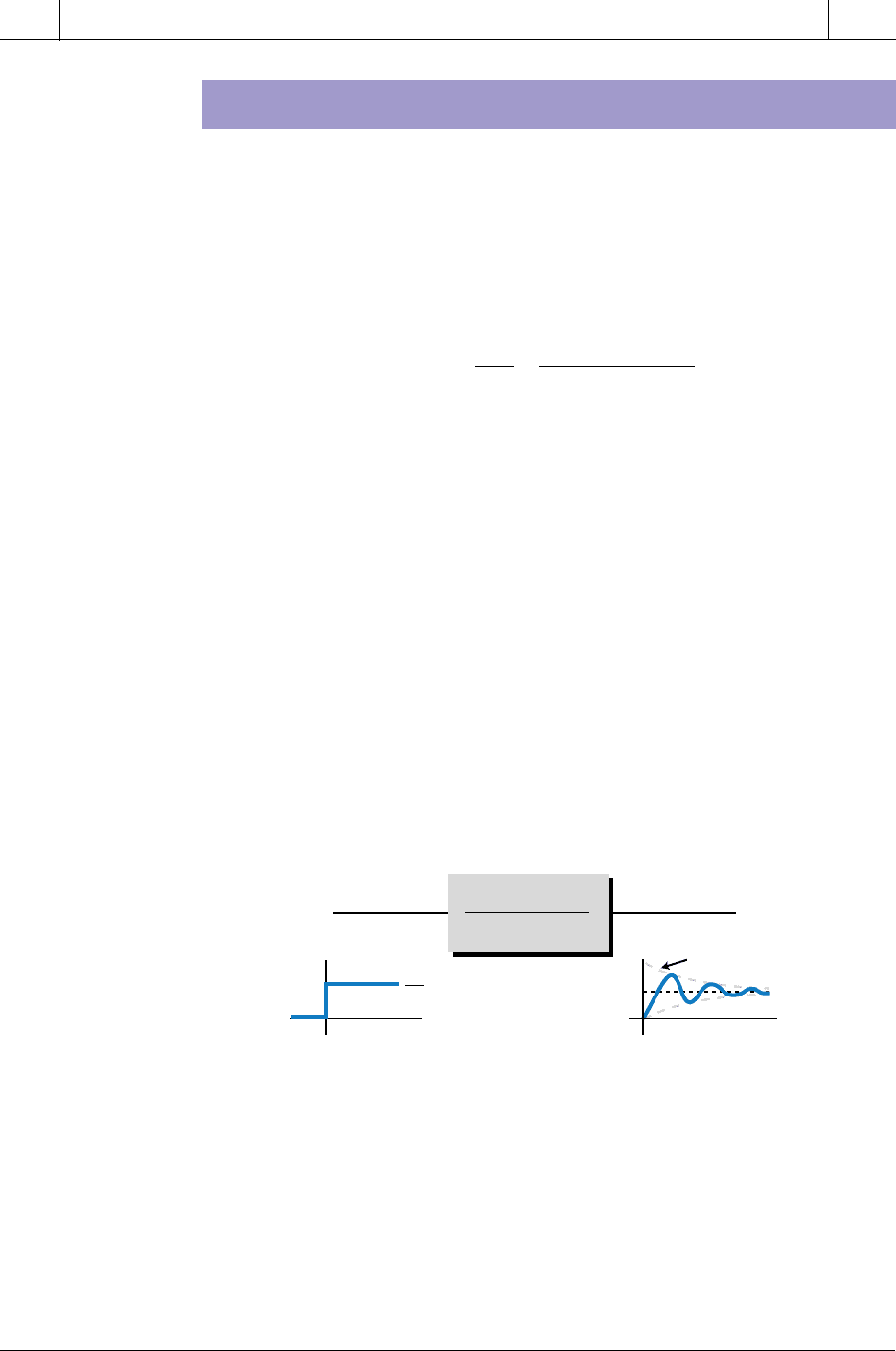
Figure 14-45. Second-order response to a step input.
SECOND-ORDER LAG RESPONSES
A second-order lag response exhibits oscillations that occur while the output
signal is settling into its final steady-state value. This type of response is
caused by a step change in the input or a disturbance in the process.
A second-order transfer function with lag is characterized by a second-order
differential equation that is represented in Laplace form as:
Hp
A
ss
s
n
nn
()
==
++
()
Out
In
ω
ζω ω
2
22
2
where:
A
n
=
=
the gain
the resonant, or natural, frequency of oscillation in radians/second
= the damping coefficient
ω
ζ
Figure 14-45 illustrates this second-order, oscillating response to a step
input. The frequency term ω
n
is the factor that determines how quickly the
response oscillates above and below the desired outcome. The damping
coefficient ζ is the factor that suppresses the oscillation over time, so that the
response finally levels off at the desired outcome value. The complete
numerator term Aω
n
2
represents the system gain (K
sys
), which specifies the
total amplitude of the response signal given its frequency.
In Out
Hp
A
ω
n
2
s
2
+ 2ζω
n
s
+ ω
n
2
A
1
s
A
1
A
1
A
2
Damping
e
–ζω
n
t
The amplitude of the oscillation of a second-order response dies off exponen
-
tially due to the damping of the factor
e
n
t−ζω
, which is part of the inverse
Laplace transform representation (time domain) of the system. If the damping
coefficient (ζ) is equal to 0, then the term
e
n
t−ζω
will be 1 and the response will
oscillate indefinitely in a sinusoidal manner at a frequency of ω
n,
instead of
leveling out. Thus, the damping coefficient determines the shape of the
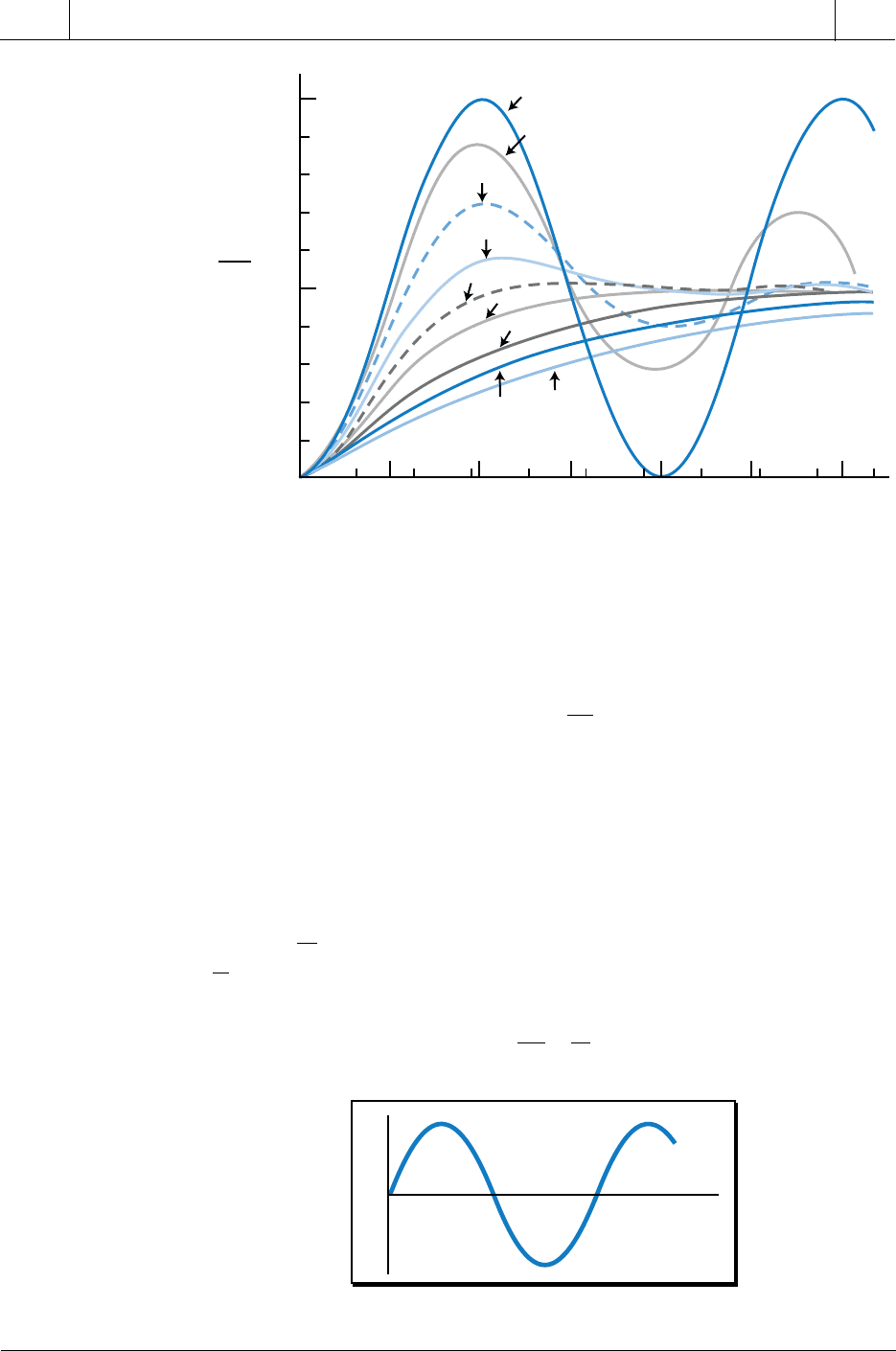
response (see Figure 14-46).
652
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
Figure 14-46. Damping coefficient effect on the oscillation of a second-order response.
Figure 14-47. Sinusoidal response of a second-order system around the set point.
Unlike a first-order system, a second-order system has two lag times (τ
1
and
τ
2
), which are related to the frequency of oscillation (ω
n
). These two lag times
combine to create a system second-order time constant τ
sys
, which is equal to:
τ
ω
sys
=
1
n
As used in Laplace and time domain second-order response equations, the
term ω
n
represents frequency. This frequency is expressed in radians per
second. However, this frequency can also be expressed in degrees. A
second-order response is a sinusoidal response, meaning that it fluctuates
above and below the final outcome (set point) value once every 2π periods
(see Figure 14-47). Therefore, the response period is characterized by the
equation
2π
ω
n
(see Figure 14-48). In degrees, this same period is expressed as
1
f
n
, where f
n
is the frequency in hertz. Therefore:
21
π
ω
nn
f
=
2.0
1.8
1.6
1.4
1.2
1.0
0.8
0.6
0.4
0.2
0
0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0 10.0
π/2 π 3π/2 5π/22π 3π
ζ = 0
ζ = 0.2
ζ = 0.5
ζ = 1.0
ζ = 4
ζ = 5
ζ = 1.5
ζ = 3
ζ = 2
ω
n
t
(in radians)
Out
In
2ππ0
653
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
2π
ω
n
1
f
n
or
Figure 14-48. Response period of a sinusoidal curve.
Solving for ω
n
yields:
ωπ
nn
f=2
So, the radian/sec frequency term ω
n
is equivalent to the degree frequency
term 2πf
n
.
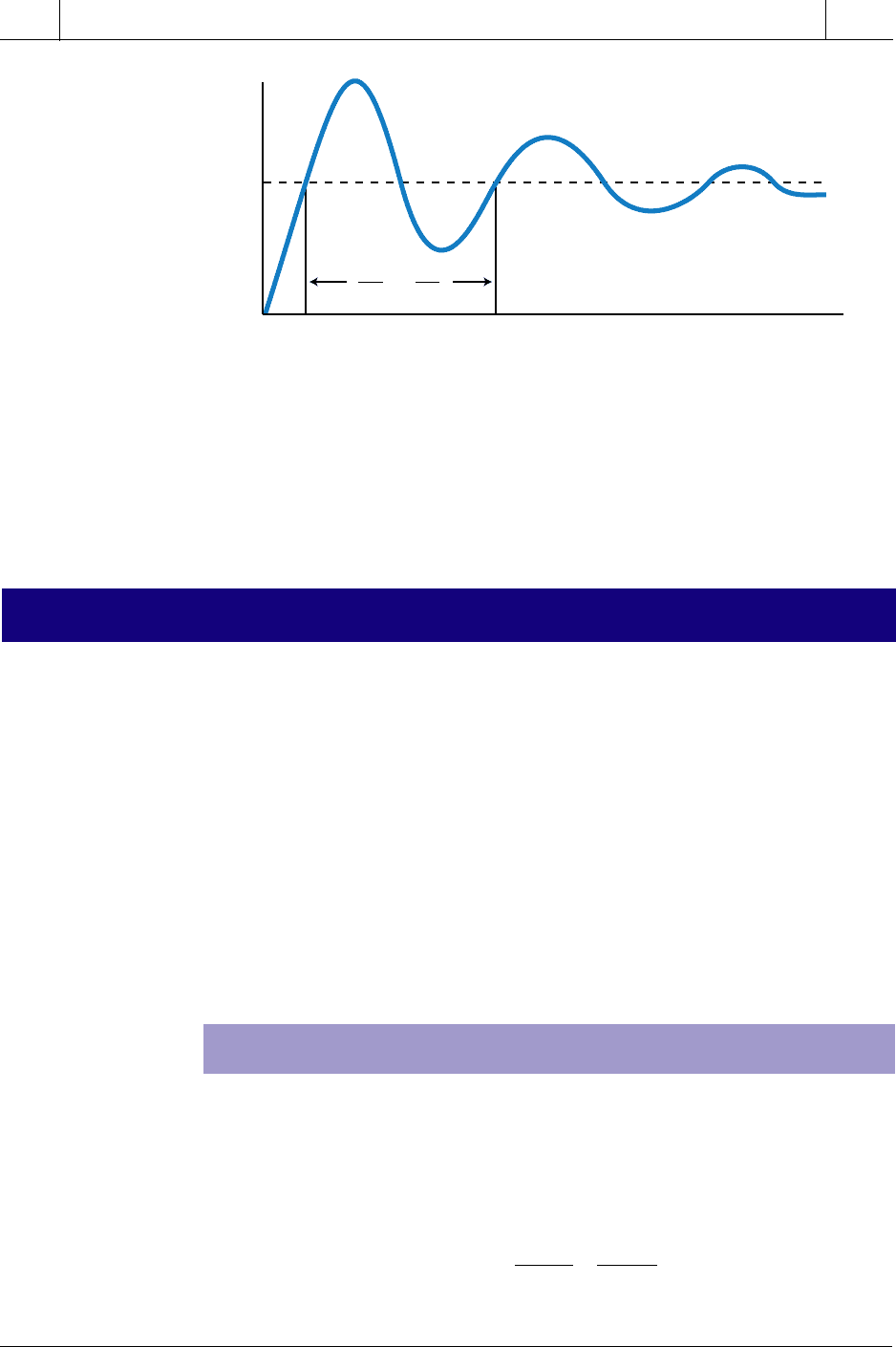
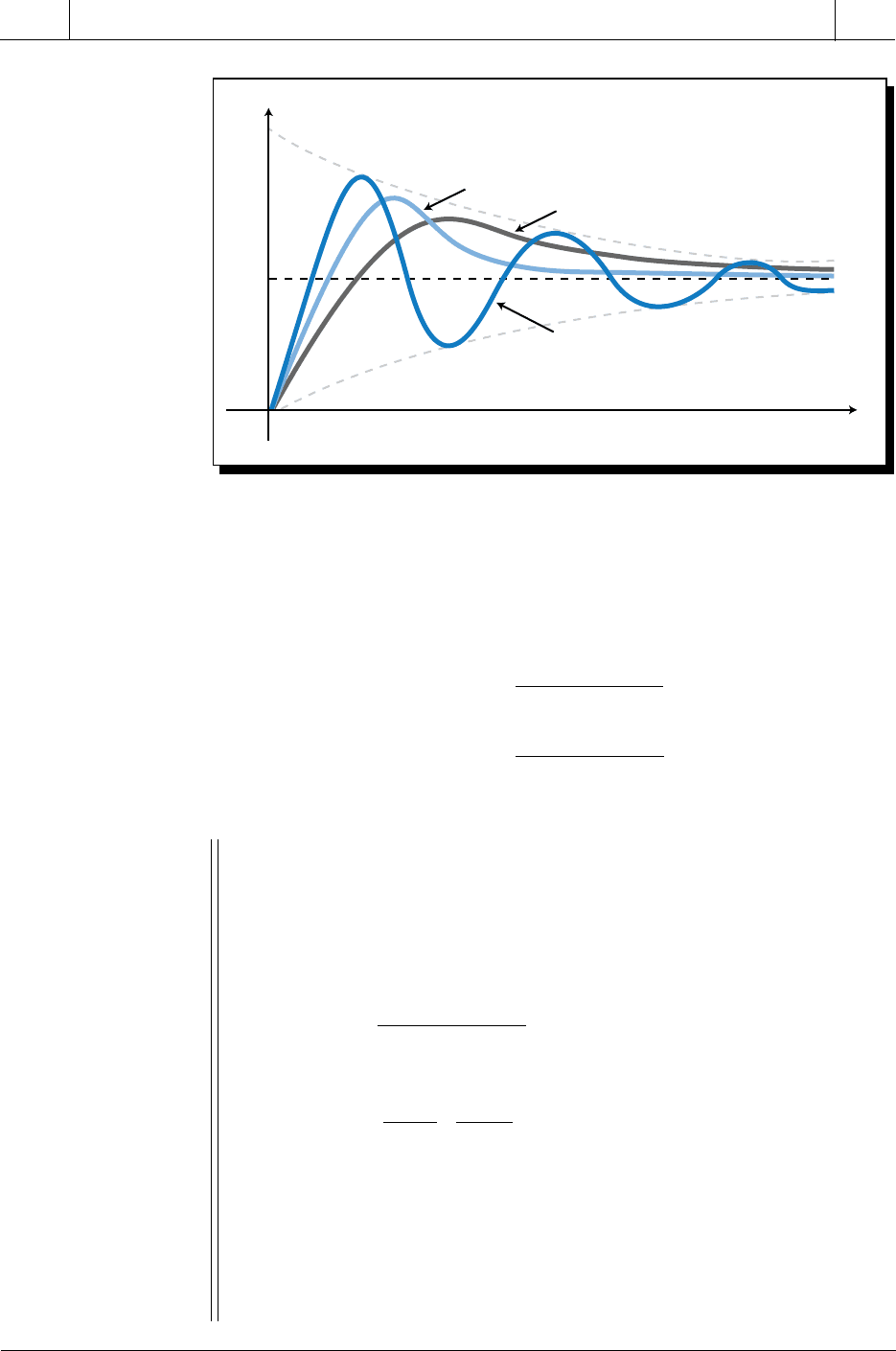
14-7 TYPES OF SECOND-ORDER RESPONSES
A second-order system can exhibit one of three types of responses:
• overdamped (ζ > 1)
• critically damped (ζ = 1)
• underdamped (ζ < 1)
These responses differ in how they reach the final steady-state value, or set
point, over time due to the value of their damping coefficients (see Figure 14-
49). An underdamped response oscillates around the set point because its time
domain transfer function contains the damping term
e
n
t−ζω
. Critically damped
and overdamped responses do not contain this term, so they overshoot the set
point and then settle back to it.
OVERDAMPED RESPONSES
An overdamped response is a second-order response with lag whose
damping coefficient (ζ) is greater than 1. By algebraically manipulating the
transfer function of a second-order system with lag (see Section 14-5), the
transfer function of an overdamped response can be expressed as:
Hp
A
s
A
s
s()
=
+
+
1
1
2
2
11
ττ
654
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
EXAMPLE 14-5
For an overdamped system (
ζ > 1), solve for (a)
K
sys
, (b) ω
n
, (c) τ
sys
,
and (d) ζ using the transfer functions for a second-order response and
an overdamped response.
Hp
A
ss
s
n
nn
()
=
++
(
)
ω
ζω ω
2
22
2
(Second-order transfer function)
Hp
A
s
A
s
s
()
=
+
+
1
1
2
2
11ττ
(Overdamped response)
S
OLUTION
Multiplying the terms in the overdamped transfer function yields the
equation:
Figure 14-49. Overdamped, critically damped, and underdamped responses.
In this equation, which is a function of two first-order systems (i.e., two time
lags), the terms A
1
and A
2
represent the gains. By substituting the term K
OD
for
the total overdamped system gain A
1
A
2
, this function can be simplified to:
Hp
AA
ss
K
ss
s
OD
()
=
+
()
+
()
=
++
12
12
12
11
11
ττ
ττ
()()
SP
Underdamped (ζ < 1)
Overdamped (ζ > 1)
Critically damped (ζ = 1)
t

655
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
sys
K
678
2
ζω
n
123
ω
n
2
{
Hp
AA
ss
AA
ss
s
()
()()
()
=
++
=
++ +
[]
12
12
12
12
2
12
11
1
ττ
ττ τ τ
Dividing by the term τ
1
τ
2
generates the following equation, which has
a denominator in the form of a second-order lag transfer function:
Hp
ss
s
AA
()
()
=
(
)
++
(
)
+
12
12
12
12 12
2
1
ττ
ττ
ττ ττ
Therefore, this equation is equal to the second-order lag equation:
Hp
A
ss
s
n
nn
()
=
++
(
)
ω
ζω ω
2
22
2
because the denominator of the polynomial can be separated into two
real factors, where τ
1
and τ
2
are the two time constants. Thus, the
relationship of the terms in these two equations is:
Hp
ss
s
AA
()
()
=
(
)
++
(
)
+
12
12
12
12 12
2
1
ττ
ττ
ττ ττ
(a) Knowing that the term
K
OD
is equal to the overdamped system gain
A
1
A
2
, the term
K
sys
for an overdamped system is:
KA
AA K
n
OD
sys
===
ω
ττ ττ
2
12
12 12
(b) For an overdamped system, ω
n
2
is equal to:
ω
ττ
n
2
12
1
=
Solving for ω
n
generates:
ω
ττ
ω
ττ
ττ
n
n
2
12
12
12
1
1
1
=
=
=
656
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
(c) Earlier, we explained that τ
sys
is equal to 1 over the frequency ω
n
.
Using the information from part (b), τ
sys
for an overdamped system is:
τ
ω
ττ
ττ
sys
=
=
(
)
=
1
1
1
12
12
n
(d) The damping coefficient terms for a second-order system with lag
and an overdamped system relate as follows:
2
12
12
ζω
ττ
ττ
n
=
+
(
)
Solving for ζ yields:
2
2
2
2
12
12
12
12
12
12
12
12
12
1
2
12
12
12
ζω
ττ
ττ
ζ
ττ
ττ ω
ττ
ττ
ττ
ττ
ττ
ττ
ττ
ττ
n
n
=
+
(
)
=
+
(
)
(
)
(
)
=
+
(
)
(
)
(
)
(
)
=
+
(
)
(
)
=
+
(
)
(
)
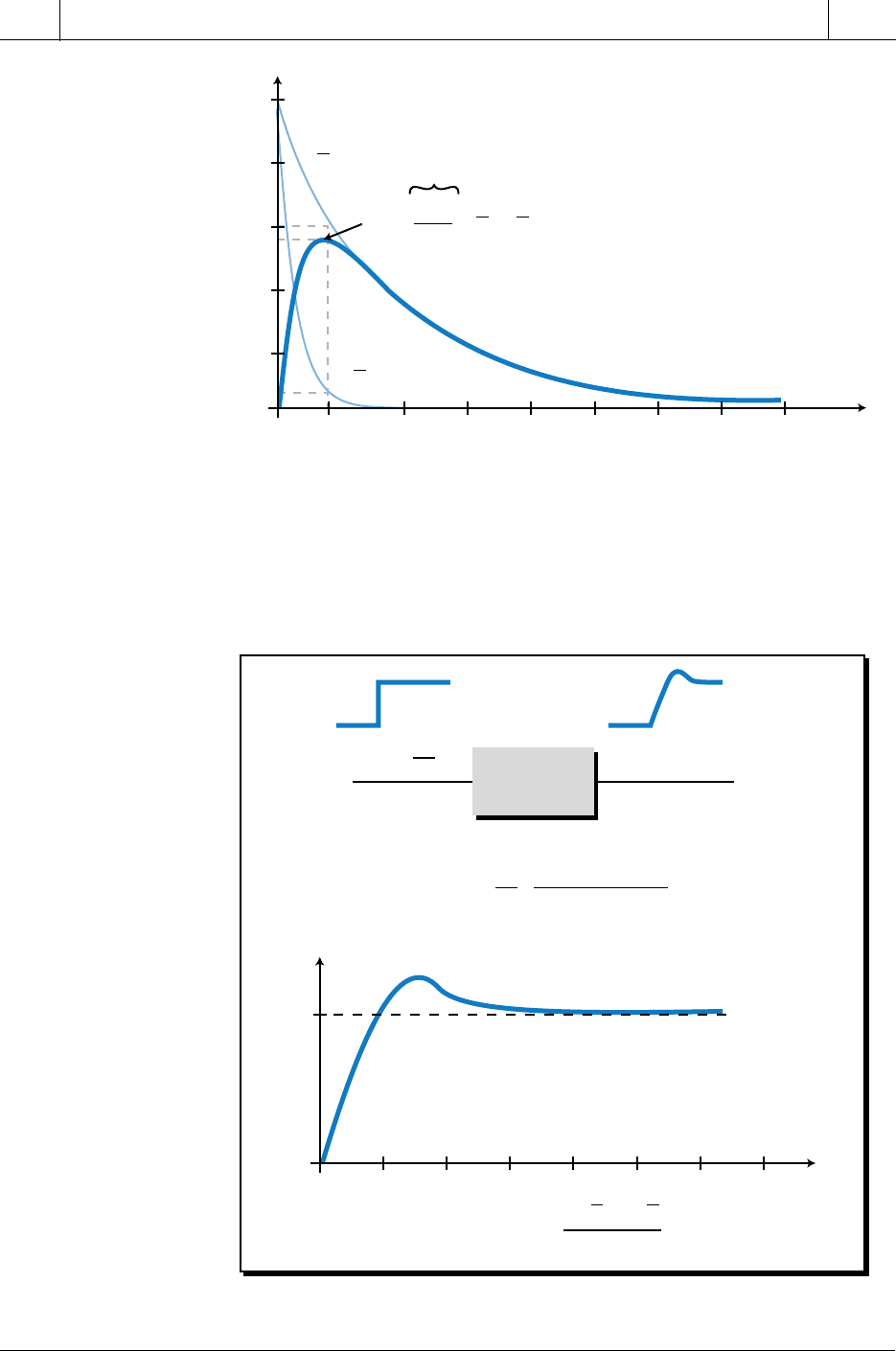
An overdamped second-order transfer function in real time (the time domain)
is described by the inverse Laplace transform (see Table 14-2):
H
K
ee
t
OD
tt
()
=
−
−
−−
ττ
ττ
12
12
This indicates two exponential decaying responses—one at a rate of τ
1
and
the other at the rate of τ
2
. Figure 14-50 illustrates the form of these two
exponential responses, along with the response of H
(t)
, which is a function of
a combination of these two responses. Note that, as indicated in the time
domain transfer function term (
ee
tt−−
−
ττ
12
), the curve of H
(t)
is equal to the curve
of the τ
1
response minus the curve of the τ
2
response.
657
CHAPTER
14
Process Responses
and Transfer Functions
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Figure 14-50. Real-time transfer function of an overdamped second-order process.
t
H
(
t
)
= (
e
–
e
)
Gain
K
OD
=
A
H
A
τ
1
– τ
2
3
2.75
0.25
e
e
τ
1
–t
τ
2
–t
τ
1
–t
τ
2
–t
Figure 14-51 illustrates a second-order system response to a step input with
amplitude B. As shown in this figure, the output of the time domain transfer
function in response to a step input is similar in form to the second-order
response curve shown in Figure 14-50. The overdamped response may also
follow the shape of a first-order system response curve if one of the time
Figure 14-51. Second-order response to a step input.
t
BK
OD
Out
(
t
)
In
(
s
)
= Out
(
s
)
H
(
s
)
B
s
B
s
K
OD
(τ
1
s
+ 1)(τ
2
s
+ 1)
Out
(
s
)
= In
(
s
)
H
(
s
)
Out
(
s
)
=
Out
(
t
)
=
BK
OD
1 +
()
τ
1
e
– τ
1
e
τ
2
– τ
1
(
(
τ
1
–t
τ
2
–t
658
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
14
Process Responses
and Transfer Functions
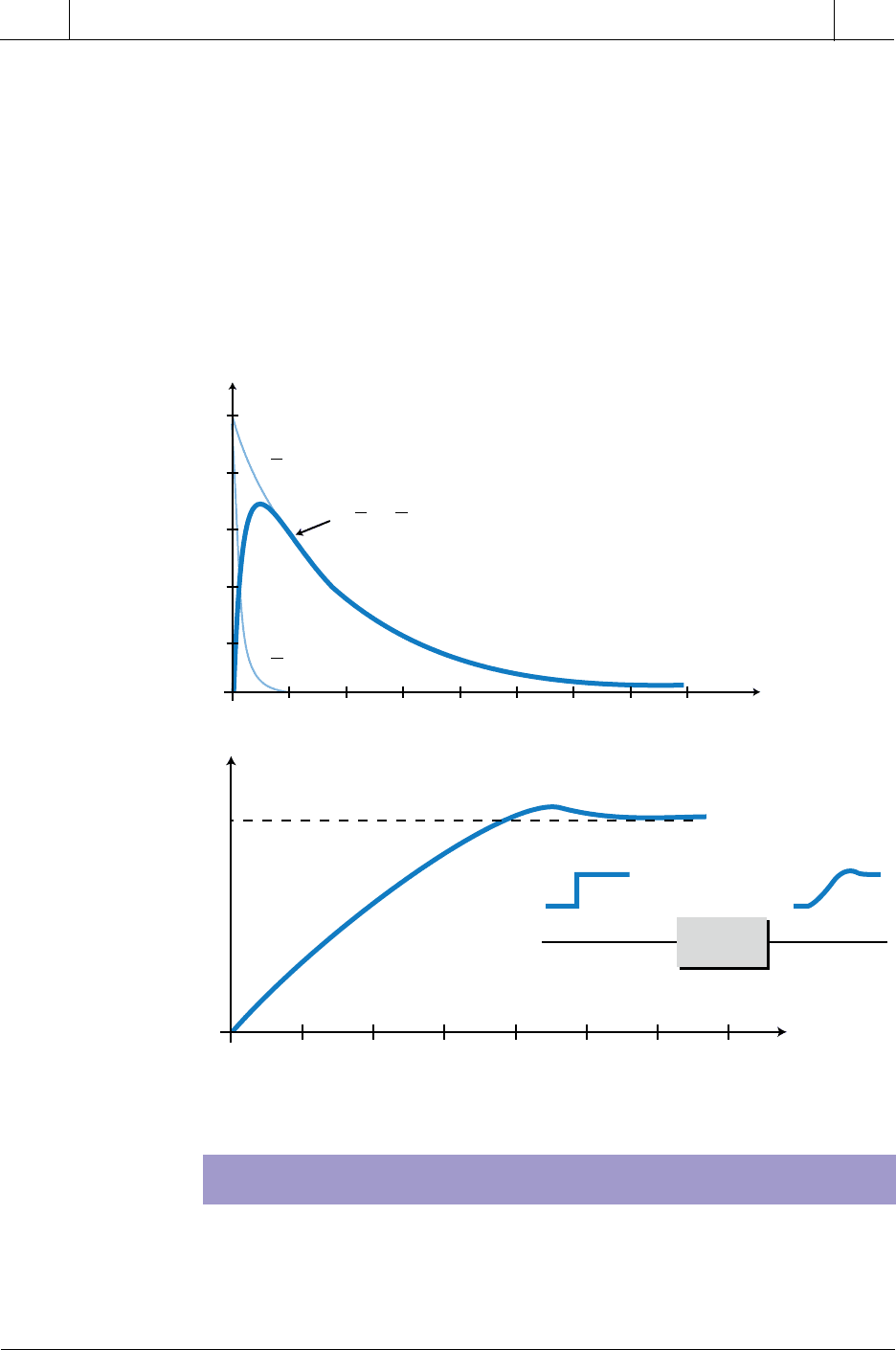
Figure 14-52. A heavily damped response.
constants is significantly longer than the other (i.e., τ
1
>> τ
2
). Figure 14-52
illustrates a case like this, where one of the exponential components (τ
2
) dies
out much more rapidly than the other (τ
1
). Thus, the response to the unit step
is heavily damped, causing a sluggish response similar to a first-order one.
The system response is heavily damped because the value of ζ in this system
becomes large (see the value of ζ in Example 14-4). Two first-order systems
with different time lags, which are connected in series (or cascaded), will
produce this type of overdamped second-order response (see Figure 14-53).
In a cascaded system, the output of one part of the system depends on the input
to another part of the system.
t
(
e
–
e
)
t
1
Out
(
s
)
H
(
s
)
Second-Order
System
τ
1
>> τ
2
H
(
t
)
τ
1
>> τ
2
Response to a unit step
e
e
Process Transfer Function [
Hp
(t)
]
τ
1
–t
τ
1
–t
τ
2
–t
τ
2
–t
CRITICALLY DAMPED RESPONSES
Critically damped responses, which are second-order responses where ζ =
1, are the result of second-order transfer functions where τ
1
= τ
2
. Therefore,
the transfer function for this type of response is (τ = τ
1
= τ
2
):
