Bryan L. Programmable controllers. Theory and implementation
Подождите немного. Документ загружается.

559
CHAPTER
13
Data Measurements
and Transducers
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Table 13-1. Measurement error types and their causes.
srorrEssorGsrorrEmetsySsrorrEmodnaR
elbissoP
sesuaC
elacstcerrocninagnisusgnidaeR•
sgnidaertnemurtsnieslaF•
tnemtsujdaorezfognittesreporpmI•
alumrofgnorwehtfoesU•
atadfognidrocertcaxenI•
sgnittestnemurtsnitcerrocnI•
ylreporpdetarbilactontnemurtsnI•
seitiraenilnonrofdetnuoccanU•
straptuo-nroW•
reporpmioteudrewopfossoL•
noitacilppa
,.g.e(tnemnorivnenisegnahC•
)erutarepmetdnaerusserp
•ehtnidesuslairetamfonoitairaV
enilssecorp
•enilroyevnocninoitarbiV
ecnabrutsidlacisyhprehtoynA•
noitciderP nwardebnacnoitciderpoN•foesohtotsgnidaererapmoC•
snoitaluclacdradnats
reteD•tahtosrorremetsysehtenim
aderusaemebnacrorreevitalumuc
detcepxedna
sisylanalacitsitatsfonoitacilppA•
atadgnitcellocybdeniatbo
ronoitneverP
noitcudeR
tcerrocotnoitnettaeromyaP•
syalpsid
ehtekatsnosreptnereffidevaH•
sgnidaeremas
namorfsgnidaerelpitlumekaT•
tnemurtsni
tnemurtsnifoerawaeB•
seitilibapac
ylralugerstnemurtsnietarbilaC•
foecnanetniamralugerezisahpmE•
stnemurtsnidnayrenihcam
ehtfoycnetsisnocehtrotinoM•
euqinhcet
ebdluohsstnemtsujdalacisyhP•
ehtdnastnemurtsniotedam
nacyehttahtos,enilssecorp
secnabrutsiddnatshtiw

560
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
13
Data Measurements
and Transducers
13-2 INTERPRETING ERRORS IN MEASUREMENTS
The discovery of errors is invaluable when controlling a machine or process
because error information helps the user improve the system. Errors can be
discovered in anticipation of the outcome (error prediction) or after a product
is made (error detection). Error prediction is more useful than error detection,
but it is harder to implement. Detection of an error after a product is made is
fairly easy, since the final product can be checked against a reference model
that matches all specifications. Although error prediction is much more
useful, error detection is better than not discovering the error at all. For
example, it is better to stop production of a machined piece because it has
been found that the piece does not meet the customer’s specifications than to
ship a bad product to the customer.
Once an error is detected, it can be interpreted using statistical analysis. This
type of statistical data analysis is, in fact, part of the foundation of artificial
intelligence systems. These systems continuously collect data about a
process and adjust production parameters accordingly. They then store their
data measurements in a global database for use in later statistical analysis
(see Chapter 16 for more about artificial intelligence systems).
In automated control systems, the controlling system and the process itself
usually generate system errors. Several events, composed of a mix of several
process errors, may combine to form a compounded system error. Likewise,
guarantee errors, caused by errors in raw materials or supplies, may also
generate system errors. Because their cause can be found, system errors can
be predicted and corrected.
Unknown events that occur during the process create random errors. There-
fore, unlike system errors, random errors can only be detected and corrected,
not predicted. Most of the time, the user must employ statistical analysis to
detect and remedy these errors.
INTERPRETING COMBINED ERRORS
Combined errors are errors caused by the interaction of two or more indepen-
dent variables, each one causing a different problem. The system propagates
the interaction of these variables; therefore, combined errors are also called
propagation errors. By calculating statistical data about the sample before
propagation and knowing the average and standard deviation requirements
for the final product, the user can predict the outcome of the final product
and make corrections for propagation errors throughout the process.
The value of an outcome formed by several variables (e.g., materials going
into a batching process) is directly related to the average value of each
variable. For instance, if a batching process uses two ingredients, A and B,
561
CHAPTER
13
Data Measurements
and Transducers
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
and their average weights are
AB and
, then the final weight of a mix
containing both materials would be
AB+
. This outcome is the addition of
both
AB and
because the operation to be performed is a blending, which
implies that the quantities are added. Thus, the final outcome is directly
related to the equation that governs the process being performed. In real life,
the actual equation of a process is very hard to obtain; it is usually only
approximated.
Standard deviation specifies how each sample value relates to the mean.
Accordingly, the standard deviation of an outcome product can predict how
the value of the final product will be spread out about its mean in relation to
each of its component variables. This information forecasts the variance of
the final product value. In the previous blending example, the average weight
outcome (W) is represented by:
WAB=+
where
AB and
are the average weights of the ingredient products. If the
distribution follows the normal (bell) curve, then:
• 68% of all samples lie within W ± 1σ
W
, or (
AB+
) ± 1σ
W
• 95% of all samples lie within W ± 2σ
W
, or (
AB+
) ± 2σ
W
• 99% or all samples lie within W ± 3σ
W
, or (
AB+
) ± 3σ
W
where σ
W
is the standard deviation of the final product.
However, to find the actual standard deviation, we must define the relation
-
ship between ingredients A and B and σ
W
. To obtain an equation that allows
two or more input variables, let’s define the function K as the equation
governing the final product and/or process. After numerous sample observa-
tions (n), the final product formula (K
n
) will be a function of the amount of
ingredients A and B added during the sample observations—A
n
and B
n
. That
is:
KKAB
nnn
=(,)
We can conclude that the most likely value for the function (the average
value) is:
KKAB
n
=(,)
where the final outcome is a function of the two averages. We can define any
deviation of a sample observation from the mean as ∆K
n
, which is expressed

562
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
13
Data Measurements
and Transducers
EXAMPLE 13-1
A manufacturing plant produces sphere-shaped pellets. These pel-
lets are heated for a period of time to make specific changes in the
sphere size. After numerous observations, quality control has deter-
mined that the radius (
r
) has a mean of 1.0 inch and a standard
deviation (σ
r
) of 0.0008 inches. The pellet material weight (
W)
has a
mean value of 0.15 lbs/in
3
and a standard deviation (σ
W
) of 0.00082
lbs/in
3
.
(a) Find the probable sphere weight of the final product and its
standard deviation. (b) Make suggestions about how this information
could be used.
as:
∆
∆
KKKAB
KKABKAB
nn
nnn
=−
=−
(,)
(,) (,)
or
If the deviation from the mean is 0 (∆K
n
= 0), implying that the value of the
nth observation is the same as the mean, then we would have:
KAB KAB
nn
(,) (,)=
Based on differential calculus theory, we can transform the ∆K
n
term into
partial derivatives as:
∆∆∆K
K
A
A
K
B
B
nnn
=+
∂
∂
∂
∂
By taking the average value of the sum of the squares and performing the
square root of the right-hand term, we have:
σ
∂
∂
σ
∂
∂
σ
KAB
K
A
K
B
=
+
2
2
2
2
where σ
K
is the standard deviation of the final outcome and σ
A
and σ
B
are the
standard deviations of the independent variables A and B. The other terms are
the partial derivatives of the function. This equation indicates that an
approximate standard deviation of a function (product) can be predicted by
knowing the standard deviations of the independent variables and the func-
tion of the process itself. The following example illustrates the use of this
function.

563
CHAPTER
13
Data Measurements
and Transducers
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
SOLUTION
(a) The total weight (
W
t
) of the sphere can be calculated as volume
times weight (
V
x
W
):
Vr
WVW
rW
t
=
=
=
4
3
3
4
3
3
π
π
Therefore, the final total weight of the product under normal process
conditions is:
W
t
=
=
4
3
3 1416 1 0 0 15
0 628
3
(. )(.)(. )
. lbs
The standard deviation is calculated using the formula:
σ
∂
∂
σ
∂
∂
σ
πσ πσ
W
t
W
t
r
Wr
t
W
W
W
r
rWr
=
+
=
(
)
(
)
+
(
)
(
)
=×+×
=
−−
2
22
3
2
2
2
2
2
77
4
3
4
17 545 6 7 10 3 553 6 4 10
0 003746
( . )( . ) ( . )( . )
. lbs
(b) The previous calculations show that, based on the samples
obtained for the average radius and average weight of the produced
part, the standard deviation of the finished product can be estimated
at 0.003746 lbs. If this value is within the range specified by quality
control, the product will be acceptable. On the other hand, if the value
for average final weight fluctuates greatly, producing an unaccept-
able standard deviation value, the process must be altered so that the
part meets quality control specifications. These process alterations
could include raising or lowering the heat to control the radius of the
part (by expansion), thus shaping the sphere so that its weight is
within the desired standard deviation range. This process adjustment
would, however, require a definition of the amount of heat needed to
alter the shape and size of the pellets. In order to make this kind of
process adjustment, the system must be capable of measuring
samples during the manufacturing process via transducers and other
measuring equipment.

564
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
13
Data Measurements
and Transducers
EXAMPLE 13-2
An electric heater with a current control system has a resistance value
of 150 ohms. The resistor has a guarantee deviation of ±0.15% of total
resistance. The current, which is controlled by a PLC’s analog output,
has a ±0.1% guarantee limit at 4.5 amps. Find the nominal power at
the heater and the error (deviation from the true mean) as guaranteed
by the limits.
S
OLUTION
The equation that describes power dissipation is:
PIR
=
2
where:
P
I
R
=
=
=
the power dissipation
the current
the resistance
Therefore, the nominal power calculation for the heater is:
P
=
=
(.)( )
.
4 5 150
3037 5
2
watts
The guarantee limits of the component are:
INTERPRETING GUARANTEE ERRORS
Guarantee errors are known values that state that a product or material’s
specifications will be within a specified arithmetic deviation from the mean.
For example, if a supplier specifies that a metal part used in an assembly line
has a length of 26 centimeters with a guarantee deviation (error) of less than
0.1%, then the length of its supplied parts is within a range of 26 cm ± 0.026
cm. Moreover, if the manufacturer specifies a ±3σ standard deviation, then
99% of the parts will be within ±0.026 cm of the mean.
To anticipate the possible value (outcome) of a process using guarantee
limits, the arithmetic worst-case scenario must be calculated. The following
example illustrates how two variables can be manipulated according to their
guarantee values to obtain the process outcome’s worst-case condition for
error tolerance.

565
CHAPTER
13
Data Measurements
and Transducers
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
I
R
=±
=±
=±
=±
45
150
.
amps 0.1%
4.5 0.0045 amps
ohms 0.15%
150 0.225 ohms
The variations in power, ∆
P
I
and ∆
P
R
(power variations due to current
and resistance, respectively), caused by each of the guarantee error
limits are:
∆∆∆
∆∆∆
P
P
I
IIRI
P
P
R
RIR
I
R
==
=±
=±
==
=±
=±
∂
∂
∂
∂
2
2 4 5 150 0 0045
6 075
45 0225
4 556
2
2
( . )( )( . )
.
(.)( . )
.
watts
watts
Adding these variation values to the nominal power value yields the
expected worst-case value:
PP P P
IR
=±±
=±±
=±
=±
nominal
watts
3037.5 10.631watts
watts
∆∆
3037 5 6 075 4 556
3037 5 0 35
.. .
..%
Thus, the variation in outcome power based on guarantee variable
errors is 0.35% of the total power.
13-3 TRANSDUCER MEASUREMENTS
This section deals primarily with two measuring techniques that are used to
implement transducer circuits. These techniques involve the use of bridge
circuits and linear variable differential transformer (LVDT) mechanisms.
For example, to detect pressure and changes in pressure, you can use a strain
gauge, which is based on the bridge circuit technique, or a Bourdon tube,
which is based on the LVDT mechanism technique. A knowledge of how
these transducer measurement circuits work will give you a better perspec-
tive of not only how they are used, but also where functional errors may occur
when measurement problems arise.
566
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
13
Data Measurements
and Transducers
BRIDGE CIRCUIT TECHNIQUES
Bridge circuits use resistive elements to sense measurement changes.
Depending on how the circuit is configured, the bridge will change the
voltage or current of its output in proportion to changes in its resistive
measurement element. This resistance change generally creates a bridge
imbalance. Under normal (balanced) operation of a bridge circuit, the current
that passes through one section of a current-sensitive bridge is the same as
that in the other section (or in a voltage-sensitive bridge, the voltage
differential between the two sections is zero). An imbalance occurs when
the resistance of one element changes, thus creating a current or voltage offset
that is proportional to the resistance change. The bridge circuit utilizes this
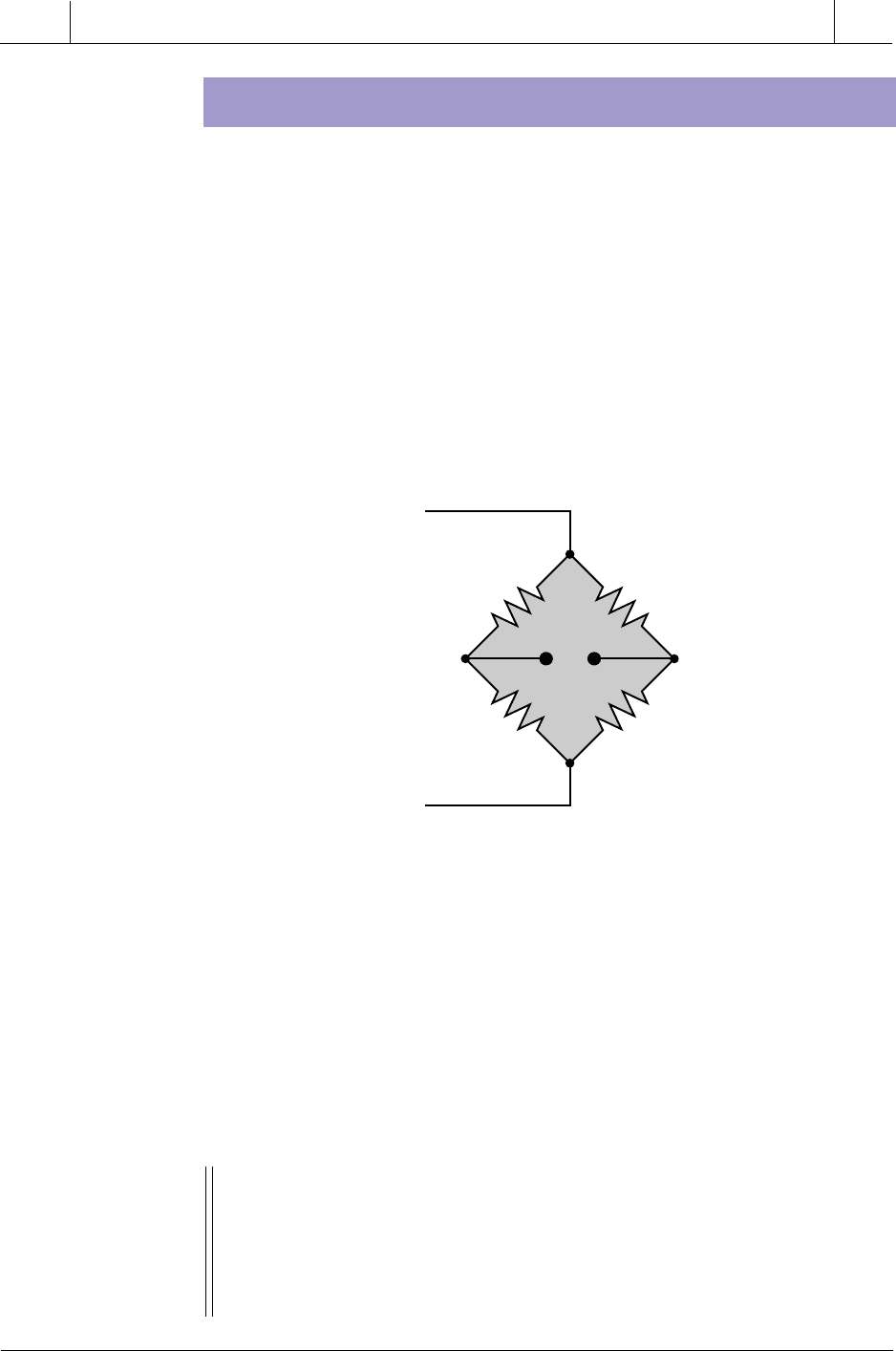
offset measurement to determine the value of the measured variable. Figure
13-3 shows a bridge circuit.
Figure 13-3. Simple bridge circuit.
Voltage-Sensitive Bridge. A voltage-sensitive bridge senses a voltage
differential at the output of the bridge that is proportional to the resistance
change in the bridge. Figure 13-4 illustrates a voltage-sensitive bridge, where
D is the detector device and R
D
is its resistance. The value of R
D
for a voltage-
sensitive bridge is very high. This amount of resistance could be provided by
the input impedance of an amplifier module of a PLC. The following example
illustrates the relationship between the resistors in a voltage-sensitive bridge
circuit. Note that a change in the resistance of R
4
(the measuring element)
creates the bridge imbalance; the other resistors have fixed, known values.
EXAMPLE 13-3
For the voltage-sensitive circuit shown in Figure 13-4, find (a) the
equation that describes the voltage differential measurement
between point A and point B
and (b) the bridge resistance ratio when
the voltage differential is 0 (balanced state).
R
1
R
3
R
2
R
4
Output

567
CHAPTER
13
Data Measurements
and Transducers
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
SECTION
4
PLC Process
Applications
Figure 13-4. Voltage-sensitive bridge circuit.
SOLUTION
(a) Assuming that
R
D
= ∞ (i.e., it is very large) and the excitation voltage
impedance (
R
i
) equals 0, the voltages at points
V
A
and
V
B
are:
V
R
RR
V
V
R
RR
V
A
B
=
+
=
+
3
13
4
24
The voltage differential between points A
and B
is:
∆
VV V
V
R
RR
R
RR
V
RR RR
RRRR
AB
=−
=
+
−
+
=
−
++
3
13
4
24
23 14
1324
()()
(b) When the differential voltage (∆
V
) is 0,
V
A
equals
V
B
, so:
R
RR
V
R
RR
V
R
RR
R
RR
RR RR RR RR
RR RR
3
13
4
24
3
13
4
24
23 34 14 34
23 14
+
=
+
+
=
+
+=+
=
R
1
R
i
R
3
R
2
R
4
24 VDC
D
AB
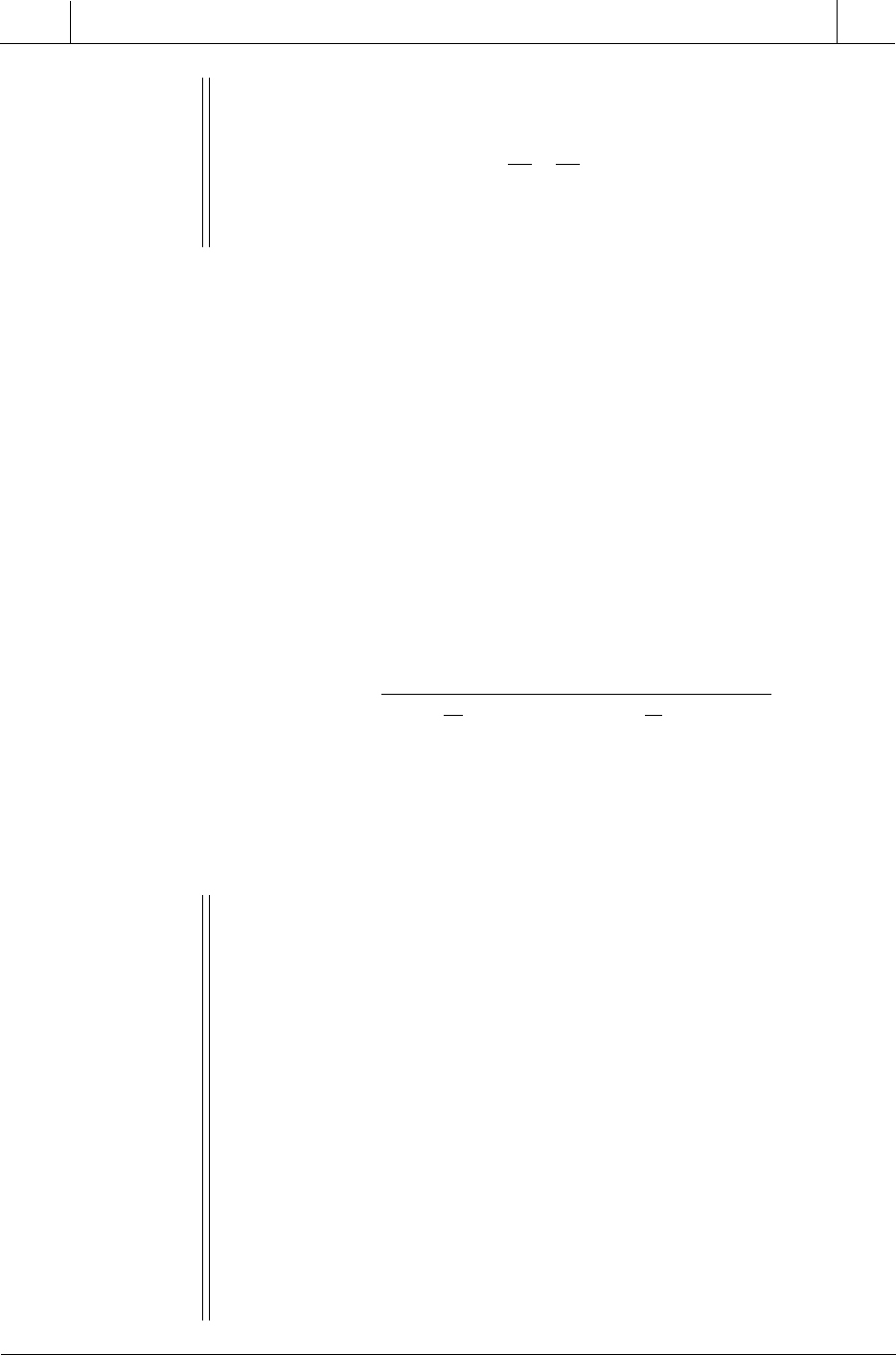
568
SECTION
4
PLC Process
Applications
Industrial Text & Video Company 1-800-752-8398
www.industrialtext.com
CHAPTER
13
Data Measurements
and Transducers
Therefore, the bridge resistance ratio is:
R
R
R
R
1
2
3
4
=
where
R
4
is the measuring resistance element.
Current-Sensitive Bridge. A current-sensitive bridge creates a current flow
change through the output of the bridge, that is, between point A and point B
(refer to Figure 13-4). The current flow is the result of a bridge imbalance
created by resistance changes in the measuring element. The other resistors
in the bridge have known, fixed values.
When current changes are being measured, the detecting device D has a very
low resistance R
D
, allowing current to flow from point A to B through the
detector. Typical devices that have very low impedance include galvanom-
eters and low-input impedance current amplifier interfaces (PLC modules).
The following equation describes the current that flows through a current-
sensitive bridge’s detector as a result of a bridge imbalance:
I
VR
RRRR RR
D
iBDB
R
R
R
R
=
+
()
++
[]
+
()
++
[]
4
24 34
11
2
11
3
The term R
4B
is the resistance value when the bridge is balanced. The
following example illustrates how this equation is used to obtain a current
proportional to the change in resistance.
EXAMPLE 13-4
A bridge circuit uses a thermistor with a nominal resistance of 10 Ω to
measure small changes in temperature (see Figure 13-5). An amplifier
input module, which has an input impedance of 300 Ω, measures small
changes in current. What is the current if a change in temperature
results in a 10% change in resistance?
S
OLUTION
The resistance of the thermistor (
R
4
)
changes 10% due to temperature
change, which translates into an
R
4
value of 11 Ω (10 Ω + 1 Ω). The term
∆
R
4
is the absolute value of the difference between
R
4
B
and the new
value of
R
4
due to the measurement change. Therefore, the difference
in thermistor resistance is calculated as:
