Brennen Ch.E. Fundamentals of Multiphase Flow

Подождите немного. Документ загружается.

oscillations is also predicted. Note that the quasistatic input resistance at

small frequencies remains positive throughout and therefore the system is

quasistatically stable for all steam ﬂow rates. Thus, chugging and conden-

sation oscillations are true, dynamic instabilities.

It is, however, important to observe that a linear stability analysis can-

not model the highly non-linear processes that occur during a chug and,

therefore, cannot provide information on the subject of most concern to the

practical engineer, namely the magnitudes of the pressure excursions and

the structural loads that result from these condensation instabilities. While

models have been developed in an attempt to make these predictions (see, for

example, Sargis et al. 1979) they are usually very speciﬁc to the particular

problem under investigation. Often, they must also resort to empirical infor-

mation on unknown factors such as the transient mixing and condensation

rates.

Finally, we note that instabilities that are similar to chugging have been

observed in other contexts. For example, when steam was injected into the

wake of a streamlined underwater body in order to explore underwater jet

propulsion, the ﬂow became very unstable (Kiceniuk 1952).

15.7 TRANSFER FUNCTIONS

15.7.1 Unsteady internal ﬂow methods

While the details are beyond the scope of this book, it is nevertheless of

value to conclude the present chapter with a brief survey of the transfer

function methods referred to in section 15.6. There are two basic approaches

to unsteady internal ﬂows, namely solution in the time domain or in the fre-

quency domain. The traditional time domain or water-hammer methods for

hydraulic systems can and should be used in many circumstances; these

are treated in depth elsewhere (for example, Streeter and Wylie 1967, 1974,

Amies et al. 1977). They have the great advantage that they can incorporate

the nonlinear convective inertial terms in the equations of ﬂuid ﬂow. They

are best suited to evaluating the transient response of ﬂows in long pipes

in which the equations of the ﬂow and the structure are well established.

However, they encounter great diﬃculties when either the geometry is com-

plex (for example inside a pump), or the ﬂuid is complex (for example in

a multiphase ﬂow). Under these circumstances, frequency domain methods

have distinct advantages, both analytically and experimentally. Speciﬁcally,

unsteady ﬂow experiments are most readily conducted by subjecting the

component or device to ﬂuctuations in the ﬂow over a range of frequen-

359

cies and measuring the ﬂuctuating quantities at inlet and discharge. The

main disadvantage of the frequency domain methods is that the nonlin-

ear convective inertial terms cannot readily be included and, consequently,

these methods are only accurate for small perturbations from the mean ﬂow.

While this permits evaluation of stability limits, it does not readily allow

the evaluation of the amplitude of large unstable motions. However, there

does exist a core of fundamental knowledge pertaining to frequency domain

methods (see for example, Pipes 1940, Paynter 1961, Brown 1967) that is

summarized in Brennen (1994). A good example of the application of these

methods is contained in Amies and Greene (1977).

15.7.2 Transfer functions

As in the quasistatic analyses described at the beginning of this chapter,

the ﬁrst step in the frequency domain approach is to identify all the ﬂow

variables that are needed to completely deﬁne the state of the ﬂow at each

of the nodes of the system. Typical ﬂow variables are the pressure, p,(or

total pressure, p

) the velocities of the phases or components, the volume

fractions, and so on. To simplify matters we count only those variables that

are not related by simple algebraic expressions. Thus we do not count both

the pressure and the density of a phase that behaves barotropically, nor

do we count the mixture density, ρ, and the void fraction, α,inamixture

of two incompressible ﬂuids. The minimum number of variables needed to

completely deﬁne the ﬂow at all of the nodes is called the order of the system

and will be denoted by N. Then the state of the ﬂow at any node, i,is

denoted by the vector of state variables, {q

},n=1, 2 → N. For example,

in a homogeneous ﬂow we could choose q

= p, q

= u, q

= α,tobethe

pressure, velocity and void fraction at the node i.

The next step in a frequency domain analysis is to express all the ﬂow

variables, {q

},n=1, 2 → N, as the sum of a mean component (denoted by

an overbar) and a ﬂuctuating component (denoted by a tilde) at a frequency,

ω. The complex ﬂuctuating component incorporates both the amplitude and

phase of the ﬂuctuation:

(s, t)} = {¯q

(s)} + Re

{˜q

(s, ω)}e

iωt

(15.5)

for n =1→ N where i is (−1)

and Re denotes the real part. For example

p(s, t)=¯p(s)+Re

˜p(s, ω)e

iωt

(15.6)

˙m(s, t)=

˙m(s)+Re

˙m(s, ω)e

iωt

(15.7)

360

α(s, t)= ¯α(s)+Re

˜α(s, ω)e

iωt

(15.8)

Since the perturbations are assumed linear (|˜u|¯u, |

˙m|

˙m, |˜q

|¯q

)

they can be readily superimposed, so a summation over many frequencies

is implied in the above expressions. In general, the perturbation quantities,

{˜q

}, will be functions of the mean ﬂow characteristics as well as position,

s, and frequency, ω.

The utilization of transfer functions in the context of ﬂuid systems owes

much to the pioneering work of Pipes (1940). The concept is the following.

If the quantities at inlet and discharge are denoted by subscripts m =1and

m = 2, respectively, then the transfer matrix, [T ], is deﬁned as

{˜q

} =[T ] {˜q

} (15.9)

It is a square matrix of order N . For example, for an order N = 2 system

in which the independent ﬂuctuating variables are chosen to be the total

pressure, ˜p

, and the mass ﬂow rate,

˙m, then a convenient transfer matrix



˜p

˙m









˜p

˙m



(15.10)

In general, the transfer matrix will be a function of the frequency, ω,ofthe

perturbations and the mean ﬂow conditions in the device. Given the transfer

functions for each component one can then synthesize transfer functions for

the entire system using a set of simple procedures described in detail in

Brennen (1994). This allows one to proceed to a determination of whether

or not a system is stable or unstable given the boundary conditions acting

upon it.

The transfer functions for many simple components are readily identiﬁed

(see Brennen 1994) and are frequently composed of impedances due to ﬂuid

friction and inertia (that primarily contribute to the real and imaginary

parts of T

respectively) and compliances due to ﬂuid and structural com-

pressibility (that primarily contribute to the imaginary part of T

). More

complex components or ﬂows have more complex transfer functions that can

often be determined only by experimental measurement. For example, the

dynamic response of pumps can be critical to the stability of many internal

ﬂow systems (Ohashi 1968, Greitzer 1981) and consequently the transfer

functions for pumps have been extensively explored (Fanelli 1972, Anderson

et al. 1971, Brennen and Acosta 1976). Under stable operating conditions

(see sections 15.3, 16.4.2) and in the absence of phase change, most pumps

can be modeled with resistance, compliance and inertance elements and they

361

are therefore dynamically passive. However, the situation can be quite dif-

ferent when phase change occurs. For example, cavitating pumps are now

known to have transfer functions that can cause instabilities in the hydraulic

system of which they are a part. Note that under cavitating conditions, the

instantaneous ﬂow rates at inlet and discharge will be diﬀerent because of

the rate of change of the total volume, V , of cavitation within the pump and

this leads to complex transfer functions that are described in more detail in

section 16.4.2. These characteristics of cavitating pumps give rise to a vari-

ety of important instabilities such as cavitation surge (see section 15.6.2) or

the Pogo instabilities of liquid-propelled rockets (Brennen 1994).

Much less is known about the transfer functions of other devices involv-

ing phase change, for example boiler tubes or vertical evaporators. As an

example of the transfer function method, in the next section we consider a

simple homogeneous multiphase ﬂow.

15.7.3 Uniform homogeneous ﬂow

As an example of a multiphase ﬂow that exhibits the solution structure

described in section 15.7.2, we shall explore the form of the solution for

the inviscid, frictionless ﬂow of a two component, gas and liquid mixture

in a straight, uniform pipe. The relative motion between the two compo-

nents is neglected so there is only one velocity, u(s, t). Surface tension is

also neglected so there is only one pressure, p(s, t). Moreover, the liquid

is assumed incompressible (ρ

constant) and the gas is assumed to behave

barotropically with p ∝ ρ

. Then the three equations governing the ﬂow are

the continuity equations for the liquid and for the gas and the momentum

equation for the mixture which are, respectively

∂

∂t

(1 − α)+

∂

∂s

[(1 − α)u] = 0 (15.11)

∂

∂t

(ρ

α)+

∂

∂s

(ρ

αu) = 0 (15.12)



∂u

∂t

+ u

∂u

∂s



= −

∂p

∂s

(15.13)

where ρ is the usual mixture density. Note that this is a system of order

N = 3 and the most convenient ﬂow variables are p, u and α.Theserelations

362

yield the following equations for the perturbations:

−iω˜α +

∂

∂s

[(1 − ¯α)˜u − ¯u˜α] = 0 (15.14)

iω¯ρ

˜α + iω¯α˜ρ

+¯ρ

¯α

∂˜u

∂s

+¯ρ

¯u

∂ ˜α

∂s

+¯α¯u

∂ ˜ρ

∂s

= 0 (15.15)

−

∂ ˜p

∂s

=¯ρ



iω˜u +¯u

∂˜u

∂s



(15.16)

where ˜ρ

=˜p¯ρ

/k¯p. Assuming the solution has the simple form







˜p

˜u

˜α













iκ

+ P

iκ

+ P

iκ

+ U

iκ

+ U

iκ

+ A

iκ

+ A

iκ







(15.17)

it follows from equations 15.14, 15.15 and 15.16 that

(1 − ¯α)U

=(ω + κ

¯u)A

(15.18)

(ω + κ

¯u)A

¯α

k¯p

(ω + κ

¯u)P

+¯ακ

= 0 (15.19)

¯ρ(ω + κ

¯u)U

+ κ

= 0 (15.20)

Eliminating A

, U

and P

leads to the dispersion relation

(ω + κ

¯u)



1 −

¯α¯ρ

k¯p

(ω + κ

¯u)



= 0 (15.21)

The solutions to this dispersion relation yield the following wavenumbers

and velocities, c

= −ω/κ

, for the perturbations:

= −ω/¯u which has a wave velocity, c

=¯u. This is a purely kinematic wave, a

concentration wave that from equations 15.18 and 15.20 has U

=0andP

so that there are no pressure or velocity ﬂuctuations associated with this type of

wave. In other, more complex ﬂows, kinematic waves may have some small pres-

sure and velocity perturbations associated with them and their velocity may not

exactly correspond with the mixture velocity but they are still called kinematic

waves if the major feature is the concentration perturbation.

,κ

= −ω/(¯u ± c)wherec is the sonic speed in the mixture, namely c =

(k ¯p/¯α ¯ρ)

. Consequently, these two modes have wave speeds c

=¯u ± c and

are the two acoustic waves traveling downstream and upstream respectively.

363

Finally, we list the solution in terms of three unknown, complex constants

, P

and A







˜p

˜u

˜α











0 e

iκ

0 −e

iκ

/¯ρc e

iκ

/¯ρc

iκ

−(1 − ¯α)e

iκ

/¯ρc

−(1 − ¯α)e

iκ

/¯ρc

















(15.22)

and the transfer function between two locations s = s

and s = s

follows by

eliminating the vector { A

} from the expressions 15.22 for the state

vectors at those two locations.

Transfer function methods for multiphase ﬂow are nowhere near as well

developed as they are for single phase ﬂows but, given the number and ubiq-

uity of instability problems in multiphase ﬂows (Ishii 1982), it is inevitable

that these methods will gradually develop into a tool that is useful in a wide

spectrum of applications.

364

KINEMATIC WAVES

16.1 INTRODUCTION

The one-dimensional theory of sedimentation was introduced in a classic

paper by Kynch (1952), and the methods he used have since been expanded

to cover a wide range of other multiphase ﬂows. In chapter 14 we introduced

the concept of drift ﬂux models and showed how these can be used to analyse

and understand a class of steady ﬂows in which the relative motion between

the phases is determined by external forces and the component properties.

The present chapter introduces the use of the drift ﬂux method to analyse

the formation, propagation and stability of concentration (or kinematic)

waves. For a survey of this material, the reader may wish to consult Wallis

(1969).

The general concept of a kinematic wave was ﬁrst introduced by Lighthill

and Whitham (1955) and the reader is referred to Whitham (1974) for a

rigorous treatment of the subject. Generically, kinematic waves occur when a

functional relation connects the ﬂuid density with the ﬂux of some physically

conserved quantity such as mass. In the present context a kinematic (or

concentration) wave is a gradient or discontinuity in the volume fraction,

α. We will refer to such gradients or discontinuities as local structure in the

ﬂow; only multiphase ﬂows with a constant and uniform volume fraction will

be devoid of such structure. Of course, in the absence of any relative motion

between the phases or components, the structure will simply be convected at

the common velocity in the mixture. Such ﬂows may still be non-trivial if the

changing density at some Eulerian location causes deformation of the ﬂow

boundaries and thereby creates a dynamic problem. But we shall not follow

that path here. Rather this chapter will examine, the velocity of propagation

of the structure when there is relative motion between the phases. Then,

inevitably, the structure will propagate at a velocity that does not necessarily

365

correspond to the velocity of either of the phases or components. Thus it is

a genuinely propagating wave. When the pressure gradients associated with

the wave are negligible and its velocity of propagation is governed by mass

conservation alone, we call the waves kinematic to help distinguish them

from the dynamic waves in which the primary gradient or discontinuity is

in the pressure rather than the volume fraction.

16.2 TWO-COMPONENT KINEMATIC WAVES

16.2.1 Basic analysis

Consider the most basic model of two-component pipe ﬂow (components A

and B) in which the relative motion is non-negligible. We shall assume a

pipe of uniform cross-section. In the absence of phase change the continuity

equations become

∂α

∂t

∂j

∂s

=0 ;

∂α

∂t

∂j

∂s

= 0 (16.1)

For convenience we set α = α

=1− α

. Then, using the standard notation

of equations 15.5 to 15.8, we expand α, j

and j

in terms of their mean

values (denoted by an overbar) and harmonic perturbations (denoted by the

tilde) at a frequency ω in the form used in expressions 15.5. The solution

for the mean ﬂow is simply

)

= 0 (16.2)

and therefore

j is a constant. Moreover, the following equations for the

perturbations emerge:

∂

∂s

+ iω ˜α =0 ;

∂

∂s

− iω˜α = 0 (16.3)

Now consider the additional information that is necessary in order to

determine the dispersion equation and therefore the diﬀerent modes of wave

propagation that can occur in this ﬂow. First, we note that

= αj + j

; j

=(1− α)j − j

(16.4)

and it is convenient to replace the variables, j

and j

,byj, the total

volumetric ﬂux, and j

, the drift ﬂux. Substituting these expressions into

equations 16.3, we obtain

∂

∂s

=0 ;

∂(

j ˜α +

)

∂s

+ iω ˜α = 0 (16.5)

366

Figure 16.1. Kinematic wave speeds and shock speeds in a drift ﬂux chart.

The ﬁrst of these yields a uniform and constant value of

j that corresponds

to a synchronous motion in which the entire length of the multiphase ﬂow

in the pipe is oscillating back and forth in unison. Such motion is not of

interest here and we shall assume for the purposes of the present analysis

that

j =0.

The second equation 16.5 has more interesting implications. It represents

the connection between the two remaining ﬂuctuating quantities,

and ˜α.

To proceed further it is therefore necessary to ﬁnd a second relation connect-

ing these same quantities. It now becomes clear that, from a mathematical

point of view, there is considerable simplicity in the the Drift Flux Model

(chapter 14), in which it is assumed that the relative motion is governed by a

simple algebraic relation connecting j

and α, We shall utilize that model

here and assume the existence of a known, functional relation, j

(α). Then

the second equation 16.5 can be written as



j +

dα



¯α



∂ ˜α

∂s

+ iω ˜α = 0 (16.6)

where dj

/dα is evaluated at α =¯α and is therefore a known function of

¯α. It follows that the dispersion relation yields a single wave type given by

the wavenumber, κ, and wave velocity, c,where

κ = −

j +

dα



¯α

and c =

j +

dα



¯α

(16.7)

This is called a kinematic wave since its primary characteristic is the

perturbation in the volume fraction and it travels at a velocity close to

367

the velocity of the components. Indeed, in the absence of relative motion

c →

j = u

= u

The expression 16.7 (and the later expression 16.14 for the kinematic shock

speed) reveal that the propagation speed of kinematic waves (and shocks)

relative to the total volumetric ﬂux, j, can be conveniently displayed in a

drift ﬂux chart as illustrated in ﬁgure 16.1. The kinematic wave speed at a

given volume fraction is the slope of the tangent to the drift ﬂux curve at

that point (plus j). This allows a graphical and comparative display of wave

speeds that, as we shall demonstrate, is very convenient in ﬂows that can

be modeled using the drift ﬂux methodology.

16.2.2 Kinematic wave speed at ﬂooding

In section 14.3.1 (and ﬁgure 14.2) we identiﬁed the phenomenon of ﬂooding

and drew the analogies to choking in gas dynamics and open-channel ﬂow.

Note that in these analogies, the choked ﬂow is independent of conditions

downstream because signals (small amplitude waves) cannot travel upstream

through the choked ﬂow since the ﬂuid velocity there is equal to the small

amplitude wave propagation speed relative to the ﬂuid. Hence in the lab-

oratory frame, the upstream traveling wave speed is zero. The same holds

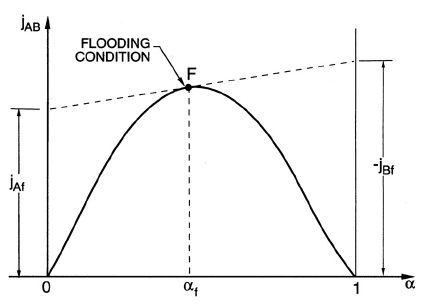
true in a ﬂooded ﬂow as illustrated in ﬁgure 16.2 which depicts ﬂooding at

avolumefractionofα

and volume ﬂuxes, j

and j

. From the geometry

Figure 16.2. Conditions of ﬂooding at a volume fraction of α

and volume

ﬂuxes j

and j

368