Brennen Ch.E. Fundamentals of Multiphase Flow

Подождите немного. Документ загружается.

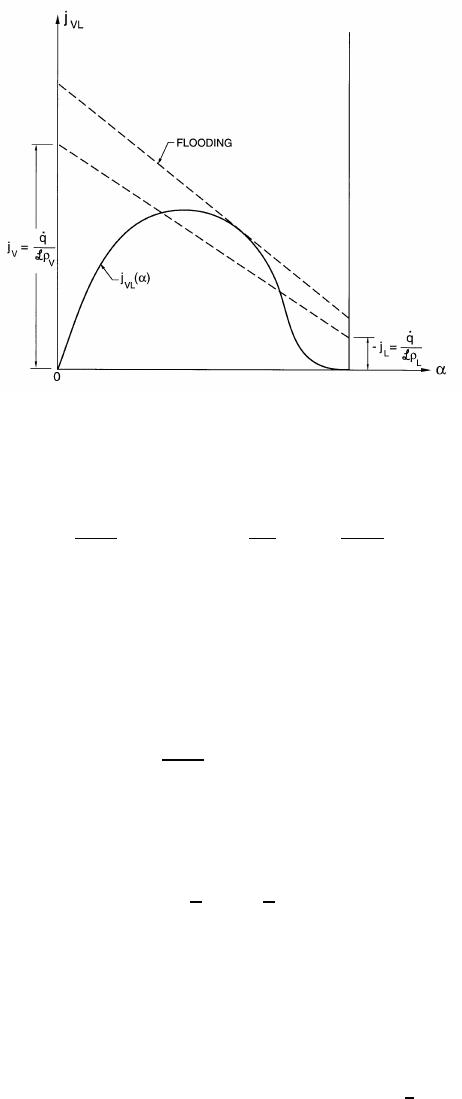
Figure 14.7. Drift ﬂux chart for boiling.

the intersection of the drift ﬂux curve, j

(α), with the dashed line

˙q



1 − α



1 −



≈

˙q

(1 − α) (14.9)

where the second expression is accurate when ρ

/ρ

 1asisfrequently

the case. It also follows that this ﬂow has a maximum heat ﬂux given by the

ﬂooding condition sketched in ﬁgure 14.7. If the drift ﬂux took the common

form given by equation 14.2 and if ρ

/ρ

 1 it follows that the maximum

heat ﬂux, ˙q

, is given simply by

˙q

= Ku

VL0

(14.10)

where, as before, u

VL0

, is the terminal velocity of individual bubbles rising

alone and K is a constant of order unity. Speciﬁcally,

K =



1 −



b−1

(14.11)

so that, for b =2,K =1/4 and, for b =3,K =4/27.

It remains to determine u

VL0

for which a prerequisite is knowledge of the

typical radius of the bubbles, R. Several estimates of these characteristic

quantities are possible. For purposes of an example, we shall assume that

the radius is determined at the moment at which the bubble leaves the wall.

If this occurs when the characteristic buoyancy force,

πR

g(ρ

− ρ

), is

339

balanced by the typical surface tension force, 2πSR, then an appropriate

estimate of the radius of the bubbles is

R =



2g(ρ

− ρ

)



(14.12)

Moreover, if the terminal velocity, u

VL0

, is given by a balance between the

same buoyancy force and a drag force given by C

πR

VL0

/2thenan

appropriate estimate of u

VL0



8Rg(ρ

− ρ

)

3ρ



(14.13)

Using these relations in the expression 14.10 for the critical heat ﬂux, ˙q

leads to

˙q

= C



Sg(ρ

− ρ

)



(14.14)

where C

is some constant of order unity. We shall delay comment on the

relation of this maximum heat ﬂux to the critical heat ﬂux, ˙q

,andon

the speciﬁcs of the expression 14.14 until the second model calculation is

completed.

A second approach to the problem would be to visualize that the ﬂow

near the wall is primarily within a vapor layer, but that droplets of water

are formed at the vapor/liquid interface and drop through this vapor layer

to impinge on the wall and therefore cool it (ﬁgure 14.8). Then, the ﬂow

within the vapor ﬁlm consists of water droplets falling downward through

an upward vapor ﬂow rather than the previously envisaged vapor bubbles

rising through a downward liquid ﬂow. Up to and including equation 14.11,

the analytical results for the two models are identical since no reference

was made to the ﬂow pattern. However, equations 14.12 and 14.13 must

Figure 14.8. Sketch of the conditions close to ﬁlm boiling.

340

be re-evaluated for this second model. Zuber et al. (1961) visualized that

the size of the water droplets formed at the vapor/liquid interface would be

approximately equal to the most unstable wavelength, λ, associated with

this Rayleigh-Taylor unstable surface (see section 7.5.1, equation 7.22) so

that

R ≈ λ ∝



g(ρ

− ρ

)



(14.15)

Note that, apart from a constant of order unity, this droplet size is func-

tionally identical to the vapor bubble size given by equation 14.12. This is

reassuring and suggests that both are measures of the grain size in this com-

plicated, high void fraction ﬂow. The next step is to evaluate the drift ﬂux

for this droplet ﬂow or, more explicitly, the appropriate expression for u

VL0

Balancing the typical net gravitational force,

πR

g(ρ

− ρ

) (identical to

that of the previous bubbly ﬂow), with a characteristic drag force given by

πR

VL0

/2 (which diﬀers from the previous bubbly ﬂow analysis only

in that ρ

has replaced ρ

)leadsto

VL0



8Rg(ρ

− ρ

)

3ρ



(14.16)

Then, substituting equations 14.15 and 14.16 into equation 14.10 leads to a

critical heat ﬂux, ˙q

,givenby

˙q

= C



Sg(ρ

− ρ

)



(14.17)

where C

is some constant of order unity.

The two model calculations presented above (and leading, respectively, to

critical heat ﬂuxes given by equations 14.14 and 14.17) allow the following

interpretation of the pool boiling crisis. The ﬁrst model shows that the

bubbly ﬂow associated with nucleate boiling will reach a critical state at

a heat ﬂux given by ˙q

at which the ﬂow will tend to form a vapor ﬁlm.

However, this ﬁlm is unstable and vapor droplets will continue to be detached

and fall through the ﬁlm to wet and cool the surface. As the heat ﬂux

is further increased a second critical heat ﬂux given by ˙q

=(ρ

/ρ

)

˙q

occurs beyond which it is no longer possible for the water droplets to reach

the surface. Thus, this second value, ˙q

, will more closely predict the true

boiling crisis limit. Then, the analysis leads to a dimensionless critical heat

341

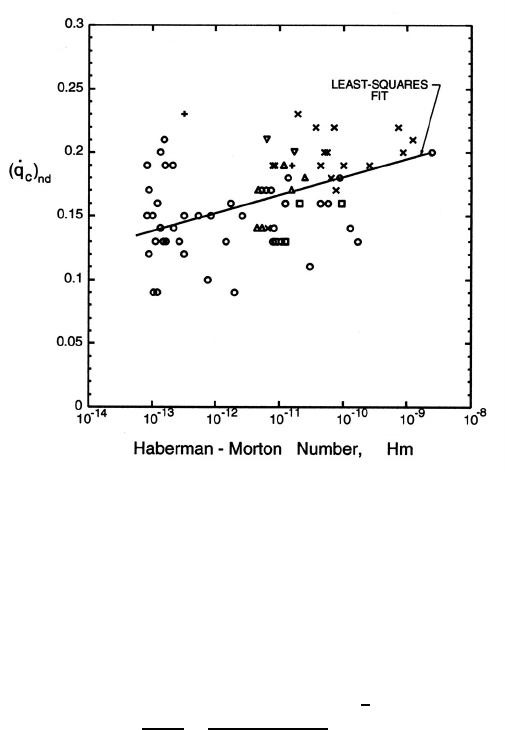
Figure 14.9. Data on the dimensionless critical heat ﬂux, ( ˙q

)

(or

), plotted against the Haberman-Morton number, Hm = gµ

(1 −

/ρ

)/ρ

,forwater(+),pentane(×), ethanol (), benzene (),

heptane() and propane (∗) at various pressures and temperatures.

Adapted from Borishanski (1956) and Zuber et al. (1961).

ﬂux, ( ˙q

)

, from equation 14.17 given by

(˙q

)

˙q



Sg(ρ

− ρ

)



−

= C

(14.18)

Kutateladze (1948) had earlier developed a similar expression using dimen-

sional analysis and experimental data; Zuber et al. (1961) placed it on a

ﬁrm analytical foundation.

Borishanski (1956), Kutateladze (1952), Zuber et al. (1961) and others

have examined the experimental data on critical heat ﬂux in order to deter-

mine the value of ( ˙q

)

(or C

)thatbestﬁtsthedata.Zuberet al. (1961)

estimate that value to be in the range 0.12 → 0.15 though Rohsenow and

Hartnett (1973) judge that 0.18 agrees well with most data. Figure 14.9

shows that the values from a wide range of experiments with ﬂuids includ-

ing water, benzene, ethanol, pentane, heptane and propane all lie within

the 0.10 → 0.20. In that ﬁgure ( ˙q

)

(or C

) is presented as a function of

the Haberman-Morton number, Hm = gµ

(1 − ρ

/ρ

)/ρ

, since, as was

342

seen in section 3.2.1, the appropriate type and size of bubble that is likely

to form in a given liquid will be governed by Hm.

Lienhard and Sun (1970) showed that the correlation could be extended

from a simple horizontal plate to more complex geometries such as heated

horizontal tubes. However, if the typical dimension of that geometry (say

the tube diameter, d) is smaller than λ (equation 14.15) then that dimension

should replace λ in the above analysis. Clearly this leads to an alternative

correlation in which ( ˙q

)

is a function of d; explicitly Lienhard and Sun

recommend

(˙q

)

=0.061/K

∗

where K

∗

= d/



g(ρ

− ρ

)



(14.19)

(the constant, 0.061, was determined from experimental data) and that the

result 14.19 should be employed when K

∗

< 2.3. For very small values of K

∗

(less than 0.24) there is no nucleate boiling regime and ﬁlm boiling occurs

as soon as boiling starts.

For useful reviews of the extensive literature on the critical heat ﬂux in

boiling, the reader is referred to Rohsenow and Hartnet (1973), Collier and

Thome (1994), Hsu and Graham (1976) and Whalley (1987).

14.4 CORRECTIONS FOR PIPE FLOWS

Before leaving this discussion of the use of drift ﬂux methods in steady ﬂow,

we note that, in many practical applications, the vertical ﬂows under consid-

eration are contained in a pipe. Consequently, instead of being invariant in

the horizontal direction as assumed above, the ﬂows may involve signiﬁcant

void fraction and velocity proﬁles over the pipe cross-section. Therefore, the

linear relation, equation 14.3, used in the simple drift ﬂux method to ﬁnd the

operating point, must be corrected to account for these proﬁle variations. As

described in section 1.4.3, Zuber and Findlay (1965) developed corrections

using the proﬁle parameter, C

(equation 1.84), and suggest that in these

circumstances equation 14.3 should be replaced by

=[1− C

α]j

− C

αj

(14.20)

where the overbar represents an average over the cross-section of the pipe.

343

SYSTEM INSTABILITIES

15.1 INTRODUCTION

One of the characteristics of multiphase ﬂows with which the engineer has to

contend is that they often manifest instabilities that have no equivalent in

single phase ﬂow (see, for example, Boure et al. 1973, Ishii 1982, Gouesbet

and Berlemont 1993). Often the result is the occurence of large pressure,

ﬂow rate or volume fraction oscillations that, at best, disrupt the expected

behavior of the multiphase ﬂow system (and thus decrease the reliability

and life of the components, Makay and Szamody 1978) and, at worst, can

lead to serious ﬂow stoppage or structural failure (see, for example, NASA

1970, Wade 1974). Moreover, in many systems (such as pump and turbine

installations) the trend toward higher rotational speeds and higher power

densities increases the severity of the problem because higher ﬂow velocities

increase the potential for ﬂuid/structure interaction problems. This chapter

will focus on internal ﬂow systems and the multiphase ﬂow instabilities that

occur in them.

15.2 SYSTEM STRUCTURE

In the discussion and analysis of system stability, we shall consider that the

system has been divided into its components, each identiﬁed by its index, k,

as shown in ﬁgure 15.1 where each component is represented by a box. The

connecting lines do not depict lengths of pipe which are themselves com-

ponents. Rather the lines simply show how the components are connected.

More speciﬁcally they represent speciﬁc locations at which the system has

been divided up; these points are called the nodes of the system and are

denoted by the index, i.

Typical and common components are pipeline sections, valves, pumps,

344

Figure 15.1. Flow systems broken into components.

Figure 15.2. Typical component characteristics, ∆p

(˙m

turbines, accumulators, surge tanks, boilers, and condensers. They can be

connected in series and/or in parallel. Systems can be either open loop or

closed loop as shown in ﬁgure 15.1. The mass ﬂow rate through a component

will be denoted by ˙m

and the change in the total head of the ﬂow across

the component will be denoted by ∆p

deﬁned as the total pressure at inlet

minus that at discharge. (When the pressure ratios are large enough so that

the compressibility of one or both of the phases must be accounted for, the

analysis can readily be generalized by using total enthalpy rather than total

pressure.) Then, each of the components considered in isolation will have a

performance characteristic in the form of the function ∆p

(˙m

)asdepicted

graphically in ﬁgure 15.2. We shall see that the shapes of these character-

istics are important in identifying and analysing system instabilities. Some

345

Figure 15.3. Typical system characteristic, ∆p

(˙m

), and operating point.

of the shapes are readily anticipated. For example, a typical single phase

ﬂow pipe section (at higher Reynolds numbers) will have a characteristic

that is approximately quadratic with ∆p

∝ ˙m

. Other components such as

pumps, compressors or fans may have quite non-monotonic characteristics.

The slope of the characteristic, R

∗

,where

∗

ρg

d∆p

d ˙m

(15.1)

is known as the component resistance. However, unlike many electrical com-

ponents, the resistance of most hydraulic components is almost never con-

stant but varies with the ﬂow, ˙m

Components can readily be combined to obtain the characteristic of

groups of neighboring components or the complete system. A parallel com-

bination of two components simply requires one to add the ﬂow rates at

thesame∆p

, while a series combination simply requires that one add the

∆p

values of the two components at the same ﬂow rate. In this way one

can synthesize the total pressure drop, ∆p

(˙m

), for the whole system as a

function of the ﬂow rate, ˙m

. Such a system characteristic is depicted in ﬁg-

ure 15.3. For a closed system, the equilibrium operating point is then given

by the intersection of the characteristic with the horizontal axis since one

must have ∆p

= 0. An open system driven by a total pressure diﬀerence of

∆p

(inlet total pressure minus discharge) would have an operating point

where the characteristic intersects the horizontal line at ∆p

=∆p

.Since

these are trivially diﬀerent we can conﬁne the discussion to the closed loop

case without any loss of generality.

In many discussions, this system equilibrium is depicted in a slightly dif-

346

Figure 15.4. Alternate presentation of ﬁgure 15.3.

ferent but completely equivalent way by dividing the system into two series

elements, one of which is the pumping component, k = pump, and the other

is the pipeline component, k = line. Then the operating point is given by

the intersection of the pipeline characteristic, ∆p

line

,andthepump charac-

teristic, −∆p

pump

, as shown graphically in ﬁgure 15.4. Note that since the

total pressure increases across a pump, the values of −∆p

pump

are normally

positive. In most single phase systems, this depiction has the advantage

that one can usually construct a series of quadratic pipeline characteristics

depending on the valve settings. These pipeline characteristics are usually

simple quadratics. On the other hand the pump or compressor characteristic

can be quite complex.

15.3 QUASISTATIC STABILITY

Using the deﬁnitions of the last section, a quasistatic analysis of the stabil-

ity of the equilibrium operating point is usually conducted in the following

way. We consider perturbing the system to a new mass ﬂow rate d ˙m greater

than that at the operating point as shown in ﬁgure 15.4. Then, somewhat

heuristically, one argues from ﬁgure 15.4 that the total pressure rise across

the pumping component is now less than the total pressure drop across the

pipeline and therefore the ﬂow rate will decline back to its value at the oper-

ating point. Consequently, the particular relationship of the characteristics

in ﬁgure 15.4 implies a stable operating point. If, however, the slopes of the

two components are reversed (for example, Pump B of ﬁgure 15.5(a) or the

operating point C of ﬁgure 15.5(b)) then the operating point is unstable

since the increase in the ﬂow has resulted in a pump total pressure that now

exceeds the total pressure drop in the pipeline. These arguments lead to the

347

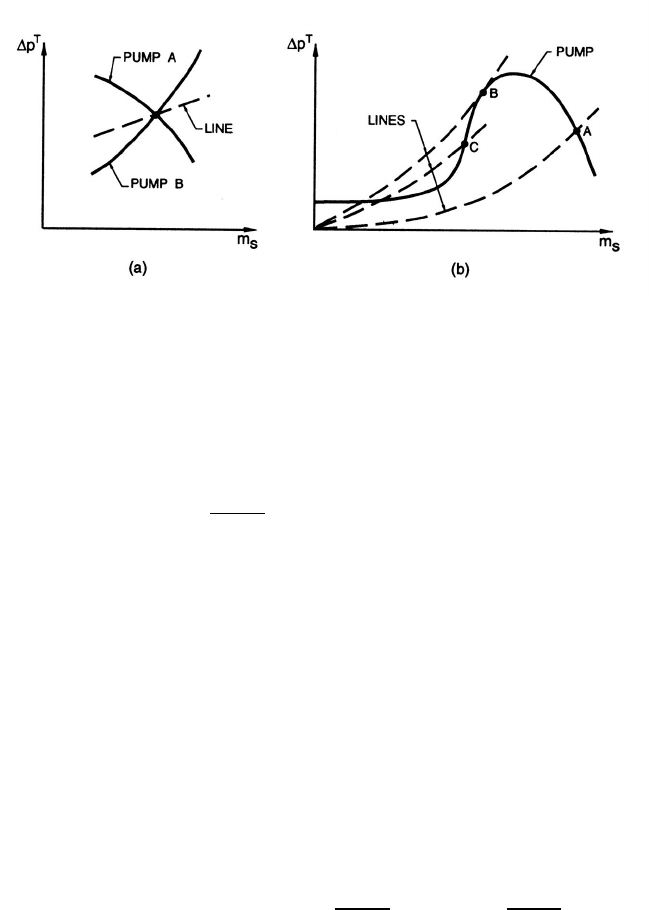
Figure 15.5. Quasistatically stable and unstable ﬂow systems.

conclusion that the operating point is stable when the slope of the system

characteristic at the operating point (ﬁgure 15.3) is positive or

d∆p

d ˙m

> 0 or R

∗

> 0 (15.2)

The same criterion can be derived in a somewhat more rigorous way by

using an energy argument. Note that the net ﬂux of ﬂow energy out of each

component is ˙m

∆p

. In a straight pipe this energy is converted to heat

through the action of viscosity. In a pump ˙m

(−∆p

) is the work done on

the ﬂow by the pump impeller. Thus the net energy ﬂux out of the whole

system is ˙m

∆p

and, at the operating point, this is zero (for simplicity we

discuss a closed loop system) since ∆p

= 0. Now, suppose, that the ﬂow

rate is perturbed by an amount d ˙m

. Then, the new net energy ﬂux out of

the system is ∆E where

∆E =(˙m

+ d ˙m

)



∆p

+ d ˙m

d∆p

d ˙m



≈ ˙m

d ˙m

d∆p

d ˙m

(15.3)

Then we argue that if d ˙m

is positive and the perturbed system therefore

dissipates more energy, then it must be stable. Under those circumstances

one would have to add to the system a device that injected more energy

into the system so as to sustain operation at the perturbed state. Hence the

criterion 15.2 for quasistatic stability is reproduced.

348