Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.

8.14 Weak Interactions and Quark Eigenstates 219
Table 8.3 Experimental measurements of the V
ij
elements of the CKM matrix
in the form (8.62c). To take into account the small CP violation, V
ub
must be
multiplied by the phase e
i
and V
td
by e
iˇ
[P10]
V
CKM
D
0
B
B
@
0:97428 ˙ 0:00015 0:2253 ˙ 0:0007 0:00347 ˙ 0:00016
0:2252 ˙ 0:0007 0:97345 ˙ 0:00015 0:041 ˙0:001
0:0086 ˙ 0:0003 0:040 ˙ 0:001 0:99915 ˙ 0:00005
1
C
C
A
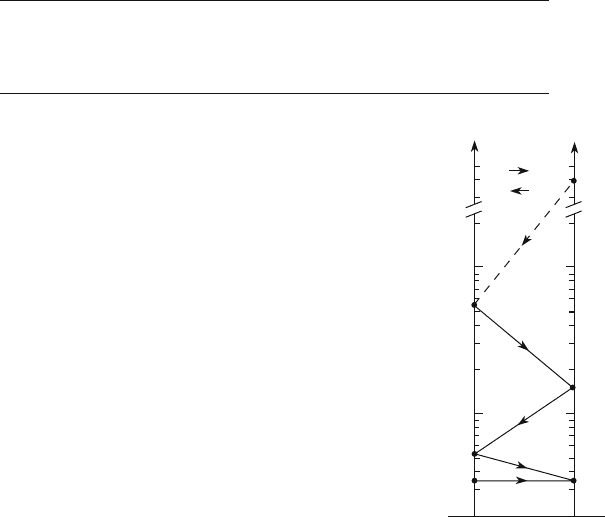
Fig. 8.20 Scheme of the
decay chain
t ! b ! c ! s ! u and
d ! u (t ! bW
C
,
b ! cW
, c ! sW
C
,
s ! uW
, d ! uW
).
Note that the mass of the d;u
quarks is 5 and 2.5 MeV,
that is, very small compared
to the other quark masses.
The mass of the t quark is
about 172 GeV [P10]
W
–
W
+
–1/3 +2/3
Charge
180
t
c
u
d
s
b
0.5
5
1
10
Quark mass (GeV)
where d
0
;s
0
;b
0
are the weak interaction eigenstates; d;s;b are the mass eigenstates
of the strong interaction (by convention, the u;c;t states are unchanged). The square
of the matrix element V
ud
gives the probability that an up quark turns into a down
quark, and similarly for the other matrix elements.
Experimentally, the off-diagonalelements of the CKM matrix in the form (8.62c)
are small (see Table 8.3); therefore, all mixing angles are small. This implies that
the model predicts a specific sequence of decays: starting from the top quark t,the
favored decay chain, shown in Fig. 8.20,is
t ! b ! c ! s ! u (8.63)
More precisely, one has: t ! bW
C
, b ! cW
, c ! sW
C
, s ! uW
,
d ! uW
).
With the introduction of the CKM mixing, quarks and leptons have the same
coupling for the weak interactions: this is the so-called lepton-quark universality.
The CKM matrix elements cannot by derived from the theory: they are free

220 8 Weak Interactions and Neutrinos
parameters in the Standard Model (Chap.11). The CKM elements are experimen-
tally determined [P10]: (1) V
ud
from the ratio of the neutron decay with respect to
the muon decay; (2) V
us
from the K
C
!
0
e
C
e
, K
0
L
!
˙
e
.
e
/ decays; (3)
V
cd
from charmed particle production in collisions with the d valence quark; (4)
V
cs
from the width of .D ! Ke
C
e
/ and from the hadronic decays of the W
˙
;
(5) V
cb
from the decay rate of B
0
! D
C
`
e
.
8.15 Discovery of the W
˙
and Z
0
Vector Bosons
The CERN Large Electron Positron collider (LEP), which operated from 1989
to 2001 (Chap. 9), was originally designed and built for the discovery of the
weak interactions W
˙
;Z
0
vector bosons. The LEP made many high precision
measurements of weak and electromagnetic interactions (electroweak interaction,
Chap. 11), including that of the vector boson masses. However, the discovery of
the W
˙
;Z
0
was anticipated in 1983 by a phenomenal intuition of C. Rubbia,
with the transformation of the CERN SPS into a collider machine (named Sp
pS).
When protons and antiprotons interact at high energy, a q
q annihilation takes place,
generating real (on mass shell) W
˙
or Z
0
bosons. The problem of accumulating a
large enough number of
p was solved by a technique (stochastic cooling) due to S.
van der Meer (with C. Rubbia, Nobel laureate in 1994). The W
˙
and Z
0
bosons
were observed through the following elementary processes:
u
d ! W
C
! e
C
e
; !
C
(8.64a)
d
u ! W
! e
e
; !
(8.64b)
(
u
u
d
d
)
! Z
0
! e
C
e
; !
C
: (8.64c)
In these processes, a quark of the proton annihilates with an antiquark of the
antiproton (Problem 10.6), producing a W
C
,aW
or a Z
0
which are observed
through their leptonic decays. These leptonic channels are relatively easy to
experimentally observe, see Fig. 8.21. The energy necessary to produce a real
W
˙
or Z
0
at rest is
p
s m
W
;m
Z
. If proton-proton collisions were used, the
annihilating antiquark must come from the “sea” (see Chap. 10).
Experimentally [8G84], the observed reactions were
p
p ! W
C
C X:::; W
C
! e
C
e
pp ! Z
0
C X:::; Z
0
! e
C
e
:

8.15 Discovery of the W
˙
and Z
0
Vector Bosons 221
d
u
–
u
u
–
z
p
p
–
u
d
–
W
–
W
–
e
–
J
Z
= 1
ν
–
e
θ
ab
Fig. 8.21 Observation of the W
vector boson at the CERN SppS collider in 1983. At a
fundamental level, the process is
ud ! W
! e
e
.(a) pp collision with a u quark of the
antiproton that annihilates with a d quark of the proton producing a W
boson almost at rest; (b)
the W
vector boson decays in e
C
e
The resulting cross-sections were evaluated by integrating the cross-sections for the
elementary q
q processes, each described by a Breit–Wigner formula, see Sect. 9.3.2.
For the production of a W
C
decaying into an e
C
e
pair, one has
u
d ! W
C
! e
C
e
D
1
N
c
4¯
2
ud
e
=4
.2s
d
C 1/.2s
u
C 1/
.E M
W
/
2
C
2
=4
2J C 1
3
(8.65)
where ¯ is the de Broglie wavelength in the c.m. of colliding quarks; ;
ud
;
e
are the total and partial widths (for W ! ud;W ! e), and s
d
D s
u
D 1=2 are
the quark spins. Only states with defined helicity are involved: left-handed fermions
and right-handed antifermions. The spin multiplicity for the W is .2J C 1/=3 D
3=3 D 1. N
c
is the color factor and 1=N
c
D 1=3 is the probability that a quark of
the proton “matches” an antiquark of the antiproton. At the energy E D M
W
,there
is a maximum, that is,
max
u
d ! W
C
! e
C
e
D
4
ud
e
3M
2
W
2
D
36M
2
W
' 5:2 nb; (8.66)
using M
W
D .80:22 ˙ 0:26/ GeV, a color factor of three for W ! ud;cs;tb and
one for W ! e
e
,
,and
and
ud
= D 1=4;
e
= D 1=12.
The cross-section for the processes (8.64c) involves the weak neutral current
which is (Chap. 11) about ten times smaller than the cross-sections of reactions
(8.64a, b). Both the W
˙
;Z
0
production and leptonic decays are rare processes,
at the level of 10
8
–10
9
of the total number of events. The total proton-antiproton
cross-section is
t
.pp/ ' 60 mb. These events (called minimum bias events)give
rise to final state hadrons with a low transverse momentum, Sect. 10.7. The W
˙
and Z
0
leptonic decays are relatively easy to detect because the leptons have a
high transverse momentum, p
t
M
W
=2 ' 40 GeV/c, without any appreciable
background from minimum bias events.
The W vector bosons couple with fermions/antifermions having spin antiparal-
lel/parallel to the momentum direction (e.g., left-handed electrons, e
L
,or

222 8 Weak Interactions and Neutrinos
right-handed positrons, e
C
R
). The W bosons do not couple with either the e
L
P -
conjugate particle, the e
R
, or with the C -conjugate particle, the e
C
L
.However,the
vector bosons couple with the e
L
CP -conjugate state, the e
C
R
.
8.16 The V-A Theory of CC Weak Interaction
The observation of the preferred W
˙
coupling with LH fermions (and RH an-
tifermions) and of the parity violation in weak interactions imposes some conditions
on the WI Hamiltonian. For spin 1/2 particles, the appropriate wave functions are
four-componentspinors that satisfy the Dirac equation. Below, we describe the weak
interaction developed in 1957 by Feynman and Gell–Mann (V A theory) as an
extension of the Fermi theory. The basic idea is formalized in analogy with the
electromagnetic interaction: the amplitude of the process is proportional to the four-
vector current density. The V A theory does not include the neutral currents, nor
the finite masses of the vector bosons. These features are included in the electroweak
theory of the Standard Model, presented in Chap. 11, which enlarges the V A
theory.
8.16.1 Bilinear Forms of Dirac Fermions
Electromagnetic interaction [A89]. We need to extend the definition of the matrix
element (4.29) obtained for the EM interaction without the assumption that fermions
are described by Dirac 4-spinors (see Appendixes A.3 and A.4, which should be
read before continuing with this section). When the Dirac theory is considered, the
matrix element M
if
for the transition probability can be represented as the product
of two “electromagnetic currents.”
Consider, for instance, the e
! e
elastic scattering; the matrix element
of this process can be written as
M
if
e
! e
/
˛
EM
q
2
e
e
D
˛
EM
q
2
J
J
: (8.67)
The transition e
! e
(electron current) is described by .
e
e
/ and the muon
current
!
by .
/. The electromagnetic interaction (EM) has a vector
(V ) nature and the operators which relate the initial, and the final 4-spinors are
the Dirac
matrices. The interaction between electric charges depends on ˛
EM
and occurs though a virtual photon exchange; these, as we already know, introduce
the propagator /
˛
EM
q
2
,whereq is the transferred four-momentum. The particle
currents can be now shortened by the symbol J
(where the index indicates that
the quantity is a four-vector: J
D .J
0
;
!
J/, with
!
J D .J
1
;J
2
;J
3
/) regardless of

8.16 The V-A Theory of CC Weak Interaction 223
whether it is due to an electron or a muon; indeed, the EM interaction only depends
on the electric charge.
In the case of electron scattering on a proton, the EM matrix element is
M
if
e
p ! e
p
˛
EM
q
2
J
J
baryonic
: (8.68)
The current due to the proton is denoted by J
baryonic
; the effect of the composite
structure of the proton shall be taken into account.
The vector nature of the EM interaction should now be explicitly introduced. For
this reason, we may indicate the vector current in (8.67)asJ
1
D V
1
and J
2
D V
2
:
M
if
e
! e
/
˛
EM
q
2
J
J
D
˛
EM
q
2
V
1
V
2
(8.69)
where
is the metric tensor (Appendix A.3). The explicit form is
V
1
V
2
D V
0
1
V
0
2
!
V
1
!
V
2
: (8.70)
Extension to the WI [8Pu84]. To extend the concept of current to weak interac-
tions, it should be written in the more general form, that is,
J
D O
i
: (8.71)
J
D .J
0
;
!
J/,where
!
J D .J
1
;J
2
;J
3
/. O
i
is the operator that defines the
interaction type; it is a combination of Dirac
matrices. The bilinear form (8.71)
behaves under Lorentz transformations as a scalar quantity (S), a pseudoscalar (P),
a vector (V), an axial-vector (A) and a tensor (T) according to the chosen operator
O
i
, where the index i can assume the values i D S;P;V;T;A. The relativistic
invariance properties (Problem 8.15) establish specific restrictions on the possible
shape of the current, as shown in the following table:
Number of Behavior Relative helicity of fermion
Current components under Parity and antifermion
S Scalar 1 C Same
V Vector
4 Spatial part: Opposite
T Tensor
6 Same
A Axial-vector
5
4 Spatial part: C Opposite
P Pseudoscalar
5
1
The operator of an interaction which occurs through the exchange of spin 1
particles (like the photon or the massive vector bosons W
˙
;Z
0
) may have a vector
or axial-vector structure. We shall show below that if the interaction conserves

224 8 Weak Interactions and Neutrinos
parity, it must be either purely vector or purely axial-vector. If parity is conserved,
vector bosons equally couple with LH and RH particles.
Parity operator. In Appendix A.4, we show that under the parity operator P ,the
four-dimensional spinor transforms as
P
!
0
: (8.72)
The matrix
0
allows the inversion of the spatial coordinates corresponding to the
parity operation. For
D
C
0
, one has the transformation
P
! .
0
/
C
0
D
C
0
0
D
0
.
Vector current. The vector current, for example, the electromagnetic V
D
,
transforms under parity as
P
!
0
.
0
/: (8.73a)
For time and space coordinates separately, one has
0
P
!
0
0
0
D
0
(8.73b)
k
P
!
0
k
0
D
k
(8.73c)
with k D 1,2,3. The spatial components change sign; the time component does not:
.V
0
;
!
V/
P
! .V
0
;
!
V/. Four-vectors V
which transform in this way are vector-
like. Equation 8.70 transforms under parity as
V
0
1
V
0
2
!
V
1
!
V
2
P
! V
0
1
V
0
2
!
V
1
!
V
2
D V
0
1
V
0
2
!
V
1
!
V
2
: (8.74)
The matrix element of electromagnetic interaction does not change under the parity
operator. QED is a vector theory (V ) which conserves parity.
Axial current (pseudovector). Let us now consider an axial current of the form
A
D
5
: (8.75)
Note that the
5
and
matrices anticommute:
5
D
5
.TheA
current
transforms under parity as
5
P
!
0
5
.
0
/: (8.76)
For time and space coordinates separately, one has
0
5
P
!
0
0
5
0
D
0
5
(8.77a)

8.16 The V-A Theory of CC Weak Interaction 225
k
5
P
!
0
k
5
0
D
k
5
(8.77b)
with k D 1,2,3. The time component changes sign, the spatial components do not:
.A
0
;
!
A/
P
! .A
0
;
!
A/,where
!
A D .A
1
;A
2
;A
3
/. The four-vectors A
which
transform in this way are known as axial-vectors (see Table 6.2). The matrix element
based on axial currents transforms under parity as
M
if
/ A
0
1
A
0
2
!
A
1
!
A
2
(8.78)
P
! M
if
/
A
0
1
A
0
2
!
A
1
!
A
2
D A
0
1
A
0
2
!
A
1
!
A
2
: (8.79)
The dot product of two axial-vectors is still invariant under parity.
Vector axial current. An operator consisting of a mixture of V and A is not
invariant under parity. The matrix element of a V A current is
M
if
/
V
1
A
1
V
2
A
2
(8.80)
D .V
0
1
A
0
1
/.V
0
2
A
0
2
/
!
V
1
!
A
1
!
V
2
!
A
2
: (8.81)
Under parity, M
if
transforms as
M
if
D
V
0
1
A
0
1
V
0
2
A
0
2
!
V
1
!
A
1
!
V
2
!
A
2
P
! M
if
D
V
0
1
C A
0
1
V
0
2
C A
0
2
!
V
1
!
A
1
!
V
2
!
A
2
D
V
0
1
C A
0
1
V
0
2
C A
0
2
!
V
1
C
!
A
1
!
V
2
C
!
A
2
:
Under parity, the matrix element transforms differently than a simple change of
sign of the space or time components. An observable constructed from vector and
axial-vector quantities (here, V A) changes, i.e., it is not conserved under a parity
transformation.
8.16.2 Current–Current Weak Interaction
The experimental data described in previous sections of this chapter unequivocally
indicate that the weak interaction vertex (with variation of the lepton electric charge)
is achieved through the exchange of a W
˙
vector boson and that it has a V A
structure. The V A choice (for example, with respect to V C A or T ) was guided
by experimental considerations, for example, the decay of charged pions.

226 8 Weak Interactions and Neutrinos
For the reaction
e
n ! e
p (Fig. 8.3), we can apply the current-current
formulation in order to write a matrix element with the same form as in the EM
case (8.68); the weak current J
must be necessarily different. The
e
n ! e
p
process is mediated by the W
˙
exchange and one can hypothesize that the process
arises through a n ! p transition (described by J
baryonic
), and a
e
! e
transition
(described by J
leptonic
). By analogy with (8.68c), the WI matrix element is
M
if
D G
F
J
leptonic
J
baryonic
D G
F
J
l
J
b
: (8.82)
The weak leptonic and hadronic currents can be written in the form
J
leptonic
D
e
O
i
I J
baryonic
D
p
O
i
n
: (8.83)
Let us analyze the leptonic current first.
Leptonic weak current. In the interaction vertex of the leptonic current of Fig.8.3,
an electron neutrino disappears and an electron appears. The most general form
of the leptonic current must take into account its vector or axial-vector character; it
can be written as
J
leptonic
J
l
D
c
V
V
l
C c
A
A
l
(8.84)
where V
;A
are respectively the vector and axial-vector currents, and c
V
;c
A
are
two numerical constants. However, only the choice
c
V
Dc
A
D 1 (8.85)
explains the observed phenomena described above, for example, the parity noncon-
servation in cobalt decay (Sect. 8.8), the helicity of the neutrino (Sect. 8.9)andthe
branching ratios of pion decay in muons and electrons (Sect. 8.10). Assuming the
quoted values of c
V
;c
A
,Eq.(8.84) can be explicitly written as
J
l
D
e
e
5
D
e
1
5
: (8.86)
With the following property of the matrices:
1
5
D
1
2
1 C
5
1
5
; (8.87)
Equation 8.86 can be written as
J
l
D 2
e
1 C
5
2
1
5
2
D 2.
e
/
L
.
/
L
: (8.88)
In the latter form, the leptonic WI charged current is formally analogous to that
for an EM photon exchange. The important difference is that only left-handed

8.16 The V-A Theory of CC Weak Interaction 227
fermions . /
L
couple with the W
˙
vector bosons. It is easy to show that right-
handed antifermions also couple with the W
˙
. In addition,
can be considered as
the wave operator which destroys the neutrino, while
e
is the operator that creates
the electron.
Weak baryonic current. Let us turn to the description of the baryonic part of (8.82).
In principle, transitions that do not change the nuclear angular momentum (J D 0,
Fermi transitions) can be associated with scalar .S/ and vector .V / currents. T; A
interactions may instead produce a nuclear spin variation J D 1, and can therefore
describe the Gamow–Teller transitions. The P (pseudoscalar) interaction contains
atermv=c where v is the nucleon velocity; in nuclear decay, one has v c; thus,
P does not give an important contribution to the transition probability. Moreover,
in the case of the pion decay (Sect. 8.10), the P interaction would give a helicity
factor equal to .1 C v
=c/, which would lead to the ratio of branching ratios
defined in (8.39) equal to R D 5:5, in complete disagreement with the experimental
results.
In terms of elementary constituents, protons and neutrons are made of spin
1/2 fermions (quarks) which, regarding their spinorial nature, have characteristics
similar to those of the leptons. One may assume that the baryonic weak current
operators are composed of a linear combination of V;A terms. This was experi-
mentally confirmed from radioactive decays, the analysis of the ˇ decay spectra,
the study of the correlations between the electron and neutrino momenta, and the
nuclear lifetime measurements (see Sect. 8.6).
AsshowninFig.8.3c, the baryonic current is actually considered as a transition
from a quark d to a quark u (with a variation of one unit of electric charge), d ! u;
by neglecting the spectator quark contribution, the baryonic current can be written
in analogy to (8.86), that is,
J
baryonic
J
b
D g
V
u
d
C g
A
u
5
d
(8.89)
where g
V
;g
A
are vector and axial-vector coupling constants which can be written as
g
V
D cos
C
c
V
(8.90a)
g
A
D cos
C
c
A
(8.90b)
where
C
is the Cabibbo angle (see Sect. 8.12)andc
V
;c
A
are the respective
couplings with the vector and axial-vector components of the current. Assuming
the universality of fermions, one has c
V
Dc
A
D 1asin(8.85).
The constant appearing in (8.90b) can be calculated in the 4-spinors Dirac
theory, and is D5=3 [P95]. If we assume that there is no interference between
the vector and axial-vector amplitudes, the total contribution to the transition
probability (8.82)is
jMj
2
jM
if
j
2
=G
2
F
D
g
2
V
C 3g
2
A
(8.91)
228 8 Weak Interactions and Neutrinos
where the factor three in the axial part takes into account the spin 1 state multiplicity
(the factor is m
i;s
defined in Sect. 8.6). This is the exact term that should be included
in the formula for neutron decay (8.11).
If we assume that the Fermi constant G
F
is known from the muon decay, the
quantity .g
2
V
C3g
2
A
/ can be determined from the neutron lifetime measurements (as
the kinematic factors are known). To separate g
V
from g
A
, a second quantity must be
independently measured. The asymmetry in the decay of polarized neutrons [P10]
was chosen. The combination of these two measurements gives
g
A
g
V
D1:267 ˙ 0:004: (8.92)
This value should be compared with that of (8.26); it confirms (given the value of
the Cabibbo angle
C
)thatc
V
D 1. Note that the measured values of are not
exactly those expected for point-like Dirac particles ( D1:666). This is due to
the presence of strongly interacting spectator quarks that change the spin dependent
part of the interaction. This induces some effects on the axial-vector component of
the weak baryonic current.
In general, it is expected
5
that in leptonic decays (e.g., that of the muon), one
has c
A
=c
V
D D1. In processes involving hadrons, the perturbation due to the
strong interaction slightly changes the value: in the S D 0n! pe
e
decay,
D1:27, while in the S D 1 decay,
0
! pe
e
,itis D0:69.
5
This part of the weak interaction theory is called PCAC, that is, Partially Conserved Axial-vector
Current [8V84].
