Braibant S., Giacomelli G., Spurio M. Particles and Fundamental Interactions: An Introduction to Particle Physics
Подождите немного. Документ загружается.


4.7 A Few Examples of Electromagnetic Processes 97
θ
∗
e
+
e
+
e
+
μ
+
μ
+
μ
+
μ
–
γ
e
–
e
–
e
–
μ
–
μ
–
Z
0
s channel
t channel
abc
Fig. 4.10 Feynman diagrams for the reaction e
C
e
!
C
caused by (a) electromagnetic
interaction and (b) through the weak neutral current. Note that the reaction in the s channel is
e
C
e
!
C
while in the t channel, it is e
C
! e
C
.(c) Illustration of the collision
e
C
e
!
C
in the c.m. system
coinciding with Eq. 4.54 obtained with the classical calculation, see also
problem 4.6. This equation is valid for any electric charge, assuming a target particle
much heavier than the incident one. For example, this is the case for the e
p
scattering (Z D z D 1). The study of this process shall be extended in Chap. 10
in order to include the finite mass of the interacting particles, their spin and the
finite size of the proton. Note that Eq. 4.60 depends on E
2
c
: the probability of a
particle to be elastically scattered through the electromagnetic interaction decreases
quadratically with increasing kinetic energy of the incident particle.
4.7.2 The e
C
e
!
C
Process
(This and the following subsections are more advanced, and can be skipped during
the first reading). The annihilation of an electron–positron pair with the creation
of a muon–antimuon pair is a typical example of an electromagnetic process
whose cross-section can be calculated with Feynman diagrams. The result of the
calculation is used in Sect. 9.3 which describes the discovery of heavy quarks.
The electromagnetic cross-section for the reaction e
C
e
!
C
can be
obtained from the lowest order Feynman diagram of Fig. 4.10a. The cross-section
is proportional to ˛
2
EM
(because two vertices are present). The e
C
e
annihilation
generally occurs in colliders where particle and antiparticle have momentum equal
in magnitude and opposite in direction. In this case, the relativistically invariant q
2
coincides (in natural units) with the c.m. energy s.Usingp
2
D s, one obtains an
equation similar to (4.59), that is,
˛
2
EM
.„c/
2
s
: (4.61a)
The resulting angular distribution for nonpolarized e
C
;e
beams is given by
d
d˝
D
˛
2
EM
4s
.1 C cos
2
/ (4.61b)
98 4 The Paradigm of Interactions: The Electromagnetic Case
0
50
100
150
–0.8 –0.6 –0.4 –0.2 0 0.2 0.4 0.6 0.8
cos θ
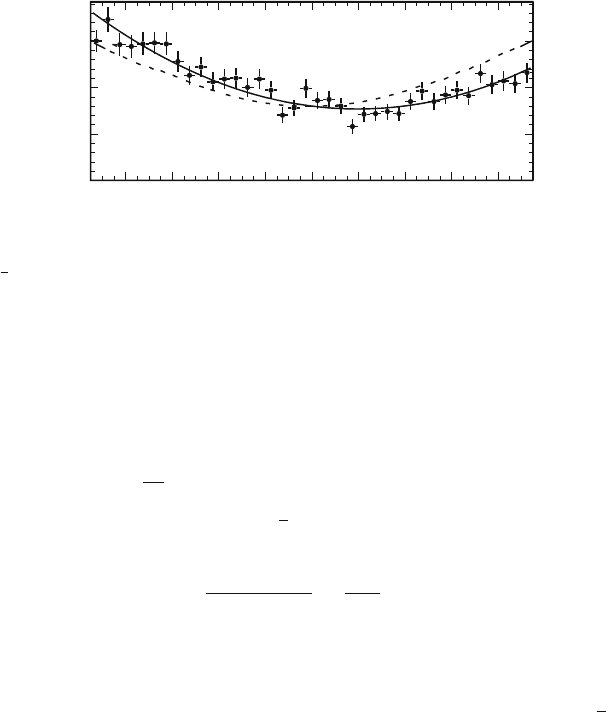
Fig. 4.11 Angular distribution in the c.m. system of the
, from the process e
C
e
!
C
at
p
s ' 89 GeV. The dashed line represents the .1 C cos
2
/ shape predicted by the EM
interaction; the solid line is the optimization of experimental data in which a small effect due
to weak interactions (diagram of Fig.4.10b) is included
where
is the emission angle of the muon in the c.m. system (see Fig. 4.10c). The
term .1Ccos
2
/ comes from the e
C
, e
total angular momentum: J D 0 or J D 1
if their spin are antiparallel or parallel. For J D 0, as discussed in Sect. 7.5.1, the
differential cross-section has no angular structure; for J D 1, angular momentum
conservation requires
d
d˝
/ cos
2
.
The integration on the solid angle of (4.61b) for energies well above the muon
mass (this process has a threshold of
p
s D 2m
c
2
) leads to
.e
C
e
!
C
/ D
4˛
2
EM
.„c/
2
3s
D
86:8
s
nb if s in GeV
2
; (4.62)
where s D .2E
0
/
2
with E
0
D energy of the colliding electron and positron in the
c.m. system. The factor 4=3 is derived from the integration over the solid angle.
The experimental angular distributions at relatively low energies are in agreement
with the .1 C cos
2
/ shape of (4.62), but at higher energies, for example,
p
s>
20 GeV, a disagreement is clearly visible in Fig. 4.11.Thee
C
e
!
C
can
also occur through the exchange of a Z
0
, as shown in Fig. 4.10b. This process is
a pure weak interaction process (neutral current). It becomes more important with
increasing c.m. energy, reaching a maximum at energies corresponding to the Z
0
boson mass. This topic shall be discussed in Chap. 9. We shall see in Chap. 11
that at high energy, the electromagnetic and weak interactions give rise to a unified
electroweak interaction.
4.7.3 Elastic Scattering e
C
e
! e
C
e
(Bhabha Scattering)
The two EM diagrams of Fig. 4.6a,b contribute to this process. The s channel
diagram shown in Fig. 4.6b produces a result similar to that obtained with the graph
of Fig. 4.10afore
C
e
!
C
. The diagram of Fig.4.6a is similar to that for the

4.7 A Few Examples of Electromagnetic Processes 99
elastic scattering and produces a term which dominates at small diffusion angles.
The corresponding cross-section rapidly increases with decreasing angle. The two
vertices contribute to the matrix element M
if
, each with a
p
˛
EM
; the photon
propagator contributes with a term 1=q
2
. Therefore, the cross-section is proportional
to
d
dq
2
M
2
if
˛
2
EM
q
4
. The correct formula for relativistic electrons (obtained using
the full QED procedure [H84]) is
d
dq
2
D
4˛
2
EM
.„c/
2
q
4
c
2
cos
2
2
: (4.63)
The weak interaction diagram shown in Fig. 4.6c must be added to the two EM
diagrams. The result provides a complicated angular distribution, in which the
behavior can be roughly described by two contributions: at small angles, the cross-
section has a dependence in 1=
4
1=q
4
due to the EM terms; at large angles, the
situation is similar to that of the process e
C
e
!
C
(see Fig.4.11).
The total cross-section for the Bhabha scattering has a 1=s energy dependence,
as the e
C
e
!
C
process. This is a characteristic of the EM interaction.
The large cross-section at small angles is only due to the EM interaction and is
calculated with a precision better than 1%. Electron–positron colliders (for example,
the LEP at CERN) use the measurement of the Bhabha cross-section at small angles
to derive the collider luminosity. An accurate luminosity measurement is necessary
for precise measurements of the cross-sections of other processes (Chap.10).
4.7.4 e
C
e
! Annihilation
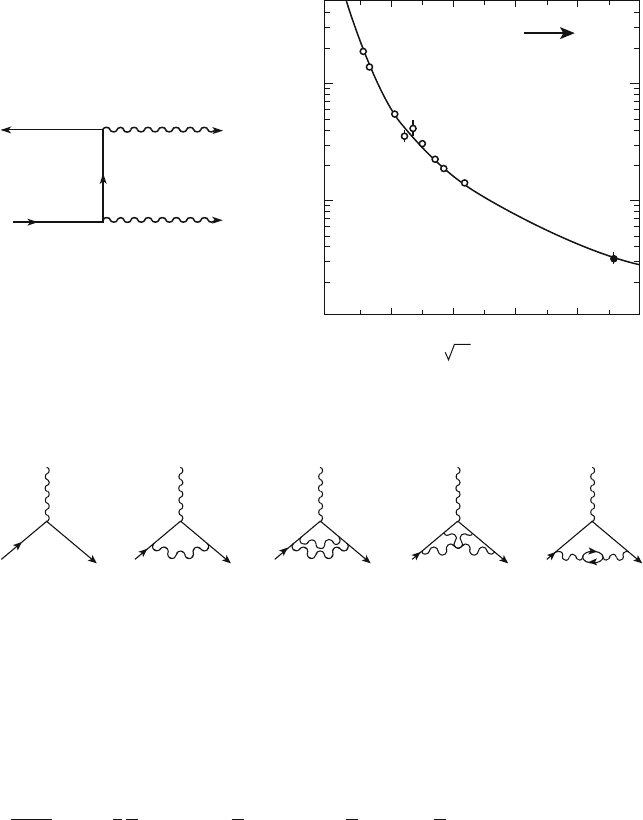
The production of a photon pair in an e
C
e
annihilation offers the possibility to
check the QED validity at the highest available energies. At the lowest order, the
process takes place through the exchange of an electron, as shown in the Feynman
diagram of Fig. 4.12a; therefore, this process only involves the EM interaction and
the terms due to the weak interaction are negligible. The cross-section due to this
diagram is
T
D
2˛
2
s
ln
s
m
2
e
: (4.64)
Experimental results on the total cross-section are in good agreement with the
predictions of Eq.4.64 (see Fig.4.12b).
4.7.5 Some QED Checks
Checks of the QED have been made with great precision in many fields of particle
physics. The most accurate test arises from the measurement of the electron and
muon magnetic moments. The lowest order Dirac theory predicts that the magnetic
moments of both particles are equal to one Bohr magneton
Bohr
D e„=2m
100 4 The Paradigm of Interactions: The Electromagnetic Case
e + e
–
10
3
10
2
10
0 20406080100
σ (IcosθI < 0.9) (pb)
e
e
+
γ
γ
e
–
γγ
(GeV)
s
a
b
Fig. 4.12 e
C
e
! process: (a) first order Feynman diagram and (b) total cross-section as a
function of c.m. energy (LEP data)
e
–
e
–
e
–
e
–
e
–
e
–
e
–
e
–
e
–
e
–
ab c d e
Fig. 4.13 Feynman diagrams for the interaction between the magnetic moment of the electron
with an external B field. (a) lowest (leading) order, (b) next-to-leading order, (c–e) next-to-next-
to-leading order [W91]
(with m D m
e
;m
). The radiative corrections accounts for the interaction of the
electron (muon) with the magnetic field needed to make the measurement (see
Fig. 4.13). The radiative corrections modify the ratio as .˛ D ˛
EM
/:
e
Bohr
D 1 C
1
2
˛
0:32848
˛
2
C 1:1765
˛
3
0:8
˛
4
D 1:001159652307.11/:
(4.65)
The experimental value is 1.001 159 652 193 (10) (the last two numbers in the
bracket represents the experimental uncertainty). The theoretical error is due to the
uncertainty on higher order diagrams.
An agreement experiment-theory of the same order of magnitude is also obtained
for the magnetic moment of the muon. Note that one often refers to the value of
(g 2/ where g is the gyromagnetic ratio expected to be equal to two with the
lowest order diagram. Other QED precision tests will be discussed in Chap. 9.

Chapter 5
First Discussion of the Other Fundamental
Interactions
5.1 Introduction
It the last chapter, we learned that the electromagnetic interaction between particles
occurs through momentum exchange. Classically, this exchange is due to a field:a
particle is a source of one or more fields through which it modifies the properties of
the surrounding space. A second particle within the range of the first particle field
and which generates the same field is subject to a force. Due to the field created
by the second particle, the first particle “feels” the same force but in the opposite
direction (third principle of dynamics). A field can only be measured through its
effects on another source of the same field.
In terms of quantum mechanical laws and in analogy with QED, any interaction
between two fermionic particles is seen as the process of emission/absorption of a
virtual bosonic particle. These virtual bosonic particles are “carriers” of the field.
Virtual particles cannot be directly observed because they are “hidden” by the
uncertainty principle.
Presently, four types of interactions are known: the gravitational, weak, elec-
tromagnetic and strong interactions. The electromagnetic interaction was presented
in the previous chapter. Here, we will give a semiquantitative introduction of the
remaining three. The gravitational interaction is negligible at the submicroscopic
level (except for the first moments of the universe, as we shall see in Chap. 13) and
will no longer be considered in the remainder of the book.
5.2 The Gravitational Interaction
From a historical point of view, the gravitational force (the first known interaction)
can be regarded as the “unification” of two interactions. Until the formulation of
Newton (Philosophiae Naturalis Principia Mathematica, 1687), the attraction force
between the sun and the planets, and the weight of objects on Earth’s surface were
S. Braibant et al., Particles and Fundamental Interactions: An Introduction to Particle
Physics, Undergraduate Lecture Notes in Physics, DOI 10.1007/978-94-007-2464-8
5,
© Springer Science+Business Media B.V. 2012
101

102 5 First Discussion of the Other Fundamental Interactions
considered as two distinct forces. Newton realized that the force that ties the planets
to the sun, and the moon to the earth is the same force as that responsible for the fall
of bodies on earth. The gravitational force is expressed by
F DG
N
m
1
m
2
r
2
O
r (5.1)
where m
1
and m
2
are the gravitational masses of the two interacting bodies, r is the
distance between them,
O
r is a unit vector directed from m
1
to m
2
,andG
N
is the
gravitational constant
G
N
D 6:672 10
8
cm
3
g
1
s
2
D 6:672 10
11
Nm
2
kg
2
:
The gravitational mass is always positive and therefore, the gravitational force is
always attractive.
It is an experimental fact and a principle of general relativity that the ratio
between the inertial mass .m
i
/ and the gravitational mass .m
g
/ is constant for all
bodies. In our metric system, m
i
and m
g
are dimensionally and numerically equal.
Each interaction can be characterized by a dimensionless parameter expressed in
terms of universal constants; these coupling constants (similar to ˛
EM
) characterize
the intensity of the interactions (see Table 5.1). For gravity, taking the proton mass
as the fundamental mass, the corresponding dimensionless quantity is
˛
G
D G
N
m
2
p
„c
D 6:673 10
11
.1:67 10
27
/
2
1:05 10
34
3:00 10
8
D 5:90 10
39
: (5.2)
In terms of universal constants, two other quantities related to the gravitational
interaction can be constructed. The first is the Planck mass
M
Pl
D
p
„c=G
N
D
p
3:1638 10
26
=6:673 10
11
D 1:221 10
19
GeV (5.3)
which is a huge mass compared to the most massive particles known today, i.e.,
100 GeV for the weak vector bosons and 170 GeV for the top quark. The second
quantity is the Planck length
`
Pl
D
„c
M
Pl
c
2
D 1:616 10
35
m : (5.4)
Note that the Planck length is 10
20
smaller than the proton size.
A satisfactory quantum theory of gravitation still does not exist. It is expected
that the particle carrier of the gravitational field, the graviton, should have spin two,
and zero mass (the mass is inversely proportional to the range of the force, which
is infinite). The gravitational force plays a fundamental role in the macrocosm. At
the subatomic level, the gravity is completely negligible compared to the other three
interactions: if the hydrogen atom was held together by only the gravitational force,
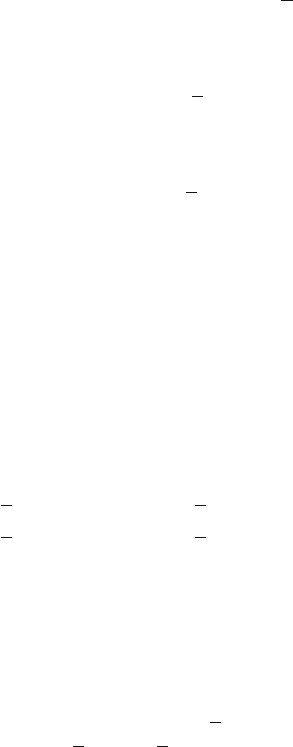
5.3 The Weak Interaction 103
its size would be larger than that of the universe. It is assumed that the gravitational
interaction becomes important for distances of the order of the Planck length and
energy (and mass) above the Planck mass.
5.3 The Weak Interaction
The weak interaction (WI) was initially investigated while studying the radioactive
decays of atomic nuclei (Chap. 14). The ˇ decay of a nucleus A.Z; N / with mass
number A, with Z protons and N neutrons, occurs in the following such that
A.Z; N / ! A.Z C 1; N 1/e
e
: (5.5a)
This process corresponds to a neutron decay
n ! pe
e
(5.5b)
which, at the fundamental level, corresponds to the decay of a d quark
d ! ue
e
: (5.5c)
The nucleons (protons and neutrons) in (5.5a) and quarks in (5.5b), which do not
participate in the decay, are called “spectators.”
At the level of the ultimate constituents of matter, the weak interaction takes
place between two quarks, two leptons and between a lepton and a quark. Quarks
and leptons can be thought of as having a weak charge. The weak interaction is less
intense than strong and EM interactions. In most cases, it is “overwhelmed” by the
strong and EM interactions, unless these cannot act due to some conservation law.
The weak interaction is responsible for all processes in which neutrinos are
involved. Neutrinos have neither a strong charge (color charge) nor an electric
charge. Examples of neutrino interactions on protons and electrons are
8
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
<
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
:
High energy
interaction
p !
C
n.a/
High energy
e
interaction
e
p ! e
C
n.b/
(Charged Current interaction)
Elastic scattering
e
e
!
e
.c/
(Neutral Current interaction).
(5.6)
The ˇ decay of a neutron (5.5b) is an example involving a neutrino. Note that the
neutron cannot have other types of decay because of baryon and lepton number
conservation (Sect. 5.5.3): a proton and an e
;
e
pair must be present in the final
state. Neutron decay into p
or p
are energetically forbidden.
104 5 First Discussion of the Other Fundamental Interactions
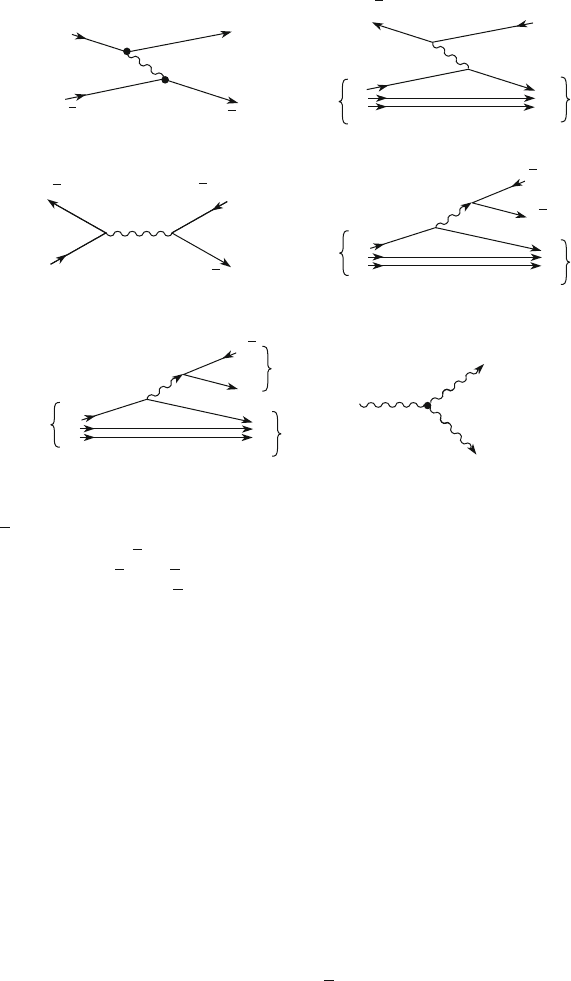
u
ν
μ
ν
μ
ν
e
g
g
Z
0
u
d
e
e
e
W
–
π
−
Σ
−
W
–
d
d
s
d
d
u
n
d
a
c
e
ν
μ
ν
e
μ
+
W
–
d
u
d
d
u
u
u
d
d
u
d
u
p
n
p
n
W
–
e
W
–
W
+
Z
0
b
d
f
Fig. 5.1 Weak interaction Feynman diagrams. (a) Elastic scattering
e
!
e
, mediated
through a Z
0
boson (neutral current weak interaction); g represents the coupling constant.
(b)
p !
C
n interaction mediated through a W
boson (charged current interaction). The
elementary process is
u !
C
d, with the remaining u, d quarks acting as “spectators.”
(c) Charged current
ud !
e
e
interaction involving quarks, mediated through a W
boson.
(d) Neutron decay, n ! pe
e
; quarks d, u act as “ spectators,” the basic process is similar to that
shown in (c), with the transformation of the incoming d quark into an outgoing u.(e) ˙
! n
decay. (f) Triple vertex between Z
0
;W
C
and W
bosons
Quark interactions and decay processes involving a quark flavor change (see
Chap. 7) with a variation in strangeness S or charm C quantum numbers .S 6D 0,
C 6D0/ are forbidden in strong and EM interactions. Those processes can therefore
be used to study the weak interaction. The nonleptonic decay of the ˙
hyperon
(Fig. 5.1e) is an example of a decay with a flavor change:
˙
! n C
S 100
(5.7a)
which involves the transformation of a strange quark s (S D1) into a nonstrange
quark u (S D 0). Similarly to the neutron decay, one has at the quark level
(Fig. 5.1d):
˙
(
s ! uW
! u.d u/ ! u
dd dd dd dd
)
! n
(5.7b)
with the two dd quarks of the initial ˙
acting as spectators.

5.3 The Weak Interaction 105
The weak interaction is mediated through the massive vector bosons, W
˙
and Z
0
, respectively with a mass of 80.3and 91.2 GeV. The processes with a
W
C
or W
exchange are called Charged Current interactions. They involve the
transformation of a lepton into another lepton of the same family (see reactions
(5.6a,b)) and of a quark into a different flavor quark. The processes with a Z
0
exchange are called Neutral Current interactions (see reaction (5.6c)). Figure 5.1
illustrates the interpretation of processes such as (5.6) in terms of quarks and
leptons exchanging a W
C
;W
or Z
0
vector boson. Note that the leptonic weak
vertices involve only members of the same family (D generation). The emission
(or absorption) of a W boson by a lepton transforms a member of the family
into the other, and vice versa (e
$
e
I
$
I $
). As discussed
in Chap. 8, transitions between different families are allowed in the quark sector.
“Spectator” quarks present in weak processes with hadrons are later involved in the
hadronization process (Chap.10).
An estimate of the intensity of the weak interaction with respect to the EM
one can be obtained by comparing the lifetimes of decays involving particles with
similar masses, but due to different interactions, that is,
Weak interaction
!
WI
D 2:6 10
8
10
8
s
Electromagnetic interaction
0
!
EM
D 8:4 10
17
10
16
s:
The ratio between the two lifetimes is related to the inverse of the ratio between
transition amplitudes: .
WI
=
EM
/ W
EM
=W
WI
/, (4.43). The “weak” diagram of
Fig. 5.1e can be interpreted in a similar manner to that of the EM interaction of
Fig. 4.1. The contribution of the two vertices to the scattering amplitude is W
WI
/
˛
W
˛
W
D Œgg
2
,whereg may be thought of as the “weak” equivalent of the electric
charge. For the electromagnetic interaction, one has W
EM
/ ˛
EM
˛
EM
D Œe
2
2
.
It follows that
˛
W
˛
EM
/
EM
WI
1=2
'
10
16
10
8
1=2
' 10
4
: (5.8)
This is a rough estimate, which neglect some factors, but sufficient to show that
the weak interaction is much weaker than the electromagnetic one. The “magic” of
being able to estimate the particle lifetimes when the coupling constant is known
shall be discussed in detail in Chap. 8.
The weak interaction bosonic propagator must take into account the fact that the
.W
˙
;Z
0
/ masses are large. According to (4.32), the transition probability for the
weak interaction W
WI
(Sect. 4.4) becomes
W
1=2
WI
/ f.q
2
/ D
g
2
q
2
C m
2
W;Z
0
D
˛
W
q
2
C m
2
W;Z
0
: (5.9)

106 5 First Discussion of the Other Fundamental Interactions
At low energies, one has q
2
m
2
W;Z
0
and therefore f.q
2
/ ' g
2
=m
2
W;Z
0
Dconstant,
independent of q
2
. Because the Fourier transform of a constant in momentum space
is a Dirac delta function in the coordinate space, the interaction is practically point-
like, as Fermi postulated in 1935. For q
2
m
2
W;Z
0
, one can write
G
F
p
2
D
g
2
8m
2
W
(5.10)
where G
F
is the Fermi coupling constant, G
F
=.„c/
3
D 1:1664 10
5
GeV
2
.
The dimensionless constant of the weak interaction can be constructed using, for
example, the proton mass m
p
as the reference mass
˛
W
D .m
p
c
2
/
2
G
F
.„c/
3
D .0:932827/
2
1:1664 10
5
D 1:027 10
5
: (5.11)
The weak coupling g D
p
˛
W
is not constant, but increases with energy with a
dependence stronger than that of ˛
EM
(Chap. 11).
The weak interaction violates a number of conservation laws. For example, it
violates the conservation of parity (Sect. 6.4). Assuming that neutrinos are mass-
less,
1
the weak couplings of right-handed neutrinos and left-handed antineutrinos
are null. Therefore, neutrinos are always left-handed, that is, the neutrino spin (()
is antiparallel to the momentum .!/: D .
!
(
). The antineutrinos are always
right-handed, i.e., with parallel spin and momentum:
D .
!
)
).
A “triple” vertex involving the vector bosons Z
0
;W
C
and W
(see Fig. 5.1f)
is also theoretically allowed. Due to the high mass of the Z
0
;W
˙
bosons, the
contribution of this vertex is negligible at low energy. It becomes important in
e
C
e
! Z
0
! W
C
W
collisions, for
p
s 2m
W
' 161 GeV (Chap. 9).
5.4 The Strong Interaction
At the fundamental level, the strong interaction takes place between quarks and
gluons (Fig. 5.2). It controls the collisions between two quarks, the interaction
between three quarks to form a baryon, or between a quark and an antiquark to
form a meson.
It can be assumed that the force between two nucleons (Chap. 14) is a “residual”
strong force, similar to the electromagnetic force between two atoms to form
1
Recent experimental results on neutrino oscillations demonstrate that neutrinos have a very small,
but nonzero, mass (Sect. 12.6).
