Бормотов А.Н. Полимерные композиционные материалы для защиты от радиации

Подождите немного. Документ загружается.

Синтез композиционных материалов как задача управления

2.2. Иерархические структуры радиационно-защитного компози-

та и критериев его качества

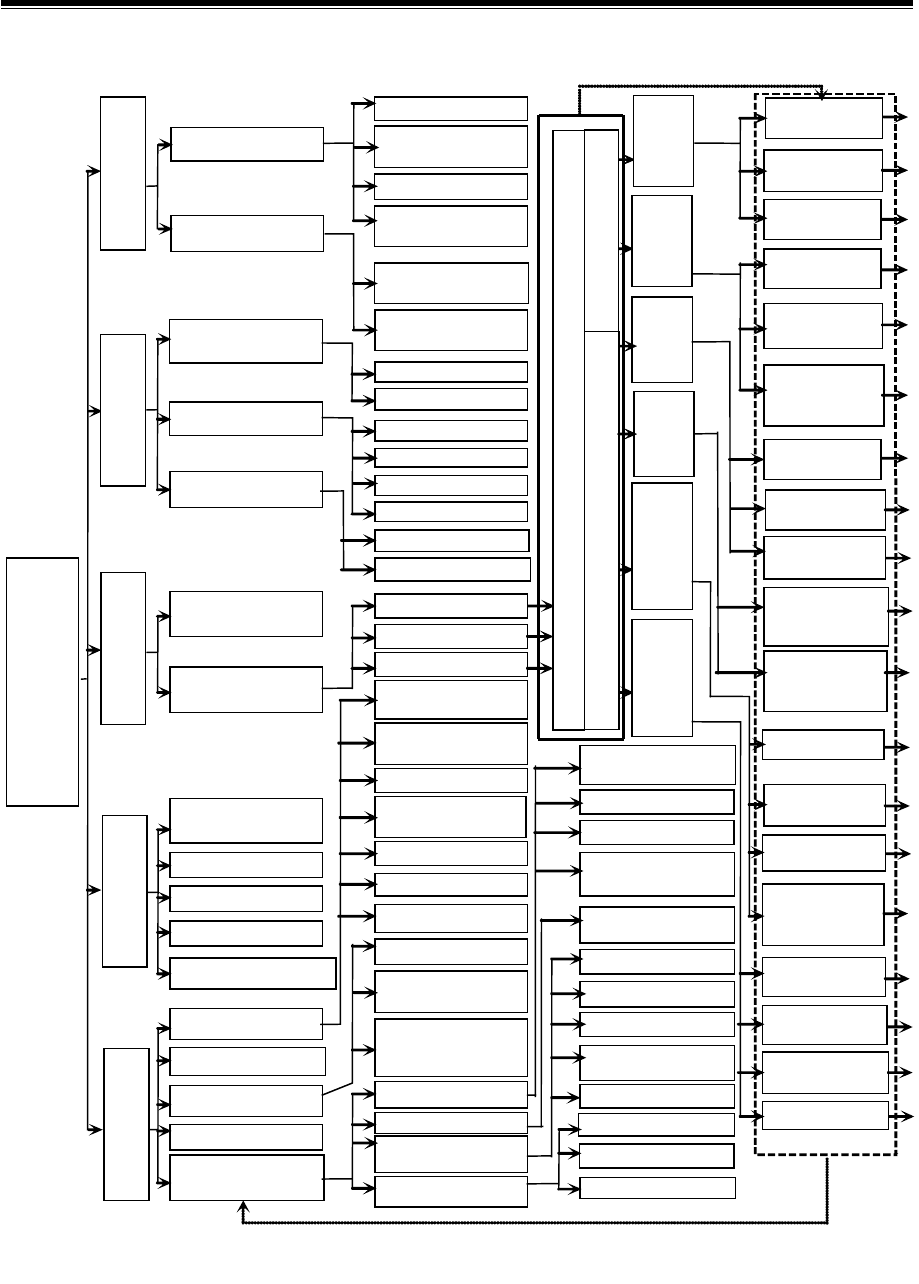
В иерархической структуре критериев эффективности системы (ра-

диационно-защитного композита) на верхнем (

первом) уровне находятся

следующие основные критерии: полезность системы (выходные характе-

ристики материала, важность, актуальность, перспективность, область

применения (критерии

второго уровня)); качество функционирования

(помехозащищенность, точность, надежность, чувствительность, качество

управления); организация системы (совершенство структуры, сложность и

т.д.); эволюционная эффективность (осуществимость, ресурсы, возможно-

сти модификаций и др. характеристики развития); экономическая эффек-

тивность (рис. 2.2).

Декомпозиция системы в рамках этой иерархии продолжается до тех

пор, пока на нижнем уровне не будут получены элементы

, принадлежащие

разработанным типам, или сформулированы технические задачи создания

необходимых элементов [82].

При применении каждого критерия в отдельных задачах, возникаю-

щих на рассматриваемом этапе разработки материала, определяются ха-

рактеризующие его количественные показатели, единицы и способы изме-

рения (расчетные, экспериментальные или экспертные оценки), альтерна-

тивой которым, естественно, являются лишь бездоказательные суждения о

качестве

системы.

Зависимости между критериями выявляются методами факторного

анализа и математической статистики и др., представляют эмпирические

закономерности или получаются на основе процедур оценки гипотез и

взвешивания факторов [83].

В соответствии с введенной иерархией критериев и выделенными

комплексами решаемых частных задач строится

иерархическая структура

системы – материала

−

с оценками её элементов, которая и служит осно-

вой перспективного планирования всего комплекса разработок и отдель-

ных систем.

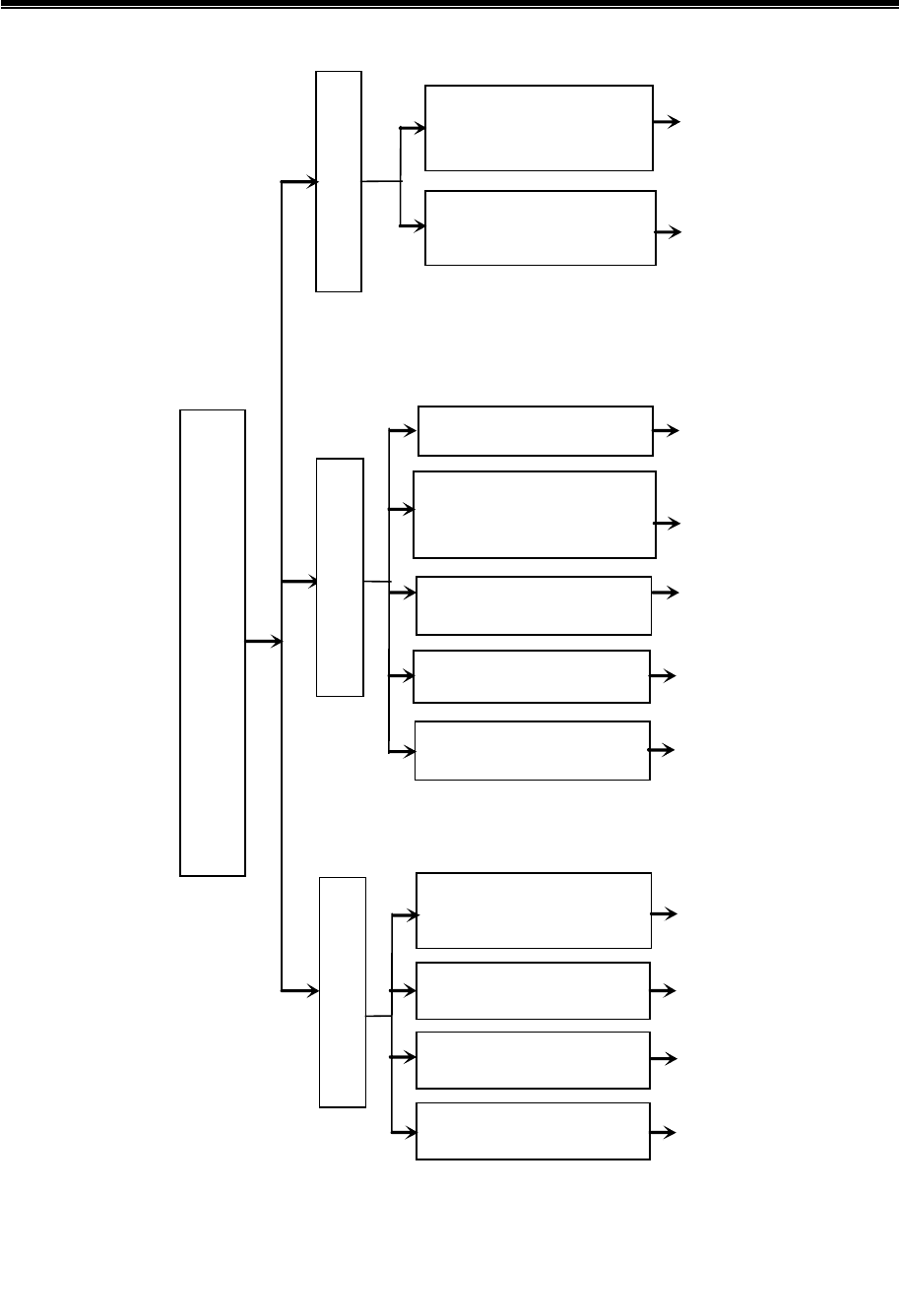
На рис. 2.3 приводится часть ее, относящаяся к структуре радиаци-

онно-защитного материала. При синтезе указанных систем, связанных с

выбором рецептуры, технологии и способов управления качеством, ис-

пользуются различные способы оптимизации параметров системы, в том

числе

векторной оптимизации.

С проблемой многокритериальности связана неопределенность це-

лей. Добиться одновременной оптимизации всех критериев невозможно в

принципе.

При синтезе материалов можно использовать следующие приводи-

мые ниже способы

преодоления неопределенности целей:

1) Линейная свертка.

Глава 2

КАЧЕСТВО СИСТЕМЫ

(радиационно-защитного

композита)

Характеристики

материала

Важность

Актуальность

Перспективность

Область применения

Помехозащищенность

Точность

Надежность

Чувствительность

Качество

управления

Совершенство

структуры

Сложность

Осуществимость

Ресурсы

Возможности

модификаций

Стоимости

Затраты

Защитные свойства

Физико-механические

свойства

Технологичность

Защита от

ионизирующих

излучений

Локализация

аварий

Изоляция отходов

АЭС, хранилища

Ремонт объектов

Субмикроструктура

Микроструктура

Макроструктура

Морозостойкость

Химстойкость

Термо-, тепло-,

огнестойкость

Смачиваемость

Адгезионное

взаимодействие

Радиационная

стойкость

Формуемость,

однородность

Прочность

Водопоглощение

Непроницаемость

Теплоемкость,

теплопроводность

Плотность

Коэф. накопления

Коэф. выведения

Коэф. ослабления

Когезионное

взаимодействие

Температура

кристаллизации

Температура

стеклования

Растворимость

компонентов

Степень

закристаллизо-

ванности

Температура

плавления

Природа

вещества

Дефектность

вещества

Долговечность

Скорость

химических

реакций

Фазовый состав

Термодинами-

ческие показа-

тели

Обучение персонала

Техническое

перевооружение

Энергозатраты

Производственные

затраты

Себестоимость

продукции

Себестоимость

ресурсов

Технология

Рецептура

Модификаторы

Заполнитель

Наполнитель

Вяжущее

Наличие сырья

Наличие технологии

Инновационные

технологии

Объекты

спецназначения

Защита населения

Купирование

отходов

Защита персонала

Структурные показатели

Физико-химические показатели

Топологические показатели

Взаимодействие

на границе раздела

фаз

Минералогический и

фазовый состав

Химические

свойства

Параметры

фазовых

переходов

Грануломет-

рический

состав

Пористость

Количество

фракций

заполнителя

Общая

пористость

Содержание

фракций

Крупность

заполнителя

Закрытая

пористость

Открытая

пористость

Полезность

системы

Качество

функционировани

Организация

системы

Эволюционная

эффективность

Экономическая

эффективность

IV уровень

V уровень

I уровень

II уровень

III уровень

Рис. 2.2. Иерархическая структура критериев качества радиационно-защитного

композита

Синтез композиционных материалов как задача управления

Макроструктура

Крупность заполнителя

Размер и концентрация

макропор, капиляров,

трещин, пустот

Субмикроструктура

Размер характерного

структурного элемента

Вид и концентрация

фазовых контактов и

дефектов

Структура

радиационно-защитного композита

Микроструктура

Дисперсность наполнителя

Размеры и концентрация

микротрещин, мезо-

и макропор

Толщина прослойки

связующего

I уровень

II уровень

Соотношение диаметров

зерен заполнителя

Высота рельефа

поверхности заполнителя

Толщина контактной зоны

Шероховатость

поверхности наполнителя

Рис. 2.3. Фрагмент иерархической структуры радиационно-защитного композита

Глава 2

Здесь используется один критерий

() ()

∑

fcF

xx , где f

– частные кри-

терии (например, характеристики кинетических процессов, наличие мест-

ных ресурсов, стоимость и т.д.);

– весовые константы (определяются в

результате экспертизы либо другими методами, например, на основе оцен-

ки корреляционных связей между обобщенным критерием

()

xF и частны-

ми критериями

(

)

f ).

2) Введение контрольных показателей

∗

, таких, как

()

niff

,1, =≥

∗

x ,

и выделение основного критерия

(

)

f (например, ограничения по стои-

мости, температурной и радиационной стойкости, энергопотреблению,

безопасности технологии и т.д.).

3) Построение множеств Парето.

При решении ряда частных задач

строились

множества Парето и сразу исключались те варианты решений,

которые заведомо плохи.

В большинстве случаев

целевая функция может определяться исходя

из желаемого вида

кинетических процессов формирования основных физи-

ко-механических характеристик композиционных строительных мате-

риалов

(прочность, модуль упругости, контракция и усадка, нарастание

внутренних напряжений, химическая стойкость, водопоглощение и водо-

стойкость и т.д.) на основе решения сначала общей, а затем частной задачи

идентификации. Такой выбор целевой функции, в частности, определялся

возможностью установления связи между строением композиционного

материала и проявляющимися при соответствующих условиях изменения-

ми макроскопических

характеристик [84].

Синтез композиционных материалов как задача управления

2.3. Принцип Парето в управлении качеством материала

Принцип Парето сформулирован Джураном

[71], состоит он в пред-

положении, что большая часть результатов вызывается относительно не-

большим числом причин. В основном принцип Парето используется для

анализа по специально построенным диаграммам возможных источников

брака с целью последующего совершенствования технологии производст-

ва. Применительно к технологии по принципу Парето «80 % потерь из-за

брака или переделок проистекает вследствие 20 %

причин». Точно так же

Парето обнаружил, что 80 % благосостояния контролируется 20 % людей.

И вообще, в количественной формулировке 80 % всех возникающих про-

блем происходит из-за 20 % причин (исходные материалы, уровень подго-

товки операторов, работа машин и т.д.)

Принцип Парето наглядно характеризует взаимоотношения «причи-

ны – результаты» в системе и является одним из наиболее используемых

инструментов

принятия решений. Однако авторам неизвестен случай его

использования при синтезе строительных материалов.

Ниже приводится пример использования диаграмм и принципа Па-

рето для

управления качеством по виду кинетических процессов формиро-

вания требуемых структуры и свойств эпоксидных композитов (ЭК) по-

вышенной плотности для защиты от радиации с использованием отходов

стекольной промышленности.

По Парето можно предполагать, что на-

чальные 20 % определяют последующие 80 % времени выхода контроли-

руемого параметра на эксплуатационное значение

При скалярном управлении

(

)

yt часто оптимизация осуществляется

на основе функционала:

() ()

[]

dttytyI

∫

β+α=

(2.7)

В частном случае при

α=1, β=0:

()

∫

dttyII

(2.8)

и оптимизация обеспечивает перевод объекта из начального в конечное со-

стояние на промежутке

[0,Т] с минимальной энергией управления.

Учитывая, что управление структурой и свойствами материала осу-

ществляется изменением соответствующих рецептурно-технологических

параметров, естественен подход к

синтезу материалов как к задаче

управления

. Воспользуемся этой аналогией при синтезе материалов.

Учитывая, что структура композита

в большей степени зависит от

скорости расхода энергии, чем от ее величины, сообщенной системе, для

кинетического процесса

()

xt наряду с I

рассмотрим функционал:

Глава 2

()

∫

dttxII

(2.9)

кумулятивную кривую

()

Как оказалось, для всех основных кинетических процессов

()

xt , t∈ [0, Т] выполняется условие:

(

)

(

)

TITI 8,02,0 ≥ , что подтверждает

возможность использования принципа Парето при оценке формирования

физико-механических характеристик материалов. А именно,

структура и

свойства

материала на 80 % определяются начальными 20 % длительно-

сти выхода контролируемого параметра на эксплуатационное значение.

Для иллюстрации на рис. 5.6 приводятся кинетические процессы

(

)

и соответствующие им кумулятивные кривые (1), (2) тепловыделения для

указанных ЭК.

Отметим также, что из сравнения кумулятивных кривых

(

)

(

)

следует, что

при использовании диаграмм Парето необходимо исходить из

функционала

(2.9).

Как подтвердили многочисленные исследования, применение прин-

ципа Парето значительно облегчает и разработку рецептуры (содержание

ингредиентов, гранулометрический состав и т.д.):

выделить элементы в

рецептуре, определяющие, в основном, эксплуатационные характеристи-

ки материала.

Для рассматриваемых ЭК прочность

и плотность, в основ-

ном, определяются степенью наполнения и видом модификатора. Эта за-

висимость для наглядности

условно представлена в виде поверхности и

приводится на рис. 5.22.

Очевидна возможность использования принципа Парето для итера-

тивного способа улучшения качества материала на основе последователь-

ного построения на каждом этапе соответствующих диаграмм Парето.

Синтез композиционных материалов как задача управления

2.4. Теоретические аспекты планирования эксперимента

Синтез материалов в большинстве случаев может быть произведен

лишь на основе синтетического теоретико-экспериментального метода.

Важную роль при этом играет установление необходимой степени форма-

лизации задачи, а также организации эксперимента.

Сталкиваясь с многокритериальными задачами строительного мате-

риаловедения, естественно попытаться найти способы сведения их к зада-

чам с одним критерием, поскольку

для однокритериальных задач сущест-

вуют хорошо разработанные методы решения. Эти способы носят нефор-

мальный характер, ибо они не могут быть получены как результат решения

какой-либо математической задачи. К ним, в частности, относятся линей-

ная свертка критериев, выделение приоритетного критерия и др.

Но к анализу многокритериальных задач можно подойти и с

других

позиций: попытаться сократить множество исходных вариантов

, т.е. ис-

ключить из неформального анализа те варианты решений, которые заве-

домо будут плохи.

Один из подобных путей, предложенный итальянским

экономистом В. Парето еще в 1904 г., в частности, уже использовался ав-

торами для определения оптимальной рецептуры материала с повышен-

ными защитными свойствами от воздействий ионизирующих излучений.

Пусть сделан некоторый выбор. Обозначим его через

x∗ и предпо-

ложим, что существует некоторый другой выбор

такой, что для всех

критериев

()

f имеют место неравенства:

()

(

)

niff

,1,xx

=≥ ,

(2.10)

причём хотя бы одно из неравенств – строгое.

Очевидно, что выбор

предпочтительнее x∗. Поэтому все векторы

x∗

, удовлетворяющие (2.10), можно сразу исключить из рассмотрения.

Имеет смысл заниматься сопоставлением и подвергать неформальному

анализу только те векторы

x∗, для которых не существует x

такого, что

для всех критериев удовлетворяются неравенства (2.10). Множество всех

таких значений

x∗ называют множеством Парето, а вектор x∗ называют

не улучшаемым вектором результатов (вектором Парето)

, если из

()

(

)

ff ≥ для любого i следует

(

)

(

)

ff = .

Если цели являются двумя

однозначными функциями

(

()

(

)

maxmax,

→→ xx ff ), то каждому допустимому значению перемен-

ной

x отвечает одна точка на плоскости (f

, f

) (рис. 2.2), и равенства

() ()

2211

, ffff == определяют параметрическое задание некоторой

кривой

abcd в этой плоскости. Участок bc, очевидно, не принадлежит

множеству Парето, поскольку вместе с ростом

происходит и рост f

. Та-

ким образом, на этом участке изменению переменной

x отвечает одновре-

менное увеличение обеих целевых функций и, следовательно, такие вари-

Глава 2

анты решений должны быть сразу исключены из дальнейшего рассмотре-

ния.

Рис. 2.4. Выбор допустимых значений

В теории принятия решений существует термин “принцип Парето”,

заключающийся в том, что выбирать в качестве решения следует только

тот вектор

x, который принадлежит множеству Парето. Принцип Парето

не выделяет единственного решения, он только сужает множество аль-

тернатив

. Окончательный выбор остаётся за лицом, принимающим реше-

ние. Построение множества Парето облегчает процедуру выбора решения.

Помимо критериев

()

f , достаточно часто можно вводить некото-

рый общий критерий

F (x). Иногда его можно формализовать и записать в

явном виде. В этом случае исследователь имеет возможность решить

задачу до конца. Для этого достаточно определить вектор

x, который дает

решение задачи:

(

)

max→xF при

(

)

fffP ,,,

∈

x , где

()

Pff f

Gn12

,,,K

– множество Парето для функций

ff f

n12

,,,K на множестве G допусти-

мых векторов

x. Введение “общего” (глобального) критерия

()

xF и макси-

мизация его значений на множестве Парето является некоторой гипотезой,

поскольку из совокупности критериев

ff f

n12

,,,K , F один из критериев

специальным образом выделяется.

Как видим, приближённое

построение множества Парето относит-

ся к числу очень важных и трудных задач численного анализа, но, к сожа-

лению, до самого последнего времени обделенных вниманием.

Рассмотрим случай двух критериев. Пусть ищется решение задачи:

() ()

Gff

∈

→→ xxx max,max,

(2.11)

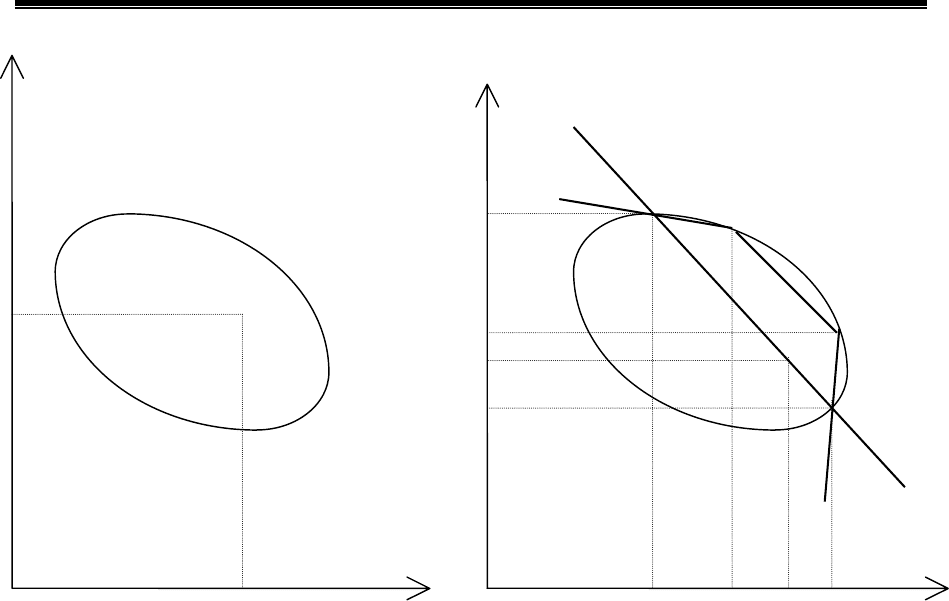
Синтез композиционных материалов как задача управления

Рис. 2.5. Построение множества Парето

Каждой точке

∈

x соотношения

(

)()

2211

, ffff ==

(2.12)

ставят в соответствие некоторую точку

f ∈ G

в плоскости критериев

(рис. 2.3). Соотношения (2.12) определяют отображение множества

на

Множество

носит название множества достижимости или

множества предельных возможностей.

Множество Парето представляет

собой границы

. На рис. 2.5 множеством Парето будет дуга АDCВ.

Приближённое построение множества Парето сводится к последо-

вательному решению задач математического программирования.

Опишем

одну из

возможных схем расчёта. Зафиксируем желательные значения

критериев

и f

: f

= c

, f

= c

Значения c

и c

должны принадлежать множеству достижимо-

сти.

Решив две оптимизационные задачи:

()

max

→xf , II.

(

)

max

→xf ,

(

)

, cfG

=∈ xx ;

()

, cfG

∈

xx ,

определим точки

А и В (рис. 2.5). Проведя через них прямую 1, получим

простейшую

аппроксимацию множества Парето. Для уточнения послед-

Глава 2

него можно определить ещё две точки – C и D, принадлежащие этому

множеству и соответствующие решениям нижеследующих задач:

III.

()

max

→xf , IV.

(

)

max

→xf ,

(

)

, cfG

=∈ xx

;

()

, cfG

∈

xx .

Значения

и c

также должны принадлежать множеству достижи-

мости. Ломаная

ADCB будет следующим приближением множества Паре-

то.

При

dxcbxa

≤

()

(

)

2211021222110211

,,, xxxxfxxxxf β+

≈

α+α≈

построение множества Парето сводится к последовательному решению

двух задач

линейного программирования.

1. Определить неотрицательные значения

,, доставляющие мак-

симум целевой функции

()

22110211

, xxxxf

при ограничениях:

;,,,

222110

2211

cxx

dxcxbxax

=β+β+β

≤

≥

≤

≥

2. Определить неотрицательные значения

,, доставляющие мак-

симум целевой функции

()

22110212

, xxxxf

при ограничениях

;,,,

122110

2211

cxx

dxcxbxax

=α+α+α

≤

≥

≤

≥