Bolotin Y., Tur A., Yanovsky V. Chaos: Concepts, Control and Constructive Use

Подождите немного. Документ загружается.

34 3 Main Features of Chaotic Systems

(

)



(

)

(

x − f

(

))

dy. (3.32)

In other words, the invariant distribution function does not change at phase space

transformations by the phase ﬂow (or by the mapping) (3.26). Naturally, it satisﬁes

[as well as P

(x)] the normalization condition



(

)

dx = 1 .

It should be stressed that the introduction of the invariant density is based on the

relaxation of the initial density in relation to the invariant one. There arises an impor-

tant question: in what systems, or more precisely, in systems with what properties

will such relaxation take place? Discussion of this question requires that we touch

on the question of the foundations of statistical mechanics, ergodicity, and measure

theory [34]. We will return to them in another section. Besides this, introduction of

the distribution density is not justiﬁed for all dynamical laws. There are situations

when it is impossible to extract the density from the measure, and in such dynamical

systems singular or multi-fractal measures appear. The examples will be considered

further.

Example 3.3. Let us now consider a simple example of invariant density calculation

for tent mapping. The functional Frobenius–Peron Eq. (3.28) in that case takes the

form

(

)





+ P



1 −



It is easy to ﬁnd a particular solution of that equation P

(

)

= 1. This solution is

realized at r = 1 and it corresponds to uniform distribution. At other values of r > 1

the situation, as well as the invariant density form, is less insigniﬁcant.

For dynamical systems under conditions of ergodicity the Lyapunov exponent

can be calculated from the invariant density distribution in the following way

λ =



(

)





(

)



dx ≡











The invariant density permits us to calculate also the mean-square ﬂuctuations λ

Δλ













−













In some cases this is sufﬁciently efﬁcient.

Chapter 4

Reconstruction of Dynamical Systems

The concept of attractors plays an important role in physical research. This is

because of their prevalence. Aside from that, when investigating properties of

dynamical systems, we are actually studying attractors. In a certain sense, attractors

realize the dynamical variant of the statistical principle of shortened description.

Indeed, it is not necessary to study the behavior of a system in detail, starting from

initial conditions, if after a time the system will reach a stationary regime corre-

sponding to motion on the attractor. It is these limit regimes which must ﬁrst of all

be investigated. The existence and prevalence of such regimes is also important to

reconstruct or restore the properties of dynamical systems from experimental data.

Modern progress in that direction is to a great extent connected with the conception

of attractors. In fact, one of the central problems in physics is the creation of models

for the description of real physical phenomena. In many cases, those phenomena

are so complicated that it is not always clear what physical principles lie at their

root. This is especially clearly seen in attempts to describe various phenomena in

biological systems. On the other hand, experimental investigations do not and can-

not give exhaustive or complete information on real systems. Therefore, it becomes

important to study the following problem.

4.1 What Is Reconstruction?

Let us consider a classical physical system about which we know very little or noth-

ing at all. Usually, it is called a black-box in order to stress our ignorance about the

system. The temporal behavior of this black-box is determined by the variation of its

generalized coordinates, which are all the parameters that determine the black-box

state. There can be many such parameters; the exact number is also unknown. It

is evident that experimental monitoring of all those generalized coordinates is a

hopeless task. It was earlier believed that only in such hopeless cases could reliable

information on the classical (nonquantum) system be obtained. A more realistic

task is the experimental measurement of the evolution of one parameter over time.

A question arises: what can we know about the properties of the black-box from

such incomplete experimental information? Of course, we must nevertheless rely

Y. Bolotin et al., Chaos:Concepts, Control and Constructive Use, Understanding

Complex Systems, DOI 10.1007/978-3-642-00937-2



Springer-Verlag Berlin Heidelberg 2009

36 4 Reconstruction of Dynamical Systems

on some assumptions. Thus, we will assume that the system is nonlinear and dis-

sipative; this will be the most complex and interesting example. We can therefore

expect that the black-box is in a stationary regime corresponding to some attrac-

tor. Our measurements can conﬁrm or refute this, if, for example, our black-box

explodes. The very presence of an attractor is already an important fact that allows

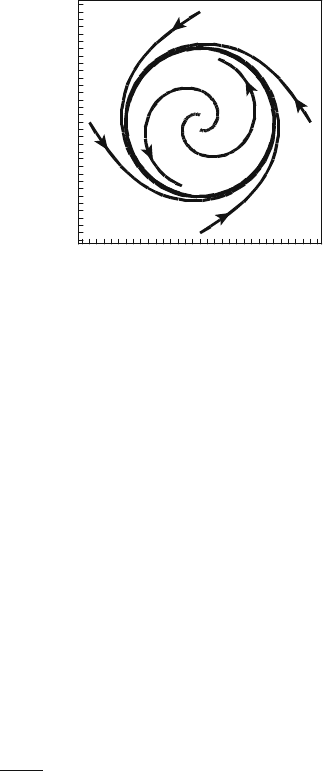
us to advance further. Let us begin with a simple and well-known example: a very

simple attractor known as the limit cycle (see Fig. 4.1).

Fig. 4.1 Phase portrait with

limit cycle

0.5

–0.5

–1

–1.5

10.50–0.5–1–1.5

x(t)

y(t)

Example 4.1. In this example we will try to understand a basic idea that can also

be applied in more complicated cases. Let the limit cycle be determined by the

parametric equations

x = a sin(ωt)

y = a cos(ωt) .

(4.1)

This means that it coincides with a circle of the radius a centered in the origin. From

the gedanken experiment we extract only the temporal variation of the coordinate

x = x(t) = a sin(ωt). However, in the process of evolution the system visited all

the attractor points. Therefore, this coordinate contains information about the entire

attractor. The question is only how to extract it. Let us construct a vector x according

to the following rule

x = (x

(t), x

(t)) = (x(t), x(t + τ )) . (4.2)

Let us assume now that τ is small and transform the vector to the following form

x =



x(t),

∂x(t)

∂t



. (4.3)

Using the explicit form of x = x(t), it is easy to rewrite it in the form

x = (x

(t), x

(t)) = (x(t), y(t)τ · ω) .

4.1 What Is Reconstruction? 37

After the choice τ =

we obtain the vector exactly running through the original

limit cycle.

In some sense, we reconstructed the whole attractor from only one known coordi-

nate. In the above procedure only the choice of τ required some additional informa-

tion about the attractor. All the other steps were executed using only the assumed

experimental data on the temporal variation of the ﬁrst coordinate. The choice of τ

could be grounded independently by the following “principle.” Characteristic scales

on both axes of the attractor coincide or are very close. This concept is also very

often used in more complex cases. Of course we knew in advance the dimension

of the space where the limit cycle was situated, and limited ourselves to the two-

dimensional vector. The presented considerations are qualitative. At ﬁrst sight they

appeared to be efﬁcient because of the speciﬁc form of the attractor, but this is not

quite so. To illustrate, let us consider a system of nonlinear equations.

= A(x

, x

)

= B(x

, x

)

= C(x

, x

) .

Time-differentiating the ﬁrst equation and using the two other equations to eliminate

the derivatives

and

, we obtain the following equations

= A(x

, x

)

= D



, x



Let us assume that we are able to solve that system of equations with respect to x

and x

= G





= R





From those relations, it follows that in principle, it is possible to determine the tem-

poral variation of the coordinates x

and x

when given the variation x

(t),

(t)

and

. In other words, from data for x

(t) and, accordingly, x

(t+τ ), x

(t+2τ ), we can

reconstruct the coordinates x

and x

. Therefore, the possibility of reconstructing

the attractor from information on the temporal variation of one coordinate exists in

more complex cases as well.

38 4 Reconstruction of Dynamical Systems

The idea of reconstructing the phase portrait in multi-dimensional dynamical

systems from the temporal dependence of one coordinate was ﬁrst expressed in

[35]. The method of introducing a vector to determine the system’s position in n–

dimensional phase space is absolutely analogous

ξ =

(

x(t), x(t +τ ),...,x(t + (n − 1) ·τ )

)

, (4.4)

where τ, 2τ,...,

(

n − 1

)

τ are called time delays. This vector evolves in time and

draws the trajectory in n dimensional phase space. Then, the problem is in deter-

mining the dimension n of the phase space.

4.2 Embedding Dimension

Before discussing embedding dimension let us recall what is understood as mani-

fold embedding in space. Let the space dimension or X manifold be smaller than

the space dimension Y .Ifthemap f : X → Y , gives one-to-one correspondence

between points X and f (X) then the Jacobian rank

∂ f

∂x

is everywhere equal to the

manifold dimension X dim X, and is called the embedding of X in Y . For instance,

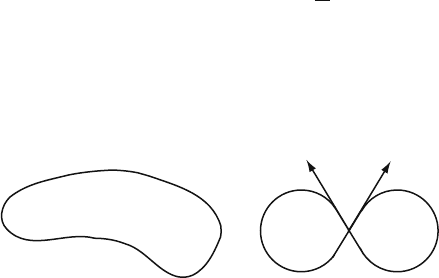
the embedding of a circle into bidimensional space is shown on Fig. 4.2 at the left.

Mapping f : X → Y which does not need one-to-one correspondence is called

immersion. To put this another way, immersion is an embedding but is only local.

Figure 4.2 at right shows an example of the immersion of a circle into R

Fig. 4.2 At left is the embedding of the circle S

→ R

.Attheright is only its immersion into R

In this last case each vector of velocity on the circle corresponds to the unique velocity vector on

the ﬁgure-eight. But there is no one-to-one correspondence between the points of the image and of

the prototype

In the previous example the dimension of the space where the attractor was

embedded was known. There were two important topological characteristics: the

dimension of the attractor and the dimension of the space (manifold) to which the

attractor belongs. Of course, these characteristics cannot take arbitrary values inde-

pendently. For instance, the attractors dimensions cannot exceed the dimensions of

the embedding space. The dimensions of the space where the attractor is embedded

are important since they determine the minimum number of nonlinear equations

which describe the attractor in this phase space. Let us assume that the attractor

belongs to a D-dimensional manifold. Then we can use Whitney’s theorem (see for

example, [36–39]), providing that any D-dimensional manifold can be embedded

into Euclidean space R

2D+1

4.2 Embedding Dimension 39

There is a simple way to understand Whitney’s theorem. To obtain the one-

to-one correspondence of image and prototype we need to set D coordinates. In

order to have the same correspondence between the tangent vectors we also have to

set another coordinate D. And ﬁnally, we have to add another coordinate to avoid

self-intersection as shown on Fig. 4.2. Thus, the D -dimensional manifold can be

embedded into space with the dimension n = 2D + 1. Now, we have to be sure

that there are nonintersection points. Let us consider the condition providing the

absence of intersection points of two hypersurfaces in space R

. Let us deﬁne the

hypersurface of D dimension by the equations

(

, x

, ..., x

)

= 0 .

The number of these equations is n − D. Therefore i = 1, 2, ...n −D. Let us deﬁne

the second hypersurface of D dimension by the equations

(

, x

, ..., x

)

= 0 .

Where i = 1, 2, ...n − D. The choice of the same dimension of hypersurfaces is

suitable for the analysis of intersection points as well. The total number of equations

is 2n − 2D, while the number of unknown coordinates is n. It is clear that if 2D =

n, then the number of equations is equal to the number of unknown coordinates.

That means that in general cases, these equations have a ﬁnite number of solutions

which determine the coordinates of a ﬁnite number of intersection points for these

hypersurfaces. If 2D < n − 1 then the number of equations is bigger than the

number of unknown coordinates. Hence, there is no solution of this kind of equation

in general cases. It means that if

n > 2D + 1 ,

there are no intersection of these hypersurfaces. Now it is evident that this dimension

limitation corresponds with Whitney’s theorem.

Whitney also proved the enhanced version of the embedding theorem [36].

According to this theorem every paracompact D, or dimensional Hausdorff man-

ifold, is embedded into R

space.

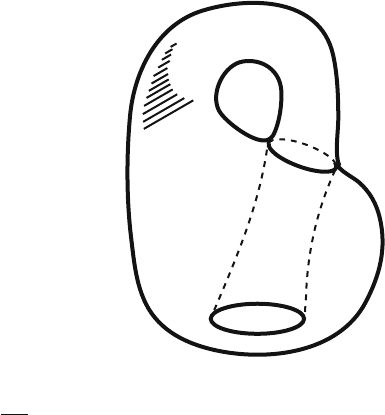
Example 4.2. Notice that there are some bidimensional manifolds which cannot be

embedded into three-dimensional Euclidean space, R

. This follows from Whitney’s

theorem. The best-known example of such a manifold is the Klein bottle. Figure 4.3

shows its model in R

with self-intersections. However, without self-intersections-

Klein bottle can be embedded into four the dimensional Euclidean space. This cor-

responds fully to Whitney’s enhanced theorem.

Theoretical progress followed this direction. In 1981, Takens [40] was able to

prove the theorem, which immediately attracted much attention. Its content can be

explained in the following way. Let a system of equations, in phase space of which

an attractor exists, be the following

40 4 Reconstruction of Dynamical Systems

Fig. 4.3 This ﬁgure shows

one side surface of the Klein

bottle

= F

(x) ,

where i = 1,...,n. Then in 2D + 1–dimensional space

ξ =

(

x(t), x(t +τ ),...,x(t + 2D · τ )

)

, (4.5)

there is another attractor, all the metric properties of which coincide with the ones of

the original attractor. The dimension of that space is D

 (2D +1) and it is called

the embedding dimension (see also [41]). The sign of inequality means that if the

attractor can be embedded into a space of some dimension, then it can be embedded

into spaces of higher dimensions.

Generalization of Whitney’s theorem for a case with a fractal image which is

consequently not a manifold is done in [41]. In this example it was proved that the

manifold A can be embedded into dimension space n providing

n  2D

+1 .

Where D

is the capacity of compact set A. Later we discuss this and other dimen-

sions in detail. In fact, instead of x(t) we can take any coordinate from the original

system. In spite of the limitations and idealized character of that theorem, it was

immediately utilized in the reconstruction of attractors and their properties in many

physical systems. First, we suppose that temporal series are measured with absolute

precision on the inﬁnite time interval. In addition, we suppose that there are no

noises at all which can inﬂuence the system. In spite of this extreme idealization

Takens theorem is broadly used to restitute attractors in phase space as well as

to ﬁnd its dimension, Lyapunov Index, topological entropy, and other important

characteristics of dynamical systems. A generalization of this theorem for systems

with external forces, including stochastic ones, was also obtained in [42]. However,

4.3 Attractor Dimension 41

in order to really utilize that theorem or its generalizations one needs to learn to

determine either the attractor dimension or the embedding space dimension from

one-dimensional signal data.

4.3 Attractor Dimension

Let us turn now to a discussion of the dimension of attractors. In the case of an

attractor like the one in the example above, there is no difﬁculty in determining

its dimension. The limit cycle itself represents a manifold which is topologically

equivalent to a circle S

. However, it is well-known that attractors can be of dif-

ferent natures, and they can also be nonmanifold. This is one of the impressive

discoveries at the heart of modern theory on dynamical systems. In other words,

there are stationary regimes distinct from constants (where the attractor is a stable

ﬁxed point) and from periodic ones (where the attractor is a limit cycle or a limit

torus). The appearance of such new stationary regimes strongly affected views on

many physical processes. A widely known Ruel and Takens scenario [43] of turbu-

lence origination is also based on the concept of strange attractors. They are called

strange due to their unusual geometrical properties. Stationary regimes of dynamical

system motion on strange attractors are chaotic. The strange attractors are already

not manifolds and they are arranged in quite a complicated way. In modern terms,

we can say that in some directions they appear to be fractals like the Cantor set. It is

clear that the dimensions of such objects deserve more detailed discussion.

The Hausdorff dimension is named after the man who invented one of the main

ways of determining dimensions for fractal sets [44]. First, to introduce the Haus-

dorff measure. Let us cover our object X in spheres A

of radius δ(A

) that do not

exceed radius ε, so that every point of X will belong to one of the coverage spheres.

Now we consider the sum

= inf

∞



i=1

(

)

where inf is the lower boundary over all coverages and p ∈ R is an arbitrary real

parameter. Then the following

(

)

= sup

ε>0

(

)

is called the p-dimensional Hausdorff measure. This measure as the function of p

has a remarkable property. It looks like a special step: at small p it goes to inﬁnity,

and at large ones it is 0 (see Fig. 4.4).

Number D,forwhichm

(

)

= 0forp > D and m

(

)

=∞for p < D,is

called the Hausdorff dimension of the set X. It means:

dim

X = D .

42 4 Reconstruction of Dynamical Systems

Fig. 4.4 Shows symbolically

the dependence of the

Hausdorff measure m

value p

It is important to note that the Hausdorff dimension is not necessarily an integer and

therefore it is a very useful tool for the analysis of the structure and complexity of

different sets.

If we introduce N

(

)

as the minimum number of p-dimensional cubes of side ε

needed to cover the set, then their capacity can be deﬁned as,

dim

X = lim

ε→0



−

logN

(

)

logε



, (4.6)

where ε tends to zero. The capacity of a set was originally deﬁned by Kolmogorov

[45] (also called the box-counting dimensional). The Hausdorff dimension and the

capacity require only a metric (i.e., a concept of distance) for their deﬁnition, and

consequently we refer to them as “metric dimensions.” The value of capacity coin-

cides with fractal dimension.

Let us consider some examples of sets which have different dimensions. We start

from an ordinary square Q. It is evident that its usual (topological) dimension equals

2. Let us now determine its Hausdorff dimension. First of all we cover the square Q

with the same quadratic neighborhood of dimensionless size ε. In this case it is easy

to calculate the sum m

(

)



= N

(

)

Where N

(

)

is the number of square neighborhoods of size ε, covering the square

Q (see Fig. 4.5). The number of such squares (see Fig. 4.5) is

Fig. 4.5 Coverage of a square

by square neighborhoods of

size ε, the number of which is

(

)

= ε

−2

4.3 Attractor Dimension 43

(

)

= ε

−2

After substitution into the previous equation we obtain

(

)

= ε

p−2

To estimate the Hausdorff measure we need to use the limit ε → 0. It is clear that

when p > 2thesumm

is proportional to the positive power of ε and correspond-

ingly this sum limit is equal to zero. Hence, the Hausdorff measure with p > 2is

equal to zero. When p < 2thesumm

(

)

is proportional to the negative power of

ε and the limit m

(

)

is going to inﬁnity. Thus, we obtain by deﬁnition

dim

Q = 2 .

It is easy to see that in this case (as well as for other “normal” sets) the Hausdorff

dimension coincides with the usual (topological) dimension. Let us now consider a

more exotic example in a Cantor set K . This set is built by the iterative procedure,

which implies dividing the interval, obtained in the preceding step of the iteration,

by 3 and consecutively removing the central part. Several steps of this process are

shown in Fig. 4.6. We can see that after n steps of construction the set consists of

= 2

intervals whose length is ε

= 3

−n

. For the limit case the Cantor set

consists of points with the coordinates

x =

+····

+···,

where a

coincides either with 0 or with 2. Let us now determine its Hausdorff

measure. For that we cover it on n - step of construction with intervals of ε

= 3

−n

length and we calculate the sum m

(

)

. For a set like this, it is easy to ﬁnd m

(

)

at each iteration step

(K ) = Σε

= N

The number of segments which covers it on n - step, is also easy to calculate as

(

)

= 2

. Now we can write N

(

)

as a function of ε

using some simple

transformations

(

)

= 2

= e

−n ln 2

= e

−n

ln 2

ln 3



−n ln 3



ln 2

ln 3

(

)

ln 2

ln 3

and we obtain

(

)

(

)

ln 2

ln 3

As a result, for the sum m

(

)

we have