Богословский С.В. Дорофеев А.Д. Динамика полета летательных аппаратов
Подождите немного. Документ загружается.

11
2. СТАТИЧЕСКАЯ УСТОЙЧИВО СТЬ И СТАТИЧЕСКАЯ
УПРАВЛЯЕМОСТЬ ЛЕТАТЕЛЬНОГО АППАРАТА
2.1. Аэродинамические силы и моменты,
действующие на летательный аппарат в полете
Системы координат
Вторые производные от линейных и угловых координат, стоящие в
левой части уравнений системы (10), используются при изучении ди-
намики для моделирования сил инерции , возникающих при ускорен-
ном движении ЛА. При изучении статики вторые производные полага-
ются равными нулю.
Система уравнений (10) в общем случае дополняется уравнениями,
устанавливающими соответствие между различными системами коор-
динат, которые были использованы при про ектировании сил и момен-
тов, а также уравнениями, дополняющими систему (10) до замкнутой
системы уравнений. Например, если учитываются силы и моменты, со-
здаваемые органами управления в зависимости от изменяющихся ли-
нейных и угловых координат ЛА, систему уравнений необходимо до-
полнить уравнениями контуров измерения координат и уравнениями
контуров управления.
Первая группа уравнений системы (10) отражает движение центра
масс, а вторая – движение вокруг центра масс ЛА.
Как следует из рассмотрения системы (10), для изучения особеннос-
тей движения ЛА необходимо составить математические модели сил и
моментов, действующих на ЛА. Такие модели должны отражать зави-
симость действующих на ЛА сил и моментов от конструктивных пара-
метров и от параметров законов управления ЛА.
Движение ЛА моделируется обычно в нескольких системах коорди-
нат (земной, связанной, скоростной, нормальной), выбираемых иссле-
дователем при постановке задачи.

12
Оси и начало координат нормальной земной системы координат
(OX
g
Y
g
Z
g
) связаны с выбранной точкой на земной поверхности и с на-
правлением местной вертикали.
Оси нормальной системы координат (OX
g
Y
g
Z
g
) имеют то же направ-
ление, что и оси нормальной земной системы координат, но начало ко-
ординат размещается в центре масс ЛА.
Продольная и нормальная оси и начало координат связанной систе-
мы координат (OXYZ) расположены в пло скости продольной симмет-
рии ЛА; продольная ось OX направлена вперед, нормальная – к верхней
части ЛА, поперечная – к правой части ЛА перпендикулярно к плоско-
сти симметрии; нача ло координат обычно помещают в центр масс ЛА.
Оси и начало координат скоростной системы координат (OX
а
Y
а
Z
а
)
связаны с положением вектора скорости центра масс ЛА; при этом на-
правление скоростной оси OX
а
совпадает с направлением скорости ЛА,
ось подъемной силы OY
а
лежит в плоскости продольной симметрии ЛА
и направлена к верхней его части, боковая ось OZ
а
направлена в сторо-
ну правого борта ЛА.
Силы, действующие на ЛА в полете
1. Сила тяжести. Если пренебречь кривизной и вращением Земли,
сила тяжести G равна гравитационной силе и направлена вертикально
вниз; ее проекции на оси связанной системы координат
sin ; cos cos ; cos sin
xy z
GG GG GG=− ϑ =− ϑ γ =− ϑ γ
.
2. Аэро динамические силы. Это силы, вызываемые взаимодействием
между атмосферой и движущимся в ней ЛА. Главный вект ор аэродинами-
ческих сил называется аэродинамической силой планера, обозначается R
A
и направлен в сторону, противополо жную скорости. Его проекции на оси
скоростной системы координат: X
a
– сила лобовог о сопротивления; Y
a
–
аэро динамическая подъемная сила; Z
a
– аэро динамическая бок ов ая сила.
Проекции R
A
на оси связанной системы координа т называются, соответ-
ственно, аэро динамическ ой про дольной силой, аэродинамическ ой нормаль-
ной силой и аэродинамической поперечной силой.
Каждой из этих проекций ставит ся в соответствие коэффициент про-
порциональности, например для скоростной системы координат
a
a
,
у
Y
с
qS
=

13
где
2
V
q
ρ
=
– скоро стной напор; S – характерная площадь ЛА (напри-
мер, площадь крыла).
3. Сила тяги. Сила тяги P – это главный вектор системы сил, дей-
ствующих на ЛА со стороны двигателя в результ ате его функциониро-
вания. Ее проекции на оси связанной системы координат
рр
cos ; sin .
xy
PP PP=ϕ =ϕ
2.2. Продольное движение лет ательного аппарат а
Моменты аэродинамиче ских сил,
к оторые действуют на летательный аппарат в продольном движении
При движении ЛА в а тмосфере в общем случае на него действуют аэро-
динамические силы, создающие моменты относительно трех осей OX, OY,
OZ и зависящие от режима: ск орости V, высоты полета Н, поло ж ения уп-
равляющих плоскостей (δ
н
, δ
в
– углы и
нв
,δδ
""
– угловые скорости отклоне-
ния рулей направления и высоты; δ
э
– углы отклонения элеронов).
Главный момент всех аэродинамических сил M определяется ка к
момент главного вектора аэродинамических сил относительно центра
масс. Проекции главного момента на оси связанной системы координат
имеют названия: проекция на ось OX (M
x
) – аэродинамиче ский момент
крена; проекция на ось OY (M
y
) – аэродинамический момент рыскания;
проекция на ось OZ (M
z
) – аэродинамический момент тангажа. Каждой
из этих про екций ставит ся в соответствие ко эффициент пропорцио-
нальности, например для аэродинамического момента тангажа
,
zzA
M m qSb
=
где b
A
– средняя аэродинамическая хорда (САХ), характерный размер
ЛА при определении параметров продольного движения.
Под средней аэродинамической хордой крыла произвольной формы
в плане понимают хорду равновеликого прямоугольного крыла, момен-
тные характеристики которого совпадают с моментными характеристи-
ками данного крыла.
Общее выражение для момента тангажа
Рез ультир ующий момент M
R
определяется аэродинамическим момен-
том M и моментом от тяги двигателя M
P
:
14
M
R
= M + M
P
.
При постоянной высоте и скорости полета и небольших значениях
кинематических параметров можно считать, что аэродинамиче ский мо-
мент тангажа зависит от них линейно. Расчеты и экспериментальные
данные показывают, что при малых значениях кинематических пара-
метров коэффициент момента тангажа ЛА можно представить следую-
щей зависимостью:
вв
0
вв
,
z
zzzz zz zz
mmmm mm m
δδω
αα
=+α+δ+α+δ+ω
"
"
"
"
где
в
в
;;
zA A A
z
bb b
VV V
ωαδ
ω= α= δ=
"
"
"
"
;
0
z
m
– ко эффициент момента танга-
жа при
вв
0
z
α=δ =α=δ =ω =
"
"
, зависящий только от конструктивных
параметров, формы летательного аппарат а и продольного момента, со-
здаваемого двигателем.
Величины
в
,
zz
mm
δ
α
называются статическими производными коэф-
фициента продольного момента,
в
,,
z
zz z
mm m
δω
α
"
"
– вращательными произ-
водными коэффициента продольного момента.
В том случае, когда отсутствует вращение ЛА относительно центра
тяжести (
в
0
z
α=δ =ω =
"
"
), выражение для продольного момента приво-
дится к виду
в
0
в
.
zz z z
mm m m
δ
α
=+α+δ
С достаточным приближ ением можно считать, что продо льный момент
ЛА состоит из продо льног о момента фюзеляжа, крыльев, оперения и из
про дольног о момента, соз даваемого двигателем . До на чала расчетов коэф-
фициент момента тангажа определяю т при испытаниях модели ЛА и от-
дельных ег о элементов в аэродинамической трубе. При этом указыв аю т
поло ж ение той точки, относительно которой определялся аэродинамичес-
кий момент тангажа. Обычно считают, что в этой точке с к оор динатами
(x
T
, y
T
) располо ж ен центр масс ЛА. К оординаты центра масс представляют
в относительных величинах (
;
TT
TT
AA
xy
xy
bb
==
, в долях или в процентах
САХ), в системе осей, начало к от орых О помещено в носк е САХ, ось ОХ
направлена вдоль этой хорды назад, а ось OY – перпендику лярно САХ и
вверх по отношению к ЛА.
15
Продольный момент, создаваемый фюзеляжем, сравнительно неве-
лик и определяется соотношением
ффф ф
(),
zdT
MYxx=−
где Y
ф
– по дъемная сила, создаваемая фюзеляжем;
фd
x
– коор дината цент-
ра давления фюзеляжа, отсчитыв аем ая от носовой оконечности ЛА;
фT
x
–
координата центра тяжести фюзеляжа.
Продольный момент крыла приближенно может быть определен как
произведение величины подъемной силы крыла на абсциссу центра дав-
ления
крd
x
относительно центра тяжести ЛА
кр
кр кр
().
zdT
MYxx=−
Используя соотношения для продольного момента подъемной силы
относительно его передней кромки, полученное выражение для m
z
кр
,
можно привести к виду
кр 0
(),
zmyTF
mCCxx=+ −
где
F
F
A
x
x
b
=
– относительная координата фокуса крыла (или линии фо-
кусов), который представляет собой точку приложения части подъем-
ной силы (для крыла с несиммет ричным профилем), обусловленной уг-
лом атаки;
0
m
C
– коэффициент момента крыла при α = 0. Если продиф-
ференцировать последнее выражение по C
y
, то можно получить стати-
ческую производную
кр
().
y
C
TF
z
mxx
=−
В общем случае вектор тяги двигателя Р может не проходить через
центр тяжести ЛА. В этом случае при работе двигателя будет возникать
дополнительный продольный момент (рис. 1)
дв
p
,
z
MPY=−
где Y
р
– расстояние между направлением вектора тяги двигателя и
центром тяжести ЛА.
При повороте руля или стабилизатора создается дополнительная
подъемная сила и дополнительный момент отно сительно цент ра тя-
жести ЛА. Продольный момент, создаваемый подъемной силой гори-
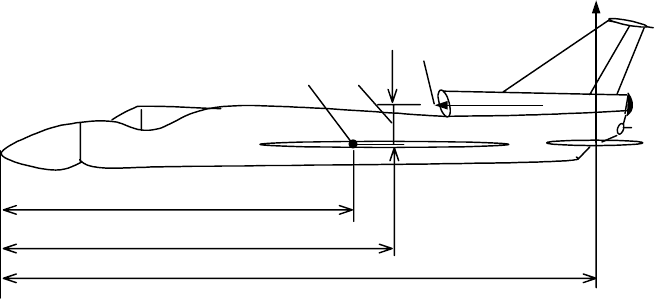
16
зонта льного оперения Y
г.о
, приложенной в центре давления с коор-
динатой x
dг.о
, для обычной классической аэродинамиче ской схемы
ЛА (рис. 1) можно записать
г.о
г.ог.о
().
zTd
MYxx=−
Рассмотренные моменты т ангажа, действующие на элементы ЛА,
могут быть условно разделены на три группы:
1. Моменты, зависящие от конструктивных параметров ЛА (момен-
ты крыла, фюзеляжа и горизонтального оперения при нулевом угле ата-
ки и нулевом положении руля высоты, момент от тяги двигателя). Сум-
ма всех этих составляющих продольного момента, или ко эффициента
момент а, обозначается
0
z
M
, или
0
z
m
.
2. Моменты, зависящие от угла атаки ЛА (моменты крыла, фюзеля-
жа, горизонтального оперения). Сумма этих моментов (или соответству-
ющий коэффициент момента) обозначает ся
z
M
α
α
, или
z
m
α
α
.
3. Моменты или коэффициенты моментов, зависящие от угла откло-
нения рулей высоты обозначаются
в
вz
M
δ
δ
, или
в
вz
m
δ
δ
.
Моменты тангажа, обусловленные продольным вращ ательным
движением летательного аппарата
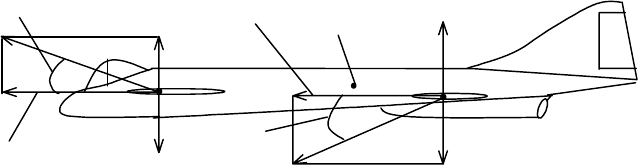
При вращении ЛА отно сительно центра тяжести с угловой скорос -
тью ω
z
(рис. 2) каждая точка его поверхности, кроме поступательной
скорости, приобретает дополнительную скорость, равную
z
rω
и направ-
Y
г.о
P
Y
р
Центр
тяжести
x
dкр
x
T
x
dг.о
Рис. 1. Силы, создающие моменты тангажа М
дв
и М
г.о
17
ленную перпендикулярно радиус-вектору r, соединяющему центр тяже-
сти с этой точк ой. В результате ме стные углы атаки элементов поверх-
ности отличаются от углов ат аки при поступ ательном движении. Изме-
нение углов приводит к появлению дополнительных аэродинамических
сил, которые можно свести к равнодействующей силе
()
z
R
∆ω
, прило-
женной в центре тяжести ЛА, и моменту
()
zz
M
∆ω
относительно попе-
речной оси, проходящей через центр тяжести. Величина
()
z
R
∆ω
очень
мала и в расчетах подъемной силы ЛА ею пренебрегают. Величина
же
()
zz
M
∆ω
существенно влияет на динамические свойства ЛА.
∆R
2
Центр
тяжести
V
∞
ω
z
r
–∆α
V
∞
∆R
1
+∆α
ω
z
r
Рис. 2. Силы, обусловленные продольным вращением ЛА
Как следует из рис. 2, момент, обусловленный угловой скоро стью
ω
z
, всегда направлен против вращения, по этому он называется демп-
фирующим моментом тангажа, или продольным демпфирующим мо-
ментом (способствует зату ханию колебаний, возникающих при откло-
нении ЛА от положения равновесия или при переходе от одного поло-
жения равновесия к другому). Опыт показывает, что величина демпфи-
рующего момента пропорциональна угловой скорости ω
z
() .
z
zz z z
MM
ω
∆ω= ω
Основными частями ЛА, создающими продольный демпфирующий
момент, являются горизонтальное оперение, крыло и фюзеляж ЛА. По-
этому можно записать
г.окр
ф
.
z
zzz
zzz
z
MMM M
ω
ωωω
=+ +
При неустановившемся движении ЛА коэффициенты аэродинами-
ческих сил и моментов зависят не только от значений α, δ, ω
z
, но и от
скорости угла атаки
α
"
и скорости перекладки руля
δ
"
. Пусть ЛА совер-

18
шает полет с некоторой скоростью V и с изменяющимся по времени
углом атаки. В соответ ствии с изменением угла атаки изменяется и скос
потока за крылом. Однако поток, отклоненный крылом, достигает го-
ризонтального оперения не мгновенно, а через некоторый промежуток
времени ∆t, зависящий от расстояния между передними и задними по-
верхно стями и от скорости потока в районе расположения горизонталь-
ного оперения V
1
(рис. 1)
г.окр
1
.
dd
xx
t
V
−
∆=
Следовательно, угол атаки горизонтального оперения в момент време-
ни t будет таким, который вызывается крыло м в момент времени t
1
= t – ∆t.
Изменение угла атаки крыла за время ∆t сост а вляет
г.окр
1
,
dd
xx
d
t
dt V
−
α
∆α = ∆ = α
"
а изменение угла скос а потока на горизонтальном оперении будет
.
α
∆ε = ε ∆α
Это запаздывание скос а потока приводит к появлению дополнитель-
ной силы на горизонтальном оперении
г.о
г.ог.ог.оу
Y С qS
α
∆= ∆ε
и, следовательно, дополнительного момента горизонтального оперения
относительно центра тяжести ЛА
г.о
г.от г.о
().
zd
MYxx∆=∆ −
Тогда коэффициент момента от запаздывания скоса потока можно
выразить
г.о
() .
z
z
A
M
m
qSb
−∆
α=
"
Знак минус перед выражением момента по ставлен потому, что по-
ложительное приращение подъемной силы горизонтального опере-
ния ∆Y
г.о
вызывает появление пикирующего (отрицательного) мо-

19
мента ∆M
z
. Соответствующая производная ко эффициента момента мо-
жет быть найдена
.
z
z
M
m
α
∂
=
∂α
"
"
Явление запаздывания скоса потока возникает не только при изме-
нении угла атаки, но и при изменении угла отклонения руля высоты,
если руль располагается на передней поверхности ЛА, т. е. это может
иметь место на ЛА, выполненном по схеме “утка”.
2.3. Продольная статическая устойчивость
летательного аппарата
Под статической устойчивостью движения понимается тенденция к
восстановлению исходного (равновесного) движения при его наруше-
нии возмущающим воздействием.
Обычно принято рассматривать это свойство относительно тех или
иных параметров движения. В продольном движении наибольший ин-
терес представляет статическая устойчивость по перегрузке (сохране-
ние постоянного угла атаки или перегрузки) и по скорости полета (со-
хранение постоянной скоро сти). Наличие тенденции вернуться к ис-
ходному равновесному значению параметра движения конечно еще не
означает безусловное его восстановление. Однако статическая устой-
чивость является необходимым, хотя и недо статочным условием дина-
мической устойчивости.
Устойчивость по перегрузке
Под исходным равновесным продольным движением ЛА понимают
такой его полет, при котором сумма моментов всех сил, действующих
на ЛА, равна нулю, т. е. m
z
0. Пусть ЛА, движущийся с постоянной ско-
ростью горизонтально (равновесное движение), вошел в вертикаль но
восх одящий по т ок воздуха, к о т орый движется со скоростью W
y
(рис. 3).
Очевидно, что в этом случае ЛА получит приращение угла атаки
y
∆α =
W
V
, а это приведет к нарушению равновесия сил и моментов,
появится неуравновешенная сила ∆Y(α) с точкой приложения в фокусе
ЛА. Аэродинамический фокус – это точка профиля крыла или ЛА, от-
носительно которой момент аэродинамических сил имеет постоянное
значение, не зависящее от угла атаки, т. е. точка, в которой
0
z
m
∂
=
∂α
.

20
V
∆Y
α
∆α
Центр
тяжести
F
W
y
Рис. 3. Приращение подъемной силы при восходящем потоке воздуха
В зависимости от взаимного расположения фокуса и центра тяжести
приращение угла атаки вызовет появление моментов: пикирующего (фо-
кус за центром тяжести), кабрирующего (фокус перед центром тяжес-
ти) и нулевого (фокус и центр тяжести совпадают).
Для того чтобы ЛА обладал тенденцией к восстановлению исходного
угла атаки (этот угол атаки называется балансировочным), необходимо
при положительном приращении ∆α возникновение отрицательного
продольного момента (момента пикирования) и наоборот.
Следовательно, тенденцией к восстановлению исходного угла атаки,
т. е. статической устойчивостью по углу атаки, обладает тот ЛА, у кото-
рого фокус располагается за центром тяжести. Указанное условие нали-
чия ст атической устойчивости по углу ат аки (критерий статической ус-
тойчивости) может быть записано в виде
б
б
0,
z
z
m
m
α
α=α
α=α
∂
=<
∂α
или
0
TF
xx
−<
.
Так как изменение угла атаки при постоянной скорости приводит к
изменению нормальной перегрузки на величину
()
y
Y
n
G
∆α
∆=
, пропор-
циональную углу ∆α, то ст атическая устойчивость по углу атаки равно-
ценна статической устойчивости по перегрузке.
В авиационной практике за меру статической устойчивости по пере-
грузке принята частная производная
y
C
z
m
от коэффициента момента m
z
и по коэффициенту подъемной силы С
у
, так как С
у
линейно зависит от
α в летном диапазоне углов атаки. Летательный аппарат тог да:
при
б
0
y
C
z
m
α=α
<
– устойчив по перегрузке;
