Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

2 Introduction to diffraction

If anomalous scattering takes place, the atomic scattering factor is

altered to take this into account. This occurs when the X-ray frequency

is close to the resonance frequency of an electron. Only some of the elec-

trons in the atom are affected and they will scatter the X-rays roughly

π/2 out of phase with the incident beam. Electrons scattering exactly

π/2 out of phase are represented mathematically by an imaginary com-

ponent of the scattering factor and they cease to contribute to the real

part. The exact phase change is very sensitive to the X-ray frequency.

This is shown in Fig. 1.2 that displays the real and imaginary parts of

the contribution to the atomic scattering factor of the anomalously scat-

tering electrons as a function of wavelength. The remaining electrons

in the atom are unaffected by this change in wavelength. Such informa-

tion on atomic scattering factors is obtained from quantum-mechanical

calculations.

–30

–20

–10

1.84 1.85

f

Δf

λ(Å)

Fig. 1.2 Real (f



) and imaginary (f ”) con-

tributions to anomalous scattering for the

example of a samarium atom.

1.4 X-ray scattering from a unit cell

X-rays scattered from each atom in the unit cell contribute to the overall

scattering pattern. Since each atom acts as a source of scattered X-rays,

the waves will add constructively or destructively in varying amounts

depending upon the direction of the diffracted beam and the atomic

positions. This gives a complicated diffraction pattern whose amplitude

and phase vary continuously, as can be seen in the two-dimensional

optical analogue in Fig. 1.3.

1.5 The effects of the crystal lattice

The diffraction pattern of the crystal lattice is also a lattice, known as

the reciprocal lattice. The name comes from the reciprocal relationship

between the two lattices – large crystal lattice spacings result in small

spacings in the reciprocal lattice and vice versa. The direct cell parame-

ters are normally represented by a, b, c, α, β, γ and the reciprocal lattice

parameters by a

∗

, b

∗

, c

∗

, α

∗

, β

∗

, γ

∗

. The direction of a

∗

is perpendicu-

lar to the directions of b and c and its magnitude is reciprocal to the

Fig. 1.3 Holes in an opaque sheet and their optical diffraction pattern.

1.6 X-ray scattering from the crystal 3

spacing of the lattice planes parallel to b and c; similarly for b

∗

and c

∗

A two-dimensional example of the relationship between the direct and

reciprocal lattices is shown in Fig. 1.4.

1.6 X-ray scattering from the crystal

A combination (convolution) of a single unit cell with the crystal lat-

tice gives the complete crystal. The X-ray diffraction pattern is therefore

given by the product of the scattering from the unit cell and the recip-

rocal lattice, i.e. it is the scattering pattern of a single unit cell observed

only at reciprocal lattice points. This can be seen in Fig. 1.5, which shows

the unit cell of Fig. 1.3 repeated on a lattice and its corresponding diffrac-

tion pattern. The underlying intensity is the same in both patterns. The

positions of the reciprocal lattice points are given by the crystal lattice;

the value of the diffraction pattern at a reciprocal lattice point is given

by the atomic arrangement within the unit cell.

Fig. 1.4 Direct lattice (left) and the corresponding reciprocal lattice (right).

Fig. 1.5 The unit cell of Fig. 1.3 repeated on a lattice and its diffraction pattern.

4 Introduction to diffraction

1.7 The structure-factor equation

There are many factors affecting the intensity of X-rays in the diffraction

pattern. The one that depends only upon the crystal structure is called

the structure factor. It can be expressed in terms of the contents of a

single unit cell as:

F(hkl) =



j=1

exp



2πi(hx

+ ky

+ lz

)



. (1.1)

The position of the jth atom is given by the fractional co-ordinates

, y

, z

), it has a scattering factor of f

and there are N atoms in the

cell. Structure factors are measured in number of electrons; they give a

mathematical description of the diffraction pattern such as that illus-

trated in Fig. 1.6. Each structure factor represents a diffracted beam

that has an amplitude, |F(hkl)|, and a relative phase φ(hkl). Mathemat-

ically, these are combined as |F(hkl)|exp[i φ(hkl)] and can be written as

F(hkl).

You may notice that the distribution of intensities in the diffrac-

tion pattern in Fig. 1.6 is centrosymmetric. This is an illustration of

Friedel’s Law that states that |F(hkl)|=|F(

hkl)|. The law follows from

(1.1) that shows that F(hkl) is the complex conjugate of F(

hkl), mak-

ing the magnitudes equal and relating the phases as ϕ(hkl) =−ϕ(hkl).

This is no longer true when the atomic scattering factor f

is also com-

plex. Changing the signs of the diffraction indices does not produce

the complex conjugate of f

, so Friedel’s Law is not obeyed when

there is anomalous scattering. However, the effect is phase dependent

and for centrosymmetric structures where all the phases are 0 or π ,

the magnitudes of F(hkl) and F(

hkl) are always changed by the same

amount.

Fig. 1.6 Part of the X-ray diffraction pattern of ammonium oxalate monohydrate.

1.8 The electron-density equation 5

The experimental measurements consist of the intensity of each beam

and its position in the diffraction pattern. After suitable correction fac-

tors are applied, the quantities recorded are h, k, l, |F(hkl)| or h, k, l,

|F(hkl)|

1.8 The electron-density equation

Animageof the crystal structurecan be calculated fromthe X-ray diffrac-

tion pattern. Since it is the electrons that scatter the X-rays, it is the

electrons that we see in the image, giving the value of the electron den-

sity at every point in a single unit cell of the crystal. The units of density

arethe number ofelectronsper cubicAngstrom unit – e/Å

. The electron

density is expressed in terms of the structure factors as:

ρ(xyz) =



hkl

F(hkl) exp



−2πi(hx + ky + lz)



, (1.2)

where the summation is over all the structure factors F(hkl) and V is

the volume of the unit cell. Note that the structure factors include the

phases φ(hkl) and not just the experimentally measured amplitudes

|F(hkl)|. Since the X-rays are diffracted from the whole crystal, the cal-

culation yields the contents of the unit cell averaged over the whole

crystal and not the contents of any individual cell. In addition, because

of the ﬁnite time it takes to perform the diffraction experiment, we see

a time-averaged picture of the electrons. This results in a smeared-

out image of each atom because of its thermal vibration, as seen in

Fig. 1.7.

Fig. 1.7 A section of the 3D electron density map of a planar molecule.

6 Introduction to diffraction

1.9 A mathematical relationship

Notice the mathematical similarity between (1.1) and (1.2). Equation

(1.1) transforms the electrondensity (inthe form of atomic scattering fac-

tors, f

) to thestructurefactors F(hkl), while (1.2) transforms the structure

factors back to the electron density. These are known as Fourier trans-

forms – one equation performing the inverse transform of the other. This

is a mathematical description of image formation by a lens. Light scat-

tered by an object (Fourier transform) is collected by a lens and focused

into an image (inverse transform). In the optical case, the (real) image

is inverted and this is seen mathematically by the appearance of the

negative sign in the exponent of (1.2).

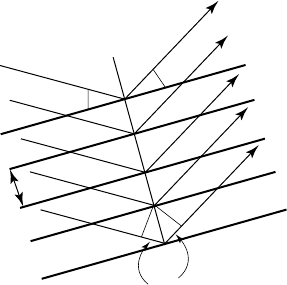
1.10 Bragg’s law

We cannot go far into X-ray diffraction without mentioning Bragg’s law.

This gives thegeometrical conditions underwhich a diffracted beam can

be observed. Figure 1.8 shows rays diffracted from lattice planes and,

to get constructive interference, the path difference should be a whole

number of wavelengths. This leads to Bragg’s law which is expressed as:

2d sin θ = nλ, (1.3)

where θ is known as the Bragg angle, λ is the wavelength of the X-rays

and d is the plane spacing. The ﬁgure suggests the rays are reﬂected from

the crystal planes. They are not – it is strictly diffraction – but reﬂection is

mathematically equivalent in this context and the name X-ray reﬂection

has stayed with us since Bragg ﬁrst used it. The value of n in Bragg’s

law can always be taken as unity, since any multiples of the wavelength

can be accounted for in the diffraction indices h, k, l of any particular

reﬂection. For example, n = 2 for the planes h, k, l is equivalent to n = 1

for the planes 2h,2k,2l.

Lattice planes hkl

hkl

2 x d

hkl

sin u

Fig. 1.8 Diffraction of X-rays from crystal lattice planes illustrating Bragg’s law.

1.11 Resolution 7

1.11 Resolution

In X-ray crystallography we have effectively a microscope that gives

images of crystal structures, although its realization is different from an

ordinary optical microscope. What is the resolution of the image and

what is its magniﬁcation? By convention, the resolution is given by the

minimum value of d that appears in Bragg’s law. This will correspond

to the maximum value of θ. With Mo Kα radiation and all data collected

to a maximum θ of 25

◦

, Bragg’s law gives:

sin(25

◦

)

0.71

min

1/2

(1) 5.5 Å

1/2

(2) 2.5 Å

1/2

(3) 1.5 Å

1/2

(4) 0.8 Å

1/2

Fig. 1.9 The electron density calculated from a diffraction pattern of limited extent,

indicated by the decreasing values of d

min

from (1) to (4).

8 Introduction to diffraction

producing a resolution (d

min

) of 0.84 Å. The maximum possible reso-

lution is λ/2, which occurs when sin(θ

max

) = 1. For Cu Kα radiation

this will be 0.77 Å, similar to the resolution obtained with Mo Kα for

max

= 25

◦

. Figure 1.9 shows the effect on the electron density of

imposing different limits on the extent of the diffraction pattern used to

produce it.

If an electron density map is displayed on a scale of 1 cm/Å, this

corresponds to a magniﬁcation of 10

. You should be impressed by this

very large number.

1.12 The phase problem

The measured X-ray intensities yield only the structure-factor ampli-

tudes and not their phases. The calculation of the electron density can

not therefore be performed directly from experimental measurements

and the phases must be obtained by other means. Hence, the so-called

phase problem. Methods of overcoming the phase problem include:

(i) Patterson search and interpretation techniques,

(ii) direct methods,

(iii) use of anomalous dispersion,

(iv) isomorphous replacement,

(v) molecular replacement.

Methods (i) and (ii) are the most important in small-molecule crystal-

lography; the others feature in macromolecular crystallography.

Introduction to symmetry

and diffraction

William Clegg

2.1 The relationship between a crystal

structure and its diffraction pattern

A crystal structure and its diffraction pattern are related to each other,

in both directions, by the mathematical procedure of Fourier transfor-

mation, the details of which are considered elsewhere. The diffraction

pattern is the Fourier transform of the crystal structure, corresponding

to the pattern of waves scattered from an incident X-ray beam by a single

crystal; it can be measured by experiment (only partially, because the

amplitudes are obtainable from the directly measured intensities via a

number of corrections, but the relative phases of the scattered waves are

lost), and it can be calculated (giving both amplitudes and phases) for a

known structure. In turn, the crystal structure is the Fourier transform of

the diffraction pattern and is expressed in terms of the electron-density

distribution concentrated in atoms; it can not be measured by direct

experiment, because the scattered X-rays can not be refracted by lenses

to form an image as is done with light in an optical microscope, and it

can not be obtained directly by calculation, because the required relative

phases of the waves are unknown.

Part of an X-ray diffraction pattern of a single crystal is shown, as

a computer-generated reproduction, in Fig. 2.1. It consists of a pattern

of discrete spots with a range of intensities (represented as different

sizes of spot). This pattern has a deﬁnite geometry, and a degree of

symmetry in the positions and intensities of the individual spots, in

this case a combination of horizontal and vertical reﬂection (with an

inversion point at the centre of the pattern), so that only one quarter of

the pattern is unique, the other three quarters being symmetry related

to it. The full diffraction pattern, of course, is three-dimensional; only

part of a section through it is shown here.

The geometry of the pattern can be described by measuring the

distances between spots and angles between rows of spots. In this exam-

ple, the pattern is rectangular, with perpendicular rows, and this is a

10 Introduction to symmetry and diffraction

Fig. 2.1 Part of an X-ray diffraction pattern.

necessary consequence of the reﬂection symmetry present; the horizon-

tal and vertical spacings are different.

Measurement of the geometry of a diffraction pattern gives informa-

tion about the regular arrangement of molecules in the crystal structure.

The symmetry of the pattern is related to the symmetry of the solid-state

arrangement of molecules. The intensities, among which there is no

obvious relationship except for the symmetry, hold information about

the actual shapes and orientations of molecules, i.e. the positions of

atoms in the crystal structure. The biggest task in determining a crys-

tal structure is measuring these (usually thousands of) intensities and

extracting the details of the atomic arrangement from them, but this can

not be done without an understanding of the geometry and symmetry

relationships as well. Here, we concentrate on symmetry aspects.

2.2 Translation symmetry in

crystalline solids

Chemists are most familiar with symmetry in its application to individ-

ual molecules, as expressed in their point groups, particularly through

aspects of group theory in bonding and spectroscopy. Symmetry plays a

very important part in crystallography, and its application to crystalline

solids includes concepts additional to those for isolated molecules.

A perfectly crystalline solid material consists of a very large (effec-

tively inﬁnite) number of identical molecules (or assemblies of a few

molecules) arranged in a precisely regular way repeated in all direc-

tions, to give a high degree of order (theoretically zero entropy). This

repetitionin a regular pattern of anindividual structural unit, in an iden-

tical form and orientation, is a form of symmetry, called translation, and

it is the most fundamental characteristic of the crystalline solid state.

2.2 Translation symmetry in crystalline solids 11

All perfect crystals display translation symmetry in three dimensions,

whether or not any other symmetry elements (rotation, reﬂection and

inversion)arealso present;they areoptional, but translation is necessary.

The two-dimensional manifestation of translation symmetry is familiar

in the form of patterns on clothing and other materials, wallpaper, etc.

A complete crystal structure can be speciﬁed by describing the con-

tents of one repeat unit, together with the way in which this unit is

repeated by translation symmetry. The translation symmetry is deﬁned

by the lattice of the structure and given numerical expression in the

parameters of a unit cell; here are two terms of vital importance in

crystallography.

In order to obtain the lattice of a particular crystal structure, choose

any single point in any repeat unit of the structure (for example, one

atom), and mark it with a dot. Find all the other points in the struc-

ture that are identical to this one (i.e. with identical surroundings, in

exactly the same orientation) and mark them also. Now keep the dots

and remove the structure. What remains is just a regular inﬁnite array

of points in three dimensions. This is the lattice; all the points are iden-

tical, equivalent to each other by translation symmetry. The operation

of translation is that of moving from one point to any equivalent one.

The lattice shows the repeating nature of the structure but not the actual

form (contents) of the structural repeat unit. Starting with a different

point and repeating the whole process would give exactly the same

result, and it is not necessary to choose the lattice points to lie on atoms

(in the majority of real crystal structures they do not, because there are

conventions that put them by preference on symmetry elements that lie

between molecules and relate them to each other; more on this later).

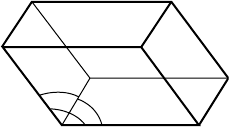
Fig. 2.2 A unit cell.

Any translation from one lattice point to another can be represented

as a vector, because it has a deﬁnite length and a certain direction. All

such vectors, for an arbitrary choice of any two lattice points, can be

constructed by putting together multiples of three basic unit vectors that

are the shortest three non-coplanar vectors between pairs of adjacent

lattice points:

t = ua + vb + wc,

where a, b, c are the unit vectors for this lattice, and u, v, w are integers

(positive, zero, and negative values are allowed). The complete lattice

geometry can thus be deﬁned by the three base vectors. In order to

do this with pure numbers rather than vectors, it is necessary to give

the lengths of the three vectors and the angles between each pair of

them (three angles altogether). By standard convention, the three vector

lengths are called a, b, and c, and the angles are called α, β, and γ ; α is

the angle between b and c, β is the angle between c and a, and γ is the

angle between a and b. These three vectors and 9 others equivalent to

them enclose a shape that is the three-dimensional equivalent of a two-

dimensional parallelogram (called a parallelepiped), similar to a brick

but not generally with 90

◦

angles. This shape is called the unit cell of

the crystal structure (and of its lattice); see Fig. 2.2. One unit cell is thus