Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

This page intentionally left blank

Fourier syntheses

William Clegg

8.1 Introduction

The crystal structure we are trying to determine and its X-ray diffraction

pattern are related to each other by the mathematical process of Fourier

transformation; each is the Fourier transform of the other, as shown in

the introductory material. It is worth beginning here with a summary

of the fundamental relationships involved and some comments on the

notation and its meaning.

X-rays are scattered by the electrons in a crystal structure, so what

we are able to determine is the electron-density distribution, averaged

over time and hence over the vibrations of the atoms. Since the crystal

structure is periodic, we need determine only the contents of one unit

cell, and the presence of symmetry other than pure translation reduces

this even further, to the asymmetric unit of the structure, which is a

fraction of the unit cell in all cases except space group P1.

The electron density is a smoothly varying continuous function with a

single numerical value (in units of electrons per cubic Ångstrom, e Å

−3

)

at each point in the structure. For many of the calculations involved

in crystallography this is not a convenient function to work with, and

we describe the structure instead in terms of the positions and dis-

placements (vibrations) of discrete atoms, each with its own electron

density distribution about its centre. In most studies (except for high-

resolution charge-density experiments), atoms are taken to be spherical

in shape when stationary, ignoring valence effects such as bonding and

lone pairs of electrons, and their individual contributions to X-ray scat-

tering, known as atomic scattering factors, are calculated from electron

densities derived from quantum mechanics. These atomic scattering fac-

tors are known mathematical functions, varying with Bragg angle θ,

available in published tables (such as the International Tables for Crys-

tallography), and incorporated in standard crystallography computer

programs. The X-ray scattering effects of atoms are modiﬁed by atomic

displacements, which cause the at-rest electron density to be spread

out over a larger volume and usually unequally in different directions

(anisotropic), and this effect is described by a set of anisotropic dis-

placement parameters (adps) for each atom. The most commonly used

mathematical model uses six adps and can be represented graphically

as an ellipsoid. This model is a reasonable approximation to physical

reality in most cases.

103

104 Fourier syntheses

Thus, each symmetry-independent atom in the asymmetric unit of

a crystal structure is described by the following parameters: a known

atomic scattering factor (f), a set of displacement parameters (U values),

and three co-ordinates (x, y, z) specifying its position. (In some cases,

such as disordered structures, another parameter is used, giving the

site occupancy factor, because a site may be occupied by an atom in

some unit cells and not in others, at random, so on average we have to

specify a fraction of an atom here.) We give atomic positions relative to

one corner of one unit cell chosen as the origin, and measuredalong each

of the unit cell axes. Rather than using Å as units for the co-ordinates,

we give them as fractions of the unit cell axis lengths, and these fractions

do not have units. This means, for example, that the origin of the unit

cell has co-ordinates 0,0,0 and the point right in the centre of the unit cell

has co-ordinates

2. It is convenient to take most co-ordinates to lie

in the range 0–1, but molecules do not generally lie conveniently within

the conﬁnes of an arbitrarily deﬁned unit cell, so some co-ordinates

may be negative or be greater than 1. A majority of co-ordinates outside

the range 0–1 simply means a poorly chosen unit cell origin, with the

molecule lying largely or entirely outside the ‘home’ unit cell. This is,

of course, not strictly incorrect, since all unit cells are exact copies of

each other by deﬁnition, and any integer can always be added to or

subtracted from all x, all y,orallz co-ordinates, but it is bad practice.

8.2 Forward and reverse Fourier transforms

The diffraction pattern (a set of discrete reﬂections, each a wave with

its own amplitude and relative phase) is the Fourier transform of the

crystal structure. The mathematical relationship for this is given by:

F(hkl) =



j=1

exp[2πi(hx

+ ky

+ lz

)]. (8.1)

Here, f

is the atomic scattering factor for the jth atom in the unit cell,

which has co-ordinates x

, y

, z

; f

incorporates the effects of atomic dis-

placements in this equation, in order to keep it simple. The integers h, k

and l are the indices for one particular reﬂection, occurring in a certain

direction, and this equation shows how the structure factor F for that

reﬂection is related to the crystal structure. What this equation means

in words is that each reﬂection in the diffraction pattern is a wave and

it is made up as a sum of waves scattered by the individual atoms, each

atom in accordance with its electron-density distribution (f

); in adding

up the waves scattered in this direction, their relative phases have to

be allowed for, and these depend on the positions of the atoms relative

to each other, as expressed in the exponential term. For mathematical

convenience and compactness, complex number notation is used (hence

the symbol i), allowing us to use just one symbol to represent both the

amplitude and phase together for a wave. F(hkl) is a complex number,

8.2 Forward and reverse Fourier transforms 105

as explained in Chapter 1 and Appendix A, with an amplitude and a

phase. Equation (8.1) applies once for each reﬂection (each direction in

which a discrete diffracted beam occurs) in order to obtain the complete

diffraction pattern, and each calculation involves the sum of N terms,

this being the number of atoms in the unit cell. The presence of sym-

metry in the structure allows the calculations to be simpliﬁed further,

because symmetry-equivalent reﬂections have the same amplitude and

related phases, but we shall keep with general equations here.

Equation (8.1) can be used to calculate the expected diffraction pattern

for any known structure, and it is used at various stages during a crystal-

structure determination, even when the ‘knownstructure’isincomplete.

We referto the resultof this as a set of calculated structure factors, F

(hkl)

or just F

Equation (8.1) also describes mathematically the physical process

observed when X-rays are diffracted by a crystal, which is the exper-

iment of collecting diffraction data. From the experiment, however, we

obtain only the amplitudes of the reﬂections (derived from the mea-

sured intensities) and not their phases. Thus, we have a set of observed

structure factors, but they are only |F

|. We do not have any observed

phases, so the observed diffraction pattern is, in this sense, incomplete.

One particular F is never measured in the diffraction experiment, but

is important for future use. This is the structure factor F(000), corre-

sponding to completely in-phase scattering by all atoms in the forward

direction with θ = 0, and it can not be physically separated from the

undiffracted beam. Setting all indices to zero in (8.1) and noting that

atomic displacement parameters have no effect at zero Bragg angle, we

ﬁnd that F(000) has an amplitude equal to the total number of electrons

in one unit cell, and has a phase of zero.

That is half the story, which we may call the forward Fourier trans-

form. The other half is the reverse Fourier transform. The crystal

structure, expressed as electron density, is the Fourier transform of the

diffraction pattern. This relationship is expressed as:

ρ(xyz) =



hkl

F(hkl) exp[−2π i(hx + ky + lz)]. (8.2)

There is an obvious similarity to (8.1), with the terms for the diffraction

patternandfor the crystal structureexchanged between the leftandright

sides of the equation. The main differences otherwise are the inclusion

of the unit cell volume V in (8.2) (to make sure the units are correct,

since the crystal structure here is described by its electron density ρ

instead of by discrete atomic scattering factors that, like structure factor

amplitudes, have units of electrons rather than e Å

−3

), and the presence

of a minus sign in the exponential.

Equation (8.2) is the basis of all Fourier synthesis calculations in crys-

tallography. It shows how the electron density in the crystal structure

can, in principle, be obtained from the diffraction pattern. Like the

forward Fourier transform, it describes a physical process, but this time

106 Fourier syntheses

one that is unachievable in an experiment. It is the equivalent of the use

of lenses in an optical microscope to take light scattered by an object

being viewed, and recombine the scattered waves to produce a focused

image of the object; unfortunately X-rays can not be bent by lenses in

the same way as visible light, or we would be able to build an X-ray

supermicroscope and not have so much work to do! The equation says

that, in order to ﬁnd the electron density at a particular point in the

structure, we have to take all the individual scattered X-ray waves (the

reﬂections F) and add them together, allowing for their different relative

phases. The phase differences will vary with the position at which we

are ﬁnding the electron density, because the waves will have different

path lengths in converging on that point, and this is the meaning of the

exponential term again; but the waves also have different phases from

their initial production in the diffraction process (given by the forward

Fourier transform), and these have to be included as well.

Since this physical process can not actually be carried out, we have

to emulate it by calculation, using (8.2). Unfortunately, this is still not

possible in a direct way, because we do not have all the information

required. In (8.2), F(hkl) are complex numbers, with an amplitude and

a phase: although we have the structure factor amplitudes, we do not

know the intrinsic relative phases of the reﬂections. Much of the task of

solving a crystal structure is recovering the lost phase information, at

least as approximate values, so that the reverse Fourier transform can

be carried out.

Modiﬁed versions of (8.2) are used at various stages in a crystal-

structure determination, as our knowledge of the phases develops from

non-existenttoessentially complete, and these arereferredtoas different

kinds of Fourier syntheses or Fourier maps.

In order for (8.2) to give an accurate result for the electron density,

it is not only necessary to have phases and to have accurate values for

the reﬂection amplitudes (i.e. good data!); we should, in principle, also

include all possible reﬂections with indices between −∞ and +∞. This

is clearly unachievable, and the effect is to produce some distortions in

the electron density, which may be seen as small ripples surrounding

the atoms, most noticeable around atoms with high electron density.

It is, however, not usually a signiﬁcant problem, since the form of

atomic scattering factors, together with atomic displacements, means

that diffraction intensities decrease at higher Bragg angles, and the

unmeasured high-index small amplitudes would not contribute much

to the Fourier summations anyway. Inclusion of F(000) is important

in order to obtain correct electron density values, since all other terms

effectively contribute no net electron density to the total in the unit cell,

because they are waves consisting of equal positive and negative parts.

A Fourier synthesis may be thought of as smearing out the correct total

number of electrons uniformly throughout the unit cell (this is the F(000)

term) and then redistributing this density by successive addition of

other waves, each of which will reduce the density in some regions and

increase it in others by the same amount; the ﬁnal result has the electron

8.3 Some mathematical and computing considerations 107

density concentrated in discrete maxima corresponding to atoms, with

low or zero (but never negative) electron-density regions in between.

8.3 Some mathematical and computing

considerations

Since Fourier transform calculations, both forward and reverse, take up

a very high proportion of the amount of computing involved in crystal-

lography, they need to be carried out as efﬁciently as possible. The scale

of the task can be illustrated easily. For the forward Fourier transfor-

mation, consider a unit cell of dimensions 10×10×10 Å

containing 60

atoms. Typically, this will give about 7000 reﬂections up to a maximum

θ of 25

◦

with Mo-Kα radiation. Calculation of the diffraction pattern F

thus involves 7000 sums (ignoring symmetry), in each of which there

are 60 terms. This makes 420 000 calculations, each of which includes

exponentials, multiplications and additions. This is a relatively small

structure!

For the reverse Fourier transformation, consider the same crystal

structure. From (8.2) we obtain values of the electron density at discrete

points in the unit cell, not a continuous function. This means calculat-

ing values at selected points on a three-dimensional grid covering the

unit cell. In order to resolve adjacent atoms and make good use of the

available data, a grid spacing of about 0.3 Å is reasonable, giving about

37 000 grid points. So, (8.2) has to be used 37 000 times, each one being

a sum of 7000 terms, making a total of about 260 million calculations.

And this is for just one Fourier synthesis.

The presence of symmetry does reduce the size of the task, of course,

because symmetry-equivalent reﬂections have the same amplitude and

related (not generally equal) phases, so the forward Fourier trans-

formation only has to be carried out for the symmetry-unique data

set. Similarly, the electron density need be calculated only for the

asymmetric unit, and not for the complete unit cell.

In addition, there are various well-known mathematical procedures

for simplifying the calculations involved, because of the properties of

sines and cosines of sums of terms, as shown in Appendix A. The

details of these do not need to concern us here; although Fourier

calculations were carried out by hand in the early pioneering days

of crystallography before the widespread availability of fast comput-

ers (and were often restricted to one- and two-dimensional synthe-

ses rather than full three-dimensional studies, to provide projections

of electron density, from which full structures were subsequently

deduced), these calculations are now performed at very high speed in

‘black boxes’.

It should be noted that the phases of reﬂections can take any value

between 0 and 360

◦

(0 and 2π radians) for non-centrosymmetric struc-

tures. By contrast, phases are restricted to a choice of two values,

0 and 180

◦

(0 and π radians) when a structure is centrosymmetric. This

108 Fourier syntheses

considerably simpliﬁes the mathematics, since the complex exponen-

tial terms collapse to real cosines, with disappearance of the imaginary

sine components. In pictorial physical terms, this means that each of the

waves being added together in (8.2) can only be completely in phase (0,

crest-to-crest) or completely out of phase (180

◦

, crest-to-trough), and

the problem of ﬁnding the unknown phases reduces to the smaller

(but still considerable) task of ﬁnding the unknown signs, positive or

negative, for the reﬂection amplitudes |F| in order to add the waves

together.

Fig. 8.1 Contoured section through a

Fourier synthesis in a plane containing B,

C, O and H atoms. The edge of a Pt atom

bonded to B is seen at the left. H atoms are

not visible; the ten clear peaks correspond

to atoms.

Fig. 8.2 Contoured section through a

Fourier synthesis in the plane containing

three methyl carbon atoms of a two-fold

disordered tert-butyl group. The major

component atoms are clearly seen as the

largest peaks, but the minor components

do not all give separate maxima. The small

peak at the centre is the outer edge of the

central carbon atom of the group, which

lies below this plane, where the electron

density is higher and reaches its maximum

for this atom.

A Fourier synthesis is a three-dimensional function, usually obtained

as a set of values on a three-dimensional grid. In chemical crystallog-

raphy, it is rare for such a result to be presented in full. Normally, the

positions of maxima (also called peaks) in the synthesis are found by

interpolation between the grid points (effectively a form of curve ﬁtting

in three dimensions) as part of the computing procedure, and these posi-

tions, together with the corresponding values of the electron density, are

listed and made available as potential atom sites for visual inspection

or, more likely, interpretation through a molecular graphics program.

In most cases, this works satisfactorily, but it causes problems when

atom sites are not clearly resolved from each other, giving no discrete

maximum in the synthesis. This is the norm in protein crystallogra-

phy, where data often do not extend to atomic resolution, and different

techniques are used. With atomic-resolution data, the most common

occurrence of this problem is in cases of disorder, when the alternative

sites may be too close together to give separate maxima. Inspection of

the full Fourier synthesis in the region of the disorder may be necessary.

This can involve taking planar sections through the three-dimensional

synthesis. Sections parallel to the unit cell faces are straightforward,

as these will correspond to the grid points on which the synthesis has

been performed, but sections in arbitrary orientations can also be calcu-

lated, either explicitly at appropriate points or by interpolation between

the points of the standard grid. The sections can be contoured with lines

joiningpointsofequalelectron density, like the contours showing moun-

tains on geographical maps, and this helps to show regions of electron

density that can correspond to atom sites, even if disorder is a problem.

Examples are shown in Fig. 8.1 and Fig. 8.2.

8.4 Uses of different kinds of

Fourier syntheses

All Fourier syntheses are essentially variations on (8.2). This may be

written in a slightly different but equivalent way to help show what the

variations are.

ρ(xyz) =



hkl

F(hkl)

exp[iφ(hkl)]exp[−2π i(hx + ky + lz)]. (8.3)

8.4 Uses of different kinds of Fourier syntheses 109

Here, the structure factor F has been separated into its amplitude |F|

and its phase φ, both of which are needed in order to carry out the

calculation.

Different kinds of Fourier syntheses use different coefﬁcients instead

of the amplitudes |F|, and they may also in some cases apply weights

to the individual terms in the sum, so that not all reﬂections contribute

strictlyin proportionto these coefﬁcients.These areall attemptstoobtain

asmuch useful information as possible at differentstages of the structure

determination, even if the phases are not well known.

8.4.1 Patterson syntheses

These are discussed in detail in the next chapter. The coefﬁcients are

instead of |F

|, and all phases are set equal to zero. In this case

all necessary information is known and the synthesis can be readily

performed. The result, of course, is not the electron density distribution

for the structure, but it is related to it in what is often a useful way, as

is explained later. There are some slight variations even within this use,

and these are covered in the Patterson synthesis chapter (Chapter 9).

8.4.2 E-maps

These are an important part of direct methods for solving crystal struc-

tures, and are discussed more fully in Chapter 10. The coefﬁcients are

|, the so-called normalized observed structure factor amplitudes,

which represent the diffraction pattern expected for point atoms (with

their electron density concentrated into a single point instead of spread

out over a ﬁnite volume) of equal size, at rest. E-values are calculated,

with a number of assumptions and approximations, from the observed

amplitudes |F

|, and only the largest values are used, weaker reﬂections

being ignored because they contribute less to the Fourier synthesis any-

way. Phases for this selected subset of the full data are estimated by

a range of techniques under the general heading of ‘direct methods’,

and usually a number of different phase sets are produced and used to

calculated E-maps. These maps tend to contain sharper (stronger and

narrower) maxima than normal Fourier syntheses (F-maps), and this

can help to show up possible atoms, but they also tend to contain more

noise (peaks, usually of smaller size, that do not correspond to genuine

atoms).

8.4.3 Full electron-density maps,

using (8.2) or (8.3) as they stand

These actually tend not to be used very often in chemical crystallog-

raphy, except for demonstration purposes, because the other types of

syntheses have particular advantages at different stages. However, let

us consider how we can carry out such a synthesis without having any

110 Fourier syntheses

experimental phases. Such a procedure can be used when some of the

atoms have been located (perhaps from direct methods or a Patterson

synthesis) and others still remain to be found. Once we have some

atoms, we can use them as a model structure, which we know is not

complete, but it contains all the information we currently have. From

the model structure we can use (8.1) to calculate what its diffraction

pattern would be. This will not be identical to the observed diffraction

pattern, but it should show some resemblance to it, the more nearly so

as we include more atoms in the correct positions. There are various

measures of agreement between the sets of observed and calculated

amplitudes, |F

| and |F

|, but the important thing is that the calcu-

lated diffraction pattern includes phases, φ

as well as amplitudes |F

Although these are not the same as the true phases we would really like

to know, they are currently the nearest thing we have to them. A Fourier

synthesis using coefﬁcients |F

| with the phases φ

would just repro-

duce the same model structure and get us nowhere, but combining the

true observed amplitudes |F

|with the ‘current-best-estimate’ phases φ

gives us a new electron-density map. If the calculated phases are not too

far from the correct phases (as is usually the case if the model structure

has atoms in approximately correct places and these are a signiﬁcant

proportion of the electron density of the structure), then this usually

shows the atoms of the model structure again, together with new fea-

tures not in the model structure but demanded by the diffraction data,

i.e. more genuine atoms. Because of all the approximations involved in

this process, there may also be peaks in the electron-density map that

do not correspond to real atoms, and the results need to be interpreted

in the light of chemical structural sense and what is expected. Addi-

tion of these new genuine atoms gives a better model structure, and

the whole process can be repeated, giving better calculated phases and

yet another new, and clearer, Fourier synthesis. This is done repeatedly

until all the atoms have been found and the model structure essentially

reproduces itself.

8.4.4 Difference syntheses

These are widely used in preference to full electron-density syntheses

for expanding partial structures. The coefﬁcients are |F

|−|F

| and the

phases are obtained from a model structure as described above. The

result is effectively an electron-density map from which the features

already in the model structure are removed, so that new features stand

out more clearly, and it usually makes it easier to ﬁnd new atoms. This

is rather like saying that, if the tallest peaks in a range of mountains

were somehow taken away, the foothills would appear to be much more

impressive! Peaks lying at the positions of atoms in the model structure,

or negative difference electron density there, indicate that the model

has either too little or too much electron density in those places, and can

indicatea wronglyassigned atom type, e.g.Ninstead of O orNinstead of

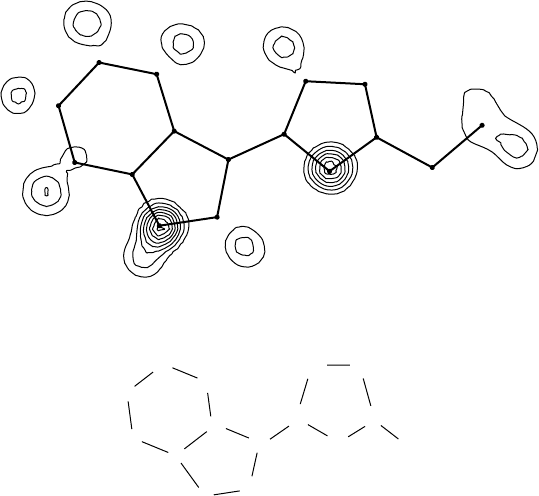
8.4 Uses of different kinds of Fourier syntheses 111

Fig. 8.3 A section through a difference synthesis showing the effect of wrongly assigned

atom types and missing hydrogen atoms; the assumed model structure is shown, together

with the positions of its atoms and bonds in the map.

C for these respective effects. An example is shown in Fig. 8.3. There are

potentially some considerable problems with difference syntheses when

the proportion of known atoms is quite small, because the calculated

phases can have large errors.Also, weak reﬂections with relatively large

uncertainties in their intensities can cause disproportionate errors, and

it may be best not to use the weakest reﬂections; alternatively they can

be given reduced weights, as discussed below. It is important to ensure

that the observed and calculated data are on the same scale. Another

reason why difference syntheses can be better than full F

syntheses is

that series termination errors (small ripple effects due to the lack of data

beyond the measured θ

max

) cancel out through use of the differences

instead of full amplitudes.

8.4.5 2F

− F

syntheses

The use of coefﬁcients 2|F

|−|F

| with phases calculated from a model

structure combines theadvantages of standard F

and difference synthe-

ses. The resulting map shows both the known and the as-yet unknown

features of the structures, with the new atoms emphasized, and it is

less subject to some of the errors of the simple difference synthesis.

It is more widely used in protein crystallography than by chemical

crystallographers.