Blake A.J.(ed.) Crystal Structure Analysis

Подождите немного. Документ загружается.

112 Fourier syntheses

8.4.6 Other uses of difference syntheses

Towards the end of structure determination, difference maps are often

used to locate hydrogen atoms. These can not usually be found until

all other atoms are present and have been reﬁned with anisotropic

displacement parameters, so that their contributions are correctly rep-

resented in the model structure. This is because hydrogen atoms have

very little electron density, and even that is signiﬁcantly involved in

bonding, so the positions found in difference maps are usually closer to

the nearest atom than are the actual centres (the nuclei) of the hydrogen

atoms. Unless data are of good quality, and particularly when heavy

atoms are present in the structure, hydrogen atoms can easily be lost in

the noise of an electron-density map. This is particularly true for non-

centrosymmetric structures, where the absence of hydrogen atoms in a

model structure is partially compensated by shifts in the phases from

their correct values; any Fourier synthesis using calculated phases will

always have a bias towards the model structure from which they were

obtained. Hydrogen atoms contribute relatively more to low-angle and

less to high-angle reﬂections, because their atomic scattering factor falls

off more quickly with θ than those of other atoms, so it may help to

leave out the high-angle data, or use weights that reduce their contri-

bution to the sums. Right at the end of a structure determination, when

reﬁnement is complete, a ﬁnal difference synthesis must be generated

in order to see if there is any remaining electron density unexplained

by the reﬁned model. This must include all data and use no weights.

Residual electron density may be an artefact of inadequate data correc-

tions (usually absorption), or may indicate poorly modelled disorder or

other problems and imperfections in the model. The sizes of the largest

maxima and minima in this ﬁnal difference map, together with their

positions if they are of signiﬁcant size, are important indicators of the

quality of a structure determination, and should always be included in

any summary of the results.

8.5 Weights in Fourier syntheses

It was noted above that the calculated phases, derived from the current

model structure, are only an estimate of the true phases. Clearly the

approximation improves as the model structure becomes more com-

plete. In any given set of calculated phases, some will be more in error

than others. For a reﬂection with large and almost equal |F

| and |F

there is greater conﬁdence in the reliability of the phase than there is

when |F

| is small. This variation in reliability of the phases can be

incorporated into the calculations by multiplying each contribution by

a weight, which increases with expected reliability. Various weight-

ing schemes have been developed and used, with weights calculated

from the values of the observed and calculated amplitudes and the pro-

portion of unknown electron density in the structure. Appropriately

8.6 Illustration in one dimension 113

chosen weights can help to enhance the genuine new features of

Fourier syntheses and reduce noise. Weights that are θ-dependent can

be used to aid the search for hydrogen atoms in the later stages, by

down-weighting the higher-angle datacontaining less information from

these atoms. No weights may be used in the ﬁnal difference synthe-

sis for checking the completeness of a reﬁned structure; by this stage

the calculated phases will be as close to the correct values as they

can be.

8.6 Illustration in one dimension

For a one-dimensional structure (this direction taken as the z-axis) with

inversion symmetry, (8.3) simpliﬁes considerably:

ρ(z) =



F(l)

s(l) cos[2π(lz)] (8.4)

and the Fourier summation can easily be demonstrated pictorially. Only

positive values of the index l need to be considered, each giving a double

contribution to the sum, since F(l) = F(−l), in addition to the single con-

tribution of F(0). The phase of each reﬂection is now just the (unknown)

positive or negative sign, s(l ) =+1or−1. We use some data measured

a number of years ago for a compound containing a long alkyl chain

and a bromine atom (the detailed molecular structure is not important

here); this crystallizes in a unit cell with one long axis (c), the molecule

being stretched out so that its projection along this axis gives resolved

atoms, Br and several C. There are two molecules per unit cell, appear-

ing as inversions of each other along the two halves of the cell axis. This

projection can be investigated with just the (00l) reﬂections, with the

irrelevant zero indices ignored here.

Table 8.1. One-dimensional Fourier

contributions.

l |F

||F

| true sign model sign

3817 +−

46451 −−

55664 −−

67455 −−

71526 −−

859 ++

94639 ++

10 45 53 ++

11 43 47 ++

12 17 26 ++

13 9 3 −−

14 26 28 −−

15 31 41 −−

16 23 39 −−

17 12 23 −−

18 14 1 +−

19 20 19 ++

20 33 31 ++

21 63 30 ++

0 z 1

Fig. 8.4 The contributions of each of

the reﬂections in Table 8.1 to the one-

dimensional Fourier synthesis, all shown

here with positive sign (zero phase angle);

the reﬂections are in order, with l = 3atthe

top and l = 21 at the bottom.

Table 8.1 lists the observed amplitudes of the measured reﬂections

with l between 3 and 21 (|F

|), and the amplitudes calculated from

a model structure consisting only of the two symmetry-equivalent Br

atoms (|F

|, via the one-dimensional equivalent of (8.1)); how these Br

atoms can be found from the data is considered in the next chapter, on

Patterson syntheses. Also given are two sets of signs (reﬂection phases):

the correct signs obtained by calculation from the complete structure

once it is known (true signs), and the signs obtained from the model

containing only the Br atoms (model signs). Below Table 8.1 are shown

in Fig. 8.4 the individual terms |F

(l)|cos[2π(lz)] that contribute to the

sum in (8.4), ignoring the signs s(l). Carrying out a Fourier synthesis

to obtain the one-dimensional electron density just means adding up

these ‘electron-wave’ contributions with the correct signs. Since there

are 19 terms to add together, the number of possible sign combina-

tions is 2

, which is over half a million: not a good case for trial

and error! Several different variants on (8.4) are shown graphically in

Figs. 8.5 to 8.8.

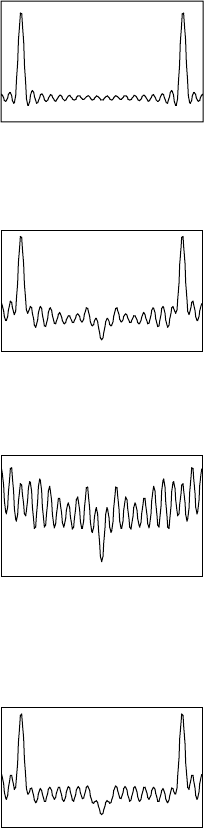
114 Fourier syntheses

8.6.1 F

synthesis

Both the amplitudes and the signs are taken from the model structure

(Br atoms only). This essentially just gives back the same model struc-

ture, with two large peaks where the Br atoms were located (Fig. 8.5).

However, there is signiﬁcant regular ripple in the restof the unit cell; this

is caused by ‘series termination’, the lack of contributions from reﬂec-

tions with l > 21. If these were available and were included, most of the

diagram would be essentially ﬂat. This is not a useful Fourier synthesis!

Fig. 8.5 F

synthesis: amplitudes from Br

atom, phases from Br atom.

Fig. 8.6 F

synthesis: observed ampli-

tudes, phases from Br atom.

8.6.2 F

synthesis, as used in developing

a partial structure solution

Experimental amplitudes |F

| are combined with the signs (phases)

obtained from the current model structure. The resulting map (Fig. 8.6)

shows the atoms of the model (2 Br), together with new atoms (a num-

ber of smaller peaks corresponding to C atoms in a chain for each

molecule). Note that the model signs are mostly, but not all, correct, so

this electron-density map is not perfect, but it is sufﬁcient to locate the

remaining atoms. The incorrect signs slightly distort the map, produc-

ing rather unequal peak heights for the carbon atoms and overstating

the central dip.

Fig. 8.7 F

− F

synthesis: difference

between observed and Br-calculated

amplitudes, phases from Br atom.

8.6.3 F

−F

synthesis

This is a difference map (Fig. 8.7), using the difference between the

observed and calculated amplitudes together with the signs from the

model structure. Comparison with the previous result shows that the Br

atoms in the model no longer appear, so the new atoms stand out more

clearly.

Fig. 8.8 F

synthesis: observed ampli-

tudes, ‘correct’ phases from ﬁnal structure.

8.6.4 Full F

synthesis

This is the same as the second result, but with all the correct phases.

This gives a more even pattern of peaks for the carbon atoms (Fig. 8.8).

At this stage, with the structure complete, the model structure should

essentially reproduce itself in a standard |F

|synthesis, and a difference

synthesis should contain no signiﬁcant features.

Exercises 115

Exercises

1. In Fig. 8.3, assign the correct atom types, the H atoms,

and the appropriate bond types (single, double, or

aromatic). The correct formula is C

O. Why

is there only one peak visible for the ethyl group

H atoms?

2. What would be the effect on a Fourier synthesis of:

a) omitting the term F(000);

b) omitting the 20% of reﬂections with highest values

of (sin θ)/λ;

c) omitting the 5% of reﬂections with lowest values

of (sin θ)/λ;

d) setting all phases equal to zero?

This page intentionally left blank

Patterson syntheses for

structure determination

William Clegg

9.1 Introduction

We wish to convert a measured diffraction pattern into the corre-

sponding crystal structure that produced it experimentally. The process

involved is Fourier transformation, and the mathematical expression for

this was given in the previous chapter, on Fourier syntheses.

ρ(xyz) =



hkl

F(hkl)

exp[iφ(hkl)]exp[−2πi(hx + ky + lz)] (9.1)

This is the form of the equation that explicitly contains the amplitudes

and phases of the structure factors as separate symbols, from which

we can see the fundamental problem we face: the amplitudes |F

| are

known from the diffraction experiment, but the phases φ are unknown,

so it is not possible to carry out the Fourier synthesis directly. In the

previous chapter we saw that knowledge of part of the structure can

get us started, since it is then possible to calculate approximate phases

and improve our knowledge of the electron density in stages through

modiﬁed versions of (9.1). The question is, how do we make a start? In

chemical crystallography there are two main techniques for solving the

phase problem, which have complementary strengths and applications.

One is the use of so-called direct methods, which attempt to estimate

approximatephases fromrelationshipsamong the structurefactors with

no prior knowledge about the crystal structure itself (except for the dis-

crete atomic nature of matter and its implications for diffraction effects),

and this is considered in the next chapter. The other is the use of the

Patterson synthesis (or Patterson map, or Patterson function), another

variation on (9.1), which can provide information on approximate posi-

tions of some of the atoms in the structure. The Patterson synthesis

ﬁnds most use either when there are a few heavy atoms (atoms with

a considerably higher number of electrons) among many light atoms,

such as in co-ordination complexes of most metals, or when a signiﬁcant

proportion of the molecular structure is expected to have a well-deﬁned

117

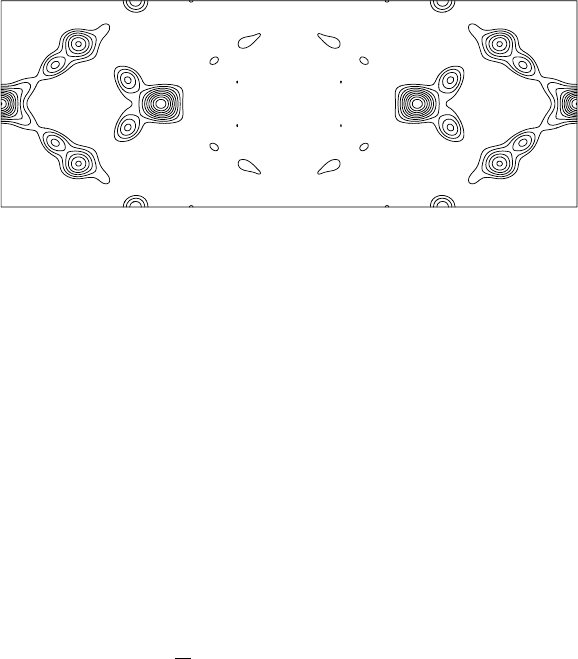
118 Patterson syntheses for structure determination

Fig. 9.1 A section through a Patterson map for an organic compound containing no heavy

atoms.

and known rigid internal geometry, such as the characteristic tetracyclic

framework of steroids or other fused polycyclic systems with little or

no conformational ﬂexibility.

In the Patterson synthesis (named after its inventor, A. L. Patterson),

the amplitudes |F

| in (9.1) are replaced by their squares |F

and the

unknown phases are simply omitted (effectively all set at zero). An

alternative way of expressing this is that the complex structure factors

F(hkl), which contain both amplitude and phase information (see (8.2)

in Chapter 8) are replaced by the product of each one with its complex

conjugate F

∗

(hkl). Multiplying any complex number by its complex con-

jugate (which has the same cosine term but the opposite sign for its sine

term) gives a real number, the imaginary terms cancelling out. In this

case the complex exponential also simpliﬁes to a real cosine.

P(uvw) =



hkl

F(hkl)

cos[2π(hu + kv + lw)]. (9.2)

Obviously, with these changes in the Fourier coefﬁcients and omission

of the phases, the result of the synthesis will no longer be the desired

electron density, but it turns out to be closely related to it in what can be

a useful way. The use of the co-ordinates u, v, w instead of x, y, z helps to

emphasize this point; these are still fractions of the unit cell edges and

the Patterson synthesis is a periodic continuous function looking rather

similar to an electron-density distribution and repeated in each unit cell.

Figure 9.1 is an example.

9.2 What the Patterson synthesis means

The nature of the Patterson synthesis and its relationship to the electron

density can be expressed in a number of ways that look rather different

but are essentially equivalent. The peaks in a Patterson map do not

correspond to the positions of individual atoms (i.e. the positions of

atoms relative to the unit cell origin as expressed in their co-ordinates

x, y, z), but instead to vectors between pairs of atoms in the structure

(i.e. the positions of atoms relative to each other). Thus, for every pair

9.2 What the Patterson synthesis means 119

of atoms in the structure with co-ordinates (x

, y

, z

) and (x

, y

, z

)

there will be a peak in the Patterson map (a maximum in the Patterson

synthesis) at the position (x

− x

, y

− y

, z

− z

) and also one at the

position (x

− x

, y

− y

, z

− z

), each atom giving a vector to the

other. To turn this argument the other way round, every peak observed

in the Patterson map corresponds to a vector between two atoms in the

crystal structure, so a Patterson peak at (u, v, w) means there must be

two atoms whose x co-ordinates differ by u, y co-ordinates differ by v,

and z co-ordinates differ by w. The objective is to work out some atom

co-ordinates by knowing only differences between pairs of them.

Mathematically this can all be expressed in terms of Fourier trans-

forms and convolutions. Multiplying two functions together in direct

space corresponds to a convolution of their Fourier transforms in recip-

rocal space, and vice versa. Calculating the Patterson synthesis involves

taking the product of the diffraction pattern structure factors with their

complex conjugates, so the result is the convolution of the electron den-

sity with its inverse. What this convolution means can be visualized

by adding together n versions of the true electron density, where n is

the number of atoms in the unit cell; for each contribution to the sum,

the whole structure is shifted to put this atom at the origin of the unit

cell and the electron density everywhere is multiplied by the electron

density of the atom at the origin.

P(u, v, w) =



cell

ρ(x, y, z)ρ(u − x, v − y, w − z)dxdydz, (9.3)

and this is the mathematical equation corresponding to the description

above in terms of vectors between pairs of atoms, because the value of

the Patterson function P will only be large at positions that correspond

to separations between signiﬁcant concentrations of electron density

according to (9.3).

The practical value of this synthesis can be seen by considering some

of the properties that follow from its deﬁnition.

1. There is a vector between every pair of atoms in the structure;

this includes ‘self-vectors’ between each atom and itself, which

obviously have zero length. For n atoms in the unit cell this means

vectors, of which n all coincide at the position (0, 0, 0), the origin

of the unit cell in the Patterson map. All Patterson maps have their

largest peak at the origin. There are n

−n other peaks, many more

than the number of atoms.

2. Every pair of atoms gives two vectors, A→B and A←B. These

are equal and opposite, so there are two peaks related to each

other by inversion through the origin.All Patterson syntheses have

inversion symmetry, whether or not the crystal structure has. This

consequence can also be seen from the form of (9.2): setting all

phases equal to zero automatically forces an inversion centre. Per-

haps less obvious, but equally true, is that screw axes and glide

120 Patterson syntheses for structure determination

planes in the crystal structure are converted into normal rotation

axes and mirror planes in the Patterson synthesis, all translation

components disappearing. This means the point group symme-

try for a Patterson synthesis is the same as the Laue class for the

diffraction pattern. The primitive or centred nature of the unit cell

of the structure is retained in the Patterson synthesis, so the space

group symmetry of the Patterson map is related to the true space

group of the structure, but there are only 24 possible Patterson

space groups, corresponding to the combinations of the 11 Laue

classes with appropriate permissible unit cell centrings in each of

the crystal systems.

3. Patterson peaks have a similar appearance to electron-density

peaks, but they are about twice as broad as a result of the convo-

lution effect of (9.3). Because of this and the large number of peaks

resulting from the ﬁrst point above, there is a considerable overlap

of peaks, so they are usually not all resolved from each other like

electron-density peaks. Vectors that are approximately or exactly

equal in length and parallel to each other, such as opposite sides

of benzene rings and metal–ligand bonds arranged trans to each

other, will give substantial or complete overlap, further reducing

the number of distinct maxima that can be seen. Symmetry in the

structure also leads to exact overlap of vectors. Thus, Patterson

maps often show large relatively featureless regions.

4. Each peak resulting from a vector between two atoms has a size

proportional to the product of the atomic numbers Z of those two

atoms, just as electron-density peaks are proportional to atomic

numbers in normal Fourier syntheses (ignoring the effects of

atomic displacements, which spread out the electron density some-

what). If the unit cell contains a relatively small number of heavy

atoms among a majority of lighter ones, the peaks correspondingto

vectors between pairs of these heavy atoms will be large and will

stand out clearly from the general unresolved background level

and smaller peaks.

Before going on to consider the two major ways of exploiting these

properties of the Patterson function, we note some small modiﬁcations

to the standard Patterson synthesis expression in (9.2) that can be used,

just as there are variations in Fourier syntheses that incorporate phase

information.

The ﬁrst is that it is possible to remove the large origin peak, so that

peaks corresponding to short vectors are more clearly seen, though this

is not usually a problem. In any case, the fact that the origin peak has

a size proportional to the sum of Z

for all atoms in the unit cell, on

the same scale as the sizes of other peaks described above, can help to

conﬁrm the identity of the atoms contributing to individual peaks. To

removethe origin peak,|F|

in (9.2) is replaced by |F|

−|F|



, wherethe

term subtracted is the mean value of |F|

at this Bragg angle, obtained by

some kind of curve ﬁtting to a plot of |F|

against (sin θ )/λ, for example.

9.3 Finding heavy atoms from a Patterson map 121

The second modiﬁcation is to sharpen the Patterson function, reduc-

ing the width of the peaks. This is achieved by using |E|

instead of

|F|

in (9.3), giving greater relative weight to the higher-angle data

and effectively suppressing the effects of atomic displacements. The

advantage is a better resolution of peaks from each other, but the disad-

vantage is introduction of more noise (spurious small peaks) because of

greater uncertainty in the higher-angle data and the enhanced effects of

series termination. Use of |E|

− 1 as coefﬁcients in the synthesis gives

both sharpening and origin-peak removal simultaneously. Intermediate

degrees of sharpening as a compromise are obtained by using |E||F| or

even

√

(|E|

|F|) as coefﬁcients.

9.3 Finding heavy atoms from

a Patterson map

If a unit cell contains a small number of heavy atoms together with

a majority of lighter atoms, then the Patterson map will show a rel-

atively small number of large peaks corresponding to heavy–heavy

vectors, prominent above the smaller peaks due to heavy–light vec-

tors and (probably largely unresolved) light–light vectors. The idea is

to deduce a set of heavy-atom positions that explain all the large Patter-

son peaks; these heavy atoms then form a model structure from which

approximate phases can be calculated for Fourier syntheses to develop

the model further, as already described in the previous chapter. There

are generally more vectors providing information than there are atom

positions to be found. Solving a Patterson map is rather like a math-

ematical brain-teaser or a crossword puzzle. Heavy atoms that are in

symmetry-related positions often give Patterson peaks lying in special

positions with co-ordinates equal to 0 or

2, which are easily recognized.

This is best illustrated with speciﬁc examples in commonly occurring

space groups.

9.3.1 One heavy atom in the asymmetric unit of P1

In this common case, there are two heavy atoms in the unit cell, related

to each other by inversion symmetry. Their unknown co-ordinates are

(x, y, z) and (−x, −y, −z). The largest Patterson peak is, as always, at

(0, 0, 0). There should be two other prominent peaks, one on each side

of the origin, since the Patterson function is also centrosymmetric. One

has co-ordinates (u, v, w) = (2x,2y,2z), because this is the difference

between the sets of co-ordinates of the two heavy atoms; the other has

the same co-ordinates with opposite signs, (−2x, −2y, −2z). It is a triv-

ial matter to divide these by 2 and obtain the position of the unique

heavy atom. Because there are two Patterson peaks, there are two pos-

sible answers, differing only in the signs of the co-ordinates; they are

equally correct, corresponding to different choices of the asymmetric

unit within the unit cell.