Biringen S., Chow C.-Y. An Introduction to Computational Fluid Mechanics by Example

Подождите немного. Документ загружается.

52 INVISCID FLUID FLOWS

Furthermore, if the ﬂuid is assumed incompressible, the velocity ﬁeld must

also satisfy the continuity equation for such a ﬂuid:

∇ · V = 0 (2.1.3)

Upon substitution from (2.1.2), (2.1.3) becomes

∇

φ = 0 (2.1.4)

where ∇

≡ ∇ · ∇ is the Laplacian operator, and (2.1.4) is called the Laplace

equation.

Using Prandtl’s postulation, the problem of an incompressible ﬂow past a given

streamlined body at high Reynolds numbers is to be solved as follows. For the

external region a velocity potential is to be found by solving the Laplace equation

(2.1.4), which satisﬁes both the boundary condition prescribed far upstream and

the requirement that the ﬂuid velocity be tangent to the body surface. The latter

condition is justiﬁed by the fact that the boundary layer around the body is thin.

The velocity distribution of the external ﬂow along the body surface is then used

as the outer boundary condition for the boundary-layer ﬂow. This inner ﬂow

satisﬁes the no-slip condition at the rigid wall and is a solution to the governing

boundary-layer equations to be shown in the next chapter.

In the present chapter the boundary-layer ﬂow is disregarded completely. Once

the velocity ﬁeld in the external region is determined from the kinematic con-

siderations just described, the pressure ﬁeld p can be computed from a dynamic

relation, called the Euler equation:

=−∇p (2.1.5)

It is the equation of motion for inviscid ﬂuids with body forces omitted. In this

equation ρ is the density, and the operator

≡

∂

∂t

+V ·∇ (2.1.6)

is the total or substantial derivative that gives the rate of change by following a

ﬂuid particle.

It is easier to compute the pressure from the integrated form of the Euler

equation (i.e., the Bernoulli equation) than from the Euler equation itself. Under

the conditions of incompressible ﬂuid and irrotational velocity ﬁeld, the Bernoulli

equation has the form

∂φ

∂t

+p +

ρV

= H (2.1.7)

where the constant of integration, H ,istheBernoulli constant. For a steady ﬂow,

(2.1.7) simply states that the sum of the hydrostatic pressure, p, and the dynamic

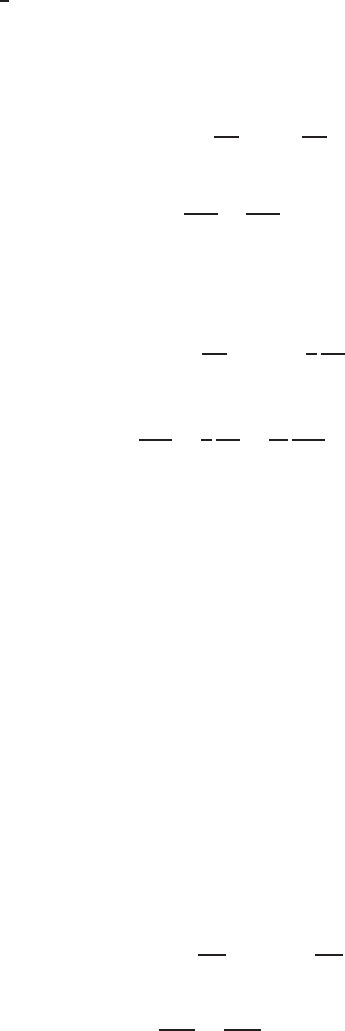
INCOMPRESSIBLE POTENTIAL FLOWS 53

pressure,

ρV

, is a constant at any point in the ﬂow. In this case H is the

stagnation pressure, or the pressure measured at a point where the ﬂuid velocity

vanishes.

For two-dimensional planar ﬂows, (2.1.2) and (2.1.4) can be expressed in

Cartesian coordinates as

u =

∂φ

∂x

, υ =

∂φ

∂y

(2.1.8)

and

∂

∂x

∂

∂y

= 0 (2.1.9)

where u and υ are, respectively, the velocity components along the x and y axes.

In polar coordinates, however, they have the expressions

∂φ

∂r

, u

∂φ

∂θ

(2.1.10)

and

∂

∂r

∂φ

∂r

∂

∂θ

= 0 (2.1.11)

where u

is the velocity component in the radial direction and u

is the velocity

component in the azimuthal direction.

Instead of velocity potential, stream function is sometimes used for analyzing

planar or axisymmetric incompressible ﬂows. The continuity equation (2.1.3)

suggests that the velocity vector can also be derived from a vector potential

through the relationship

V = ∇ × (i

ψ) (2.1.12)

where i

is a unit vector along the z axis, which is perpendicular to the plane of

ﬂuid motion, and ψ is called the stream function, which represents the volume

of ﬂuid passing per unit time between a given point and a reference streamline

(see, for example, Kuethe and Chow, 1998, Section 2.6). Streamlines,towhich

the instantaneous velocity vectors are tangent, are described by the equations

ψ = constant. In terms of stream function, the irrotationality relation (2.1.1)

becomes

∇ × ∇ ×(i

ψ) = 0 (2.1.13)

(2.1.12) and (2.1.13), when written in Cartesian coordinates, have the expressions

u =

∂ψ

∂y

, υ =−

∂ψ

∂x

(2.1.14)

∂

∂x

∂

∂y

= 0 (2.1.15)

54 INVISCID FLUID FLOWS

or, in polar coordinates, the expressions

∂ψ

∂θ

, u

=−

∂ψ

∂r

(2.1.16)

∂

∂r

∂ψ

∂r

∂

∂θ

= 0 (2.1.17)

It turns out that, similar to the velocity potential, the stream function for planar

incompressible ﬂows is also governed by the Laplace equation. However, the

nonsteady term in the Bernoulli equation cannot be written in terms of ψ in a

simple form similar to that shown in (2.1.7) in terms of φ.

The continuity equation (2.1.3) does not apply in regions where ﬂuid mass is

created or destroyed. The formulation is now generalized to include the possi-

ble sources and sinks in the ﬂow ﬁeld. Consider an inﬁnitesimal control volume

x y z ﬁxed in the Cartesian coordinate system as sketched in Fig. 2.1.1, in

which the z dimension is not shown for the purpose of simplicity. The distribu-

tion of sources is represented by q(x, y, z, t), which is the volume of ﬂuid created

per unit time from a unit volume located at the point (x, y, z ). A simple arith-

metic procedure computing the volume ﬂuxes across the surfaces, as indicated

in Fig. 2.1.1 (the ﬂuxes in the z direction can easily be added), shows that the

net volume of ﬂuid ﬂowing out of the control volume per unit time is



∂u

∂x

∂υ

∂y

∂w

∂z



x y z

FIGURE 2.1.1 Flow through a control volume.

NUMERICAL SOLUTION OF SECOND-ORDER ORDINARY DIFFERENTIAL EQUATIONS 55

For an incompressible ﬂuid, this amount of ﬂuid must be equal to qx y z,

or the amount produced by all the sources contained within the volume. Thus,

the resulting continuity equation is

∂u

∂x

∂υ

∂y

∂w

∂z

= q(x, y, z , t) (2.1.18)

or, in vector notation,

∇ · V = q (2.1.19)

Sinks are represented by negative values of q. In the absence of sources or sinks,

q = 0, and the continuity equation (2.1.3) is recovered.

When the velocity vector is expressed in terms of velocity potential, (2.1.19)

becomes

∇

φ = q (2.1.20)

whichisintheformofaPoisson equation.

Despite the fact that both Laplace and Poisson equations are linear, analytical

solution for ﬂow past a body of arbitrary shape is by no means simple. Vari-

ous numerical and seminumerical solution techniques will be introduced in the

following sections.

An extensive discussion on potential ﬂows is out of the scope of this book.

Such a task can be found in any introductory book on ﬂuid dynamics.

2.2 NUMERICAL SOLUTION OF SECOND-ORDER ORDINARY

DIFFERENTIAL EQUATIONS: BOUNDARY-VALUE PROBLEMS

In connection with the numerical solution of ordinary differential equations, var-

ious initial-value problems were treated in Chapter 1. In another class of ﬂuid

dynamic problems a solution is to be found that satisﬁes not only the differen-

tial equation throughout some domain of its independent variable, but also some

conditions on boundaries of that domain. These problems are called boundary-

value problems. We consider here the numerical solution of a linear second-order

ordinary differential equation of the form

+A(x)

+B(x)f = D(x) (2.2.1)

for the domain x

min

≤ x ≤ x

max

, subject to the boundary conditions that the values

of f are given at the end points of that range, at x = x

min

and x

max

. The method

developed here will be modiﬁed later for solving problems involving derivative

boundary conditions.

As the ﬁrst step in our numerical method, the differential equation is to be

approximated by an equation of the ﬁnite-difference form. Similar to what was

done in solving the initial-value problems, the axis of the independent variable

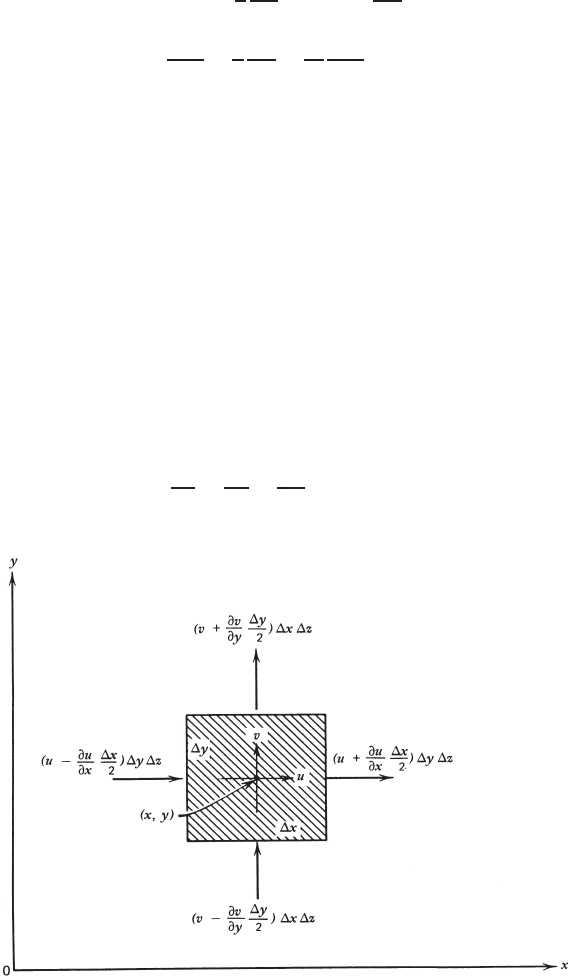
is again subdivided into small intervals of constant width h. If the number of

intervals in the given range of x is n +1, and if the end points of the intervals

56 INVISCID FLUID FLOWS

are labeled according to the index notation shown in Fig. 2.2.1, starting with x

at the left end of the range, then the following relations hold:

= x

+ih, i = 0, 1, 2, ..., n +1 (2.2.2)

in which x

= x

min

and x

n+1

= x

max

. Values of the function f evaluated at these

end points are also named in index notation according to the deﬁnition f

≡ f (x

It is desired to approximate the derivatives of f at an arbitrary point x

expressions containing values of f evaluated in the neighborhood of x

Let x

be such a neighboring point with j = i +m,wherem is a positive

or negative integer. For small values of h the function evaluated at x

may be

expanded in a Taylor’s series about x

≡ f (x

+mh)

= f

+mhf



(mh)



(mh)



+··· (2.2.3)

where a prime denotes a differentiation with respect to x. By assigning the values

−1and+1tom in (2.2.3), we obtain two expressions for f (x) at immediate

neighboring points of x

i−1

= f

−hf





−



+··· (2.2.4)

i+1

= f

+hf







+··· (2.2.5)

FIGURE 2.2.1 Numerical solution of an ordinary boundary-value problem.

NUMERICAL SOLUTION OF SECOND-ORDER ORDINARY DIFFERENTIAL EQUATIONS 57

There are many different ways of computing a particular derivative. For

example, f



may be solved for from (2.2.5) to give



i+1

−f

) −



−



−···

With a truncation error O(hf



), it is approximated by



i+1

−f

) (2.2.6)

This a forward-difference formula for the ﬁrst-order derivative, so named because

it involves the values of the function at x

and at a point ahead of it. On the other

hand, if we use (2.2.4), a backward-difference formula of the form



−f

i−1

) (2.2.7)

is obtained whose truncation error is of the same order of magnitude as the one

associated with the previous formula, except for a difference in sign. Thus, the

approximations (2.2.6) and (2.2.7) will give similar accuracies in a numerical

computation. A more accurate approximation, having an error of O(h



),is

obtained by subtracting (2.2.4) from (2.2.5); this has the form



i+1

−f

i−1

) (2.2.8)

Because of its appearance on the right-hand side, it is called a central-difference

formula for f



. Formulas giving any desired accuracies can be obtained by

assigning additional values to m in (2.2.3) and using the same technique just

demonstrated.

To approximate the second-order derivative of f , we show only a central-

difference formula



i+1

−2f

i−1

) (2.2.9)

having an error O(h

). It is obtained by adding (2.2.4) and (2.2.5) to eliminate



. Formulas of various truncation errors for computing derivatives up to the

fourth order are tabulated by McCormick and Salvadori (1964, Section 3.2).

We now return to the differential equation (2.2.1). To allow errors of the same

order of magnitude in the two derivatives shown in that equation, we use the

central-difference formulas (2.2.8) and (2.2.9). Thus, at a point x

, the differential

equation (2.2.1) is approximated by the difference equation

i+1

−2f

i−1

) +

i+1

−f

i−1

) + B

= D

58 INVISCID FLUID FLOWS

where A

, B

,andD

denote, respectively, A(x

), B(x

),andD(x

). Multiplying

the equation by h

and grouping similar terms, we obtain



1 −



i−1

+(−2 +h



1 +



i+1

= h

It can be written in a more convenient form

i−1

i+1

= C

(2.2.10)

by calling

= 1 −

=−2 +h

= 1 +

= h

(2.2.11)

The preceding coefﬁcients are known constants at any interior point in the spec-

iﬁed range of x. Equation (2.2.10), applied at i = 1, 2, ..., n, gives the set of n

linear algebraic equations to be solved simultaneously for the n unknowns f

Special attention is needed when i = 1andn are assigned in (2.2.10). These

two equations are

= C

and

n−1

n+1

= C

Since f

and f

n+1

are known from boundary conditions, the two involved terms

on the left side are constant and therefore are moved to the right. To simplify the

appearance of our program, we assign the value of (C

−C

) to C

and the

value of (C

−C

n+1

) to C

. This action may be expressed symbolically as

← (C

−C

)

← (C

−C

n+1

)

(2.2.12)

After this rearrangement, C

and C

disappear from the left side and the set of

n simultaneous equations becomes, when expressed in matrix notation,

⎡

⎢

⎣

00··· 000

0 ··· 000

0 C

··· 000

········ · ·

0000··· C

n−1,1

n−1,2

n−1,3

0000··· 0 C

⎤

⎥

⎦

⎛

⎜

⎝

n−1

⎞

⎟

⎠

⎛

⎜

⎝

n−1,4

⎞

⎟

⎠

(2.2.13)

NUMERICAL SOLUTION OF SECOND-ORDER ORDINARY DIFFERENTIAL EQUATIONS 59

The coefﬁcient matrix on the left-hand side of (2.2.13) is called a tridiagonal

matrix, whose nonvanishing elements form a band, three elements wide along

the diagonal. This particular set of equations can be solved by using the Gaussian

elimination method. According to this method, we multiply the second equation

in (2.2.13) by C

and the ﬁrst by C

and then take the difference of the two to

eliminate f

. The resulting equation is

−C

) f

= C

−C

In this equation, if we call the coefﬁcient of f

by the name C

,thatoff

by the

name C

, and the group on the right-hand side by the name C

, and if the ﬁnal

equation is used to replace the second equation in (2.2.13), the form of (2.2.13)

will remain unchanged except that C

is replaced by zero. Working with the new

second equation and the third equation in (2.2.13), C

can be eliminated by using

the same technique. The same process is repeated until C

n−1,1

is eliminated. In

summary, the eliminating processes are achieved by successively renaming the

coefﬁcients according to the following assignments:

← (C

i−1,2

−C

i−1,3

)

← C

i−1,2

← (C

i−1,2

−C

i−1,4

)

⎫

⎬

⎭

i = 2, 3, ..., n − 1 (2.2.14)

At this stage, all the equations in (2.2.13) are in the simple form of having

only two terms on the left-hand side. The value of f

can immediately be found

by solving simultaneously the last two equations in (2.2.13). Thus,

n−1,2

−C

n−1,4

n−1,2

−C

n−1,3

(2.2.15)

It can easily be veriﬁed that the remaining unknowns can be calculated, in a

backward order, from the recurrence formula

−C

j+1

, j = n −1, n −2, ...,2,1 (2.2.16)

The numerical method just described is now summarized as follows. The dif-

ferential equation (2.2.1) is ﬁrst replaced by a set of difference equations (2.2.10),

whose coefﬁcients are calculated according to (2.2.11). Boundary conditions are

taken care of by executing the actions shown in (2.2.12). Finally, the unknowns

, with i = 1, 2, ..., n, are computed by following the procedure represented by

(2.2.14) to (2.2.16). The last part of the computation will be programmed under

a subroutine named

TRID, which will appear in the next program.

Later in Chapter 4, we introduce other efﬁcient methods for solving tridiag-

onal equations, i.e., the compact-storage Thomas algorithm based on Gaussian

elimination, and the LU decomposition, which is especially useful when many

systems have to be solved with the same coefﬁcient matrix but with different

right-hand-sides, such as in parabolic partial differential equations with constant

coefﬁcients.

60 INVISCID FLUID FLOWS

2.3 RADIAL FLOW CAUSED BY DISTRIBUTED SOURCES

AND SINKS

The numerical method just described for solving boundary-value problems is

applied in this section to solve a ﬂow problem with a known solution, so that

the accuracy of the method can be tested. The method will be used later in

Section 3.3 on problems whose solutions cannot be obtained analytically.

Consider a radial ﬂow in the domain r

≤ r ≤ 4r

, within which there is an

axisymmetric distribution of sources whose strength increases linearly with r.

For such a problem the governing equation (2.1.20) becomes





φ = q

(2.3.1)

where q

is the source strength at r = r

. The radial velocity is computed from

(2.1.10):

dφ

(2.3.2)

It is always more convenient to work with dimensionless equations. If u

represents a characteristic velocity, the following dimensionless variables can be

introduced.

R =

,  =

, U =

(2.3.3)

It follows that in the domain 1 ≤ R ≤ 4, the ﬂow is described by the dimension-

less equations





 = αR (2.3.4)

and

U =

d

(2.3.5)

in which α = q

is a dimensionless source strength. Equation (2.3.4) has a

general solution of the form

 =

αR

+β ln R + γ

The ﬁrst term on the right-hand side is the particular solution representing the

ﬂow caused by the source distribution. The homogeneous solution consists of

two terms: the ﬁrst represents a line source located at R = 0 having strength β,

and the second is just a constant. Since the velocity ﬁeld is not affected by the

constant term in , γ may conveniently be set to zero. Thus, for α = 9and

β =−24, the expression

 = R

−24 ln R (2.3.6)

INVERSE METHOD I: SUPERPOSITION OF ELEMENTARY FLOWS 61

is the exact solution of the equation



d

= 9R (2.3.7)

satisfying the boundary conditions

 = 1atR = 1

 = 64 −24 ln 4 at R = 4

(2.3.8)

The corresponding dimensionless radial velocity is, from (2.3.5),

U = 3R

−

(2.3.9)

To solve numerically the boundary-value problem consisting of the differential

equation (2.3.7) and boundary conditions (2.3.8), the equation is ﬁrst compared

with the standard form (2.2.1) to obtain

A(R) =

B(R) = 0

D(R) = 9R

(2.3.10)

The independent variable in these relations has already been changed from the

original x to R. The details of the numerical computation are depicted in Program

2.1, in which the range of R between 1 and 4 is divided equally into 30 intervals.

Once the values of  evaluated at the interior points are obtained following

the procedure described in the previous section, the radial velocity, which is the

ﬁrst-order derivative of  according to (2.3.5), is computed using the central-

difference formula



i+1

−

i−1

(2.3.11)

The numerical results for  and U are then printed out to compare with the

exact solutions represented by (2.3.6) and (2.3.9).

The output of Program 2.1 (Table 2.A.1, see Appendix) shows that the errors

of the numerical solution are less than 1% in φ and 0.2% in U ,whichmaybe

considered satisfactory in most engineering problems. Results of higher accura-

cies can be obtained by increasing the number of intervals at the cost of longer

computing time. You may verify this statement by comparing the data obtained

by varying the number of intervals in Program 2.1.

2.4 INVERSE METHOD I: SUPERPOSITION OF ELEMENTARY FLOWS

In the previous numerical example, we look directly for a solution to the

governing equation that satisﬁes a set of assumed boundary conditions. Such

boundary-value problems are common in studying potential ﬂows. For example,

in the problem of a uniform ﬂow past a body of given shape, a solution to the