Biringen S., Chow C.-Y. An Introduction to Computational Fluid Mechanics by Example

Подождите немного. Документ загружается.

42 FLOW TOPICS GOVERNED BY ORDINARY DIFFERENTIAL EQUATIONS

0 0.2 0.4 0.6 0.8 1

−0.2

−0.1

0.1

0 0.2 0.4 0.6 0.8 1

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2 0.4 0.6 0.8 1

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

(e) T = 0.1

(f) T = 0.15

(g) T = 0.2

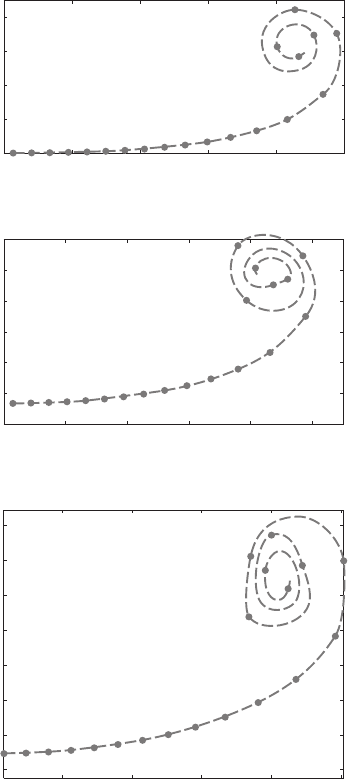
FIGURE 1.7.5 (continued)

region. Results at later time steps show that the paths of some vortices in that

region are contorted, and certain parts of the vortex sheet may become crossed.

The computation should actually be terminated before this unrealistic situation has

developed. The chaotic motion of the spiral has been found by several authors.

A brief description of some previous research works is referred to in Moore

(1974). To eliminate the chaotic motion, Moore successfully used a concentrated

tip vortex to represent the tightly rolled portion of the vortex sheet.

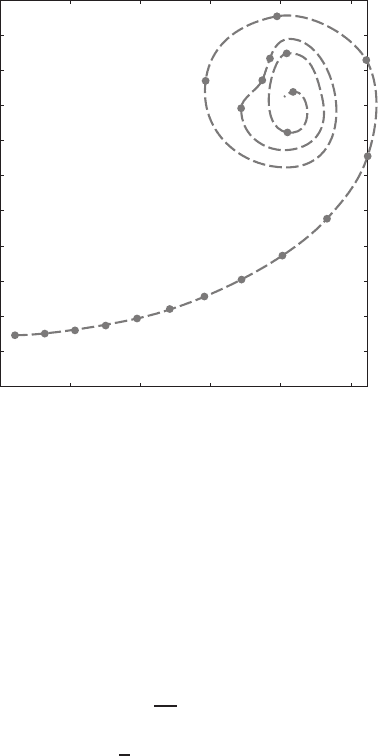
ROLLING UP OF THE TRAILING VORTEX SHEET BEHIND A FINITE WING 43

0 0.2 0.4 0.6 0.8 1

−0.9

−0.8

−0.7

−0.6

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

(h) T = 0.35

FIGURE 1.7.5 (continued)

Results of higher accuracies can be obtained by choosing larger values for m.

However, the computing time increases roughly with m

. Let us now apply our

result to a realistic problem. For a Boeing 747 with half-span a = 30 m and a total

weight of 4 ×10

N, the circulation averaged along the span is 815 m

/s during

take off at sea level at a speed of 67 m/s. Assuming an elliptical distribution of

circulation along the span, as described by (1.7.4),

2a ·(815) =



−a



−x

)

1/2

πa

giving 

= 1038 m

/s. The characteristic time 2πa





is about 5.45 s, and

therefore the last plot for T = 0.35 in Fig. 1.7.5 shows the vortex sheet con-

ﬁguration at t = 1.91 s. For a take-off speed of 67 m/s, this is the approximate

conﬁguration of the three-dimensional trailing vortex sheet at a distance of 128 m

behind the airplane. The plot also shows that after the sheet has been rolled up,

the centers of the two spirals are separated by a distance shorter than the wing

span b.

Figure 1.7.5 also reveals that the tip region of the vortex sheet descends

slower than the middle region. The vertical position of the midpoint of the sheet

descends initially with speed 



2a, and slows down toward a constant speed

approximately equal to half of that value.

44 FLOW TOPICS GOVERNED BY ORDINARY DIFFERENTIAL EQUATIONS

The analysis on which Program 1.7 was based may be improved. In that

analysis we subdivide a vortex sheet into small spanwise intervals and replace

each one by a point vortex at the center. Since the sheet strength γ is not

uniform, the vortices within each subdivision will generally induce a velocity

at its center. Thus, the discrete vortex placed there will move under its own

inﬂuence. This motion was not taken into account, although its magnitude may

be small compared with the sum of those induced there by other point vortices.

To be more realistic, when a vortex sheet segment is replaced by a discrete

vortex, it should be placed at a point on that segment at which the self-induced

velocity is zero. The computation for determining the position of such a point

for a straight segment can be carried out without any difﬁculty. However, after

the segment is deformed into a curve, the location of the point of vanishing self-

induced velocity changes. The determination of its position on an arbitrary curve

becomes too involved to be considered practical.

Instead of being replaced by initially equispaced vortices, as demonstrated

here, the vortex sheet may also be replaced by discrete vortices of equal strength.

Moore’s results based on these two approximations show remarkable agreement.

Project for Further Study: Replace the vortex sheet considered in Program

1.7 by 40 discrete vortices of equal strength. Plot the initial conﬁguration of the

sheet, and compare the shapes of the sheet with those shown in Fig. 1.7.5 at the

same time instants.

APPENDIX

List of Principal Variables in Program 1.1

Program Symbol Deﬁnition

(Main program)

A 1 +ρ



B (1 −ρ)g

C 3ρ



D Diameter of sphere, d,m

D1V, D2V, etc. Velocity increments, 

, 

,etc.

DIZ, D2Z, etc. Displacement increments, 

, 

,etc.

G Gravitational acceleration, g,m/s

H Time increment, h,s

NU Kinematic viscosity of ﬂuid, ν,m

PI π

RE Reynolds number vd



RHO Density of body, ρ, kg/m

RHOBAR Density ratio, ρ,orρ



(continues)

ROLLING UP OF THE TRAILING VORTEX SHEET BEHIND A FINITE WING 45

List of Principal Variables in Program 1.1 (continued)

Program Symbol Deﬁnition

RHOF Density of ﬂuid, ρ

, kg/m

T, T0 Time, t

, and initial time, t

, respectively, s

TMAX Maximum time of integration, s

V, V0 Velocity, v

, and initial velocity, v

, respectively, of the sphere, m/s

VV Velocity of sphere in vacuum, v

,m/s

Z, Z0 Position, z, and initial position, z

, respectively, of the sphere, m

ZV Position of sphere in vacuum, z

(Function F)

CD Drag coefﬁcient, c

F (B −CW|W|c

)



R Dummy name for Reynolds number

W Dummy name for velocity

List of Principal Variables in Program 1.2 Motion of a Simple Pendulum

Program Symbol Deﬁnition

(Main program)

A 1 +ρ



B (1 −ρ)g

C 3ρ



D Diameter of sphere, d,m

DT Time increment, s

G Gravitational acceleration, g,m/s

L Distance between the pivot axis and the center of sphere, l,m

NU Kinematic viscosity of ﬂuid, ν,m

PI π

RHO Density of spherical body, ρ, kg/m

RHOBAR Density ratio, ρ,orρ



RHOF Density of ﬂuid, ρ

, kg/m

T, T0 Time, t

, and initial time, t

, respectively, s

THETA, THETA0 Angular displacement of pendulum, θ, and its initial value, θ

respectively, degrees

THETAV Angular displacement in vacuum, θ

, degrees

TMAX Maximum time of integration, s

V, V0 Tangential velocity, v, and its initial value, v

, respectively, m/s

VV Tangential velocity in vacuum, v

,m/s

(continues)

46 FLOW TOPICS GOVERNED BY ORDINARY DIFFERENTIAL EQUATIONS

List of Principal Variables in Program 1.2 Motion of a Simple Pendulum (continued)

Program Symbol Deﬁnition

Y, Y0 Circumferential displacement, y or lθ, and its initial value, y

respectively, m

YV Circumferential displacement in vacuum, y

(Subprogram RUNGE)

D1P, D2P, etc. Increments 

, 

, etc. in (1.1.13)

D1X, D2X, etc. Increments 

, 

, etc. in (1.1.13)

(Function CD)

RE Reynolds number, Re

List of Principal Variables in Program 1.3 Vertical Motion of an Airfoil

Program Symbol Deﬁnition

(Main Program)

ALPHA, ALPHAD Angle of attack, α, in radians and that in degrees, respectively

ALPHA0 Angle of attack of a stationary wing, α

,rad.

BETA β, the dimensionless parameter ρ



DT Dimensionless time increment

DU Increment in dimensionless horizontal velocity

PI π

T, T0 Dimensionless time, T, and its initial value, respectively

TMAX Maximum time of integration, dimensionless

U Dimensionless horizontal wind velocity, U

V, V0 Dimensionless vertical velocity of wing, V , and its initial

value, respectively

Z, Z0 Dimensionless displacement of the wing, Z , and its initial

value, respectively

(Function CL)

CL Lift coefﬁcient of the wing, c

ROLLING UP OF THE TRAILING VORTEX SHEET BEHIND A FINITE WING 47

List of Principal Variables in Program 1.4 Motion of a Spherical Projectile

Program Symbol Deﬁnition

(Main program)

A 1 +ρ



B (1 −ρ)g

C 3ρ



D Diameter of sphere, d,m

DT Size of time steps, s

G Gravitational acceleration, g,m/s

H Size of increment in T

I Step counter

IFRPRT Frequency of printing

J Counter for different cases

NU Kinematic viscosity of ﬂuid, ν,m

PI π

RHO Density of body, ρ, kg/m

RHOBAR Density ratio, ρ,orρ



RHOF Density of ﬂuid, ρ

, kg/m

T, T0 Time, t

, and initial time, t

, respectively, s

THETA0 Elevation of the projectile, θ

,deg

U Horizontal component of body velocity, u,m/s

V Vertical component of body velocity, v,m/s

W0 Initial speed of body, w

,m/s

X, X0 Horizontal position of body, x, and its initial

value x

, respectively, m

Y, Y0 Vertical position of body, y, and its initial

value, y

, respectively, m

(Functions FX, FY in [RES])

UF Horizontal component of ﬂuid velocity, u

,m/s

VF Vertical component of ﬂuid velocity, v

,m/s

WR Speed of ﬂuid relative to body, w

,m/s

CD Drag coefﬁcient of a sphere

48 FLOW TOPICS GOVERNED BY ORDINARY DIFFERENTIAL EQUATIONS

List of Principal Variables in Program 1.5 Maximum Range of a Spherical Projectile

Program Symbol Deﬁnition

DELTA Increment δ in half - interval method, deg

EPSLON ε, used to control the accuracy of the optimum shooting angle, deg

M A counter for different wind conditions

N Number of steps used in the half-interval method

THENEW, THEOLD (θ

)

new

and (θ

)

old

, respectively, deg

THETA Optimum shooting angle at which range is maximum, deg

XP, XQ, YP, YQ x

, x

, y

,and y

, respectively, m

XRMAX Maximum range, m

XRNEW, XROLD (x

)

new

and (x

)

old

, respectively, m

TABLE 1.A.1 Program 1.5 Output

CONSIDER A STEEL SPHERICAL PROJECTILE OF 0.01 M DIAMETER

SHOOTING IN AIR WITH AN INITIAL SPEED OF 50M/SEC.

SYMBOLS USED IN THE FOLLOWING TABLE ARE ;

UF = HORIZONTAL WIND SPEED

THETA = THE OPTIMUM SHOOTING ANGLE

XRMAX=THEMAXIMUMRANGE

N = NUMBER OF STEPS USED IN HALF-INTERNAL METHOD TO

OBTAIN THE PRINTED RESULT

THE ERROR IN THETA IS OF THE ORDER OF 0.001DEGREES.

--------------------------------------------------------------

UF THETA XRMAX N

(M/SEC) (DEG) (M)

--------------------------------------------------------------

2.0000e+01 4.4611e+01 1.8976e+02 2.4000e+01

0 3.9745e+01 1.3020e+02 2.3000e+01

-2.0000e+01 2.7371e+01 7.5615e+01 2.6000e+01

ROLLING UP OF THE TRAILING VORTEX SHEET BEHIND A FINITE WING 49

List of Principal Variables in Program 1.6 Flight Paths of a Glider

Program Symbol Deﬁnition

A Ratio of initial lift to weight of the glider

B Ratio of drag to lift of the glider

DT Dimensionless time increment

F1, F2 Right-hand sides of (1.6.4) and (1.6.5),

respectively

M A counter for changing angle θ

N A counter for time steps

PI π

T Dimensionless time

THETA0 Initial angle between ﬂight path and x-axis, θ

radians

U, U0 Dimensionless horizontal velocity of glider and

its initial value, respectively

V, V0 Dimensionless vertical velocity of glider and

its initial value, respectively

W0 Dimensionless initial velocity of glider

X, Y Coordinates of glider

X1, Y1 Coordinates of glider for θ

=−90

◦

X2, Y2 Coordinates of glider for θ

= 180

◦

INVISCID FLUID FLOWS

All the problems in this chapter are concerned with ﬂows in the absence of

viscosity. The justiﬁcation for ignoring viscosity and a brief review of incom-

pressible irrotational ﬂows can be found in Section 2.1. The numerical solution

of boundary-value problems involving linear second-order ordinary differential

equations is taken up in Section 2.2, and its application to a radial ﬂow is dis-

cussed in Section 2.3.

To solve the problem of ﬂow past a body, two different approaches may be

taken. Bodies of various shapes can be generated either by superimposing ele-

mentary ﬂows or by transforming from known ﬂow patterns using the conformal

mapping technique. These inverse methods are described in Sections 2.4 and 2.6,

respectively. On the other hand, direct methods are used to solve for the ﬂow

around a body of prescribed shape. The von Karman method, in which singu-

larities are placed along the centerline of an axisymmetric body is introduced in

Section 2.5.

The following six sections deal speciﬁcally with the second-order partial dif-

ferential equations with two independent variables. These equations are ﬁrst

classiﬁed in Section 2.7. Numerical methods are devised in Section 2.8 for solving

elliptic equations, and their computational stabilities are examined. An example

is shown to compute the ﬂow induced by a concentrated vorticity in a rectan-

gular domain. In Section 2.9, techniques for handling irregular and derivative

boundary conditions are illustrated. The numerical solution of linear hyperbolic

equations and its stability criterion are considered in Section 2.10, and an appli-

cation to solve the problem of propagation and reﬂection of a sound wave is

given in Section 2.11. The propagation of a ﬁnite-amplitude wave is studied in

Section 2.12 using a numerical scheme constructed for solving nonlinear hyper-

bolic equations. Finally, in Section 2.13, we present a formulation of blood ﬂow

An Introduction to Computational Fluid Mechanics by Example Sedat Biringen and Chuen-Yen Chow

INCOMPRESSIBLE POTENTIAL FLOWS 51

in elastic arteries modeled by a system of nonlinear hyperbolic partial differen-

tial equations. We also introduce multistep methods for numerically integrating

hyperbolic partial differential equations.

2.1 INCOMPRESSIBLE POTENTIAL FLOWS

Real ﬂuids are all viscous. Viscosity is caused by the redistribution of excessive

momenta among neighboring ﬂuid molecules through the action of intermolecular

collisions. Thus, a viscous force is exerted on the surface of a ﬂuid element where

a local velocity gradient is present. It may be either a shearing force tangent to

the surface, such as the one found in a boundary layer, or a normal force that

exists, for example, within a shock wave.

The importance of the viscous force in comparison with the inertial force is

represented by the Reynolds number, which is the ratio of a characteristic inertial

force to a characteristic viscous force in a ﬂow ﬁeld. Because of the low viscosity

of air and water, the Reynolds numbers of most ﬂows of practical interest are

usually very high; in other words, in these ﬂows the viscous forces are very small

compared with the inertia.

For a high-Reynolds number ﬂow past a streamlined body from which the

ﬂow does not separate, Prandtl (1904) postulated that the inﬂuence of viscosity

is conﬁned to a very thin boundary layer in the immediate neighborhood of

the solid wall, and that in the region outside of the boundary layer the ﬂow

behaves as if there were no viscosity. Prandtl’s postulation has been proven to

be a powerful tool in solving many practical ﬂow problems. For instance, the

inviscid ﬂow theory predicts extremely well the lift and pressure distribution on

an airfoil for angles of attack below the value at which the ﬂow starts to separate

from the body, although the drag has to be found by solving the boundary-layer

equations.

It is known that vorticities are generated by the shearing viscous forces, so that

the boundary-layer ﬂow is a rotational one. On the other hand, in the absence of

viscous and other rotational forces, the originally irrotational ﬂow far upstream

will remain so in the region outside the boundary layer. Letting V denote the

velocity ﬁeld in this region, the irrotationality condition states that the vorticity

vanishes; that is,

∇ × V = 0 (2.1.1)

The preceding equation is automatically satisﬁed if a velocity potential φ is

introduced such that

V = ∇φ (2.1.2)

For this reason irrotational ﬂows are also called potential ﬂows.Asaresult

of introducing the velocity potential, the velocity vector generally having three

components is replaced by a single scalar quantity φ.