Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

523.1 The Macroscopic Mass Balances

737

SOLUTION

tering fluid moves through in plug flow (a plug flow reactor, PFR), and another that acts as a

perfect mixer (or continuous stirred tank reactor, CSTR). As shown in Fig. 23.1-7, the responses

to a pulse input are quite different for the PFR and the CSTR. Assume steady flow at a volu-

metric flow rate Q through each system, and further assume that the tracer being followed is

too dilute to affect the flow behavior of the carrier solvent. Assume that no reaction is occurring.

For both systems we assume that the concentration is initially zero throughout and that the

concentration of species

in the inlet stream is

exp(- t/to)

(23.1 -60)

where p, and t, are constants, specific to the problem.

For the PFR, the exit stream concentration shows only a time delay and decay, and we

may write at once for

p,/po

0 for t

t,,, (23.1-61)

where t,,,

V/Q is the mean solute residence time, a second time constant imposed on the sys-

tem. The result for longer time is

which is of more interest to us here.

For the CSTR we begin with the basic differential equation

with the initial condition that

at t

This first-order linear differential equation has

the solution

in which

to/t,,, and

t/to. Exit concentrations are plotted in Fig. 23.1-8 as functions of

the dimensionless time

t/t, for each reactor and for

l/a

t,,,/to of 0.1 and 1.0.

It may be seen that for

l/a

t,,,/t,

1.0

the two reactors produce much different efflu-

ent concentrations, as one might expect. However, for t,,,/to

and t significantly greater

than t,,,, the effluent curves for the two reactors are virtually indistinguishable. This is the re-

gion of validity for compartmental analysis, and we see that in addition to the time constants

imposed by the system itself, there is also another time constant

tabs,

the time at which the ob-

PFR

Fig.

23.1-8.

Response of the

PFR

and the CSTR to an exponentially

decaying input.

738

Chapter

Macroscopic Balances for Multicomponent Systems

servations of the effluent concentration begin. We may then define the range of validity of

compartmental analysis by the inequalities

Thus, compartmental analysis is most useful as a long-time approximate description of a sys-

tem that responds slowly relative to solute residence times of its component units. It may im-

mediately be seen that these conditions are met

Example 23.1-4, where the long-time

metabolite concentrations are of primary interest.

Equation 23.1-66 summarizes the requirements for pharmacokinetics, which are met in a

very wide variety of biological transport-reaction problems. They are also satisfied in a great

many environmental situations.'

523.2 THE MACROSCOPIC MOMENTUM AND

ANGULAR MOMENTUM BALANCES

The macroscopic statements of the laws of conservation of momentum and angular mo-

mentum for a fluid mixture, with gravity as the only external force, are

These (seldom used) equations are the same as Eqs. 7.2-2 and 7.3-2, except for the addi-

tion of the terms

and To, which are the net influxes' of momentum and angular mo-

mentum into the system by mass transfer. For most mass transfer processes these terms

are so small that they can be safely neglected.

523.3 THE MACROSCOPIC ENERGY BALANCE

For a fluid mixture, the macroscopic statement of the law of conservation of energy is

This equation is the same as

Eq.

15.1-2, except that an additional term Qo has been

added.' This term accounts for addition of energy to the system as a result of mass trans-

H. Shair and

Heitner,

Envir. Sci. and

Tech.,

8,444-451 (1974).

These terms may be written as integrals,

pw]

dS;

pw]]

(23.2-1

a, b)

in which

is the outwardly directed unit normal vector.

This term may be written as an integral,

in which n is the outwardly directed unit normal vector. The origin of this term may be seen by referring

Eq.

19.3-5 and

Eq.

(H)

Table 17-8-1.

s23.5

Use of the Macroscopic Balances to Solve Steady-State Problems

739

fer. It may be of considerable importance, particularly if material is entering through the

bounding surface at a much higher or lower temperature than that of the fluid inside the

flow system, or if it reacts chemically in the system.

When chemical reactions are occurring, considerable heat may be released or ab-

sorbed. This heat of reaction is automatically taken into account in the calculation of the

enthalpies of the entering and leaving streams (see Example 23.5-1).

In some applications, in which the energy transfer rates across the surface are func-

tions of position, it is more convenient to rewrite Eq. 23.3-1 in the d-form-that is, over a

differential portion of the flow system as described in 915.4. Then the increment of heat

added, dQ, is expressible in terms of a local heat transfer coefficient.

523.4

THE MACROSCOPIC MECHANICAL ENERGY BALANCE

careful examination of the derivation of the mechanical energy balance in

g7.8

shows

that the result obtained there applies to mixtures as well as to pure fluids. If we now in-

clude the surface

So,

then we get

This is the same as Eq. 7.4-2, except for the addition of the term

B,,

which accounts for

the mechanical energy transport across the mass transfer boundary.' The use of this

equation is illustrated in Example 22.5-3.

823.5

USE OF

THE

MACROSCOPIC BALANCES

TO SOLVE STEADY-STATE PROBLEMS

The macroscopic balances are summarized in Table 23.5-1 for systems with more than

one entry and exit plane. The terms with subscript

describe the addition or removal

of mass, momentum, angular momentum, energy, and mechanical energy at mass-

transfer surfaces. Usually these balances are not used in their entirety, but it is conve-

nient to have a complete listing of them for problem-solving purposes. For steady-state

problems, the left sides of the equations may be omitted. As we saw in Chapters

and

15, considerable intuition is required in using the macroscopic balances, and some-

times it is necessary to supplement the equations with experimental observations.

EXAMPLE

23.5-1

Energy

Balances for a

Sulfur Dioxide

Converter

Hot gases from a sulfur burner enter a converter, in which the sulfur dioxide present is to be

oxidized catalytically to sulfur trioxide, according to the reaction SO2

;o,

SO3. How

much heat must be removed from the converter per hour to permit a 95% conversion of the

SO, for the conditions shown in Fig. 23.5-I? Assume that the converter is large enough for the

components of the exit gas to be

thermodynamic equilibrium with one another. That is, the

partial pressures of the exit gases are related by the equilibrium constraint

In terms

a surface integral, this term is given

740

Chapter

Macroscopic Balances for Multicomponent Systems

Table

23.5-1 Unsteady-State Macroscopic Balances for Nonisothermal

Multicomponent Systems

Mass

species

%,tot

Zw.1

Zw,,

w,,

r.tot

1.2,3,.

Momentum:

Angular momentum:

Mechanical energy:

(Total) energy:

Notes:

(a)

Bw,,

w,,,

walb

wale

. .

where

w,,,

p,,,v,,S,,,

and so on; Equations (A) and

(B)

can be written

in molar units by replacing the lowercase symbols by capital letters and adding to Eq. (A) the term

Z,R,,t,,

account for the fact that moles need not be conserved in a chemical reaction.

(b)

and

are elevations above an arbitrary datum plane.

(c)

and

are enthalpies per unit mass (for the mixture) relative to some arbitrarily chosen reference

state; see Example 19.3-1.

(d) All equations are written for compressible flow; for incompressible flow,

0. The quantities

and

are defined in Eqs. 7.3-3 and 4.

(e)

and

are unit vectors in the direction of flow.

T2=?

c----,

1-00 atm

SO3-rich gas

(;==

Coolant out

.-/'

SO,, 7.80 lb-moles hr-'

02,

10.80 lb-moles hr-I

N2, 81.40 lb-moles

hr-'

Converter

Coolant

440°C

1.05 atm

Fig.

23.5-1. Catalytic oxidation

of sulfur dioxide.

523.5 Use of the Macroscopic Balances to Solve Steady-State Problems

741

SOLUTION

Approximate values of

for this reaction are

It is convenient to divide this problem into two parts:

(a)

first we use the mass balance and

equilibrium expression to find the desired exit temperature, and then

(b)

we use the energy

balance to determine the required heat removal.

(a)

~etermination' of

T,.

We begin by writing the steady-state macroscopic mass balance,

Eq. 23.1-3, for the various constituents in the two streams in the form:

In addition, we take advantage of the two stoichiometric relations

We can now get the desired molar flow rates through surface 2:

Next, substituting numerical values into the equilibrium expression

Eq.

23.5-1 gives

This value of

corresponds to an exit temperature

of about 510°C, according to the equi-

librium data given above.

(b)

Calculation

the required heat removal.

As indicated by the results of Example 15.3-1,

changes in kinetic and potential energy may be neglected here in comparison with changes in

enthalpy. In addition, for the conditions of this example, we may assume ideal gas behavior.

Then, for each constituent,

~I,(T).

We may then write the macroscopic energy balance,

Eq. 23.3-1, as

For each of the individual constituents we may write

H",

Here

H",

is the standard enthalpy of formation2 of species

from its constituent elements

at the enthalpy reference temperature

To,

and

(C,,),,,

is the enthalpy-mean heat capacityz

of the species between

and

To.

For the conditions of this problem, we may use the

See

Hougen,

Watson, and

Ragatz,

Chemical

Process

Principles,

Part II,2nd edition,

Wiley, New York (1959),

pp.

1017-1018.

See, for example,

Hougen,

Watson, and

Ragatz,

Chemical Process Principles,

Part

2nd edition, Wiley, New York (19591,

pp.

257,296.

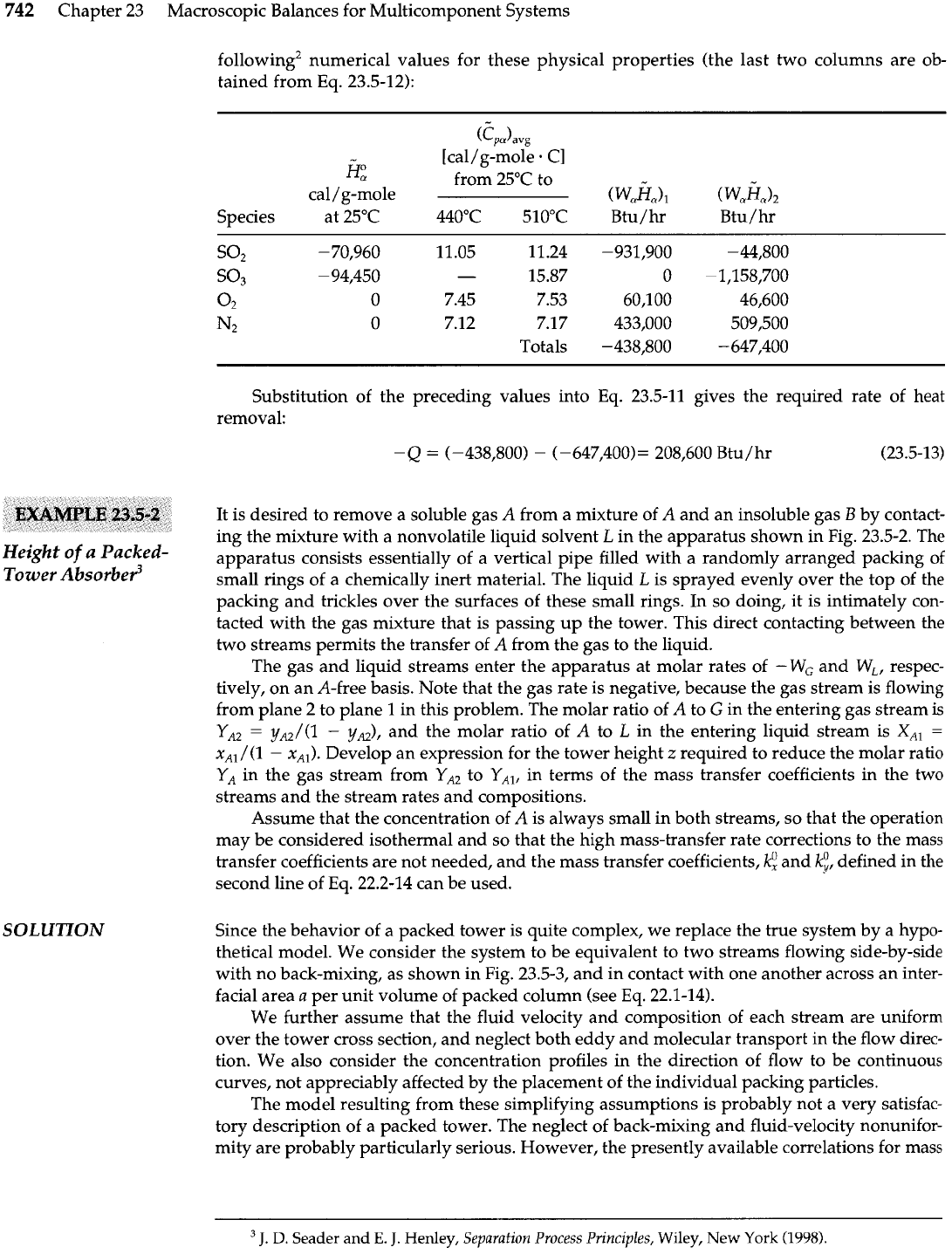
742

Chapter 23 Macroscopic Balances for Multicomponent Systems

EXAMPLE

23.5-2

Height of

Packed-

Tower ~bsorber?

SOLUTION

following2 numerical values for these physical properties (the last two columns are ob-

tained from Eq. 23.5-12):

[~al/~:more. Cl

H::

from 25°C to

cal/g-mole

(w,H,),

(

w,H,),

Species at 25°C 440°C 510°C Btu/hr Btu/hr

SO2

70,960

.05 11.24 -931,900 -44,800

SO3 -94,450

15.87 0 1,158,700

0 7.45 7.53 60,100 46,600

0 7.12 7.17 433,000 509,500

Totals -438,800

647,400

Substitution of the preceding values into Eq. 23.5-11 gives the required rate of heat

removal:

It is desired to remove a soluble gas

from a mixture of

and an insoluble gas

by contact-

ing the mixture with a nonvolatile liquid solvent

in the apparatus shown in Fig. 23.5-2. The

apparatus consists essentially of a vertical pipe filled with a randomly arranged packing of

small rings of a chemically inert material. The liquid

is sprayed evenly over the top of the

packing and trickles over the surfaces of these small rings. In so doing, it is intimately con-

tacted with the gas mixture that is passing up the tower. This direct contacting between the

two streams permits the transfer of

from the gas to the liquid.

The gas and liquid streams enter the apparatus at molar rates of

and W,, respec-

tively, on an A-free basis. Note that the gas rate is negative, because the gas stream is flowing

from plane 2 to plane

in this problem. The molar ratio of

in the entering gas stream is

YA2

yA2/(1

yA2),

and the molar ratio of

in the entering liquid stream is

X,,

xAl/(l

xAl). Develop an expression for the tower height

required to reduce the molar ratio

in the gas stream from

YA2

Y,,,

in terms of the mass transfer coefficients in the two

streams and the stream rates and compositions.

Assume that the concentration of A is always small in both streams, so that the operation

may be considered isothermal and so that the high mass-transfer rate corrections to the mass

transfer coefficients are not needed, and the mass transfer coefficients,

and

k!,

defined in the

second line of Eq. 22.2-14 can be used.

Since the behavior of a packed tower is quite complex, we replace the true system by a hypo-

thetical model. We consider the system to be equivalent to two streams flowing side-by-side

with no back-mixing, as shown in Fig. 23.5-3, and in contact with one another across an inter-

facial area

per unit volume of packed column (see Eq. 22.1-14).

We further assume that the fluid velocity and composition of each stream are uniform

over the tower cross section, and neglect both eddy and molecular transport in the flow direc-

tion. We also consider the concentration profiles in the direction of flow to be continuous

curves, not appreciably affected by the placement of the individual packing particles.

The model resulting from these simplifying assumptions is probably not a very satisfac-

tory description of a packed tower. The neglect of back-mixing and fluid-velocity nonunifor-

mity are probably particularly serious. However, the presently available correlations for mass

Seader and

Henley,

Separation

Process Principles,

Wiley,

New

York

(1998).

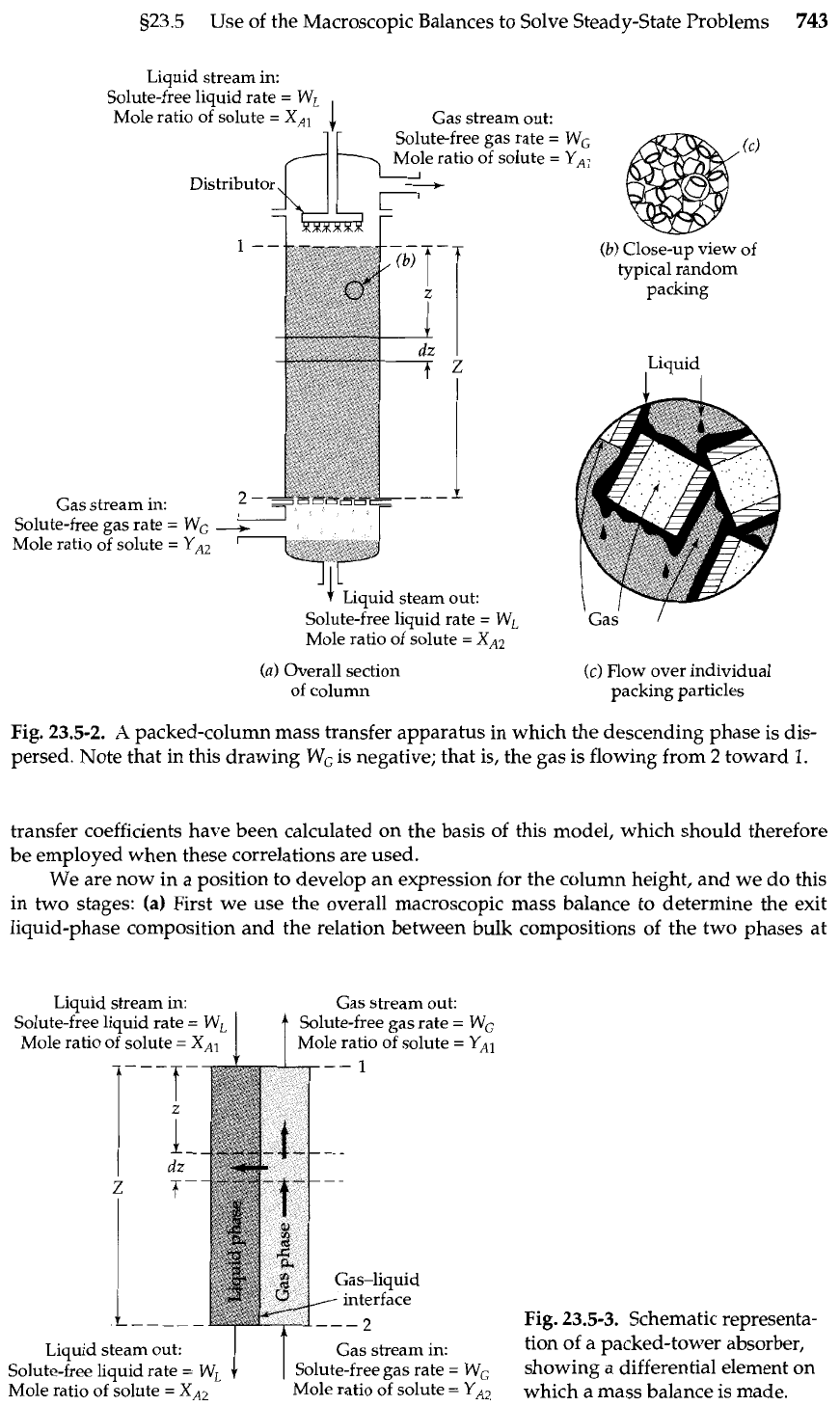
523.5

Use of the Macroscopic Balances to Solve Steady-State Problems

743

Liquid stream in:

Solute-free liquid rate

Mole ratio of solute

Xal

Gas stream out:

Solute-free gas rate

Mole ratio of solute

YAl

Distributor

Gas stream in:

Solute-free gas rate

Mole ratio of solute

YA2

'/'Liquid steam out:

Solute-free liquid rate

Mole ratio of solute

XA2

(a)

Overall section

of column

(b)

Close-up view of

typical random

packing

(c)

Flow over individual

packing particles

Fig.

23.5-2.

packed-column mass transfer apparatus in which the descending phase is dis-

persed. Note that in this drawing

is negative; that is, the gas is flowing from

toward

transfer coefficients have been calculated on the basis of this model, which should therefore

be employed when these correlations are used.

We are now in a position to develop an expression for the column height, and we do this

in two stages:

(a)

First we use the overall macroscopic mass balance to determine the exit

liquid-phase composition and the relation between bulk compositions of the two phases at

Liquid stream in:

Gas stream out:

Solute-free liquid rate

Solute-free gas rate

Mole ratio of solute

XAl

Mole ratio of solute

YAl

Liquid steam out:

Gas stream in:

Solute-free liquid rate

Solute-free gas rate

Mole ratio of solute

XA2

Mole ratio of solute

YA2

Fig.

23.5-3.

Schematic representa-

tion of a packed-tower absorber,

showing a differential element on

which

mass balance is made.

744

Chapter 23 Macroscopic Balances for Multicomponent Systems

each point in the tower.

(b)

We then use these results along with the differential form of the

macroscopic mass balance to determine the interfacial conditions and the required tower

height.

(a)

Overall macroscopic mass balances.

For the solute A we write the macroscopic mass bal-

ance of Eq. 23.1-3 for each stream of the system between planes

and

liquid

stream

gas stream

Here the subscripts A1 and Ag refer to the solute A in the liquid and gas streams, respectively.

Since the number of moles leaving the liquid stream must enter the gas stream across the in-

terface, WAlr0

W,,,,, and Eqs. 23.5-14 and 15 may be combined to give

This can now be rewritten in terms of the compositions of the entering and leaving streams by

setting WAl2

WLXA2, and so on, and then rearrangement gives

Thus we have found the concentration of

in the exit liquid stream.

By replacing plane 2 by a plane at a distance

down the column, Eq. 23.5-17 may be used

to obtain an expression relating bulk stream compositions at any point in the tower:

Equation 23.5-18 (the "operating line") is shown in Fig. 23.5-4 along with the equilibrium dis-

tribution for the conditions of Problem 23A.2.

(b)

Application of the macroscopic-balances

the d-form.

We now apply Eq. 23.1-3 to a dif-

ferential increment

of the tower, first to estimate the interfacial conditions and then deter-

mine the tower height required for a given separation.

(i)

Determination of interfacial conditions.

Because only

is transferred across the in-

terface, we may write, according to the second line of Eq. 22.1-14 (which presumes

low concentrations of A and small mass-transfer rates):

Here

is the interfacial area per unit volume of the packed bed tower,

is the cross-

sectional area of the tower,

XAO

and yAO are the interfacial mole fractions of A in the

liquid and gas phases, respectively, and xA and

are the corresponding bulk con-

centrations (the index

is being omitted here, so that XA,

yA,

XA, and

are all bulk

compositions).

Then, since (for the dilute solutions considered here) xA

XA/(XA

and yA

YA/(YA

YA,

Eqs. 23.5-19 and 20 may be combined to give

This equation enables us to determine

YAO

as a function of

YA.

For any

YA,

one may

locate XA on the operating line (mass balance). One then draws a straight line of

slope -(@a)/($a) through the point

(YA,

XA), as shown in Fig. 23.5-4. The intersec-

tion of this line with the equilibrium curve then gives the local interfacial composi-

tions

(YAO,

XAO).

523.5 Use of the Macroscopic Balances to Solve Steady-State Problems

745

Fig.

23.5-4.

Calculation of interfacial conditions in the absorption of

cyclohexane from air in a packed column (see Problem 23A.2).

(ii)

Determination of required column height.

Application of Eq. 23.1-1 to the gas

stream in

volume

dz of the tower gives

WG~YA

~WA,O (23.5-22)

This expression may be combined with Eq. 23.5-20 for the dilute solutions being

considered to obtain

WGdYA

(kyOa)(YA

YAO)S dz

(23.5-23)

This equation may now be rearranged and integrated from

Equation 23.5-24 is the desired expression for the column height required to effect the speci-

fied separation. In writing Eq. 23.5-24 we have neglected the variation of the mass transfer co-

efficient

with composition. This is usually permissible only for dilute solutions.

In general, Eq. 23.5-24 must be integrated by numerical or graphical procedures. How-

ever, for dilute solutions, it may frequently be assumed that the operating and equilibrium

lines of Fig. 23.5-4 are straight.

If,

in addition, the ratio

@/k;

is constant, then

Y,,

varies

linearly with Y,. We may then integrate Eq. 23.5-24 to obtain (see Problem 23B.1)

where

Equation 23.5-25 can be rearranged to give

746

Chapter

Macroscopic Balances for Multicomponent Systems

Comparison of Eq.

23.5-27

and Eq.

15.4-15

shows the close analogy between packed towers

and simple heat exchangers. Expressions analogous to Eq.

23.5-24

but containing the overall

mass transfer coefficient

may also be derived (see Problem

23B.1).

Again, we may use the

final results, Eqs.

23.5-25

27,

for either cocurrent or countercurrent flow. Keep in mind,

however, that the simplified model used to describe the packed tower is not as reliable as the

corresponding one used for heat exchangers.

EXAMPLE

23.5-3

Linear

Cascades

We saw in Example

23.1-2

that the degree of separation possible in a simple binary splitter

can be quite limited, and it is therefore often desirable to combine individual splitters in

countercurrent cascade such as that shown in Fig.

23.5-5.

Here the feed to any splitter stage

the sum of the waste stream from the splitter immediately above it and the product from the

splitter immediately below.

Show how such an arrangement can increase the degree of separation relative to that ob-

tained in a single splitter.

SOLUTION

For the system as a whole we can write a mass balance for the desired product and for the so-

lution as a whole. That is, we treat the entire system as a splitter and write

It will be assumed here that all of quantities in these equations are given, so that the problem

is specified as far as the overall mass balances are concerned. It remains for us to determine

the number of stages required to meet these conditions.

We begin by writing a set of mass balances over the top portion of the column, here the

top two stages for illustrative purposes (see Fig.

23.5-5):

Here

and

are the upflowing and downflowing streams from stage n, and

and

x,,

are

the corresponding mole fractions of the desired solute. When

is eliminated between Eqs.

23.5-3

and

31,

we get

This equation gives the relation between the compositions of the downflowing and upflowing

streams passing each other at any column cross section above the feed stage, in terms of the cor-

responding flow rates. This relation, when shown on an

x-y

plot (which

called a McCabe-Tkiele

diag~arn~,~) is known as the operating line for the system. We concentrate for the moment on com-

positions and return later to the problem of determining stream rate ratios.

F$4

Fig.

23.5-5.

linear cascade. Upward flows are shown by solid

lines, and downward flows by dashed lines.

McCabe

and

Thiele,

Ind.

Eng.

Chem.,

17,605411

(1925).