Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

523.5

Use of the Macroscopic Balances to Solve Steady-State Problems

747

The phase compositions in each stage are assumed to satisfy an equilibrium relation such

as (see Eq. 23.1-19)

or, more generally,

y,,

(xJ,

where

(x)

is taken to be a known function.

Equations 23.5-32 and 33 (or its generalization) now permit determination of all composi-

tions in the portion of the column above the feed point, usually known as the rectifying section,

and similar calculations can be made for the stripping section, the portion below the feed point.

We may then determine the number

stages required for the separation under consideration

and the proper location of the feed stage.

First, however, we need to determine the stream rate ratios required in Eq. 23.5-32, and

we consider three special cases here:

(a)

Total

reflux.

This special mode of operation, in which

and Ware zero, is important, as

it provides the smallest possible number of stages that can yield the desired output composi-

tions. Here

Dn-l

(23.5-34)

for all n, and the operating line is given by

This simple relation holds for all physical systems. The stage compositions are plotted in Fig.

23.5-6 (for a product mole fraction of 0.9 and a waste mole fraction of 0.0, along with an equi-

librium curve of the form of Eq. 23.5-33 with

2.5.

The steplike lines between the equilibrium and operating lines in this figure suggest a

graphical method of determining stage compositions: each "step" between the equilibrium

and operating lines represents an incremental one-component splitter or stage. The diagram

thus suggests that six stages are required for this rather simple separation. However, for the

situation of total reflux and constant relative volatility

it is simplest to recognize that

For the situation pictured in Fig. 23.5-6, we have then

0'9/0'1

log 2.5

log

(m)

log 81

5.796

log 2.5

which is more accurate but virtually equal to the graphical estimate.

0.2

0.4

0.6

0.8

Lower phase mole

fraction,

Fig.

23.5-6.

McCabe-Thiele diagram for

total reflux, with

2.5 and

0.1

0.9.

748

Chapter 23 Macroscopic Balances for Multicomponent Systems

If products are to be withdrawn, it is necessary to calculate the stream-rate ratios, and the

means for doing so vary with the specific operation considered.

(b)

Thermodynamic constraints: adiabatic cascades and minimum reflux.

For most of the

common stagewise operations, stream ratios are determined by thermodynamic constraints,

and these are thoroughly discussed in a wide variety of unit operations texts. We need not re-

peat this readily accessible information here, but we briefly consider distillation, the most

widely used of all, by way of example. In principle, stream ratios in distillation are deter-

mined by assuming adiabatic columns and a set of "enthalpy balances" (see last paragraph of

s15.1) corresponding to the mass balances just introduced.

However, it is very often permissible to assume equal molar heats of vaporizatio_n for the

various species and to neglect "sensible heats" (i.e., the

CpAT

contributions to

AH).

With

these simplifications the stream rates

and

are constants. We may then write for any po-

sition above the feed plate

U= D

and

y,_lU=x,D +ypP

(23.5-39/40)

and below the feed plate

U+

and

x,D

y,, ,U

x,W

(23.5-41/42)

Here the stage indices

and

refer respectively to the upper or rectifying section (above the

feed point) and to the lower or stripping section of the column (below the feed point).

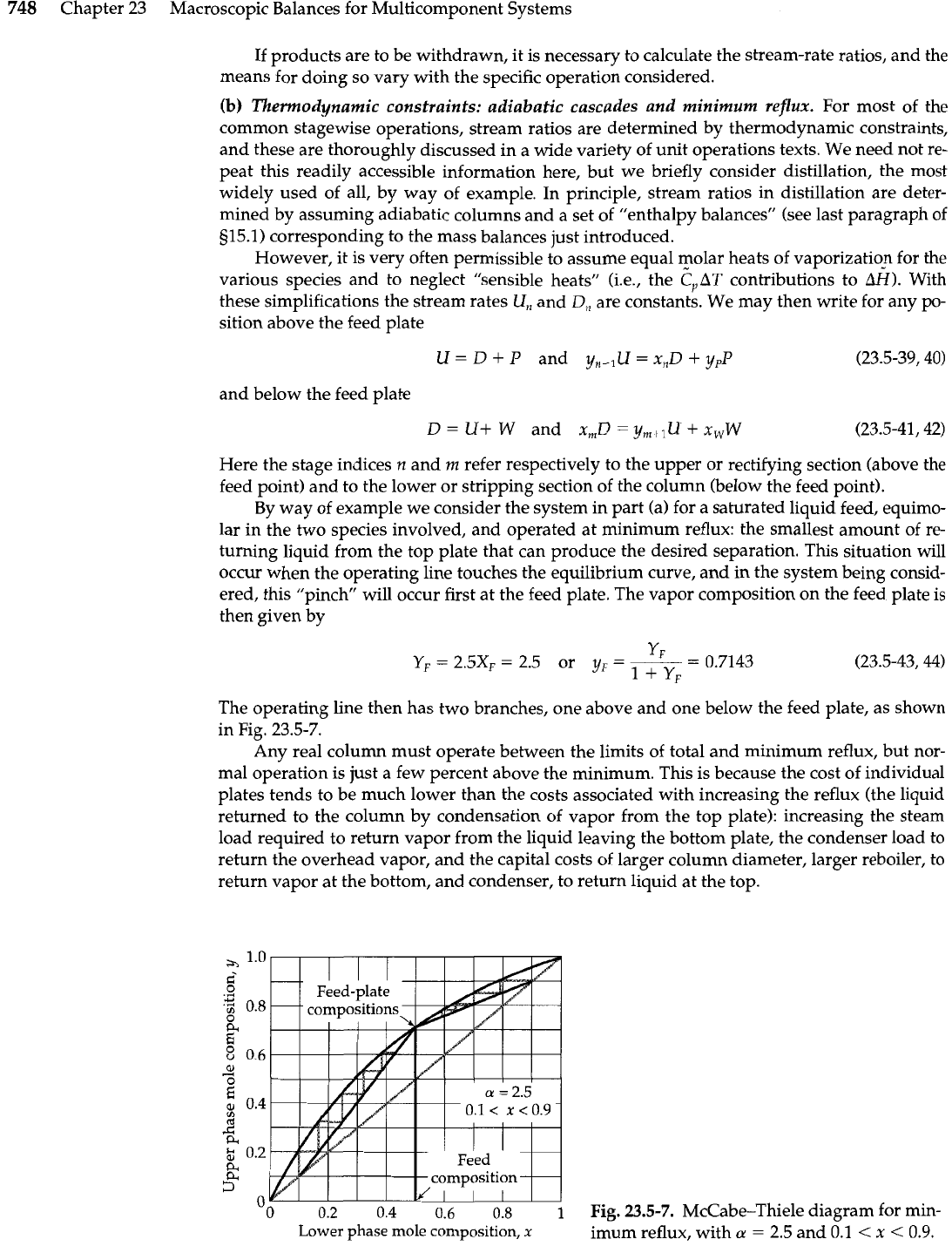
By way of example we consider the system in part (a) for a saturated liquid feed, equimo-

lar in the two species involved, and operated at minimum reflux: the smallest amount of re-

turning liquid from the top plate that can produce the desired separation. This situation will

occur when the operating line touches the equilibrium curve, and in the system being consid-

ered, this "pinch will occur first at the feed plate. The vapor composition on the feed plate is

then given by

The operating line then has two branches, one above and one below the feed plate, as shown

in Fig. 23.5-7.

Any real column must operate between the limits of total and minimum reflux, but nor-

mal operation is just a few percent above the minimum. This is because the cost of individual

plates tends to be much lower than the costs associated with increasing the reflux (the liquid

returned to the column by condensation of vapor from the top plate): increasing the steam

load required to return vapor from the liquid leaving the bottom plate, the condenser load to

return the overhead vapor, and the capital costs of larger column diameter, larger reboiler, to

return vapor at the bottom, and condenser, to return liquid at the top.

0.2

0.4

0.6

0.8

Lower phase mole composition,

Fig.

23.5-7.

McCabe-Thiele diagram for min-

imum reflux, with

2.5 and 0.1

0.9.

g23.5

Use of the Macroscopic Balances to Solve Steady-State Problems

749

0.2 0.4 0.6 0.8

Mole fraction

lower phase,

Fig.

23.5-8.

McCabe-Thiele diagram for an

ideal cascade, with

2.5 and 0.1

0.9.

(c)

Transport constraints and ideal cascades.

For separation via selectively permeable mem-

branes, the ratio of the product to waste streams is governed by the pressure exerted across

the membrane, and the energy required to produce this pressure must be renewed for every

stage of the cascade. This gives the designer an extra degree of freedom and has led to a wide

variety of cascade configurations. First developed for isotopes; membrane cascades have

now been developed for industrial gas separations6 and appear promising for many other

applications.

We consider here by example

ideal

cascades, which are those in which only streams of

identical composition are mixed. In the terms of this example, that means

and, by extension,

It follows that just twice as many stages are needed as at total reflux, and that the operating

line lies halfway between the "equilibrium" curve and the

45"

line. As shown in Fig. 23.5-8,

the operating line has a continuous derivative across the feed stage.

Ideal cascades provide the smallest possible total stage stream flows, but the flows now

vary with position: they are highest at the feed stage and decrease toward the ends of the cas-

cade. For this reason these systems are known as

tapered cascades

(see Problem 23B.6).

An equimolar mixture of CO, and

is confined at lOOOK and 1.50 atm in the large insulated

pressure tank shown in Fig. 15.5-9. Under these conditions the reaction

Expansion

Reactive Gas Mixture

C02

H20

(23.5-47)

ntrough

may take place. After being stored in the tank long enough for the reaction to proceed to equi-

Adiabatic Nozzle

librium, the gas is allowed to escape through the small converging nozzle shown to the ambi-

ent pressure of 1 atm.

von Halle

and

Schacter,

Diffirsion Separation Methods,

Kirk-Othmer Encyclopedia of Chemical

Technology,

Volume

Wiley,

New

York

(1993),

pp.

149-203.

Agrawal,

Ind.

Eng.

Ckem. Research,

35,3607-3617 (1996);

Agrawal and

Xu,

AlChE

Journal,

42,

2141-2154 (1996).

750

Chapter 23 Macroscopic Balances for Multicomponent Systems

SOLUTION

Estimate the temperature and velocity of the escaping gas through the nozzle throat

(a)

assuming that no appreciable reaction takes place during passage of gas through the nozzle,

and

(b)

assuming instant attainment of thermodynamic equilibrium at all points in the nozzle.

In each case, assume that the expansion is adiabatic and frictionless.

We begin by assuming quasi-steady-state operation, flat velocity profiles, and negligible

changes in potential energy. We also assume constant heat capacities and ideal gas behavior,

and we neglect diffusion in the direction of flow. We may then write the macroscopic energy

balance, Eq. 23.3-1, in the form

Here the subscripts

and 2 refer to conditions in the tank and at the nozzle throat, respec-

tively, and, as in Example 15.5-4, the fluid velocity in the tank is assumed to be zero.

To determine the enthalpy change, we equate d(iv2) from the d-form of the steady-state

energy balance (Eq. 23.3-1) to d($v2) of the d-form of the steady-state mechanical energy bal-

ance (Eq. 23.4-1) to get

This result also follows from Eq:

of Table 19.2-4. In addition to Eq. 23.5-49, we use the ideal

gas law and %n expression for

H(T),

obtained with the help of Table 17.1-1, Eq. 19.3-16, and

the relation

ch,

to get

Here

is the mole fraction of the species

at temperature T,and

is the molar enthalpy

species

at the reference temperature

To.

The evaluation of His discussed separately for the

two approximations.

Approximation (a):Assumption of

very

slow chemical reaction.

Here the

are constant

at the equilibrium values for 1000K, and we may write Eq. 23.5-51 as

Hence we may write Eq. 23.5-49 in the form

Since

and

C,,

are assumed constant, this equation may

to get

T (23.5-53)

be integrated from (p,, T,) to (p,,

We may now combine this expression with Eqs. 23.5-48 and 51 to obtain the desired expres-

sion for the gas velocity at plane 2:

523.5

Use of the Macroscopic Balances to Solve Steady-State Problems

751

By substituting numerical values into Eqs. 23.5-54 and 55, we obtain (see Problem 23A.1) T2

920K and

1726 ft/s. It may be seen that this treatment is very similar to that presented in

Example 15.5-4. It is also subject to the restriction that the throat velocity must be subsonic;

that is, the pressure in the nozzle throat cannot fall below that fraction of

required to pro-

duce sonic velocity at the throat (see Eq. 15B.6-2).

the ambient pressure falls below this criti-

cal value of p,, the throat pressure will remain at the critical value, and there will be a shock

wave beyond the nozzle exit.

Approximation

Assumption of ve

rapid reaction. We may proceed here as in part

(a), except that the mole fractions x, must now be considered functions of the temperature de-

fined by the equilibrium relation

and the stoichiometric relations

The quantity

KJT)

in Eq. 23.5-56 is the known equilibrium constant for the reaction. It may be

considered as a function only of temperature, because of the assumed ideal gas behavior and

because the number of moles present is not affected by the chemical reaction. Equations 23.5-

57 and 58 follow from the stoichiometry of the reaction and the composition of the gas origi-

nally placed

the tank.

The expression for the final temperature is now considerably more complicated. For this

reaction, where C.,x,M, is constant, Eqs. 23.5-49 and 50 may be combined to give

where, with the heat capacities approximated as constar~ts,

In general, the integral in Eq. 23.5-60 must be evaluated numerically, since the x, and the

dx,/dT are all complicated functions of temperature governed by Eqs. 23.5-56 to 59. Once T2

has been determined from Eq. 23.5-61, however,

may be obtained by use of Eqs. 23.548

and 51. By substituting numerical values into these expressions, we obtain (see Problem

23B.2) T2

937K and

1752 ft /s.

We find, then, that both the exit temperature and the velocity from the nozzle are greater

when chemical equilibrium is maintained throughout the expansion. The reason for this is

that the equilibrium shifts with decreasing temperature in such a way as to release heat of re-

action to the system. Such a release of energy will occur with decreasing temperature in any

system at chemical equilibrium, regardless of the reactions involved. This is one consequence

of the famous rule of Le Chatelier. In this case, the reaction is endothermic as written and the

equilibrium constant decreases with falling temperature. As a result,

and

H,O

are par-

tially reconverted to

and C02 on expansion, with a corresponding release of energy.

It is interesting that in rocket engines the exhaust velocity, hence the engine thrust, are

also increased if rapid equilibration can be obtained, even though the combustion reactions

are strongly exothermic. The reason for this is that the equilibrium constants for these reac-

tions increase with falling temperature so that the heat of reaction is again released on expan-

sion. This principle has been suggested as a method for improving the thrust of rocket

engines. The increase in thrust potentially obtainable in this way is quite large.

This example was chosen for its simplicity. Note in particular that if a change in the num-

ber of moles accompanies the chemical reaction, then the equilibrium constant, and hence the

enthalpy, are functions of the pressure. In this case, which is quite common, the variables

752

Chapter 23 Macroscopic Balances for Multicomponent Systems

and

implicit in Eq. 23.5-60 cannot be separated, and a step-by-step integration of this equa-

tion is required. Such integrations have been performed, for example, for the prediction of the

behavior of supersonic wind tunnels and rocket engines, but the calculations involved are too

lengthy for here.

523.6

USE OF

THE

MACROSCOPIC BALANCES TO

SOLVE UNSTEADY-STATE PROBLEMS

523.5

the discussion was restricted to steady state. Here we move on to the transient

behavior of multicomponent systems. Such behavior is important in a large number of

practical operations, such as leaching and drying of solids, chromatographic separations,

and chemical reactor operations. In many of these processes heats of reaction as well as

mass transfer must be considered.

complete discussion of these topics is outside the

scope of this text, and we restrict ourselves to several simple examples. More extensive

discussions may be found elsewhere.'

EXAMPLE

23.6-1

Start-up

a Chemical

Reactor

SOLUTION

It is desired to produce

substance

from a raw material

in a chemical reactor of volume

equipped with a stirrer that is capable of keeping the entire contents of the reactor fairly

ho-

mogeneous. The formation of

is reversible, and the forward and reverse reactions may be

considered first order, with reaction-rate constants

kyB

and k;;, respectively. In addition,

un-

dergoes an irreversible first-order decomposition, with a reaction-rate constant kqc, to

third

component

The chemical reactions of interest may be represented as

At zero time, a solution of

at a concentration

cA,

is introduced to the initially empty reactor

at a constant mass flow rate

Develop an expression for the amount of

in the reactor, when it is just filled to its ca-

pacity

assuming that there is no

in the feed solution and neglecting changes of fluid

properties.

We begin by writing the unsteady-state macroscopic mass balances for species

and

molar units these may be expressed

Next we eliminate

MA,tot

from Eq. 23.6-3. First we differentiate this equation with respect to

to get

In this equation, we replace

dMA,tOt/dt

by the right side of

Eq.

23.6-2, and then use Eq. 23.6-3

to eliminate

MArtot.

In this way we obtain a linear second-order differential equation for

M,,,,

as a function of time:

Marshall, Jr., and

Pigford,

The Application of Differential Equations to Chemical Engineering

Problems,

University

Delaware Press, Newark, Del.

(1947);

Ogunnaike and

Ray,

Process

Dynamics, Modeling, and Control,

Oxford University Press

(1994).

s23.6 Use of the Macroscopic Balances to Solve Unsteady-State Problems

753

This equation is to be solved with the initial conditions

This equation can be integrated to give

where

111

2.+

-(k'l:,

kli,

kyc)

kyA

kk',i,

ky;l2

~IB~IC

(23.6-9)

Equations 23.6-8 and

give the total mass of

in the reactor as a function of time, up to the

time at which the reactor is completely filled. These expressions are very similar to the equa-

tions obtained for the damped manometer in Example 7.7-2 and the temperature controller in

Example 15.5-2. It can be shown, however, that

and

are both real and negative, and

therefore

MB,tot

cannot oscillate (see Problem 23B.3).

EXAMPLE

23.62

Unsteady Operation

a Packed Column

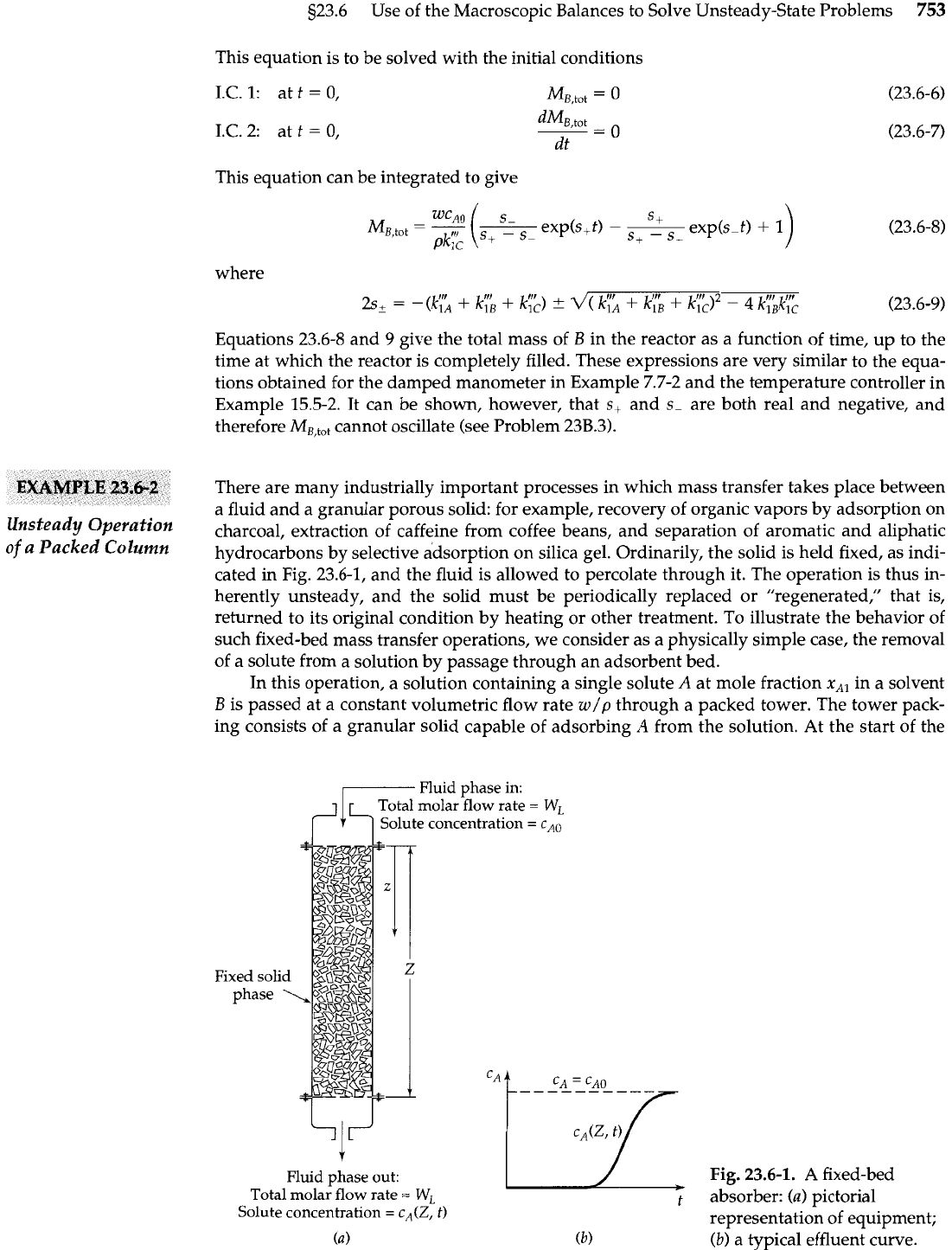
There are many industrially important processes in which mass transfer takes place between

a fluid and a granular porous solid: for example, recovery of organic vapors by adsorption on

charcoal, extraction of caffeine from coffee beans, and separation of aromatic and aliphatic

hydrocarbons by selective adsorption on silica gel. Ordinarily, the solid is held fixed, as indi-

cated in Fig. 23.6-1, and the fluid is allowed to percolate through it. The operation is thus in-

herently unsteady, and the solid must be periodically replaced or "regenerated," that is,

returned to its original condition by heating or other treatment. To illustrate the behavior of

such fixed-bed mass transfer operations, we consider as a physically simple case, the removal

of a solute from a solution by passage through an adsorbent bed.

In this operation, a solution containing a single solute

at mole fraction

x,,

in a solvent

is passed at a constant volumetric flow rate

w/p

through a packed tower. The tower pack-

ing consists of a granular solid capable of adsorbing

from the solution. At the start of the

Fluid phase

in:

Total molar flow rate

Solute concentration

CAO

A-

Fluid phase out:

Total molar

flow

rate

Solute concentration

cA(Z,

(a)

Fig.

23.6-1.

fixed-bed

absorber:

(a)

pictorial

representation of equipment;

(b)

a typical effluent curve.

754

Chapter

Macroscopic Balances for Multicomponent Systems

SOLUTION

percolation, the interstices of the bed are filled with pure liquid

and the solid is free of

The percolating fluid displaces this solvent evenly so that the solution concentration of

always uniform over any cross section. For simplicity, it is assumed that the equilibrium

concentration of

adsorbed on the solid is proportional to the local concentration of

in the

solution. It is also assumed that the concentration of

in the percolating solution is always

small and that the resistance of the porous solid to intraparticle mass transport is negligible.

Develop an expression for the concentration of

in the column as a function of time and

of distance down the column.

Paralleling the treatment of the gas absorber in Example 23.5-2, we think of the two phases as

being continuous and existing side by side as pictured in Fig. 23.6-2. We again define the con-

tact area per unit packed volume of column as

Now, however, one of the phases is station-

ary, and unsteady-state conditions prevail. Because of this locally unsteady behavior, the

macroscopic mass balances are applied locally over a small column increment of height

Az.

We may use

Eq.

23.1-3 and the assumption of dilute solutions to state that the molar rate of

flow of solvent,

WE,

is essentially constant over the length of the column and the time of oper-

ation. We now proceed to use

Eq.

23.1-3 to write the mass conservation relations for species

in each phase for

column increment of height

Az.

For the

solid

phase

in this increment of column we may apply

Eq.

22.3-3 locally, keeping

in mind that now

MA,,,,

depends on both

and

Here use has been made of

Eq.

22.1-14, and the symbols have the following meaning:

volume fraction of column occupied by the liquid

cross-sectional area of (empty) column

c,,

moles of adsorbed

per unit volume of the solid phase

bulk mole fraction of

in the liquid phase

xAo

interfacial mole fraction of

in the fluid phase, assumed to be in equilibrium with

cA,

fluid-phase mass transfer coefficient, defined in

Eq.

22.1-14, for small mass-transfer rates

Fluid

total

molar rate

Fig.

23.6-2.

Schematic model for a fixed-bed absorber,

Fluid

ou;

at total

showing a differential element over which a mass balance

molar rate

is made.

g23.6

Use of the Macroscopic Balances to Solve Unsteady-State Problems

755

Note that, in writing Eq. 23.6-11, we have neglected convective mass transfer through the

solid-fluid interface. This is reasonable

xAO is much smaller than unity. We have also as-

sumed that the particles are small enough so that the concentration of the solution surround-

ing any given particle is essentially constant over the particle surface.

For the

fluid

phase, in the column increment under consideration, Eq. 23.1-3 becomes

Here c is the total molar concentration of the liquid. Equation 23.6-13 may be rewritten by the

introduction of a modified time variable, defined by

It may be seen that, for any position in the column,

is the time measured from the instant

that the percolating solvent "front" has reached the position in question. By rewriting Eqs.

23.6-13 and

in terms of t', we get

Equations 23.6-15 and 16 combine the equations of conservation of mass for each phase with

the assumed mass transfer rate expression. These two equations are to be solved simultane-

ously along with the interphase equilibrium distribution, xAO

mcAsl in which

is a constant.

The boundary conditions are

B.C.

B.C. 2: at

cAs

for all

XA,

for all

Before solving these equations, it is convenient to rewrite them in terms of the following di-

mensionless variables:

In terms of these variables, the differential equations and boundary conditions take the form

with the boundary conditions Y(f; 0)

and X(0,

The solution2 to Eqs. 23.6-23 and 24 for these boundary conditions is

Here JO(ix) is a zero-order Bessel function of the first kind. This solution is presented graphi-

cally in several available

reference^.^

This result was first obtained

A. Anzelius,

Z. angew. Math.

Mech.,

6,291-294 (1926),

for the

analogous problem in heat transfer. One method of obtaining this result is outlined in Problem

23D.1.

See

also H. Bateman,

Partial Differential Equations of Mathematical Physics,

Dover, New York

(19441,

pp.

123-125.

See, for example,

Hougen and

Watson,

Chemical Process Principles,

Part

111,

Wiley, New

York

(1947),

1086.

Their

y/yo,

b~,

and

correspond to

our

and

756

Chapter 23 Macroscopic Balances for Multicomponent Systems

For many complex systems, complete descriptions are either infeasible or unnecessary, and it

is sufficient to obtain only a few basic characteristics. Specifically, we may ask how one may

The

Low-

determine the system volume

and the volume flow rate

through it from observations of

Order Moments

short tracer pulses of mass

introduced at the inlet and then measured at the outlet. Con-

sider for this purpose the macroscopically steady flow through a closed system of arbitrary

geometry, but with a single inlet and outlet, such as that suggested in Fig. 7.0-1, except that

there are no moving surfaces. The flow and diffusional behavior are arbitrary, except that the

tracer distribution must be described by the diffusion equation (Eq. 19.1-7 with Eq. 17.7-3 in-

serted for the mass flux)

in which

is the local tracer concentration and

9Ts

is the pseudobinary diffusivity for the

tracer moving through the solution that fills the system. Turbulent systems may be included

by using time-smoothed quantities and an effective turbulent diffusivity.

In developing the macroscopic balances we shall need to use the condition that there is

no flow or diffusion through the walls of the enclosure

0 and (n

VpT)

0 (23.6-27,281

and that the diffusive flux of the tracer is small compared to the convective flux at the inlet

and outlet to the system

Here

is the outwardly directed unit normal vector. We take the inlet tracer concentration to

be zero up to

0 and also after some finite time

t,.

In practice the concentration pulse

duration should be quite short.

SOLUTION

The analysis4 is based on the moments

I"')

of the tracer concentration with respect to time, de-

fined by:

We now multiply Eq. 23.6-26 by

and integrate with respect to time over the range of

nonzero exit tracer concentration

When the first term is integrated by parts and we make use of the notation introduced in

Eq.

23.6-30, we get

for all systems that give finite moments. We now have a hierarchy of equations for the

I'"'

terms of the lower-order moments, and the structure of these equations is very convenient.

In physical terms, it was first noted by Spalding5 that Eq. 23.6-32 has the same form as the

diffusion equation with chemical reaction, Eq. 19.1-16, but with the concentration replaced

I(")

and the reaction term replaced by

nI'"-~".

Hence we can integrate these equations over the

entire volume of the flow system and thereby develop a new set of macroscopic balances.

Lightfoot,

Lenhoff,

and

Rodrigues,

Chem.

Eng.

Sci.,

36,954-956 (1982).

Spalding,

Chem.

Eng.

Sci.,

9,74-77

(1958).