Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

522.8

Transfer Coefficients at High Net Mass Transfer Rates

707

falling film system is shown in Fig. 22.8-4. The time of travel from the liquid inlet

to the liquid outlet (the "exposure time") is sufficiently short that the diffusing species

does not penetrate very far into the liquid. In such a situation, we can (from a mathemat-

ical point of view) regard the falling film as infinitely thick. We may then take over the

results from Example 20.1-1.

Equation 20.1-23 gives the concentration profiles for a corresponding unsteady-state

system with large net mass transfer rate, and an analogous equation can be written

down for the temperature profiles:

erf(qT

9,)

erf

(0,

rIT

- -

erf p,

Here

y/m

and

y/G

are dimensionless distances from the interface,

and p in each formula is a dimensionless molar average velocity at the interface:

From these results and the definitions for the transfer coefficients in Eqs. 22.8-1 and 2, we

may now get the rate factors

the flux ratios

and the correction factors 0, defined in

the preceding subsection:

From the definitions in Eqs. 22.8-1 and 2 and the profiles in Eqs. 22.8-11 and 12, we can

also get the expressions for the transfer coefficients at low net mass transfer rates:

distance into liquid

film

Liquid

out

Fig.

22.8-4.

Diffusion into a

falling liquid film. Here

tmp

the total time of exposure of a

typical element of volume near

the surface.

708

Chapter 22 Interphase Transport in Nonisothermal Mixtures

The corresponding coefficients at high net mass transfer rates can be obtained by multi-

plying by the correction factor in Eq. 22.8-16.

From the last two equations we get the relation

similar relation, with an exponent of

(instead of

is obtained from the Chilton-Col-

burn relations given in Eqs. 22.3-23 to 25. The latter are valid for flows adjacent to rigid

boundaries, whereas Eq. 22.8-19 pertains to fluid-fluid systems with no velocity gradient

at the interface.

The proportionality of

k,,,,,

to the square root of the diffusivity, given in

Eq.

22.8-17,

has been confirmed experimentally for the liquid phase in several gas-liquid mass trans-

fer systems, including short wetted-wall columns, packed columns, and liquids around

gas bubbles in certain instances. The penetration model has also been applied to absorp-

tion with chemical reactions (see Example 20.1-2).

The Flat-Plate Boundary Layer Model

The steady-state transport in the boundary layer along a flat plate for a fluid with con-

stant physical properties was discussed in g20.2. The eneral expression for the profiles,

n(q, A, K), was given in Eq. 20.2-43. There q

vJ2vx is a dimensionless position co-

ordinate measured from the plate,

is the physical property group (i.e., 1, Pr, or

Sc),

and

(v,/v,)w is a dimensionless net mass flux from the plate.

Once again we introduce the notations defined in Table 22.8-1. Then for the bound-

ary layer calculation we have

In the boundary layer calculation it was assumed that the heat capacities of both species

are identical.

The momentum, heat, and mass fluxes for the flat plate are given in Fig. 22.8-5. Then

in the following two figures, Figs. 22.8-6 and 22.8-7, two plots are given, comparing the

correction factors,

for the film model, the penetration model, and the boundary layer

model. The boundary layer model gives a dependence on

that is not found in the other

models, because this model includes the effect of the tangential velocity profiles on the

temperature and concentration profiles. The film model predicts the smallest depen-

dence of the transfer coefficients on net mass-transfer rate.

Correction factors considerably different from

arise when either

is of mag-

nitude

or greater for

XA;

see Figures 22.8-6, 7 and 8, and the relation

+/R.

Large net interfacial mass fluxes, by these measures, are common when the mass trans-

fer is mechanically driven as in ultrafiltration (Example 22.8-5) and transpiration cooling

(Problem 20B.7(c)). Large net mass fluxes can also occur in vaporization, condensation,

melting and other changes of state, and in heterogeneous chemical reactions, when ac-

companied by correspondingly large temperature differences or radiation intensities to

transfer the requisite latent heat or energy of reaction. More moderate net fluxes, and

correction factors near unity, are common in multistage and packed-column separation

processes, where the differences of temperature and composition within a separation

stage or flow cross-section are normally rather small. The energy flux ratio

is an im-

portant criterion for assessing the net-flux corrections, as illustrated in Examples 22.8-2

and 3.

s22.8

Transfer Coefficients at High Net Mass Transfer Rates

709

l+RforR<O

Asymptote for

-m:

-1

Fig.

22.8-6.

The variation of the

transfer coefficients with mass

transfer rate as predicted by

various models. The line for

holds for the nonsepa-

rated, steady state boundary-

layer regions on rigid surfaces,

whatever their geometry.

0.8

0.6

0.4

141

0.2

0.1

0.08

0.06

0.04

0.02

0.01

1 1 11 11111

11 11111 1 1 1 11 111

0.01 0.02 0.05 0.1 0.2 0.5 1.0 2 5 10 20 50 100

Fig.

22.8-5.

Heat and mass fluxes between a flat plate and a laminar

boundary layer

[W.

Stewart, ScD thesis, Massachusetts Institute of

, , , , , , , , , , , , , , ,

, , , , , , , , ,

For positive R, read positive

from lower curves..-

For negative R, read negative

on upper curves.

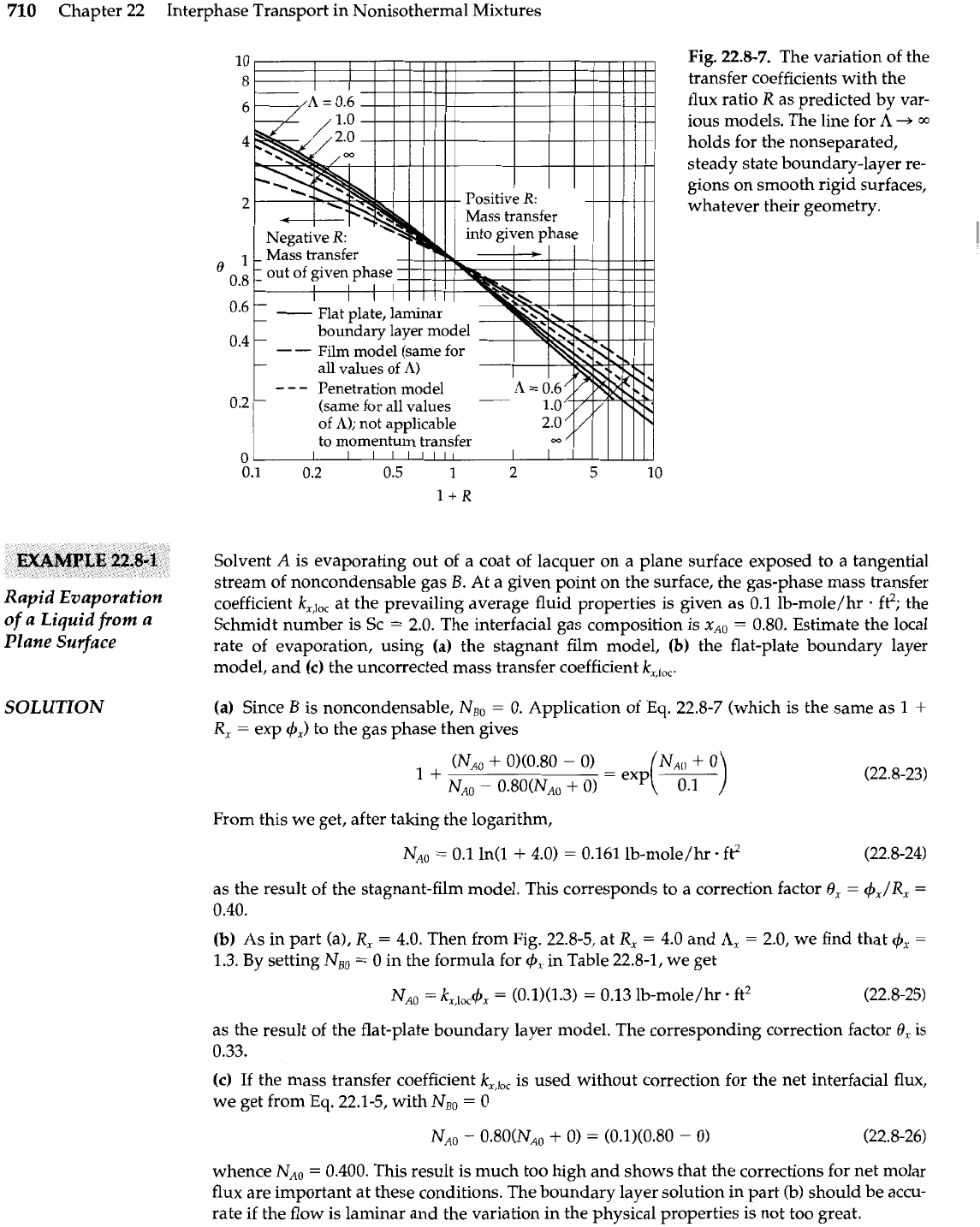
710

Chapter

Interphase Transport in Nonisothermal Mixtures

Fig.

22.8-7.

The variation of the

transfer coefficients with the

flux ratio

as predicted by var-

ious models. The line for

holds for the nonseparated,

steady state boundary-layer re-

gions on smooth rigid surfaces,

whatever their geometry.

EXAMPLE

22.8-1

Rapid Evaporation

Liquid

from a

Solvent

is evaporating out of a coat of lacquer on a plane surface exposed to a tangential

stream of noncondensable gas

At a given point on the surface, the gas-phase mass transfer

coefficient

k,,,,,

at the prevailing average fluid properties is given as 0.1 lb-mole/hr

ft2; the

Schmidt number is Sc

2.0. The interfacial gas composition is

XAO

0.80. Estimate the local

Plane

Surfnce

rate of evaporation, using

(a)

the stagnant film model,

(b)

the flat-plate boundary layer

model, and

(c)

the uncorrected mass transfer coefficient

k,,,,,.

SOLUTION

(a)

Since

is noncondensable,

NBo

0. Application of

Eq.

22.8-7 (which is the same as 1

exp

4,)

to the gas phase then gives

From this we get, after taking the logarithm,

as the result of the stagnant-film model. This corresponds to a correction factor

+,/R,

0.40.

(b)

As in part (a),

4.0. Then from Fig. 22.8-5, at

4.0 and

2.0, we find that

1.3. By setting

NBo

0 in the formula for

in Table 22.8-1, we get

as the result of the flat-plate boundary layer model. The corresponding correction factor

0.33.

(c)

If the mass transfer coefficient

k,,l,,

is used without correction for the net interfacial flux,

we get from

Eq.

22.1-5, with

NBO

whence

NAO

0.400. This result is much too high and shows that the corrections for net molar

flux are important at these conditions. The boundary layer solution in part

(b)

should be accu-

rate if the flow is laminar and the variation in the physical properties is not too great.

g22.8 Transfer Coefficients at High Net Mass Transfer Rates

711

Adjust the results of Example 22.3-1 for the net molar flux by applying the correction factors

and 19, from the film model and from the flat-plate boundary layer model.

Correction Factors in

Droplet Evaporation

SOLUTION

In Example 22.3-3 the molar flux ratio R, at any point on the surface of the drop is

From Eq. 22.8-9 (film model) or Fig. 22.8-7 (flat-plate boundary layer model), the predicted

correction factor

is about 0.99 at all points on the drop. Hence the corrected mass transfer

rate is (by adjustment of Eq. 22.3-31)

This result differs only slightly from that obtained in Example 22.3-1. Thus the assumption of

a small mass-transfer rate was satisfactory under the given conditions.

Extend the analysis of Example 22.3-2 to include the corrections for net mass-transfer rate,

using the stagnant film model.

Wet-Bulb

Performance

Corrected for

ass-

Transfer Rate

SOLUTION

rewriting the energy balance, Eq. 22.3-32, for any point on the wick, we obtain for finite

mass-transfer rate

Multiplication of both sides by CpA/(AiiArVaphioc) gives, since

NAO&

&(T-

To)

RT=~-

bloc

~~A,uap

The right-hand member of this equation is easily calculated if

TO,

T,,

and

are given.

Next we write the expression

r#~

ln(1

R) for both heat and mass transfer, taking into

account the fact that

NBO

Solving both equations for NA, and equating the resulting expressions gives

hloc

In(1

ln(1

R,)

(22.8-33)

kx,locC,A

Then substituting the expressions for R, and RT from Table 22.8-1 yields

This equation shows that

xAo

and

will be constant over the surface of the wick if

h,,/(k&,,,) is constant and thus equal to h,,,/(k,,l<,A). This constancy is assumed here for

712

Chapter 22 Interphase Transport in Nonisothermal Mixtures

EXAMPLE

22.8-4

Comparison of

Film

and Penetration

Models for Unsteady

Evaporation in a

Long Tube

simplicity. Such an assumption is particularly satisfactory for the water-air system, for which

Pr and Sc are nearly equal. With this substitution,

Eq.

22.8-34 becomes

This solution simplifies exactly to Eq. 22.3-35 at low mass-transfer rates.

For the numerical problem in Example 22.3-2, the following values apply:

xAo

0.0247

CPA

8.03 Btu/lb-mole

for water vapor at 105°F

h,/k,,

5.93

Btu/lb-mole

from the Chilton-Colburn analogy (Eq. 22.3-25)

Insertion of these values into Eq. 22.8-35 gives

Solving this equation, we get

x,,

0.0034 (22.8-37)

This result differs only slightly from the value 0.0033 obtained in Example 22.3-2 and justifies

the previous omission of the correction factors under the given conditions.

Numerical studies indicate that the simple

Eq.

22.3-34 gives a close approximation to

Eq.

22.8-35 for the air-water system under all likely wet-bulb conditions. Eqs. 22.3-32 and 33

overestimate the mass transfer rate almost equally, and when these equations are combined,

the errors largely compensate.

Compare the effects of net mass transfer for the unsteady evaporation system described in

Example 20.1-1 with the predictions of

(a)

the generalized penetration model, and

(b)

the

stagnant-film model introduced above. The latter calculation amounts to a quasi-steady-state

treatment of this time-dependent system.

SOLUTION

We begin by noting that for this system

x,,

0 and

N,,

0. It follows from Eq. 22.8-la and

Table 22.8-1 that

The correction factor 8, is thus the ratio of the flux corrected for net mass transfer to the un-

corrected flux.

(a)

The penetration model.

We note that the concentration gradient at the liquid surface can

be obtained by differentiating Eq. 20.1-16 and rewriting the result in terms of

and

The

re-

sult is

2 exp(-q2)

x,,

erf

.\/=

For negligible net mass transfer,

0. Thus, the ratio of the mass flux in the presence of net

mass transfer to the flux in the absence of net mass transfer is

s22.8 Transfer Coefficients at High Net Mass Transfer Rates

713

Table

22.8-2

Comparison of Film and Penetration Models.

8, from penetration model

8, from film model

X~~

(Eq. 22.8-41) (Eq. 22.8-42)

in agreement with Eqs. 22.8-14 and 16. To get

as a function of

x,,,

we may use Fig. 22.8-7, or

use Eq. 20.1-17 to write

xAO)+(xAO) (penetration model) (22.8-41)

where +(xAO) is the quantity defined just after Eq.

20.1-22

and given in Table 20.1-1.

(b)

The stagnant-film model.

The film model result may be obtained from Eq. 22.8-9 in the

form 8

/R) ln(1

R) to obtain

XAO

X~O

lxAO)

(film model)

Numerical values for both models are provided in Table 22.8-2 and also in

Fig.

22.8-7.

It is seen that the penetration model predicts a stronger correction 8, for net mass transfer

than does the film model. This is in part because the net flow thickens the boundary layer, an

effect that the film model does not consider. It may also be noted that this example is a realis-

tic use of the penetration model, as there is little effect of solute concentration on the physical

properties in this simple isothermal system.

much different situation is seen in the next

example.

Ultrafiltration of proteins is a concentration process, in which water from an aqueous protein

solution is forced through a membrane impermeable to the protein but permeable to water

Concentration

and small solutes such as inorganic salts. Protein then accumulates in a polarization layer, or

Polarization in

region of high protein concentration adjacent to the membrane surface, as indicated in Fig.

Ultrafiltration

22.8-8. Determine the relation between water permeation velocity and the transmembrane

Protein

boundary layer

Membrane

Fig.

22.8-8.

spinning-

disk ultrafilter.

714

Chapter 22 Interphase Transport in Nonisothermal Mixtures

SOLUTION

pressure difference. Describe the effect of net mass transfer on the mass transfer coefficient for

protein transport. Assume that the membrane is completely impermeable to protein so that

the net transport of protein across the membrane surface is zero.

For simplicity we choose a spinning-disk geometry as shown in Fig. 22.8-8, for which the pro-

tein concentration will be a function only of the distance

from the disk surface and not of ra-

dial position5 (see Problem 19D.4). However, we will have to consider the dependence of

density, viscosity, and protein-water diffusivity on the protein concentration, and we will

need the concept of osmotic pres~ure.~

The basis for our solution is the concept of

hydraulic permeability

of the filtration

membrane:

Here

is the velocity, or volumetric

flux,

of the solvent leaving the downstream surface of

the membrane. Equation 22.8-43 defines

KH,

the hydraulic permeability of the membrane. The

quantities

and

are the hydrodynamic pressures against the membrane as indicated in

Fig. 22.8-8, and

is the

osmotic pressure

at the upstream surface of the membrane. The inclu-

sion of

.rr

recognizes that it is really the total thermodynamic potential that drives the trans-

membrane transport (this point will be discussed further in Chapter 24.)

For this situation, the interfacial protein velocity is zero, so that a solvent mass balance

across the protein boundary layer gives

in which

is the distance from the upstream membrane surface into the protein boundary

layer. The quantity

p'S'

is the density of the pure solvent, and

pso

PS(y=O

and

vso

vSy(y=O

are

the mass concentration and velocity of solvent at the upstream membrane surface.

The osmotic pressure

?.r

is a function of the protein concentration

p,,

and we will provide

an example of this in Problem 22C.1. We find then that the water flux across the membrane

depends on the protein concentration at the membrane surface as well as the hydrodynamic

pressure drop across the membrane. This concentration, in turn, can be related to

through

the membrane impermeability condition for the protein and the definition of the mass trans-

fer coefficient. Then at

we describe the impermeability of the membrane to protein by

where

k;,

has been defined analogously to

k;..

Combination with

Eq.

22.8-44 then gives

This equation may now be solved for the filtrate velocity:

Here

pp,

pso

and

&/kp

is a mass transfer correction factor, analogous to

O,,

which

now must include the effects of property changes as well as the net velocity correction intro-

duced in Table 22.8-1. We return to a discussion of this quantity below (see

Eq.

22.8-48). The

term

p,,

is the solution density at the upstream membrane surface.

We can now calculate the desired quantities,

and the transmembrane pressure differ-

ence, if we have sufficient information about the transport and equilibrium properties. Here

we consider the approaching protein concentration

pp,

to be given, and for convenience we

Olander,

Heat Transfer,

84,185

(1972).

Silbey and

A. Alberty, Physical Chemistry, 3rd edition, Wiley,

New

York (20011,

206.

522.8 Transfer Coefficients at High Net Mass Transfer Rates

715

begin by selecting values of the protein concentration p,, at the membrane surface over the

range between p,, and the solubility limit of the protein:

(i)

For any chosen value of pp,, we can calculate the corresponding value of

from Eq.

22.8-47 with appropriate values for

and

These values also permit calculation of

osmotic pressure

from the appropriate equilibrium relationship.

(ii)

We may then calculate the transmembrane pressure difference required for this flow

from

Eq.

22.8-43 and an appropriate value of

K,.

The strong effects of protein concentration on system properties mean that the solution must

be obtained numerically.

We content ourselves here to summarize the results of Kozinski and Lightfoot7 for

bovine serum albumin; they were the first to make such calculations and seem still to have

provided the best documentation. In their publications it is shown that the effective mass

transfer coefficient can be expressed as the product of two factors, one accounting for the con-

centration effects and another taking account of the additional effect of property variations:

where, over the parameter space investigated,

and

Equations 22.8-49 to 52 must be considered empirical. Equation 22.8-47 overpredicts

for

small polarization levels, but for that situation the effect of osmotic pressure on flow is small.

The subscript re1 means "relative to the free-stream value."

The mass transfer coefficient in the limit of slow mass transfer and small property varia-

tions is given7 as

v(m)

kpL

0.6205(&)1/2(-)1'3

Sh,

Shl,,

9pJw)

v(a)

%ps(m)

in which

is the disk diameter and

is the rate of rotation in radians per unit time. The inde-

pendence of mass transfer rate on disk size is the reason that this geometry is so popular for

careful mass transfer studies. Other geometries are considered briefly by Kozinski and Light-

A comparison of a priori predictions from the above model with experimental data is

shown in Fig. 22.8-9, where we see that the two agree well. This good agreement may result

in part because the albumin molecules behave much like incompressible particles at the high

solvent ionic strength at which the data were taken. It may also be seen that osmotic effects

are negligible below pressure drops of about 5 psi; here the predicted behavior is indistin-

guishable from that of the protein-free solvent, essentially water. It is only in this unimpor-

tant region that

Eq.

22.8-48 is unreliable. Details of the calculations are provided in Problem

22C.1.

The effect of increasing pressure difference across the protein boundary layer is quite dif-

ferent from that for a nonselective membrane. At first, the concentration boundary layer gets

thinner, as would be expected, and the mass transfer coefficient

increases. However, with

A. A.

Kozinski, PhD thesis, University of Wisconsin (1971);

Kozinski and

Lightfoot,

AIChE

Journal,

18,1030-1040 (1972).

716

Chapter 22 Interphase Transport in Nonisothermal Mixtures

Fig.

22.8-9.

Protein ultrafiltration

with a spinning disk at 273 rpm.

0.1

0.08

0.06

0.04

Transmembrane pressure drop, psi

0.02

further increase in the pressure difference the boundary layer thickness,

and

19,

all approach

asymptotic limits. In practice, these asymptotes are closely approached before the effect of po-

larization becomes appreciable, relative to the membrane flow resistance, and these asymp-

totes suffice to predict the relation between the transmembrane pressure difference and

transmembrane flow.

The behavior can be seen more clearly inserting Eq. 22.8-48 and 49 and the approximate

formula

into Eq. 22.8-47. Then, to a surprisingly good approximation, Eq. 22.8-47 takes the form

The quantity in the first set of parentheses has the form of the simple film model, but with

multiplied by 1.39. It is probably

Eq.

22.8-55 that has made the simple film model attractive to

many for correlating ultrafiltration and reverse osmosis data. However, neglect of the multi-

plier 1.39 has caused corresponding underestimation of

v,,

even before addressing the effects

of property variations.

Bovine serum

albumin, 2.2 g/lOO ml

522.9

MATRIX APPROXIMATIONS FOR MULTICOMPONENT

MASS TRANSPORT

Multicomponent mass transport occurs widely in chemical, physiological, biological,

and environmental processes and is analyzed by various mathematical methods. Here

we review some matrix approximation methods for mass transport by convection and

ordinary diffusion in multicomponent gases.

fuller treatment, including mass trans-

port in liquids, is given in the text by Taylor and Krishna.'

Multicomponent mass transport problems are commonly approximated by lin-

earization-that is,

replacing the variable properties in the governing equations with

constant reference values. This approach is a useful complement to purely numerical

methods, especially for complex flows, and can give good predictions when the property

Taylor and

Krishna,

Multicomponent Mass Transfer,

Wiley,

New

York

(1993).