Bird R.B., Stewart W.E., Lightfoot E.N. Transport Phenomena

Подождите немного. Документ загружается.

522.5 Mass Transfer and Chemical Reactions

697

(i)

For

small values

cB,/c,,, or

for

equal diffusivities,

acgm

Ha=1+-

~CAO

(ii)

For large

values

cBZ/cAO,

(iii)

For all

values

cB,,/cAO (approximate),

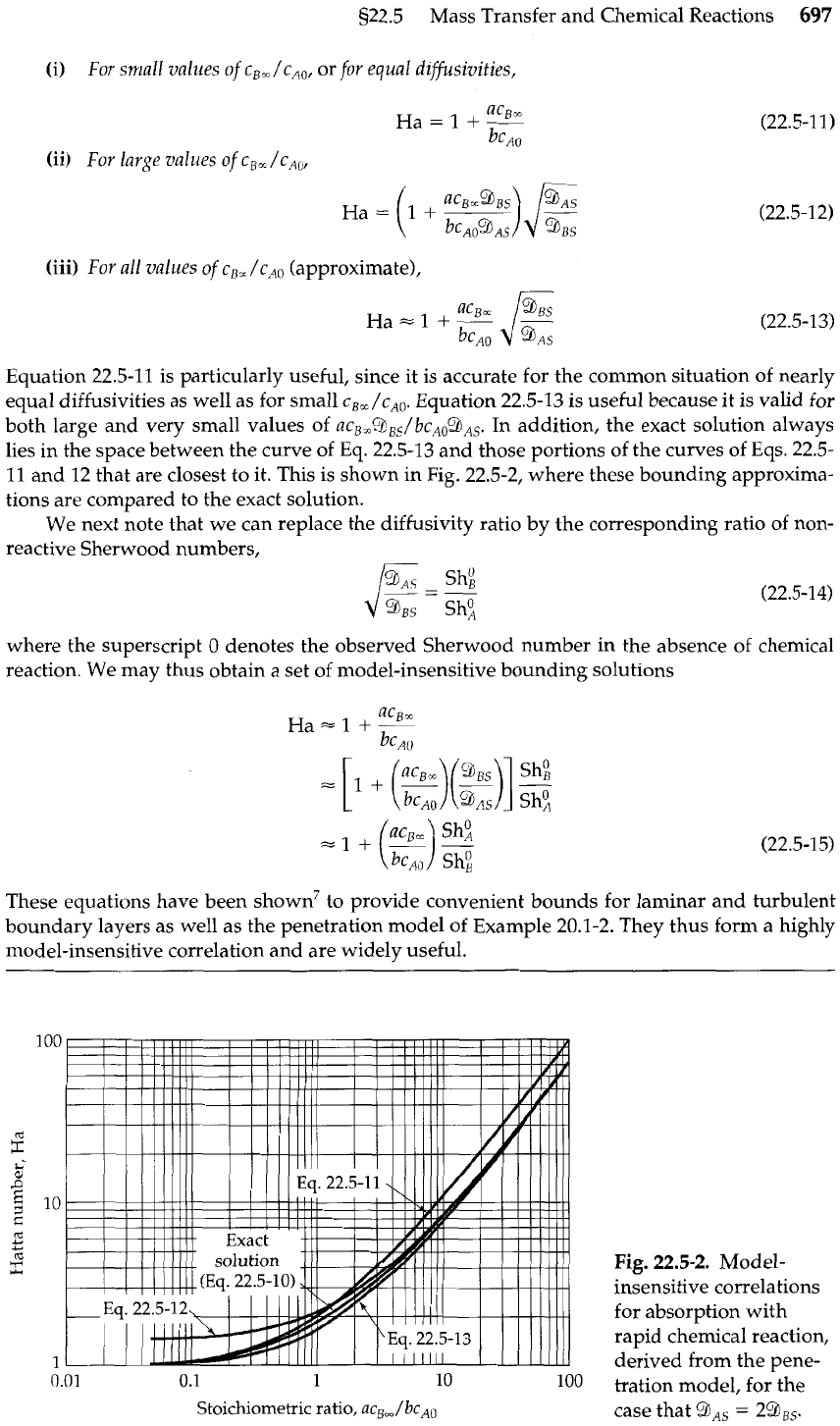
Equation 22.5-11 is particularly useful, since it is accurate for the common situation of nearly

equal diffusivities as well as for small cBm /cAO. Equation 22.5-13

useful because it is valid for

both large and very small values of a~,,~,~/bc~~~,,. In addition, the exact solution always

lies in the space between the curve of Eq. 22.5-13 and those portions of the curves of Eqs. 22.5-

11 and 12 that are closest to it. This is shown in Fig. 22.5-2, where these bounding approxima-

tions are compared to the exact solution.

We next note that we can replace the diffusivity ratio by the corresponding ratio of non-

reactive Sherwood numbers,

where the superscript

denotes the observed Sherwood number in the absence of chemical

reaction. We may thus obtain a set of model-insensitive bounding solutions

These equations have been shown7 to provide convenient bounds for laminar and turbulent

boundary layers as well as the penetration model of Example 20.1-2. They thus form a highly

model-insensitive correlation and are widely useful.

Fig.

22.5-2.

Model-

insensitive correlations

for absorption with

rapid chemical reaction,

derived from the pene-

0.01

0.1 1 10 100

tration model, foithe

Stoichiometric

ratio,

acB,/bcAo

case that

BAS

29IBs.

698

Chapter

Interphase Transport in Nonisothermal Mixtures

522.6

COMBINED HEAT AND MASS TRANSFER

FREE CONVECTION

In this section we consider briefly some important interactions among the transfer

processes, with emphasis on free convection. This is an extension of our earlier discus-

sion of free-convection heat transfer in 514.6 and is reasonably well understood.

Combined heat and mass transfer by free convection is among the simple examples

of interaction between all three transport phenomena. The dimensionless equations de-

scribing them have been given in Eqs.

19.5-8

ll.

Numerical integration of these equa-

tions is possible,' but we can obtain simple, useful results via boundary layer theory. We

consider two particularly simple problems in the examples that follow.

Develop an expression for the combined free-convection heat and mass transfer for the spe-

cial case of equal Prandtl and Schmidt numbers. Assume that transfer is between a surface of

of Grashof

constant temperature and composition, and a large uniform surrounding fluid.

Numbers

SOLUTION

This is a direct extension of the boundary conditions of Example 11.4-5. Then if the dimen-

sionless temperature and composition are defined analogously, it follows that

every-

where within the system under investigation.

It then follows that the solution of this mixed convection problem is identical to that for

heat or mass transfer alone, but with Gr or Gr, replaced by the sum (Gr

Gr,). This simplifi-

cation is widely used for the air-water system, where the small difference between the Sc and

Pr numbers does not have a significant effect.

Thus for evaporation from a water-wetted vertical plate (with Sc

0.61 and Pr

0.73),

one may use Eq. 11.4-11 with

0.518 to obtain

Nu,

0.518[0.73(Gr

~r,)]'/~

Sh,

0.518[0.61(Gr

~r,)]'/~

Note that the i-th powers of Pr and Sc are 0.92 and 0.88, respectively. This difference is

hardly significant in view of the uncertainties of any actual situation and the boundary layer

model on which these results are based. Note also that the thermal Grashof number is nor-

mally by far the larger, so that neglect of this interaction would greatly underestimate the

evaporation rates.

There are many situations-for example, the evaporation of solvents with low volatility-

where thermal Grashof numbers are much larger than their mass transfer counterparts (Gr

Free-Convecti0n

Heat

Gr,) and the Schmidt numbers exceed the Prandtl numbers (Sc

Pr). Under these conditions,

Transfer as a Source of

the thermal buoyant forces provide a momentum source, which in turn provides a convective

Forced-Convection

flow to drive mass transfer. It has been shown2 that the thermally induced gradient of up-

Mass Transfer

ward velocity at the surface of a vertical flat plate of length

is given by

Here

is the distance measured upward along the plate,

is measured outward into the fluid,

and

is the difference between the plate temperature and the temperature of the surround-

ings. This is an asymptotic expression for large Prandtl number, but is also useful for gases.

Develop expressions for the local and mean Sherwood numbers.

Wilcox,

Chem.

Eng.

Sci.,

13,113-119

(1961).

Acrivos,

Pkys.

Fluids,

3,657-658

(1960).

522.7 Effects of Interfacial Forces on Heat and Mass Transfer

699

SOLUTION

The thermal free convection provides a velocity field within which the mass transfer bound-

ary layer develops. Given this velocity field, we may use the mass transfer analog of Eqs.

12.4-30 and 29 along with the definition NuIoc

D/I'($)&

to obtain a description of the mass

transfer rate in two-dimensional flow:

Here

is the dimensionless velocity gradient at the wall

(I,

and

are arbitrary reference quantities

used in the definition of the Reynolds number). For free convection it is convenient to use the

plate height

for

and

v/L

for

v,.

Then the Reynolds number is unity, and the quantity

(L2/v)(dv,/dy)ly,,. Then Eq. 22.6-4 becomes

The mean Sherwood number, obtained by averaging over the plate surface, is

Sh,

0.79(GrS~)"~

Note that these last two equations show features of both free and forced convection

lami-

nar boundary layers: the $-power of the Grashof number for

free

convection and the $power

of the Schmidt number for forced convection.

Moreover,

can now test the effect of Sc/Pr, because we know from the preceding ex-

ample and Table 14.6-1 that, for Pr

Sc,

Sh,

0.67(GrS~)'/~ (22.6-8)

in which the coefficient is lower than that in

Eq.

22.6-7 by the ratio 0.85. The Sherwood num-

ber Sh, will lie between the predictions of Eqs. 22.6-7 and 8 for Sc

Pr and Pr

Arguments similar to those used in

Eq.

14.6-6 now suggest the following extension of

Eqs. 22.67 and 68,

Sh,

0.73(1

0.1)

(G~SC)'/~(SC/P~)"'*

(0.492/~r)~/'~]~'~

for Sc

Pr and Pr

0.73. This result is correct for the limits Pr

0.73 and Pr

and hence

can include the evaporation of solvents in air. This analysis can also be extended to other

shapes.

522.7

EFFECTS OF INTERFACIAL FORCES

ON HEAT AND MASS TRANSFER

this section we consider briefly some important interactions among the three transfer

processes, with emphasis on the effects of variable interfacial tension

(Marangoni

effects).

The importance of this subject stems from the prevalence of direct fluid-fluid contact in

mass transfer systems, but it can also be important in similar heat transfer operations.

Still poorly understood diffusional processes permit violation of the no-slip condition on

700

Chapter

Interphase Transport in Nonisothermal Mixtures

fluid flow over solid surfaces in the neighborhood of advancing menisci.' As for the dis-

torting effects of surface tension gradients on mass and heat transfer in gas-liquid con-

tacting, these will enter through a description of the boundary conditions.

According to

Eq.

llC.6-4, if the stresses in the gas (phase

11)

are ignored, the interfa-

cial tangential stresses acting on an interface with normal unit vector

are given bf

[(6

nn)

711

-VSa

(22.7-1)

where

is the surface tension V9s the two-dimensional gradient operator in the inter-

face, and

nn)

is a "projection operator" that selects those components of

that

lie in the interfacial tangent plane. For example, if

is taken to be the unit vector in the

direction, Eq. 22.7-1 gives

which are the interfacial tension forces in the

and

directions acting in the xy-plane.

The surface-tension-induced stresses are typically of the same order as their hydro-

dynamic counterparts, and the flow phenomena that may result from them are known

collectively as

Marangoni

effect^.^

has been shown4 that mass transfer rates can be

in-

creased up to threefold by Marangoni effects, but can also be reduced in other circum-

stances.

The nature and extent of Marangoni effects depend strongly on the system geometry

and the transport properties, and it will be convenient to consider here four specific

examples:

(i)

drops and bubbles surrounded by

liquid continuum

(ii)

sprays of drops in a gaseous continuum

(iii)

supported liquid films in a gaseous or liquid continuum

(iv)

foams of gas bubbles in a liquid continuum

These systems, each important in practice, show very different behavior from one an-

other.

For drops and bubbles moving through a liquid continuum, the primary problems

are surfactants or microscopic particles that can reduce or eliminate the "Hadamard-

Rybczinski circulation" and also hinder the periodic mixing accompanying oscillation in

Ludviksson and

Lightfoot,

AlCkE

Journal,

14,674-677 (1968);

Thompson and

S. M. Troian,

Phys.

Rev.

Letters,

63,766-769 (1997);

Marmur, in

Modern Approach to Wettability: Theory

and Applications

(M.

Schrader and

Loeb, eds.), Plenum Press (1992);

Schaeffer and P.-Z. Wong,

Phys. Rev. Letters,

80,3069-3072 (1998).

In Eq. 3.2-6 of

Edwards,

Brenner, and

Wasan,

Interfacial Transport Processes and

Rheology,

Butterworth-Heinemann, Boston (1991), the operator

nn)

is called the "dyadic surface

idemfactor"; the same quantity is called the "projection tensor" by

Slattery,

Interfacial Transport

Phenomena,

Springer Verlag, New York (1990),

1086. Both books contain a wealth of information on

surface tension, surface viscosity, surface viscoelasticity, and other properties of interfaces and their

methods of measurement.

M. Marangoni,

Tipographia deifrntelli Fusi,

Pavia (1865);

Ann. Phys.

(Poggendorf), 143,337-354

(1871). Historical articles on the Marangoni effects are

Scriven and

Sternling,

Nature,

187,

186-188 (1960), and S. Ross and P. Becher,

Coll. Interfac. Sci.,

149,575-579 (1992).

good overview of Marangoni effects and related phenomena, with emphasis on liquid-liquid

systems, is provided in

Godfrey and M.

Slater,

Liquid-Liquid Extraction Equipment,

Wiley, New

York (1994), pp. 68-75.

theory offered by

Sternling and

Scriven,

AlChE Journal,

5,514-523

(1959), provides useful insight but is considered too simple to give reliable predictions of the onset of

instabilities.

s22.7 Effects of Interfacial Forces on Heat and Mass Transfer

701

larger drops or

bubble^.^

These are discussed briefly in Example 22.3-4. These situations

are important in gas absorbers and liquid extractors. For sprays of drops in a gas, impor-

tant

large distillation columns, Marangoni forces play no significant role.6

Foam beds, important in smaller distillation columns, and supported films, impor-

tant in a wide variety of packed columns, are particularly interesting. Both are strongly

affected by surface-tension gradients resulting from the changes of surface tension with

composition of the adjoining streams.

Foam beds are stabilized when the buik liquid has a lower surface tension than that in

equilibrium with the bulk gas, called a "positive system." In such a situation, interfacial

tension tends to be higher where bubbles are close together than where they are far apart,

and the shrinking of high-surface-tension regions tends to drive the bubbles apart, thus

stabilizing the foam. Where there are only small differences in surface tension, or where

the direction is reversed, a "negative system," there is no stabilizing effect and the foaming

is poor. Concentration of ethanol from water is interesting, because it has strong positive

surface tension gradients where the relative volatility is high, but becomes very nearly

neutral as the azeotrope is approached. Thus, for a bubble-cap column, stage efficiencies

are high where least needed and low as the azeotropic composition is approached.

In packed columns, where the descending liquid is supported on solid surfaces as

thin films, the situation is quite different. Here the surface tension of the descending liq-

uid decreases downward for a positive system and is subject to hydrodynamic instabil-

ity to form narrow rivulets. These markedly decrease interfacial area and mass transfer

effectiveness. In negative systems, on the other hand, films are stabilized, and mass

transfer is more effective than for neutral systems. No quantitative analysis of this situa-

tion appears to be available, but it has been shown that instabilities found by Zuiderweg

and Harmens for wetted-wall columns can be predicted by linearized stability analy~is.~

Stability analysis also suggests that the presence of a positive surface-tension gradient

should improve the efficiency of condensers. Another study of stability for very small

films opens up new possibilities for microfluidic processors.8

EXAMPLE

22.7-1

Elimination of

The presence

surfactants can stop Hadamard-Rybczinski circulation in a rising gas bubble.

Explain this phenomenon (see Fig. 22.7-1).

Circulation in a

SOLUTION

Rising

Gas

Circulation results in stretching of the surface at the top of

rising bubble and shrinking of

the surface at the bottom. As

result, surfactant accumulates at the bottom, producing a

higher than average concentration there, whereas a lower-than-average concentration exists

at the top. Since surfactants reduce surface tension, this results in a surface-tension-induced

stress (in spherical coordinates)

tending to oppose the interfacial deformation (see

Eq.

22.7-1). If the magnitude of this stress

reaches the value that would occur on a rising solid sphere (see

Eq.

2.6-6)

w'm

rrol

r=R

sin

circulation will stop.

Angelo and

Lightfoot,

AICkE Journal,

12,751-760 (1966).

Zuiderweg and A. Harmens,

Chem. Eng.

Sci.,

9,89-103 (1958).

Wang,

Ludviksson, and

Lightfoot,

AIChE Journal,

17,1402-1408 (1971).

Kataoka and

Troian,

Nature,

402,794-797 (16

December

1999).

702

Chapter 22 Interphase Transport in Nonisothermal Mixtures

Surfactant

adsorption

Surfactant

release

Fig.

22.7-.1

Surfactant transport during Hadamard-

Rybuynski circulation

As a practical matter, even small amounts of surfactant prevent circulation. Small con-

centration of microscopic suspended particulates have a similar effect, being swept to the rear

of bubbles and forming a rigid surface.

Among the simplest mass-transfer-induced Marangoni effects is instability

a falling film re-

sulting from counterflow adsorption of vapors with a high heat of solution. An important

Marangoni Instability

representative example is the counterflow absorption of

HCI

vapor into water, which is so in-

in a Falling Film

efficient that cocurrent flow is preferable. Explain this effect.

UTION

This situation can be simulated by allowing a film of water to flow down a plate that is colder

at the top than at the bottom. If sufficient care is taken, one can obtain a sinusoidally varying

film thickness, as shown9 by interferometry in Fig. 22.7-2(a). Here each new dark line repre-

sents a line of constant thickness, differing from its neighbors by one-half wavelength of light

in the water.

This situation corresponds to a series of parallel

roll

cells

of the type pictured in Fig. 22.7-

2(b),

driven by lateral surface tension gradients. These gradients, in turn, result from small

variations in film thickness caused by inevitable small spatial variations of surface velocity:

the thicker regions move faster and thus tend to be colder than the thin regions. A simple per-

turbation analysis1 shows that perturbations of some widths grow faster than others, and the

fastest growing ones tend to dominate. The periods of the sinusoidal lines in Fig. 22.7-2(a)

correspond to these fastest growing disturbances.

Such regularity is, however, seldom observed in practice. More commonly one sees occa-

sional thick rivulets surrounded by large thin regions. These thin regions, taking up most of

the available surface, are both slowly moving and quickly saturated and are thus ineffective

for mass transfer. Only the rivulets are effective, and their total surface area is very small.

Similar behavior is observed for surface-tension gradients caused by vertical variations in

composition. However, in that case the behavior is more complicated and requires an analy-

sis of interphase mass tran~fer.~

522.8 Transfer Coefficients at High Net Mass Transfer Rates

703

Fig.

22.7-2.

(a) Initiation of Marangoni instability

in a draining liquid fluid film.

(b)

Fully developed

Marangoni instability.

(c)

Qualitative picture of

vertical roll-cell disturbances

[V.

Ludviksson and

Lightfoot,

AIChE

Journal, 14,620-626 (1968)l.

522.8

TRANSFER COEFFICIENTS AT

HIGH

NET MASS TRANSFER RATES

High net mass transfer rates across phase boundaries distort the boundary-layer profiles

of velocity and temperature as well as species concentration, and they also alter the

boundary layer thicknesses. Both of these effects tend to increase friction factors and the

heat and mass transfer coefficients, if the mass transfer is toward the boundary, and to

reduce them in the reverse situation. These usual trends are reversed, however, in free

convection and in flows driven by a rotating surface. The magnitudes of such changes

are dependent on the system geometry, boundary conditions, and the magnitudes of the

governing parameters such as the Reynolds, Prandtl, and Schmidt numbers, and they

are accompanied by the effects of changes in physical properties. They can also either in-

crease or decrease the hydrodynamic stability. Accurate allowance for the effects of net

mass transfer thus requires extensive calculation and/or experimentation, but some of

the more salient features can be illustrated by using idealized physical models, and this

is the approach we follow here.

We begin with the classic stagnant-film model, which provides simple estimates of the

profile distortion, but is incapable of predicting changes in the effective film thickness.

We then discuss the perzetratiorz model and the flat-plate laminar boundary layer model. We

conclude with several illustrative examples, the last of which is a complete numerical ex-

704

Chapter

Interphase Transport in Nonisothermal Mixtures

ample of boundary layers on

spinning disk. This example will provide a useful ap-

praisal of model sensitivity.

As pointed out in 922.1, when high net mass transfer rates are being considered, we

introduce a modified notation for the transfer coefficients:

The black dots in

k;,,,,

and

hioc

imply that the distortions of the concentration and temper-

ature profiles resulting from high net mass transfer rates are being included.

The relations between these transfer coefficients and those defined in Eqs. 22.1-7 and 8

are

lim

&,,oc

4'10c

NAo+NB,,-+O

(22.8-2a)

This shows explicitly the limiting process that relates the two types of transfer coefficients.

The

Stagnant-Film

have already discussed this model briefly in 518.2 and more fully in Example 19.4-1.

combining the expressions in Eqs. 19.4-16 and 17 with the definitions in Eqs. 22.8-la

and lb, we get for the system in Fig. 22.8-1

Interface

Velocity Temperature Concentration

profile profile profile

Fig.

22.8-1.

Steady flow along a flat surface with rapid mass trans-

fer into the stream. The unbroken curves represent the true pro-

files, and the broken curves are predicted by the film model.

Lewis

and

C. Chang,

Trans.

AIChE,

21,127-136 (1928).

Ackerman,

Forschungsheft,

382,l-16 (1937).

Colburn and

Drew,

Trans.

AIChE,

33,197-212 (1937).

Mickley, R. C. Ross,

Squyers, and

Stewart,

NACA

Tech. Note

3208

(1954).

s22.8 Transfer Coefficients at High Net Mass Transfer Rates

705

By following the limiting processes indicated in Eqs. 22.8-2a and 2b, we then get expres-

sions for the transfer coefficients in the low net mass transfer limit:

These limiting values are found by expanding the right sides of Eqs. 22.8-3 and 4 in Tay-

lor series and retaining two terms. Substitution of Eqs. 22.7-5 and 6 into Eqs. 19.4-16 and

enables us to eliminate the film thicknesses (which are ill-defined) in favor of the

transfer coefficients at low mass-transfer rates (which are measurable):

These equations are the principal results of the film model. They show how the conduc-

tive energy flux and the diffusion flux at the wall depend on

NAo

and

NBo.

In this model,

the effects of net mass transfer on the conductive and diffusive interfacial fluxes are

clearly analogous. Although these relations were derived for laminar flow and constant

physical properties, they are also useful for turbulent flow and for variable physical

properties (see Problem 22B.3).

The results for heat and mass transfer can be summarized in two equations:

Equation 22.8-9 gives the correction factors

and

by which the coefficients

kX,,,,

and

bloc

must be multiplied to obtain the coefficients at high net mass transfer rates. Equation

22.8-10 gives the concentration and temperature profiles. The meanings of the symbols

are summarized in Table 22.8-1.

Table

22.8-1

Summary of Dimensionless Quantities to be Used for

All

Models Discussed in 522.8. Mass-based versions appear in 520.2 and

s22.9.

correction factors

flux ratios

rate factors

profiles

dimensionless distance from wall

Mass transfer Heat transfer

706

Chapter

Interphase Transport in Nonisothermal Mixtures

Fig.

22.8-2.

The variation of the transfer

coefficients with mass transfer rate, as

given

the

film

model (see

Eq.

22.8-9).

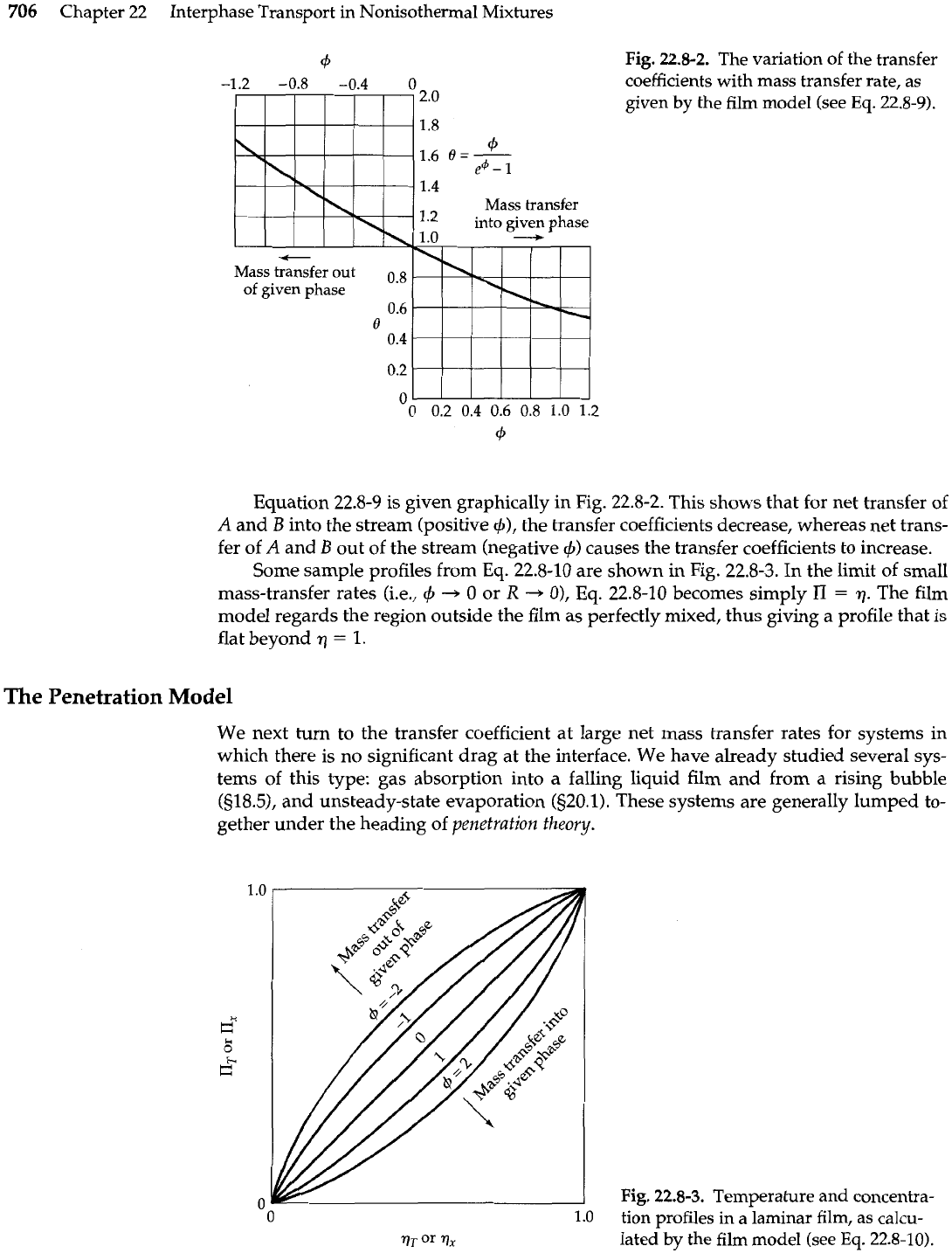
Equation 22.8-9 is given graphically in Fig. 22.8-2. This shows that for net transfer of

and

into the stream (positive

+),

the transfer coefficients decrease, whereas net trans-

fer of

and

out of the stream (negative

causes the transfer coefficients to increase.

Some sample profiles from

Eq.

22.8-10 are shown in Fig. 22.8-3. In the limit of small

mass-transfer rates (i.e.,

O),

Eq.

22.8-10 becomes simply

The film

model regards the region outside the film as perfectly mixed, thus giving a profile that is

flat beyond

The Penetration Model

We next turn to the transfer coefficient at large net mass transfer rates for systems in

which there is no significant drag at the interface. We have already studied several sys-

tems of this type: gas absorption into a falling liquid film and from a rising bubble

(§18.5), and unsteady-state evaporation (520.1). These systems are generally lumped to-

gether under the heading of

penetration theory.

Fig.

22.8-3.

Temperature and concentra-

1.0

tion profiles in a laminar film, as

calcu-

lated

the film model (see

Eq.

22.8-10).