Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.


30 2 Models of Dynamics
for K(t −s), if the couplings γ
i
and the frequencies ω
i
are such that g
i
γ
i
ω
2
i
(where
g
i
is the weight factor) is independent of i, in that case,
K(t −s) =
i
γ
2
i
ω
2
i
cosω
i
(t −s)
= lim
ω
max
→∞
ω
max
−ω
max
γ
2
ω
2
P (ω)cosω(t −s)dω
= lim
ω
max
→∞
ω
max
0
cosω(t −s)dω (using P(ω)=
ω
2
2γ
2
)
= lim
ω
max
→∞
sinω
max
(t −s)
t −s
= δ(t −s) (2.2.13)
In this limit, the noise at time t is not correlated with the noise at a different time
s. Such a noise is called a Markovian or a white noise. Using the δ-function form
of K(t −s), we now have the Langevin equation in the form
˙
p(t) =−p(t ) +f(t) (2.2.14)
where
f(t)f(s)=K
B
TK(t−s) (2.2.15)
It is worth noting that the appearance of in the relaxation term in Eq.(2.2.14)
and the correlation function in Eq.(2.2.15) is not accidental and is related to the
existence of an equilibrium distribution.
We now turn to Eq.(2.2.14) and discuss the solution. As is to be expected, the
solution for p(t) is stochastic and hence only quantities which are sensible are the
various moments of p(t). The solution of Eq.(2.2.14) is straightforward to write
down and we have
p(t) =e
−t
t
0
e
s
f(s)ds+p(0)e
−t
(2.2.16)
Clearly, p(t)=p(0)e
−t
. For the second moment
p(t
1
)p(t
2
)=e
−(t
1
+t
2
)
t
1
0
e
s
1
f(s
1
)ds
1
t
2
0
e
s
2
f(s
1
)ds
2
+p
2
(0)e
−(t
1
+t
2
)
= e
−(t
1
+t
2
)
×K
B
T
t
1
0
e
2s
1
ds
1
+p
2
(0)e
−(t
1
+t
2
)
(t
2
>t
1
)
= e
−(t
1
+t
2
)
K
B
T
2
(e
2t
1
−1) +p
2
(0)e
−(t
1
+t
2
)
=
K
B
T
2
e
−(t
2
−t
1
)
+
p
2
(0)−
K
B
T
2
e
−(t
1
+t
2
)
(2.2.17)
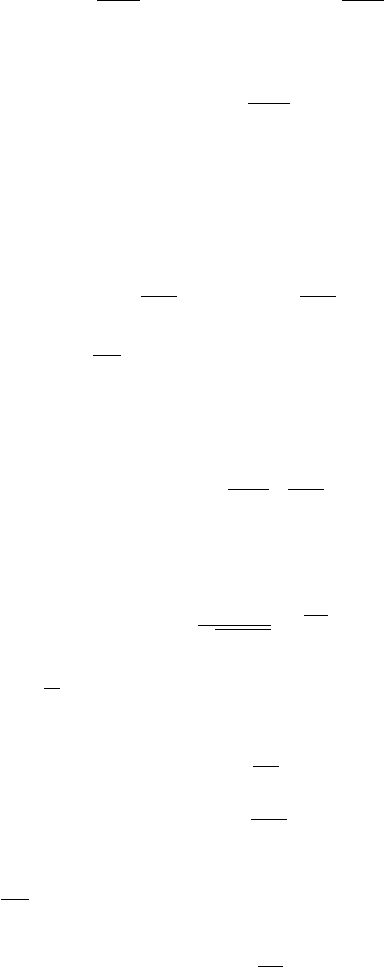
2.2 Langevin Picture 31
Considering the case t
1
>t
2
, we have in general
p(t
1
)p(t
2
)=
K
B
T
2
e
−|t
1
−t
2
|
+
p
2
(0)−
K
B
T
2
e
−(t
1
+t
2
)
.
If the initial distribution is such that
p
2
(0)=
K
B
T
2
,
then the fluctuation correlations decay as
p(t
1
)p(t
2
)=p
2
(0)e
−|t
1
−t
2
|
.
For equal time correlation on the other hand
p
2
(t)=
k
B
T
2
+
p
2
(0)−
k
B
T
2
e
−2t
.
As t →∞, p
2
(t)→
k
B
T
2
. We can construct the n
th
order correlation function
from the solution written down in Eq.(2.2.16) in a straightforward manner and one
finds for t →∞,
p
2n+1
(t)=0
p
2n
(t)=
(2n)!
n!2
n
k
B
T
2
n
(2.2.18)
With all the correlation functions known we can write down what the distribution
is for t →∞. The moments of Eq.(2.2.18) indicate a Gaussian distribution with,
P(p)=
1
√
πK
B
T
e
−
p
2
k
B
T
(2.2.19)
Writing F(p)=
p
2
2
as a kind of energy expression, we can write the Langevin
equation that we started out with as
˙p =−
∂F
∂p
+ f
f(t)f(s)=2
k
B
T
2
δ(t −s)
= 2 D δ(t−s) (2.2.20)
where D =
k
B
T
2
. With the Langevin equation appearing in the form of Eq.(2.2.20),
one is guaranteed the existence of an equilibrium distribution given by
P(p)∝e
−
f(p)
D
.

32 2 Models of Dynamics
In our specific example F(p) was a quadratic function of p. As we will show in
the next section, this restriction is not necessary. Any Langevin equation with the
structure
˙p =−
∂F
∂p
+f
f(t)f(s)=2 D δ(t−s) (2.2.21)
has the equilibrium distribution e
−
F
D
.
To end this section, we ask what is the probability distribution associated with
the noise f(t). It is a straightforward matter to carry out the calculation of the
higher moments since all the moments of the initial values q
i
(0) and p
i
(0) are
known. One finds,
f(t
1
)f (t
2
).....f (t
2n+1
)=0
while f(t
1
)f (t
2
).....f (t
2n+1
)=(2D)
n
{δ(t
1
−t
2
)δ(t
3
−t
4
)
.....δ(t
2n−1
−t
2n
) +all permutations
of the time intervals}
(2.2.22)
Given the above correlation functions, the probability of f(t)being a given function
f(t)is
P [f ]=N exp
−
1
4 D
∞
−∞
|f(s)|
2
ds
where the normalization is given by the functional integral
N
−1
=
D[f ]exp
−
1
4D
∞
−∞
|f(s)|
2
ds
.
It will be an useful exercise for the reader to verify that the above distribution does
lead to the correlation function in Eq.(2.2.22).
2.3 Fokker Planck Description
In this section, we discuss a different kind of equation of motion - an equation of
motion for the probability P itself.The question is what is the probability P(p(t),t)
of the variable p acquiring the value p(t) at time t? The equation of motion for
the variable p is that given in Eq.(2.2.21). It is easiest to proceed by considering
time as a discrete variable and taking a sequence t
0
,t
1
,t
2
.......t
n
,t
n+1
, ..... such

2.3 Fokker Planck Description 33
that t
n+1
−t
n
=δt is an infinitesimal. Writing p(t
n
) =p
n
, the discretized form of
Eq.(2.2.21) is
p
n+1
=p
n
−g (2.3.1)
where g =
∂F
∂p
δt −
¯
f(t)(δt)
1/2
(2.3.2)
with the definition
¯
f(t)=f (t)(δt)
1/2
(2.3.3)
so that the correlation function of
¯
f(t)is
¯
f(t)
¯
f(t
)=2Dδ
tt
(2.3.4)
δ
tt
being the Kronecker delta. Our aim is to go from P(p,t) to P(p(t +δt), t +
δt), i.e. the probability of finding the value p(t +δt) of the variable p at time
t +δt. In terms of the discretized time variable, we need to go from P(p
n
,t
n
) to
P(p
n+1
,t
n+1
). Obviously, this is achieved by using the equation of motion i.e.
P(p
n+1
,t
n+1
) =
P(p
n
,t
n
)δ(p
n+1
−p
n
+g) dp
n
(2.3.5)
The averaging has to be done over all possible realizations of the noise f(t) that
occurs in g i.e.
.......=N
D[f ](.......) exp
−
1
4 D
∞
−∞
|f(s)|
2
ds
(2.3.6)
We now make use of the fact that g is small (O(δt)
1/2
) and expand the δ-function
as
δ(p
n+1
−p
n
+g) = δ(p
n+1
−p
n
) +g
∂
∂p
n
δ(p
n+1
−p
n
)
+
g
2
2
∂
2
∂p
2
n
δ(p
n+1
−p
n
) +......... (2.3.7)
Inserting this expansion in Eq.(2.3.5), we note the following
P(p
n
,t
n
)δ(p
n+1
−p
n
)dp
n
=P(p
n+1
,t
n
) (2.3.8)
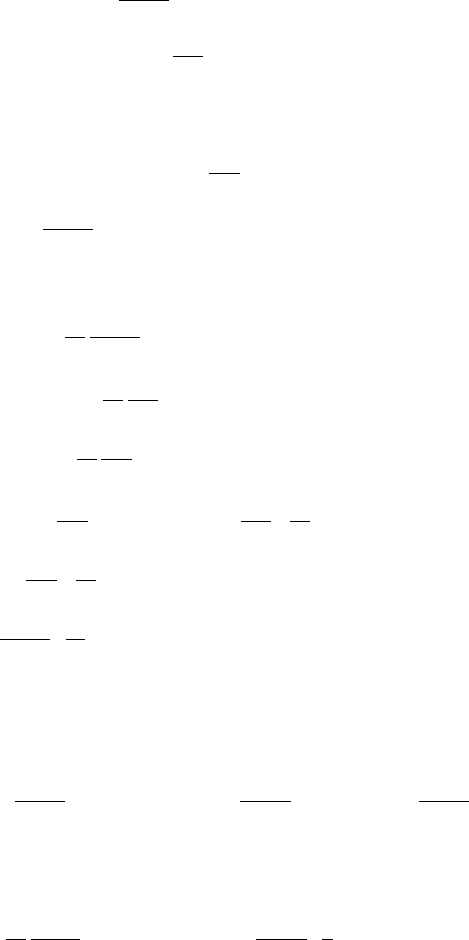
34 2 Models of Dynamics
P(p
n
,t
n
)g
∂
∂p
n+1
δ(p
n+1
−p
n
)dp
n
=−
P(p
n
,t
n
)g
∂
∂p
n
δ(p
n+1
−p
n
)dp
n
=
−P(p
n
,t
n
)gδ(p
n+1
−p
n
)
p
n
=∞
p
n
=−∞
+
δ(p
n+1
−p
n
)
∂
∂p
n
gP(p
n
,t
n
)
dp
n
=
∂
∂p
n+1
gP(p
n+1
,t
n
)
(2.3.9)
and
P(p
n
,t
n
)
g
2
2
∂
2
∂p
2
n+1
δ(p
(
n +1) −p
n
)dp
n
=
P(p
n
,t
n
)
g
2
2
∂
2
∂p
2
n
δ(p
n+1
−p
n
)
=
P(p
n
,t
n
)
g
2
2
∂
∂p
n
δ(p
n+1
−p
n
)
p
n
=∞
p
n
=−∞
−
∂
∂p
n
[δ(p
n+1
−p
n
)]×
∂
∂p
n
g
2
2
P(p
n
,t
n
)
dp
n
=
∂
2
∂p
2
n
g
2
2
P(p
n
,t
n
)
δ(p
n+1
−p
n
)dp
n
=
∂
2
∂p
2
n+1
g
2
2
P(p
n+1
,t
n
)
(2.3.10)
In the above derivations, we have always assumed that P(p
n
) →0asp
n
becomes
large. Inserting the expression for g from Eq.(2.3.2) in Eq.(2.3.9), we find on
implementing the average that
P(p
n
,t
n
)g
∂
∂p
n+1
δ(p
n+1
−p
n
)dp
n
=
d
dp
n+1
P(p
n+1
,t
n
)
∂F
∂p
n+1
δt
(2.3.11)
Doing the same in Eq.(2.3.10) and retaining the terms only up to O(δt),wehave
P(p
n
,t
n
)
g
2
2
∂
2
∂p
2
n+1
δ(p
n+1
−p
n
)dp
n
=
d
2
dp
2
n+1
1
2
2DP (p
n+1
,t
n
)
δt
(2.3.12)

2.3 Fokker Planck Description 35
Making use of Eqns.(2.3.8), (2.3.11) and (2.3.12) the evolution of Eq.(2.3.5) reads
P(p
n+1
,t
n+1
) = P(p
n+1
,t
n
) +
d
dp
n+1
P(p
n+1
,t
n
)
∂F
∂p
n+1
δt
+
d
2
dp
2
n+1
DP(p
n+1
,t
n
)
δt (2.3.13)
Absorbing the to simplify redefine the time scale, the differential equation for
P(p,t) reads,
∂P (p, t)
∂t
=
∂
∂p
∂F
∂p
P
+D
∂
2
∂p
2
P (2.3.14)
This is the Fokker-Planck equation that corresponds to the Langevin equation
of Eq.(2.2.21). What about the equilibrium distribution P
eq
? This is obtained by
setting
∂
∂t
P
eq
=0
and immediately leads to
P
eq
∼e
−F/D
(2.3.15)
This establishes what we mentioned at the end of the last section. The Langevin
equation given in Eq.(2.2.21) has associated with it an equilibrium distribution.
We have thus far discussed Langevin and Fokker-Planck equations for a single
variable. As discussed in the introduction, mesoscopic systems which will be our
concern are described by fields φ(r,t) rather than a single variable. Instead of a
function F of a single variable for the equilibrium distribution, as we had before,
we would have to consider a functional F(φ(r,t)). If we are discussing critical
phenomena, this functional would be the Ginzburg-Landau free energy functional
(for a scalar field φ)
F(φ(r,t))=
d
D
r
m
2
2
φ
2
+
1
2
(∇φ)
2
+
λ
4
φ
4
(2.3.16)
In the above λ is a coupling constant and
m
2
∝(T −T
c
),
where T
c
is the critical temperature. The Langevin equation corresponding to
Eq.(2.2.21) is now given by
∂φ
∂t
=−
δF
δφ
+N
N(r
1
,t
1
)N(r
2
,t
2
)=2Dδ(t
1
−t
2
)δ(r
2
−r
2
) (2.3.17)
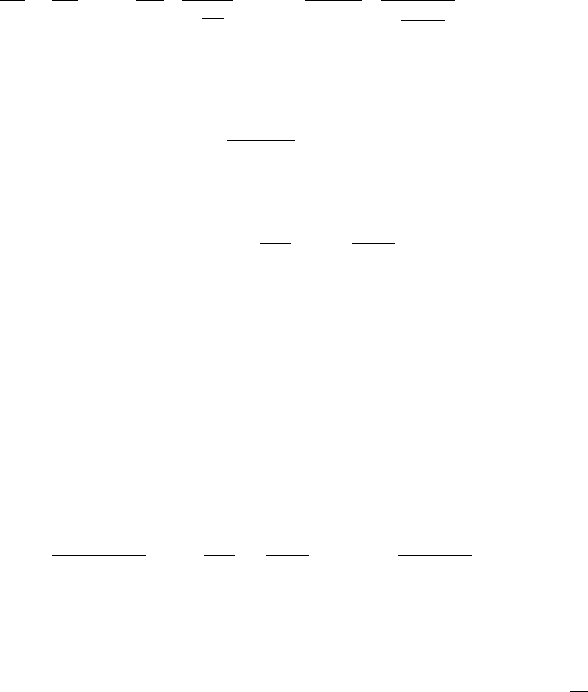
36 2 Models of Dynamics
Notice that instead of the ordinary derivative, we have a functional derivative in
Eq.(2.3.17), the Markovian property extends to space as well - the noise is not
correlated in time or space. For completeness, we provide the definition of the
functional derivative as
δF
δφ
=
∂F
∂φ
−
i
∂
∂x
i
∂F
∂(
∂φ
∂x
i
)
+
i,j
∂
2
∂x
i
∂x
j
∂F
∂(
∂
2
φ
∂x
i
∂x
j
)
+...... (2.3.18)
Instead of working with the field φ(r,t), we can work with its Fourier components
φ
k
(t)
φ(r,t)=
1
(2π)
D/2
d
D
ke
i
k.r
φ
k
(t) (2.3.19)
The Langevin equation for φ
k
(t) now reads
∂φ
k
∂t
=−
∂F
∂φ
−
k
+N
k
with N
k
1
(t
1
)N
k
2
(t
2
)=2Dδ(
k
1
+
k
2
)δ(t
1
−t
2
) (2.3.20)
Associated with the Langevin equations of Eq.(2.3.17) or Eq.(2.3.20) is the proba-
bility distribution e
−F/D
. We now ask what is the associated Fokker-Planck equa-
tion. This is easiest to answer when the Langevin equations are cast in the form of
Eq.(2.3.20). Instead of a single variable Langevin equation, we now have Langevin
equations for an infinite number of variables φ
k
. The Fokker-Planck equation is
that for P({φ
k
},t), where P is the probability of each of the variables φ
k
acquiring
the value φ
k
at time t. The derivation of the evolution equation parallels the one
we have given already and the final result is
∂P({φ
k
},t)
∂t
=
k
∂
∂φ
k
P
∂F
∂φ
−
k
+D
k
∂
2
P
∂φ
k
∂φ
−
k
(2.3.21)
As expected, this Fokker-Planck equation does support the equilibrium distribution
e
−F/D
.
We can write down Langevin equations for fields which cannot be cast in the
form of Eq.(2.3.17), i.e. the drive on the R.H.S does not have the structure
δF
δφ
.In
this case the existence of an equilibrium state is not assured. A non-equilibrium
steady state can, however, exist.
2.4 Dynamics of a Magnet near Its Critical Point
In this section we will be setting up the equation of motion that is appropriate for
describing the dynamics of a Heisenberg ferromagnet. At first, we look at the stat-
ics. The order parameter for the transition is the three dimensional magnetization

2.4 Dynamics of a Magnet near Its Critical Point 37
vector φ(r,t) with the components φ
1
,φ
2
and φ
3
and the free energy functional
determining the probability distribution is
F =
d
D
r
m
2
2
φ
i
φ
i
+
1
2
(
∇φ
i
).(
∇φ
i
) +
λ
4
(φ
i
φ
i
)
2
(2.4.1)
The Langevin equation is, as recommended in Eq.(2.3.17)
˙
φ
i
=−
δF
δφ
i
+N
i
(2.4.2)
N
i
(r
1
,t
1
)N
j
(r
2
,t
2
)=2(K
B
T)δ
ij
δ(t
1
−t
2
)δ(r
1
−r
2
)
The noise comes from an averaging over very short wavelength fluctuations. The
equations of motion, as written down in Eq.(2.4.2), have a relaxational part and a
stochastic part. We now have to worry about a conservation law associated with the
ferromagnet. If we consider the total magnetization
d
D
rφ, then that has to be
conserved in time. The dynamics as written down in Eq.(2.4.2) does not conserve
the order parameter. For the conserved order parameter,
˙
φ
i
= ∇
2
δF
δφ
i
+N
i
(2.4.3)
and N
i
(r
1
,t
1
)N
j
(r
2
,t
2
)=−2∇
2
(K
B
T)δ
ij
δ(t
1
−t
2
)δ(r
1
−r
2
)
The term ∇
2
acts like the divergence of a current and hence provides the conser-
vation law. For both Eqns.(2.4.2) and (2.4.3), we have the equilibrium distribution
given by e
−F/K
B
T
, the distribution which correctly gives the statics. The relations
between the stochastic and dissipative parts in Eqns.(2.4.2) and (2.4.3) are called
fluctuation dissipation relations (FDR). In dealing with the statics, we will assume
that the static effects have been taken into account already and accordingly the
mass m
2
will be identified with the inverse correlation length and assigned the
correct critical behaviour, i.e.
m
2
=
1
ξ
2
=ξ
−2
0
t
2ν
=ξ
−2
0
T −T
c
T
c
2ν
(2.4.4)
with the exponent ν given by
ν =
1
2
+
1
4
n +2
n +8
+O(
2
) (2.4.5)
where n is the number of components of the order parameter field (n =3 for
our ferromagnet) and =4 −D, where D is the dimensionality of space. The
susceptibility at T =T
c
, will be given by
χ
−1
= k
2−η
(2.4.6)
with η =
1
2
n +2
(n +8)
2
2
+O(
3
) (2.4.7)

38 2 Models of Dynamics
Our Eq.(2.4.2) constitutes what Halperin and Hohenberg describes as the model A
of critical dynamics, while our Eq.(2.4.3) constitutes their model B. These models
comprise a relaxational and a stochastic part. However, physical considerations
dictate another term in the equation of motion. The magnetic moment experiences
a torque due to the local field
h(r) and that causes the magnetization φ
i
to change
as
˙
φ =˜g
φ ×
h (2.4.8)
The local field
h is produced by the local magnetization
φ and we have theexpansion
h =a
1
φ +a
2
∇
2
φ +........ (2.4.9)
Inserting in Eq.(2.4.8)
˙
φ = a
2
˜g
φ ×∇
2
φ
= g
φ ×∇
2
φ (2.4.10)
It should be noted that all other terms in the expansion of Eq.(2.4.9) would give
terms which would be irrelevant for the long wavelength behaviour. In the above
g is a coupling constant.
Knowing that the relaxational part of the equation of motion has to preserve the
total magnetization, we write down the full equation of motion for the ferromagnet
as
˙
φ =g
φ ×∇
2
φ +∇
2
[(m
2
−∇
2
)
2
+λφ
2
]
φ +
N (2.4.11)
The first term on the R.H.S. is known as the streaming term or reversible term in
the equation of motion. The obvious question is what does the streaming term do
to the equilibrium distribution. The answer is that the equilibrium distribution is
not affected by the streaming term. This is easy to see on constructing
dF
dt
using
Eqns.(2.4.1) and (2.4.10). We find
dF
dt
=0
since
φ.
˙
φ =g
φ.(
φ ×∇
2
φ)
is trivially zero. Thus the streaming term does not disturb the equilibrium distri-
bution. The model we have just described is model J in the notation of Halperin
and Hohenberg.
We now turn to a different critical system where we will find that we need two
Langevin equations. This is the liquid-gas critical point or the consolute point in a
binary liquid. The liquid-gas critical point is the usual Van der Waals critical point
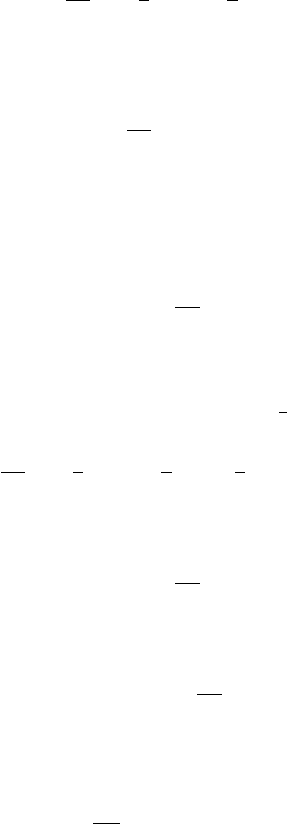
2.4 Dynamics of a Magnet near Its Critical Point 39
which is very familiar. The transition at the consolute point of a binary liquid is
similar to the liquid-gas critical point. Above the consolute point, the two liquids
in the binary mixture are completely miscible while below the critical temperature
they separate and a meniscus is formed. The order parameter for the transition is the
scalar field φ(r,t) which is the fluctuation of the local concentration of one of the
binary liquid components from the concentration required for complete miscibility.
As in the case of the ferromagnet, the statics is described by the free energy,
F =
d
D
r
m
2
2
φ
2
+
1
2
(
∇φ)
2
+
λ
4
(φ)
4
(2.4.12)
There is a conservation law for concentration and hence the equation of motion for
the order parameter is
˙
φ =∇
2
δF
δφ
+N (2.4.13)
Now comes the question whether the above equation is complete. One is discussing
fluids and fluctuations, so there would be fluctuations in the velocity - although
there is no overall flow there will always be a fluctuating velocity field and the
velocity will carry the concentration field, so that the above equation will become
˙
φ =−(v.
∇)φ +∇
2
δF
δφ
+N (2.4.14)
But now we have coupled to an additional field in the streaming term (v.
∇)φ [this
additional term did not come in the ferromagnet] the free energy expression of
Eq.(2.4.12) has to be modified to include the kinetic energy
1
2
ρv
2
and we have
˜
F =
d
D
r
m
2
2
φ
2
+
1
2
(
∇φ)
2
+
λ
4
(φ)
4
+
1
2
ρv
2
(2.4.15)
The equation of motion in Eq.(2.4.14) simply becomes
˙
φ =−(v.
∇)φ +∇
2
δ
˜
F
δφ
+N (2.4.16)
How about the equation of motion for v? We expect
˙v
i
=Streaming term +ν∇
2
δ
˜
F
δv
i
+N
v
i
(2.4.17)
What determines the streaming term? The streaming term has to be determined so
that
d
˜
F
dt
=0
