Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.

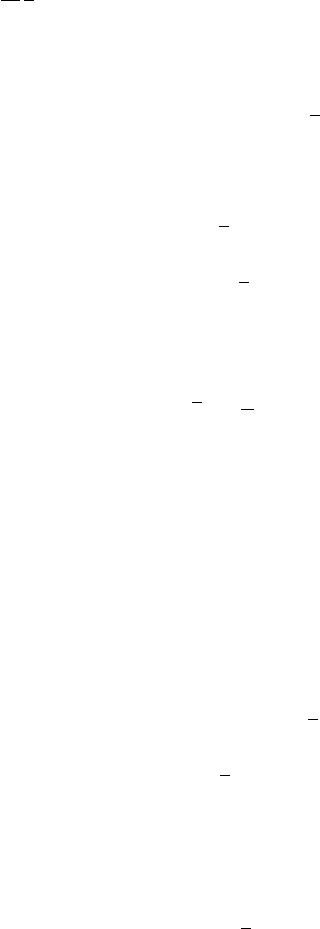
8.8 Dynamical Systems and Turbulence 273
For the inviscid and unforced flow, the total energy is conserved. This condition
can be written as
0 =
d
dt
1
2
N
m=1
i
U
m
i
U
m
i
=
N
m=1
i
U
m
i
˙
U
m
i
=
N
m=1
2
N−m
U
m
˙
U
m
(8.8.26)
Imposition of this condition leads to
˙
U
n
= 2
−n(1+D/2)
U
n−1
U
n−1
−
1
2
2
−3D/2
U
n
U
n+1
+α
U
n−2
U
n−2
− 2
−3D/2−2
U
n
U
n+2
+β
U
n
U
n−1
−
1
2
2
−3D/2
U
n+1
U
n+1
+γ
U
n−1
U
n−2
−
1
2
2
−3D/2
U
n−1
U
n+1
(8.8.27)
Now, suppose that at time t =0, U
n
=0 for all n ≤m. In that case, Eq.(8.8.27)
becomes
˙
U
m
=2
−m−m
D
2
−
β
2
2
−3D/2
U
m+1
U
m+1
(8.8.28)
We see that U
m
will be excited by U
m+1
and there will be a transfer of energy
from large scale modes to smaller scale modes - a forward energy cascade. In a
similar fashion if U
n
=0 for all n ≥m at t =0, then
˙
U
m
=2
−m−mD/2
U
m−1
U
m−1
+αU
m−2
U
m−2
+γU
m−1
U
m−2
(8.8.29)
This represents a flow of energy from lower scales to higher scales - a backward
cascade of energy. We now introduce a further simplification in Eq.(8.8.27) - only
one forward cascade and one backward cascade will be kept. This leads to,
˙
U
n
= 2
−n(1+D/2)
U
n−1
U
n−1
−
1
2
2
−3D/2
U
n
U
n+1
+β
U
n
U
n−1
−
1
2
2
−3D/2
U
n+1
U
n+1
(8.8.30)
We now choose β =−2
p
which assures us that if U
n
> 0 at any time, it will remain
non negative at all subsequent times. This can be seen by considering a point of
time at which U
n
=0. Then,
˙
U
n
=2
−n(1+D/2)
U
n−1
U
n−1
+
1
2
2
p−3D/2
U
n+1
U
n+1
> 0 (8.8.31)
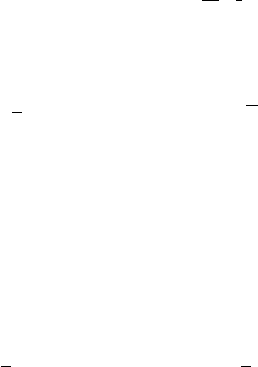
274 8 Turbulence
Clearly, Eq.(8.8.30) has a fixed point solution, U
n
∝2
nD
2
+
n
3
independent of the
value of p. This fixed point corresponds to the Kolmogorov spectrum since the
total energy contained in a shell of scale n is
k
0
2
−(n+1)
k
0
2
−n
E(k)dk =
1
2
n
[U
n
]
2
∼2
(N−n)D
2
nD+
2n
3
(8.8.32)
If E(k) ∼k
−α
, then α =5/3.
We can absorb the factor 2
−3D/2
by a redefinition of the U as U 2
nD/2
and the
resulting equation is precisely that used as a starting point by Carbone (a superficial
difference in the position of the factor 2 in the coefficient of U
n+1
U
n+1
occurs
because our k
n
=k
0
/2
n
as opposed to k
n
=k
0
2
n
used by others) when the linear
energy dissipating term and the forcing term are introduced. Since the Kolmogorov
spectrum is obtained for all p, we can choose p =0 and write for n ≤N
˙
U
n
= k
n
(U
n−1
U
n−1
−
1
2
U
n
U
n+1
) −k
n
(U
n
U
n−1
−
1
2
U
n+1
U
n+1
)
=−νk
2
n
U
n
+δ
n,N
(8.8.33)
Where −νk
2
n
U
n
represents the viscous loss and δ
n,N
is the term which signifies
that in the N
th
shell (large length scale) there is an extra forcing coming from
outside.
References
1. A.N. Kolmogorov, C R (Dokl) Acad. Sci. USSR, 30, 301, (1941)
2. H.L. Grant, R.W. Stewart and A. Moillet, J. Fluid. Mech., 12, 241, 1962; 13, 237,
(1962)
3. A.S. Monin and A.M. Yaglom, Statistical Fluid Mechanics, Vol.2, MIT Press, (1971)
4. H. Tennekes and I. Lumley, A First Course in Turbulence,MIT Press Cambridge, (1972)
5. D.C. Leslie, Developments in the Theory of Turbulence, Clarendon Press, Oxford,
(1972)
6. S.A. Orszag, Les Houches Lectures on Fluid Dynamics, Gordon and Breach, London,
(1973)
7. D. Forster, D. Nelson and M. Stephen, Phys. Rev. A16, 732, (1976)
8. P.C. Martin and C. De Dominicis, Prog. Theor. Phys. (Suppl.) 64, 108, (1978)
9. C. De Dominicis and P.C.Martin, Phys. Rev. A19, 419, (1979)
10. C. Meneveau and K.R. Sreenivasan Phys. Rev. Lett., 59, 1424, 1987; Nucl. Phys. (Proc.
Suppl.), B2, 49, (1987)
11. M. Lesieur, Turbulence, M Ninjhuis, Amsterdam, (1988)
12. kn:comb W.D. McComb, The Physics of Fluid Turbulence, Clarendon Press, Oxford,
(1990)
13. L. Sirovich ed., New Perspectives in Turbulence, Springer-Verlag, Berlin, (1990)
14. E. Ott, Chaos in Dynamical Systems, Cambridge University Press, (1993)
15. U.Frisch, Turbulence, Cambridge University Press, (1996)

9
Polymers
9.1 Introduction
A polymer is a large molecule made up of many small chemical units joined
together by some chemical bond. Most artificially produced polymers are a repet-
itive sequence of a particular atomic group and take the form -A-A-A-. The basic
unit (A in the example) is called a monomer and the number of monomer units
in a polymer is usually called its degree of polymerization. A polymer molecule
has a large number of internal degrees of freedom and so can take many different
configurations. It is because of these configurations, that statistical mechanics can
be applied even to a single polymer chain. An easy way of picturing the polymer
is to imagine it lying on a regular lattice.
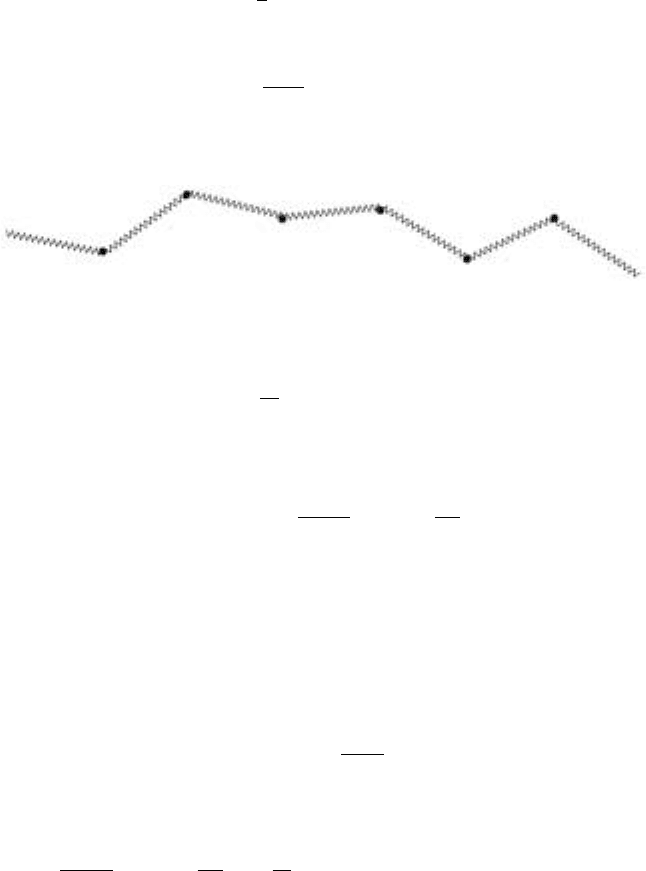
The circles at some of the lattice points represent the monomer units and the
heavy lines along the lattice connecting the circles are the bonds. We assume that
the bonds are free to orient themselves in any manner. So all directions have equal
probability and the statistics of the polymer configurations is the same as that of a
random walk. One of the main issues is the average end to end distance R on the
degree of polymerization N. The polymer in the Fig. 9.1 is made up of N bonds.
If the radius vector of the n
th
bond is r
n
, then the “end-to end” vector
R will be
R =
n
r
n
(9.1.1)
Clearly,
R=0 and hence it is R
2
which one calculates.
R
2
=
m
n
r
m
.r
n
= b
2
δ
mn
= Nb
2
(9.1.2)

276 9 Polymers
Figure 9.1. A polymer lying along a regular lattice
One can calculate the probability distribution of
R. We consider a N-monomer
polymer with one end pegged at r =0. The probability of the other end being
at
R is P(
R, N). If the coordination number of the lattice (i.e. number of nearest
neighbours) is Z, and if b
i
(i =1, 2....Z) are the possible bond vectors that a polymer
may take then if the polymer has reached
R after N steps, then after N −1 steps
it could have been at any of
R −
b
i
and the probability of being at any of these
positions is 1/Z. Thus,
P(
R, N) =
1
Z
Z
i=1
P(
R −
b
i
,N−1) (9.1.3)
If N 1 and |
R||
b
i
|, we can expand the R.H.S and write
P(
R, N) = P(
R, N) −
1
Z
Z
i=1
∂P
∂N
−
1
Z
Z
i=1
b
iα
∂P
∂R
α
+
1
2Z
Z
i=1
b
iα
b
iβ
∂
2
P
∂R
α
∂R
β
+..... (9.1.4)
Now,
1
Z
Z
i=1
b
iα
= 0
and
1
Z
Z
i=1
b
iα
b
iβ
=
b
2
3
δ
αβ
From Eq.(9.1.4), we then get the differential equation,
∂P
∂N
=
b
2
6
∂
2
P
∂R
2
(9.1.5)

9.1 Introduction 277
with the boundary condition that
R =0, if N =0, we have the solution
P(
R, N) =
3
2πNb
2
3/2
e
−
3
2
R
2
Nb
2
(9.1.6)
The probability distribution of R is Gaussian.
The assumption that the orientation of each bond is random is clearly not
realistic. It allows the polymer to fold back on to itself at certain locations which
is not allowed. One can remedy this by disallowing doubling back, which means
that the bond vector r
n+1
is not allowed to point back, that is it cannot be −r
n
,but
can take any of the other Z −1 configurations with equal probability. With this
constraint the average used in deriving Eq.(9.1.2) becomes
r
n
.r
m
=
b
2
(z −1)
|n−m|
(9.1.7)
With the correlations falling off one still gets
R
2
=Nb
2
eff
(9.1.8)
where b
2
eff
can be obtained from b
2
.
The distribution for R is always Gaussian for such chains. Interactions which
may occur between two monomer units which are in close proximity along the
length of the chain are called short range interactions. In ideal chains (no long
range interactions), the relation R
2
∝N always holds.
The major change occurs when we put in long range interactions. The main
interaction is the excluded volume effect, which means no two monomers can be
at the same point in space. Consequently, as the chain winds around two monomer
units, however far they may be along the length of the chain, they repel each other
equally strongly when they come close to each other. This excluded volume inter-
action which is genuinely long ranged changes the relation between R
2
and N.
We now move away from lattice models and introduce the gaussian model
based on the experience of the lattice. The Gaussian model assumes that the bond
vector r itself possesses some flexibility and follows a Gaussian distribution
p(r) =
3
2πb
2
3/2
exp
−
3
2
r
2
b
2
(9.1.9)
If the position of the n
th
monomer is
R
n
and that of the (n +1)
th
monomer
is
R
n+1
, the probability distribution of the set of position vectors {
R
n
}=
(
R
0
R
1
......
R
N
) is
P({
R
n
}) =
3
2πb
2
3N/2
exp
−
3
2b
2
N
n=1
(
R
n
−
R
n+1
)
2
(9.1.10)
278 9 Polymers
One can think of the Gaussian chain as a linkage of monomers consisting of har-
monic springs. If K is the spring constant, the energy of the chain can be written
as
E =
1
2
K
N
n=1
(
R
n
−
R
n+1
)
2
(9.1.11)
with the equilibrium state of the chain given by exp{−E/K
B
T }, if the spring con-
stant K can be chosen to be K =
3K
B
T
b
2
. Because of the connection with springlike
behaviour, the gaussian chain, pictured in Fig 9.2, is often called a bead spring
model We can write a continuum form of the probability distribution given by
Figure 9.2. A bead and spring model of the polymer
identifying (
R
n
−
R
n+1
)
2
with (
∂
R
∂τ
)
2
where τ is a coordinate along the length of
the chain. The probability distribution for a particular
R(τ) is then given by the
path integral
P(
R(τ))∝exp
⎧
⎨
⎩
−
3
2K
B
T
N
0
dτ
!
∂
R
∂τ
"
2
⎫
⎬
⎭
(9.1.12)
This is the probability distribution for the ideal chain. Now we need to include the
excluded volume effect. The interaction is between
R(τ) and
R(τ
), when the two
vectors are very close regardless of where τ and τ
are. We put in an absolutely
short range interaction which would be a delta function interaction represented by
v
0
δ(
R(τ) −
R(τ
)). The probability distribution of Eq.(9.1.12) can now be written
as
P ∝exp
−
F
K
B
T
(9.1.13)
where
F =
3
2K
B
T
N
0
dτ
!
∂
R
∂τ
"
2
+
v
0
2
N
0
dτ
N
0
dτ
δ(
R(τ) −
R(τ
)) (9.1.14)
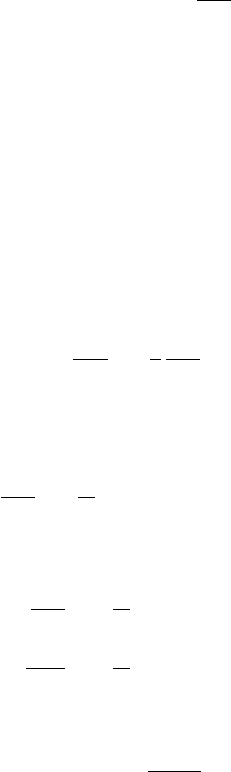
9.1 Introduction 279
With the statics set up as shown, we can now write the dynamics around the
equilibrium state in the form of a Langevin equation
˙
R
α
(τ ) =−
δF
δR
α
+N
α
where N
α
(τ, t)N
α
(τ
,t)=2K
B
Tδ
αβ
δ(τ −τ
)δ(t−t
) (9.1.15)
This dynamics can become extremely complicated because of the long range in-
teraction.
We will also be considering the question of interaction of the polymer with the
solvent and the resulting inter monomer interaction mediated by the solvent. For
hydrophobic monomers, this interaction can cause the polymer to fold itself into a
ball to avoid the water contact, while for hydrophillic contacts, the polymer chain
is expected to swell.
Returning to the bead spring model if we focus on the dynamics of a particular
bead, say the bead located at
R
n
, then the Langevin dynamics of that bead will be
governed by the equation of motion
d
R
n
dt
=−
1
ζ
∂E
∂
R
n
+g
n
(9.1.16)
where ζ is the coefficient of friction of a bead. Using E from Eq.(9.1.11) we can
write, for the intermediate beads (n =1, 2....N −1)
d
R
n
dt
=−
K
ζ
(
R
n+1
+
R
n−1
−2
R
n
) +g
n
(9.1.17)
For the beads at the two end-points n =0 and n =N,
d
R
0
dt
=−
K
ζ
(
R
1
−
R
0
) +g
0
(9.1.18)
d
R
N
dt
=−
K
ζ
(
R
N−1
−
R
N
) +g
N
(9.1.19)
In the above
K =
3K
B
T
b
2
.
In order to cast the above equation in the same form as Eq.(9.1.17), we can write
R
−1
=
R
0
R
N+1
=
R
N
(9.1.20)
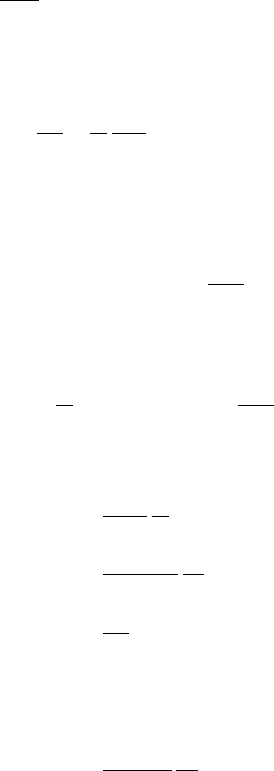
280 9 Polymers
in which case Eq.(9.1.18) holds for n =0, 1, ......N with the end-point (boundary)
conditions
∂
R
N
dt
=0, for n =0,N (9.1.21)
if we think of n as continuous rather than a discrete variable. In this picture of
continuously varying n, the equation of motion becomes
∂
R
dt
=
K
ζ
∂
2
R
∂n
2
+g(n, t) (9.1.22)
with the above boundary conditions.
The solution for
R(n, t) can be obtained in terms of the normal modes
X
p
(t).
The normal modes are introduced through the relation
R(n, t) =
p
X
p
(t) cos
np π
N
(9.1.23)
where p =0, 1, 2...... The inversion of this relation yields
X
p
(t) =
1
N
N
0
dn
R(n, t) cos
nπp
N
(9.1.24)
Inserting the normal mode expansion in Eq.(9.1.22), we find
˙
X
p
(t) =−
p
2
π
2
N
2
K
ζ
X
p
+g
p
=−
3π
2
K
B
T
N
2
b
2
p
2
ζ
+g
p
=−
X
p
τ
p
+g
p
(9.1.25)
where we have used the value of K from Eq.(9.1.19) and the relaxation rate τ
p
for
the p
th
mode is written as
τ
p
=
ζN
2
b
2
3π
2
k
B
T
1
p
2
(9.1.26)
The random force g
p
has zero mean and its variance is prescribed as
g
pα
(t)g
qβ
(t
)
=k
B
Tδ
pq
δ
αβ
δ(t −t
) (9.1.27)
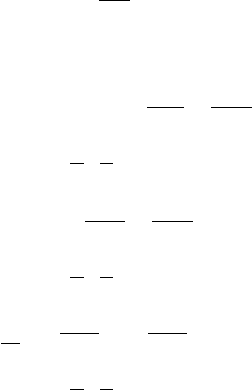
9.1 Introduction 281
The solution of Eq.(9.1.25) can be written as
X
pα
(t) =
t
0
e
−
(t−t
)
τ
p
g
pα
(t
)dt
+X
pα
(0)e
−t/τ
p
(9.1.28)
The correlation functions can be found as
X
pα
(t
1
)X
qβ
(t
2
)
=
t
1
0
dt
t
2
0
dt
e
−
(t
1
−t
)
τ
p
e
−
(t
2
−t
)
τ
q
g
pα
(t
)g
qβ
(t
)
+e
−
t
1
τ
p
+
t
2
τ
q
X
pα
(0)X
qβ
(0)
=
t
2
0
dt
e
−
(t
1
−t
)
τ
p
e
−
(t
2
−t
)
τ
p
+e
−
t
1
τ
p
+
t
2
τ
q
X
pα
(0)X
qβ
(0)
=
τ
p
2
e
−
(t
1
−t
2
)
τ
p
−e
−
(t
1
+t
2
)
τ
p
+e
−
t
1
τ
p
+
t
2
τ
q
X
pα
(0)X
qβ
(0)
(9.1.29)
If t
1
−t
2
=τ and τ is large then,
X
pα
(t +τ)X
qβ
(t)
=e
−τ/τ
p
δ
pq
δ
αβ
(9.1.30)
This is true if p =0. If p =0, then τ
p
→∞, and Eq.(9.1.28) yields
X
0α
(t) −X
0α
(0) =
t
0
g
0α
(t
)dt
(9.1.31)
Consequently,
[X
0α
(t) −X
0α
(0)][X
0β
(t) −X
0β
(0)]
=
t
0
dt
t
0
dt
g
0α
(t
)g
0β
(t
)
= δ
αβ
t
0
dt
= δ
αβ
t (9.1.32)
We can now investigate various physical quantities associated with the polymer dy-
namics. First let us look at the centre of mass motion. The centre of mass coordinate
R
CM
is

282 9 Polymers
R
CM
(t) =
1
N
N
0
dn
R(n, t)
=
1
N
N
0
dn
p
X
p
(t) cos
nπp
N
=
1
N
p
X
p
(t)
N
pπ
δ
p0
= X
0
(t) (9.1.33)
Hence
[
R
CM
(t) −
R
CM
(0)]
2
=
[X
0
(t) −X
0
(0)]
2
= t (9.1.34)
The centre of mass diffuses with a diffusion constant
D
CM
=
k
B
T
Nζ
,
which is inversely proportional to N.
If one wants to look at the rotational motion of the polymer as a whole, then
one needs to look at the end-to-end distance vector
R(t) defined as
R(t) =
R(N, t) −
R(0,t)
=
p
X
p
(t)(cos pπ −1)
=−
p
X
p
(t)2 sin
2
pπ
2
=−4
positive
p, odd
X
p
(t) (9.1.35)
The correlation function for
R(t) can be written as
R
α
(t)R
α
(0)
= 16
p odd
X
pα
(t)X
pα
(0)
= Nb
2
p odd
8
p
2
π
2
e
−t/τ
p
(9.1.36)
The smallest τ
p
will dominate in the above series and hence the rotational relaxation
rate is
τ
1
=
ζN
2
b
2
3π
2
k
B
T
Nb
2
D
CM
