Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium
Подождите немного. Документ загружается.

8.5 Advection of a Passive Scalar 253
the correct Kolmogorov limit. In this problem, one has the dissipative anomaly
because lim
κ→0
κ(
∇φ)
2
would be finite and dissipating the scalar energy density
E =
1
2
φ
2
. The energy balance reads,
∂
t
Ed
D
r =
[fφ−κ(
∇φ)
2
]d
D
r (8.5.7)
The stationarity condition allows one to form equations for the n-point correlation
functions analogous to those exhibited in Eq.(8.4.28). In this case they are simpler
and have the form
M
κ
N
φ(x
1
)φ(x
2
)...φ(x
N
)
=
1
2
j,k
C(x
j
−x
k
)φ(x
1
)φ(x
2
)..φ(x
j
)..φ(x
k
)..φ(x
N
) (8.5.8)
where symbols which have a bar over them are missing in the correlation function.
The operator M
κ
N
is given by
M
κ
N
=−κ
N
j=1
∇
2
x
j
+
1
2
j,k
d
ab
(x
j
−x
k
)∇
a
x
j
∇
b
x
j
(8.5.9)
In the inertial range κ →0 and
M
0
N
=
1
2
j,k
d
ab
(x
j
−x
k
)∇
a
x
j
∇
b
x
j
(8.5.10)
Let us now look at the two point correlation function φ(x)φ(
0). Exploiting
translational invariance
M
0
2
=−D
0
(D −1)
1
r
D−1
d
dr
r
D+ζ −1
d
dr
(8.5.11)
In this case, it is now easy to see that [φ(x)−φ(
0)]
2
will scale as r
2−ζ
, which
is exactly as the naive dimensional analysis predicts. The non-trivial nature of
the problem shows up in the higher order structure factors when it is seen that
[φ(x)−φ(
0)]
N
=r
(2−ζ)N/2
. Instead, they behave as
[φ(x)−φ(
0)]
N
A
N
L
r
ρ
N
r
(2−ζ)N/2
(8.5.12)
where
ρ
N
=ζ
N(N −2)
2(D +2)
+0(ζ
2
) (8.5.13)

254 8 Turbulence
or
ρ
N
=ζ
N(N −2)
2D
+O
1
D
2
(8.5.14)
for large D.
Instead of describing the calculations leading to Eqns.(8.5.13) and (8.5.14) we
show how non-trivial exponent can arise even for N =2 in a slightly different
model. Here an additional friction term is used and we have
∂
t
φ +(v.
∇)φ +
φ
τ
−κ∇
2
φ =f (8.5.15)
For N =2, the correlation function F
2
=φ(x)φ(
0) satisfies in the limit κ =0
(see Eq.(8.5.8)) for ζ =2,
C(r) =−D
0
(D −1)
1
r
D−1
d
dr
r
D+1
d
dr
F
2
+
2
τ
F
2
(8.5.16)
This can be solved by factorizing
F
2
(r) =G(r)H (r) (8.5.17)
where G(r) satisfies the homogeneous equation
−D
0
(D −1)
1
r
D−1
d
dr
r
D+1
d
dr
G(r) +
2
τ
G(r) =0 (8.5.18)
This has the solution G(r) ∼r
α
, where
−D
0
(D −1)α(D +α) +
2
τ
= 0
or α
2
+Dα −
2
τD
0
(D −1)
= 0
giving the roots α
±
=−
D
2
±
D
2
4
+
2
D
0
(D −1)τ
(8.5.19)
The boundary condition that F
2
(r) is finite at r =0, eliminates α
−
and now H(r)
can be found as the solution of
D
0
(D −1)
r
D−1+α
d
dr
r
D+1+2α
dH
dr
=C(r) (8.5.20)
The solution for
F
2
(r) =r
α
+
∞
r
1
D
0
(D −1)
dρ
ρ
D+1+2α
ρ
0
r
D−1+α
C(r)dr (8.5.21)
8.6 Intermittency Phenomenology 255
For small r, this has the behaviour
F
2
(r) ∼r
α
+
(8.5.22)
which is to be contrasted with the na
¨
ıve scaling behaviour which for ζ =2is
F
2
(r) ∼r
(0)
(at most logarithmic terms). The anomalous dimension has arisen
from the zero mode of the stationarity condition. This illustrates the general result
that the root cause of the anomalous dimensions lies in the zero modes of the
stationarity condition.
8.6 Intermittency Phenomenology
As we have already discussed before, the phenomenon of intermittency has to do
with the occurrence of the anomalous scaling (Eq.(8.2.7)) in the velocity structure
functions. Soon after the publication of Kolmogorov’s work in 1941 it was pointed
out by Landau that the dissipation which is determined by the fluctuations of the
derivative of the random velocity field may not be constant. The local dissipation
can be defined as
(x) =ν
over a ball
surroundingx
d
D
r
∂v
i
∂x
j
∂v
i
∂x
j
(8.6.1)
and experimentally measured with great accuracy. The correlation function
(x)(x +r) in the Kolmogorov analysis has to be determined by ¯ and r alone
and hence
(x)(x +r)=( ¯)
2
(8.6.2)
The experimental results clearly supported a power law
(x)(x +r)=( ¯)
2
L
r
µ
(8.6.3)
where µ is a small exponent (µ 0.20) and is called the intermittency exponent.
The experimentally observed signal shows rare but large fluctuations in the dis-
sipation and hence the phenomenon is known as intermittency. The effect of this
fluctuation on the velocity correlation function was first considered by Obukhov
and Kolmogorov in 1962, when it was assumed that the dissipation rate ¯ has
a log-normal distribution. The width of the distribution was conjectured from a
perturbative calculation to be of the form
σ
2
=A +9δ ln
L
r
(8.6.4)

256 8 Turbulence
where δ is a universal constant. With the mean of the distribution given by m,it
follows that
p/3
=e
pm/3
e
p
2
σ
2
/18
(8.6.5)
The velocity difference v
r
at scale r is related to the local
r
by v
r
=(r
r
)
1/3
and hence
|v
r
|
p
= Const ×r
p/3
(
r
)
p/3
= Const ×r
p/3
e
pm/3
e
p
2
(A+9δ ln
L
r
)
(8.6.6)
For p =3, we have an exact result and that fixes m as follows:
|v
r
|
3
= Const ×re
m
e
σ
2
/2
= Const ׯr (8.6.7)
which identifies
¯ =e
m+
σ
2
2
Returning to Eq.(8.6.6) and using Eq.(8.6.7)
|v
r
|
p
= Const ×r
p/3
e
m+σ
2
/2
p/3
e
−
pσ
2
6
+
p
2
σ
2
18
= Const ×r
p/3
¯
p/3
e
p(p−3)(A+9δ ln
L
r
)/18
= Const ×r
p/3
¯
p/3
e
p(p−3)
2
δ ln
L
r
= C
p
¯
p/3
r
p/3
L
r
p(p−3)
2
δ
(8.6.8)
For p =6
|v|
6
=C
6
¯
2
r
2
L
r
9δ
Noting that
r
∼|v
r
|
3
/r,
the dissipation correlation function goes as
2
r
∝r
−9δ

8.6 Intermittency Phenomenology 257
which gives
µ =9δ (8.6.9)
In the above phenomenology, it is clear that once δ is fixed, all other exponents
follow. It is reasonably safe to say that experiments show deviation from Obukhov-
Kolmogorov phenomenology for high value of p.
The information regarding the dissipation spectrum can be looked at from
another point of view. In the inviscid limit, the Navier-Stokes equation is invariant
under the rescaling,
x →x
= λx
t →t
= λ
1−α/3
t
v →v
= λ
α/3
v (8.6.10)
for any α. Now the local dissipation rate is
r
∼v
3
r
/r and hence scales as λ
α−1
.
This would mean that
r
L
∼
r
L
α−1
(8.6.11)
The constancy of
r
in the Kolmogorov picture now suggests α =1 in three dimen-
sional space.
The reality however, is that α is not constant and α takes on different values
on different interwoven fractal subsets of the three dimensional space in which the
dissipation field is embedded. The set on which the scaling exponent lies α and
α +dαis characterized by the fractal (Hausdroff ) dimension f(α). Experimentally
f(α)vs. α can be measured. We would like to indicate how this is done.
The total dissipation in a volume r
D
is E
r,D
and can be written as
E
r,D
=
r
r
D
∼r
α−1+D
(8.6.12)
We divide the entire space into boxes of size r. What is measured is E
r,D
in each
box and what is constructed from it is the sum of
boxes
E
q
r,D
. This quantity is
supposed to scale with r in the fashion
boxes
E
q
r,D
∼ r
(q−1)D
q
or
boxes
r
(α−1+D)q
∼ r
(q−1)D
q
(8.6.13)
The generalized dimensions D
q
defined through Eq.(8.6.13) constitute a measure of
the spottiness of the dissipation process. Uniform dissipation over all space would
correspond to D
q
being independent of q. The sum over boxes can be replaced by
an integration if we note that the number of boxes in which α lies between α and
dα is proportional to r
−f
D
(α)
and thus Eq.(8.6.13) becomes
258 8 Turbulence
ρ(α)r
q(α−1+D)
r
−f
D
(α)
dα ∼r
(q−1)D
q
(8.6.14)
As r →0, we can evaluate the integral by steepest descent and one then has
q(α −1 +D) −f
D
(α) = (q −1)D
q
if
∂f
D
(α)
∂α
= q
and
∂
2
f
D
(α)
∂α
2
< 0 (8.6.15)
From Eq.(8.6.15)
f
D
(α) = αq −(q −1)(D
q
−D +1) +D −1
and α =
d
dq
[(q −1)(D
q
−D +1)] (8.6.16)
The experiments measure D
q
and from that one infers α and f(α). Note that for
D =1
α =
d
dq
[(q −1)D
q
]
f(α) = αq −(q −1)D
q
(8.6.17)
The experiments probe the projection along a given direction. A line segment is
divided into bins of size n and E
r
is determined from each bin. One then forms
Z
q
=
E
q
r
for each value of r (it is seen that the slope of ln E
r
vs ln r is different
for different bin locations showingα has a distribution) and ln z
1
q−1
q
vs ln r isplotted.
The slope yields D
q
from which α and f(α)are obtained using Eq.(8.6.17) because
a one dimensional section is being considered. A typical f(α) curve is shown in
Fig. 8.6 We note from Eq.(8.6.11), that
α =
ln
r
L
ln
r
L
+1 (8.6.18)
and consequently the probability distribution P
(
r
) for the dissipation can be
written as
P
(
r
) =P
α
(α)
dα
d
r
/P (
r
=0) (8.6.19)
where P(
r
=0) is the probability that
r
is non-zero for non-zero r i.e. a box of
size r always contains a part of the multifractal. In terms of the fractal dimension
D
0
, the probability of having a box of size r being occupied by the multifractal is
P(
r
=0) =C
1
r
L
(D−D
0
)
(8.6.20)
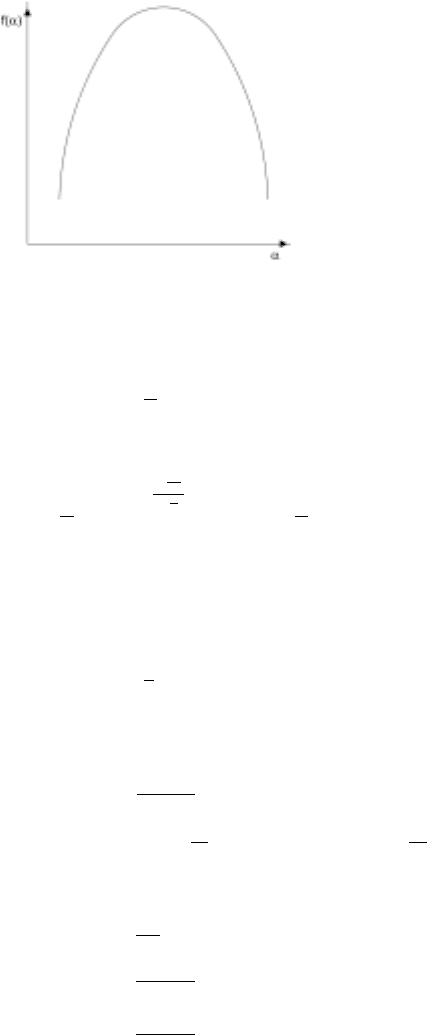
8.6 Intermittency Phenomenology 259
Figure 8.6. A typical distribution of the scaling indices
In a box of length r, the probability density for α lying between α and α +dα is
P
α
=C
2
r
L
D−f
D
(α)
(8.6.21)
Using Eqns.(8.6.17)-(8.6.20)
P
(
r
) =C
r
L
D
0
−f
D
ln
r
L
ln
r
L
+1
×
r
ln
r
L
−1
Since f
D
(α) is known from the experiment, this is the way the dissipation proba-
bility distribution is experimentally found out. How close is this to the log-normal
distribution assumed by Obukhov and Kolmogorov? To understand this, we assume
that the f(r)vs α curve shown in Fig. 8.6 can be approximated by a parabola as
f(α)=f(α
0
) +
1
2
(α −α
0
)
2
f
(α
0
) (8.6.22)
where, α =α
0
is the point where the f(α) vs α curve has its maximum. The
maximum value is the fractal dimension D
0
of the support and hence
f(α)=D
0
+
f
(α
0
)
2
(α −α
0
)
2
(8.6.23)
We note that from Eq.(8.6.15) that for q →1,
∂f
∂α
=1 where α
1
=lim
q→1
d
dq
[(q −
1)D
q
].InD =1, Eq.(8.6.17) shows f(α
1
) =α
1
. Thus at the point α =α
1
, the f(α)
vs α has to be tangent to the line f(α)=α. For the parabolic approximation,
q =
df
dα
=f
(α
0
)(α −α
0
)
leading to α =
q
f
(α
0
)
+α
0
and α
1
=
1
f
(α
0
)
+α
0

260 8 Turbulence
At α =α
1
, the parabolic approximation leads to
α
1
=f(α
1
) = D
0
+
f
(α
0
)
2
(α
1
−α
0
)
2
= D
0
+
1
2
1
f
(α
0
)
On the other hand α
1
=α
0
+
1
f
(α
0
)
and thus we are led to
1
2f
(α
0
)
=−(α
0
−D
0
)
giving
f(α)=D
0
−
1
4
(α −α
0
)
2
α
0
−D
0
(8.6.24)
If we substitute the above f(α) into Eq.(8.6.21), then the distribution P
(
r
) is
log-normal with the mean m and the variance σ
2
given by
m = ln
L
−(α
0
−1) ln
L
r
σ
2
= 2(α
0
−D
0
) ln
L
r
(8.6.25)
In this approximation the intermittency exponent µ is given by
µ =2(α
0
−D
0
) (8.6.26)
Thus the deviation of the log-normal distribution from the real distribution is mea-
sured by the deviation of f(α)vs α curve from a parabolic form.
Realizing that the underlying set on which the dissipation is occurring is a
multifractal, Sreenivasan and Menevau came up with a physical picture of energy
transmission process which produces a multifractal distribution. This is pictured in
Fig. 8.7 We have taken a one dimensional slice of the process and a large (scale L)
energy containing eddy is shown dividing its energy into two eddies (scale L/2).
The division however, does not occur equally
- the left hand receives a fraction p
1
while the right hand side receives a fraction p
2
with p
1
+p
2
=1.
Todetermine the characteristics of this process, we need to compute the quantity
E
q
r
where the sum is over the different eddies of size r at a scale r =
L
2
n
and q
is an arbitrary integer. We expect,
E
q
r
=E
q
r
L
(q−1)D
q
(8.6.27)
The set is a standard fractal if D
q
is independent of q and multifractal if D
q
is a
non-trival function of q. From the figure, it is clear that

8.6 Intermittency Phenomenology 261
Figure 8.7. The breaking up of an energy containing eddy
E
q
r
=
m
E
qn
C
m
p
q
1
m
p
q
2
n−m
= E
q
p
q
1
+ p
q
2
n
(8.6.28)
From Eq.(8.6.27)
E
q
r
=E
q
1
2
n
(q−1)D
q
leading to
D
q
=−
1
q −1
ln
2
p
q
1
+ p
q
2
(8.6.29)
With p
1
chosen to fit one of the moments, the indices D
q
are known for all the
moments and it was found by Menevau and Sreenivasan that p
1
=0.7 accounts
for the data on the all the different correlation functions.
A formula for the scaling behaviour of the n-point correlation function was
found by She and Leveque based on heuristic arguments depending on a picture of
the coherent structures in the problem. The velocity correlation can be written
|v(x +r)−
(x)|
n
∝
n
r
n/3
r
ζ
n
(8.6.30)
here the anomalous dimension exponents ζ
n
are given by
ζ
n
=−
2
9
n +2
1 −
2
3
n
(8.6.31)
and are seen to be universal numbers. The above formula for ζ
n
fits the experimental
result very well and it is a theoretical challenge to derive ζ
n
from the Navier-Stokes
equation.

262 8 Turbulence
8.7 Perturbation Theory
In this section, we show what happens in different approaches to diagrammatic
perturbation theory. For this purpose, we return to Eqns.(8.1.9)-(8.1.11). The two
quantities we focus on are the response function G(k, ω) and the correlation func-
tion C(k,ω) defined as
P
αβ
=
∂v
α
(k, ω)
∂f
β
(k
,ω
)
δ(
k +
k
)δ(ω +ω
)
−1
(8.7.1)
and
P
αβ
C(k,ω) =v
α
(k, ω)v
β
(k
,ω
)
1
δ(
k +
k
)δ(ω +ω
)
(8.7.2)
In the absence of the nonlinearity in Eq.(8.1.9), the response function is G
0
(k, ω)
given by
G
−1
0
(k, ω) =−iω +νk
2
(8.7.3)
The nonlinearity changes G
0
to the full G by Dyson’s equation which reads
G
−1
(k, ω) =−iω +νk
2
+(k,ω) (8.7.4)
The physical interpretation of is a relaxation rate. Treating the nonlinearity
perturbatively, the one loop contribution
(1)
(k, ω) to is given by
(1)
(k, ω) =
d
D
p
(2π)
D
dω
2π
M
αβγ
(k) M
σνα
(k) P
βσ
(p)P
νγ
(
k −p)
×G
0
(p, ω
)C
0
(
k −p, ω −ω
) (8.7.5)
where C
0
(k, ω) is the zeroth order correlation function, which is clearly |G(k, ω)|
2
ff .
We now introduce an approximation known as self-consistent mode coupling
and anticipate that in the Kolmogorov (scaling) limit, the contribution of the non-
linear terms to the self-energy will dominate the molecular viscosity diffusion rate
νk
2
. Thus Eq.(8.7.4) becomes
G
−1
=−iω +(k, ω) (8.7.6)
For the self-consistent mode coupling approximation, one makes the assumption
that replacing G
0
and C
0
on the R.H.S of Eq.(8.7.5) by the full response function
G and the full correlation function C leads to the full self-energy . Thus the
self-consistent mode coupling involves in the diagrammatic language a sum over
a class of diagrams of all orders. The self-energy is
