Bhattacharjee J.K., Bhattacharyya S. Non-Linear Dynamics Near and Far from Equilibrium

Подождите немного. Документ загружается.

8.1 Description of the Turbulent State 233

and we can write Eq.(8.1.17) for an incompressible ﬂuid as,

∂E

∂t

=−ν



rω

(8.1.19)

As R →∞at ﬁxed L, one has ν →0 and hence a ﬁnite dissipation in this limit

implies that ω

has to blow up. Hence the derivatives of the velocity ﬁeld are going

to be ill deﬁned and in the turbulent regime, one expects the velocity ﬁeld to be non-

smooth. The solutions for the velocity ﬁeld are then thought of as distributions and

the notion of weak solutions of Navier-Stokes equation was accordingly introduced.

If φ

and ψ are smooth functions with compact support and ∂

=0, then v

(r)

will be called a weak solution of the Navier-Stokes equation if,



∂

ψd

rdt=0 (8.1.20)



rdt(v

∂

∇

)φ

=0 (8.1.21)

In D =3, weak solutions of the Navier-Stokes equation are known to exist.

We now return to the issue of energy balance in the case of turbulence and

including the external force



f , write Eq.(8.1.17) as

∂E

∂t

=−ν



r +



r (8.1.22)

If the total energy in turbulence is to remain constant in time, then the viscous

dissipation has to be balanced by the energy input



r.If is the rate at

which energy is injected and dissipated, then

 =ν



r =



r (8.1.23)

The feeding in of energy obviously occurs at the boundaries, i.e. at large length

scales L. The dissipation due to molecular viscosity occurs at short length scales

s where the viscous drag dominates the advective (nonlinear) term. The balance

leads to s ∼ν

3/4

/

1/4

. Between the scales L and s, the energy is transported by the

nonlinear term in the Navier-Stokes equation. If L

is the n

scale with l

=Lξ

ξ<1, and the velocity at that scale is v

, then the total energy is v

where

is the total volume occupied by the energy containing modes at the nth stage.

The typical turn over time for the eddy (mode) at the scale L

is τ =L

and

hence the rate 

at which energy crosses the n

stage is



/τ

(8.1.24)

In the Richardson-Kolmogorov scenario for this transfer process, 

is independent

of n and so is V

. Consequently,  =v

V/l at the scale l,or

=( ¯l)

1/3

(8.1.25)

234 8 Turbulence

where ¯ is the rate at which the energy density is dissipated. The scaling law in

Eq.(8.1.25) once again points towards a problem with the derivative at the small

scales.

The above discussion shows that between the outermost scale L and the inner-

most scale s is a range of scales l where the energy transfer is thought to occur

without any loss. This range is termed the inertial range and is the range in space

where the scaling law of Eq.(8.1.25) is valid. The ratio of the large to small scale

is given by

3/4



1/4

∝

3/4

(

)

1/4

3/4

(8.1.26)

For large R, the ratio of the two length scales is big and hence there will be a

signiﬁcant inertial range. The scale L serves as an infrared cutoff in the problem

and the scale s is an ultraviolet cutoff.

The picture of the velocity ﬁeld that is beginning to emerge is that of random

variable in time with non-smooth behaviour in space. Associated with the random-

ness is a distribution - one can think of averaging over time or one can envisage

an ensemble of systems differing in the initial conditions. The averages over time

and the ensemble averages will be equal due to ergodicity. In the inertial range,

the distribution function is universal. This is known through careful experiments,

where the velocity at a particular point of space is measured as a function of time

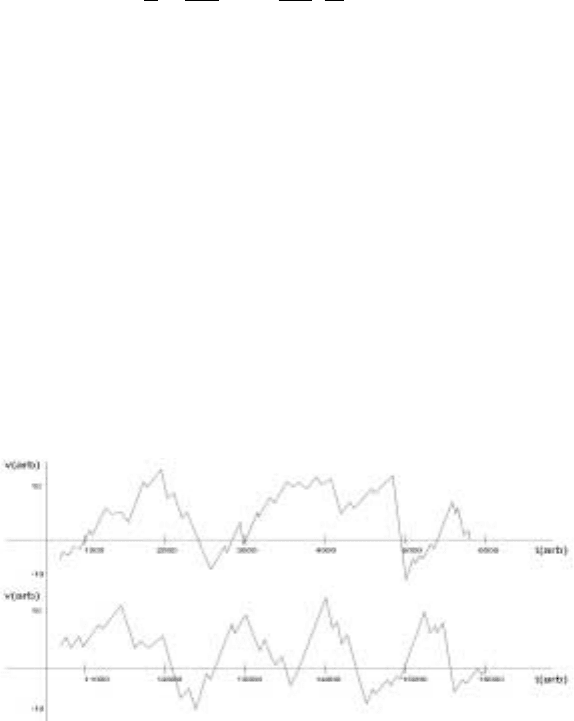
to generate a long time series. In Fig. 8.3, we show two parts of the time series over

the same interval of time. The time series from t =1000 to 5000 does not seem to

bear any correlation to the time series between t =11000 to 15000. However, if

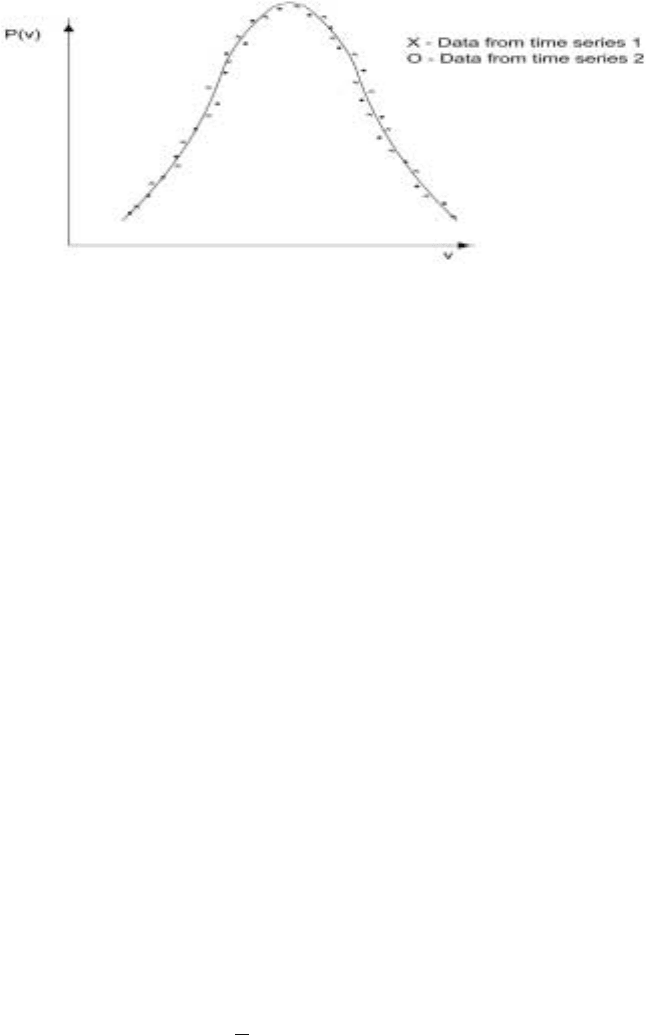
one makes a histogram about how many times a particular velocity is repeated then

one ﬁnds that the two histograms are almost identical, demonstrating while the

exact times series differ, the probability distribution remains the same (Fig. 8.4).

Figure 8.3. Time series for the velocity at a point

8.1 Description of the Turbulent State 235

Figure 8.4. Universality of the probability distribution

The probability distribution in the inertial range does not depend upon the way

energy is injected into the system or the way it is dissipated.

The central problem in the theory of turbulence is to start from the Navier-

Stokes equation and obtain the distribution function P(v(r,t)). If not the probabil-

ity distribution function, the moments of the velocity ﬁeld need to be calculated.

There is plausability argument for the existence of a distribution function. This is

a very crude way of looking at the problem but gives some feeling for what is in-

volved. We work at a given spatial point and discretize the Navier-Stokes equation

in time. The structure is

t+1

−v

=Av

−Bv

(8.1.27)

or after appropriate scalings

t+1

=ru

(1 −u

) (8.1.28)

The series generated from an initial condition u

remains bounded is r ≤4 Since

the velocity is bounded we require the u-variable in the discretized problem to be

bounded as well. We will analyze Eq.(8.1.28) for the limiting case of r =4. In this

case the substitution

=sin

(θ

) (8.1.29)

leads to

sin

(θ

t+1

) =4 sin

(2θ

) (8.1.30)

which means

t+1

= 2θ

if θ

≤π/4

t+1

= 2



−θ



if π/4 ≤θ

≤π/2 (8.1.31)

236 8 Turbulence

Calling θ

,wehave

t+1

= 2X

if 0 ≤X

≤1/2

t+1

= 2(1 −X

) if 1/2 ≤X

≤1 (8.1.32)

which is the well known tent-map. We write this as X

t+1

=f(X

) and if the

starting point is X

, the sequence that is generated is f(X

), f

(2)

), f

(3)

).....f

(N)

)..... where f

(N)

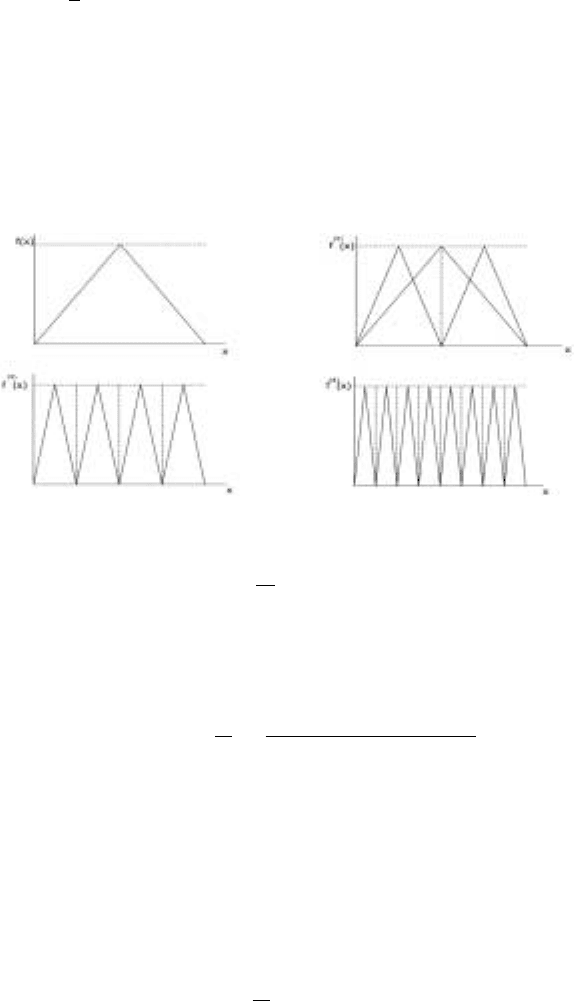
(X) =f (f (f (f....N times(X)))). The plot of

the successive iterates is shown in Fig. 8.5 It is clear from the above ﬁgure that if

Figure 8.5. Iterations of the tent map

the difference in initial conditions is

, the difference in the iterates after N-steps

is 1. This is the sensitive dependence on initial conditions, which is the signature

of chaos. The usual picture for chaotic evolution, which quantiﬁes the sensitiv-

ity to initial conditions, is the existence of a positive Lyapunov exponent λ. The

Lyapunov exponent is deﬁned as

λ = lim

N→∞,→0



(N)

+) −f

(N)

)





(8.1.33)

From the above discussion it should be clear that

λ =ln 2 (8.1.34)

for the above system.

A look at the iterates for the tent map shows that the sequence f

(N)

) ﬁlls

the unit interval completely with equal measure. We can deﬁne an invariant density

for the iterates as

ρ(X)= lim

N→∞



n=1

δ(X −f

(n)

)) (8.1.35)

8.2 Kolmogorov Phenomenology 237

the δ-function implying that we count one every time f

(N)

) =X. For the tent

map ρ(X)=const ant. The relation between X and V leads to a function for

V . The above argument makes it plausible why temporally the velocity ﬁeld is

going to show sensitive dependence on initial conditions which makes a statistical

description possible.

We summarize the basic features of the turbulent state as follows:

• i) It is the state of ﬂow as R →∞.

• ii) The velocity ﬁeld is random in time and hence a probabilistic description

with an ensemble consisting of systems with differing initial conditions is

appropriate.

• iii) The spatial dependence of the velocity ﬁeld is non-smooth in the sense that

derivatives may be singular.

• iv) There are two basic scales L and s. The large scale L is the scale at which

the system receives the energy from outside agencies and the small scale s is the

scale at which molecular diffusion becomes dominant. The ratio L/s =R

3/4

and hence for R →∞the scales are well separated.

• v) The intermediate scales L l s constitute the inertial range and in this

range universal features are obtained since things are independent of both the

feeding and dissipating mechanisms.

8.2 Kolmogorov Phenomenology

Kolmogorov phenomenology has to do with the short distance behaviour of the

correlation functions in the inertial range. We have already seen that assuming a

lossless energy transfer through the inertial range and the factthat energycontaining

eddies ﬁll the entire volume, one has the result that v

=¯

1/3

, where v

the velocity at the length scale l. The extraction of short distance behaviour of

correlation functions in the inertial range s l L, involves ﬁrst taking ν →0

(i.e.s →0) at ﬁxed positions of the ﬁelds and then taking a short distance limit with

L ﬁxed. For a n-point correlation function this means

lim

λ→0,ν→0

−ξ

u(λx

, t)u(λx

, t)....u(λx

,t)=ﬁnite (8.2.1)

Since in the inviscid limit, there are no other scales except the positions and L,

taking the last short distance limit is the same as L →∞. Kolmogorov assumed

that for Galilean invariant correlation functions i.e. correlation functions formed

from the differences v

(x)−v

(



0), the L →∞limit exists. Since they are to be

determined from  and x alone, the equal time correlation function

(r) ={[v(x) −v(



0)].

 (8.2.2)

238 8 Turbulence

follows from dimensional analysis and

(r) =C

(¯r)

n/3

(8.2.3)

for small r. In general since in the inviscid limit, there are three quantities ¯, r and

L available, we expect on dimensional grounds,

(r) =(¯r)

n/3

(r/L) (8.2.4)

Kolmogorov assumption is that as L →∞, F

(r/L) tends to C

which are universal

constants. For the energy spectrum, the above statements lead to the usual 5/3law.

This can be seen by writing the total energy as,

E =



rv(r)

=



kv(k)v(−k)



E(k)dk (8.2.5)

since v(r)

∼r

2/3

, the fourier transform v(k)v(−k)goes as k

−3−2/3

and from

Eq.(8.2.5) it follows that E(k) ∼k

−5/3

.Forn =3, one has the only exact result in

three dimensional turbulence, namely

(r) =−

¯r (8.2.6)

For n ≥4, derivatives from the Kolmogorov result begins to show up and the correct

phenomenology is

(r) =A

(¯r)

n/3

(

)

−n/3

(8.2.7)

as L →∞. Experiments show that ζ

<n/3. Consequently, the difference of S

(r)

from the Gaussian value ζ

=n/3 increases as one to shorter and shorter scales.

Hence the probability to have large velocity difference increases at short scales.

This is the phenomenon of intermittency.

The phenomenology is different in D =2 . The vorticity vector ω in D =3

obeys the equation of motion

d ω

+(v.



∇) ω −( ω.



∇)v =ν∇

ω +



∇×



f (8.2.8)

In D =2, ( ω.



∇)v =0 since ω happens to be in the z-direction and hence is not a

two dimensional vector. Consequently,

∂

ω +(v.



∇)ω =ν∇

ω +∇×f forcing term (8.2.9)

8.2 Kolmogorov Phenomenology 239

This means that in the absence of forcing



r is conserved in the inviscid

limit, i.e.

∂

∂t



r =−ν



(



∇ω)

r (8.2.10)

This quantity is known as the enstrophy. The fact that in the inviscid limit ω

cannot change means that it remains a constant as ν →0. The total energy is then

not dissipated at short scales. It is the enstrophy which gets dissipated and hence

there is an enstrophy ﬂux from larger to shorter scales. We have an enstrophy ﬂux

¯

given by,

lim

ν→0

ν(



∇ω)

=¯

(8.2.11)

In the inviscid limit, lim

ν→0

ν(



∇v)

=0 and hence the energy balance equation

in D =2is



=¯ (8.2.12)

So 

=¯t upto a constant and all energy injected into the system is transferred

to the ﬂuid. Steady state is not reached as a consequence of this. This energy is

transferred to the larger scales which is necessary to keep ∂



E(k)dk =0 while

∂



E(k)dk < 0 due to transfer of enstrophy to smaller scales. The picture in

D =2 is that there are two cascades - a forward enstrophy cascade and a backward

energy cascade. The enstrophy ﬂux ¯

has the dimensions of T

−3

and hence the

energy spectrum E(k) has the form,

E(k) =¯

2/3

−3

(8.2.13)

In D-dimensions, the relation between the velocity correlation function and E(k)

C(k)=v(k)v(−k)=

E(k)

D−1

(8.2.14)

and hence in D =2, C(k)∼k

−4

. This leads to

δv(r)

=



(2π)

C(k)(e



k.r

−1)

∼



(2π)



k.r

−1)

∼ r

ln r (8.2.15)

A generalization of the cascade argument given in Eq.(8.1.25), would imply

δv(r) ∼r which gives a smoother velocity ﬁeld than implied by Eq.(8.2.15). The

occurrence of logarithmic corrections is typical of D =2 and has been the subject

of a variety of analysis.

240 8 Turbulence

8.3 The Correlation Function

We begin with the two point function

(r) =



(x +r)−v

(x)][v

(x +r)−v

(x)]



(8.3.1)

Isotropy implies that C

cannot depend on any particular direction in space and

so C

has to be formed from

n, the unit vector in the direction of r. Thus,

(r) =A(r)δ

+B(r)n

(8.3.2)

Let us choose the coordinate axes along r. We call the velocity component along

r as v

and the transverse ones v

. Clearly,

= A +B

= A

= 0 (8.3.3)

We can write Eq.(8.3.1) as

(r) =2[v

(x)v

(x)−2v

(x +r)v

(x) (8.3.4)

Using the incompressibility conditions and differentiating w.r.t r

∂C

∂r

=0 (8.3.5)

Noting that

∂r

and that

we have by differentiating Eq.(8.3.2)

0 =

∂C

(r)

∂r



+B(4

−

) (8.3.6)

leading to



=0 (8.3.7)

8.3 The Correlation Function 241

It follows that



= 2(C

−C

)

or C

) (8.3.8)

In the inertial range, where C

∼r

2/3

(8.3.9)

For the dissipative range, the velocity difference is an analytic function of r and

we expect that for small r, v

∝r, which implies C

∼r

. consequently,

=2C

(8.3.10)

in the dissipative range. From Eq.(8.3.4)

v

(x +r)v

(x)=v

(x)v

(x)−

=v

(x)v

(x)−

A(r)δ

−

B(r)n

=v

(x)v

(x)+B(r)δ

−

B(r)n

+B(r)δ

−

B(r)n

(8.3.11)

If we write B(r) =ar

, then differentiating



∂v

(x

)

∂X

∂v

(x

)

∂X



=15a



∂v

(x

)

∂X

∂v

(x

)

∂X



=0 (8.3.12)

If we set r =



−



=0, then



∂v

∂X





= 15a

and



∂v

∂X

∂v

∂X



= 0 (8.3.13)

For the mean energy dissipation,

 =



∂v

∂X

∂v

∂X





=15aν (8.3.14)

242 8 Turbulence

leading to a =



15ν

. Consequently, in the dissipation range, we have



and C



(8.3.15)

We now turn to the three point function

ij k

(r) =[v

(x +r)−v

(x)][v

(x +r)−v

(x)]

×[v

(x +r)−v

(x)] (8.3.16)

First, we focus on v

(x)v

(x +r) and note that in the homogeneous,

isotropic situation this rank three tensor has to be constructed from δ

and n

the unit vector in the direction of r. The form is

v

(x)v

(x +r)=C(r)δ

+D(r)[δ

+δ

]

+F(r)n

(8.3.17)

The divergence free condition implies that

∂

∂r

v

(x)v

(x +r)=0 (8.3.18)

This derivative leads to two kinds of terms, those which are coefﬁcients of δ

and

those which are coefﬁcients of n

. The coefﬁcient of δ

leads to



C +D

=0 (8.3.19)

The coefﬁcient of n

in conjunction with Eq.(8.3.19) leads to

(3C +2D +F)]=0 (8.3.20)

Integrating

3C +2D +F =

constant

If we want a solution which remains ﬁnite at r =0, then

3C +2D +F =0 (8.3.21)

leading to

F =rC



−C (8.3.22)