Бездудный Г.М., Знаменский В.А., Коваленко Н.В. и др. Задачи по теории вероятностей. Часть 4
Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Г. М. Бездудный, В. А. Знаменский, Н. В. Коваленко,
В. Е. Ковальчук, А. И. Луценко, В. В Рындина
ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ
Часть 4
ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ФУНКЦИЙ СЛУЧАЙНЫХ
ВЕЛИЧИН, ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по решению задач по теории вероятностей
для студентов механико-математического факультета
Ростов-на-Дону
2003 г.
УДК 519.2
Г. М. Бездудный, В. А. Знаменский, Н. В Коваленко,
В. Е. Ковальчук, А. И. Луценко, В. В. Рындина
Задачи по теории вероятностей. Часть 4. Числовые характеристики функций
случайных величин, предельные теоремы теории вероятностей. Методические
указания к решению задач для студентов всех специальностей и всех форм
обучения механико-математического факультета РГУ.
Печатается по постановлению кафедры теории функций и функционального
анализа механико- математического факультета РГУ.
Протокол № 2 от 9 октября 2003 г.
Ответственный за выпуск – доктор физико-математических наук, профессор
Кондаков В. П.
Цель настоящей работы – помочь студентам в приобретении навыков по
решению задач по теории вероятностей. В начале каждого раздела приводится
необходимый теоретический материал, после чего подробно рассматривается
большое число типовых примеров.
© Коллектив авторов
Математическое ожидание и дисперсия
функций случайных величин
Математическое ожидание и дисперсия случайной величины η, связанной с
заданной одномерной случайной величиной ξ функциональной зависимостью
(
)
gη= ξ , определяются по формулам
() ()
M= gxdF x
+∞
ξ
−∞
η
∫
,
() () () () ( )
2
2
2
DMgx dF x g xdF x
+∞ +∞
ξξ
−∞ −∞
η= − η = − η
⎡⎤
⎣⎦
∫∫
M.
В случае, если ξ − дискретная случайная величина, принимающая значения
i
x
с вероятностями , , то указанные формулы принимают вид
i
p
1
i
i
p =
∑
(
)
M
ii
i
gx pη=
∑
,
() ( )
2
2
DM
ii
i
gxp
η
=−
∑
η
.
Если ξ − абсолютно непрерывная случайная величина с плотностью
вероятности
(
)
p
x , то
() ()
M gxpxdx
+∞
−∞
η=
∫
,
() () ( )
2
2
DMgxpxdx
+∞
−∞
η
=−
∫
η.
Если
(
)
12 n
,,,ξ= ξ ξ ξK − многомерная случайная величина, то для
M
η
,
D
η
в
дискретном случае имеют место формулы
(
)
(
)
11
1
111
M
nn
n
ini inni
i, ,i
gx , ,x p x , , xη= ξ = ξ =
∑
K
KK,
()
(
)
()
11
1
2
2
111
DM
nn
n
ini inni
i, ,i
gx,,x p x,, xη= ξ = ξ = − η
∑
K
KK
,
а в абсолютно непрерывном случае
()()
111
M
nn
g x , ,x p x , ,x dx dx
+∞ +∞
−∞ −∞
η=
∫∫
KK KK
n
,

()() (
2
2
111
DM
nnn
g x , ,x p x , ,x dx dx
+∞ +∞
−∞ −∞
η= − η
∫∫
KK KK
)
,
где
(
)
1 n
p
x, ,xK − плотность вероятности системы случайных величин
1 n
,,
ξ
ξK
.
Пример 1. Число элементов электронной машины, выходящих из строя за
некоторый промежуток времени, подчинено закону Пуассона с параметром a.
Длительность ремонта машины зависит от числа m вышедших из строя элементов
и определяется формулой
(
)
1
m
m
tT e
−γ
=− . Определить математическое ожидание
ущерба, причинённого простоем машины, если ущерб пропорционален квадрату
длительности ремонта:
.
2
mm
Skt=
Решение. В данной задаче встречаются три случайные величины: 1) ξ −
число элементов электронной машины, выходящих из строя за некоторый
промежуток времени (случайная величина ξ распределена по закону Пуассона с
параметром a); 2) η − длительность ремонта машины (случайная величина η
связана со случайной величиной ξ формулой
(
)
1Te
−γξ
η= − ); 3) ζ − величина
ущерба, причинённого простоем машины, связанная со случайной величиной η
формулой
.
2
kς= η
Случайная величина ζ есть функция от ξ следующего вида:
(
)
(
)
2
22
112kT e kT e e
2
−
γξ −γξ − γξ
ς= − = − + .
Имеем:
()
22
0
M12
!
m
mm a
m
a
kT e e e
m
∞
−γ − γ −
=
ς= − + ⋅ =
∑
() ()
22
00
11
2
!!
mm
aa a a
mm
kT e e e ae e ae
mm
∞∞
−−−γ −−γ
==
⎛⎞
=− ⋅+ ⋅
⎜⎟
⎝⎠
∑∑
=
(
)
(
)
2
11
2
12
ae ae
kT e e
−γ − γ
−− −−
⎛⎞
=− +
⎜⎟
⎝⎠
.

Пример 2. Случайная величина ξ имеет ряд распределения
−π/2
0
π/2
π
1/4 1/4 1/4 1/4
Найти математическое ожидание и дисперсию случайной величины .
cosη= ξ
Решение.
4
1
1
M0
42 2
ii
i
p cos x cos cos cos cos
=
⎛π π ⎞
⎛⎞
η= = − + + + π =
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
0
,
()
()
2
2222
11
DM M 0
42 2
cos cos cos cos
⎛π π ⎞
⎛⎞
η= η − η = − + + + π =
⎜⎟
⎜⎟
⎝⎠
⎝⎠
2
2
.
.
Пример 3. Пусть случайная величина τ − время безотказной работы детали
− распределена по показательному закону с параметром λ. Деталь заменяется в
любом случае по истечении времени T. Вычислить среднее время работы детали.
Решение. Время работы детали есть случайная величина
, где
()
gξ= τ
()
T,
TT
x, x
gx
,x
≤
⎧
=
⎨
>
⎩
Случайная величина τ имеет плотность вероятности
(
)
x
p
xe
−λ
=λ
, если 0
x
≥ , и
(
)
0px= , если 0
x
< . Поэтому
() ()
T
0T
M= T
xx
g x p x dx x e dx e dx
+∞ +∞
−λ −λ
−∞
ξ=λ+λ
∫∫∫
=
T
T
T
0
0
1
T
xxx
x
eedxe
+∞
−λ −λ −λ
⎛⎞
=λ − + − =
⎜⎟
⎜⎟
λλ
⎝⎠
∫
()
T
TT
0
11
TT1
x
ee e e
−λ −λ −λ −λ
−− + =−
λλ
T
.
Пример 4. Найти математическое ожидание и дисперсию модуля случайной
величины ξ, распределённой по нормальному закону с параметрами a и
2
σ
.
Решение. Плотность вероятности случайной величины ξ
()
()
2
2
2
1
2
x
a
px e
−
−
σ
=
σπ
.
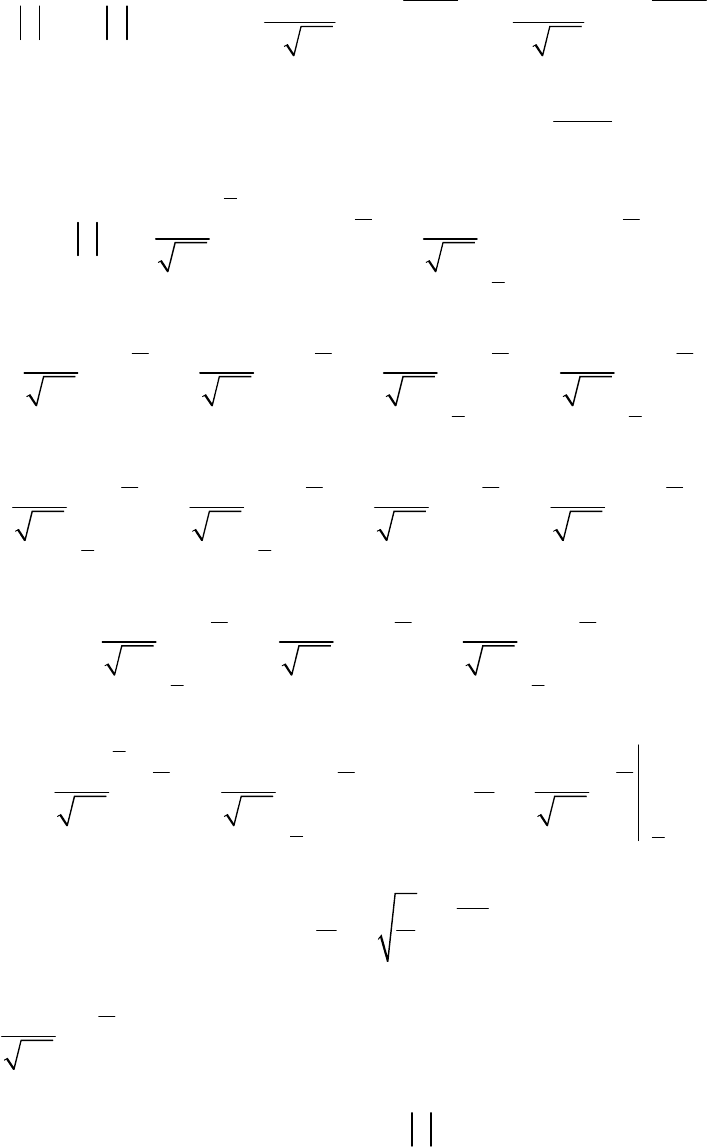
Поэтому
()
()
() ()
22
22
0
22
0
11
M
22
xa xa
x
p x dx xe dx xe dx
−−
+∞ +∞
−−
σσ
−∞ −∞
ξ= =− +
σπ σπ
∫∫∫
.
Сделав в каждом интеграле замену переменной
x
a
t
−
=
σ
, получим:
()
() ()
22
22
11
M
22
a
tt
a
atedt atedt
−
+∞
σ
−−
−∞
−
σ
ξ
=− +σ + +σ =
ππ
∫∫
222
00 00
222
22 22
ttt
aa
aa
edt tedt edt tedt
−−−
−∞ −∞
−−
σσ
σσ
=− − + + +
ππ ππ
∫∫ ∫∫
2
2
t
−
222
00
222
00
22 22
ttt
aa
aa
edt tedt edt tedt
+∞ +∞
−−−
−−
σσ
σσ
++ ++
ππ ππ
∫∫ ∫∫
2
2
t
−
=
22
00
22
0
22 2
22 2
tt
aa
a
edt tedt tedt
+∞
−−
−−
σσ
σσ
2
2
t
−
=
++
ππ π
∫∫ ∫
=
22
22
0
22 2
2
22 2
a
tt
a
a
aa
edt tedt a e
+∞
+∞
σ
−− −
−
−
σ
σ
σσ
⎛⎞
=+ =Φ−
⎜⎟
σ
ππ π
⎝⎠
∫∫
2
2
t
=
2
2
2
2
2
a
a
ae
−
σ
⎛⎞
=Φ + σ
⎜⎟
σπ
⎝⎠
,
где
()
2
2
0
1
2
t
z
ze
−
Φ=
π
∫
dt
− функция Лапласа.
Для нахождения дисперсии найдём
(
)
(
)
2
2
MM
ξ
=ξ
. Имеем:
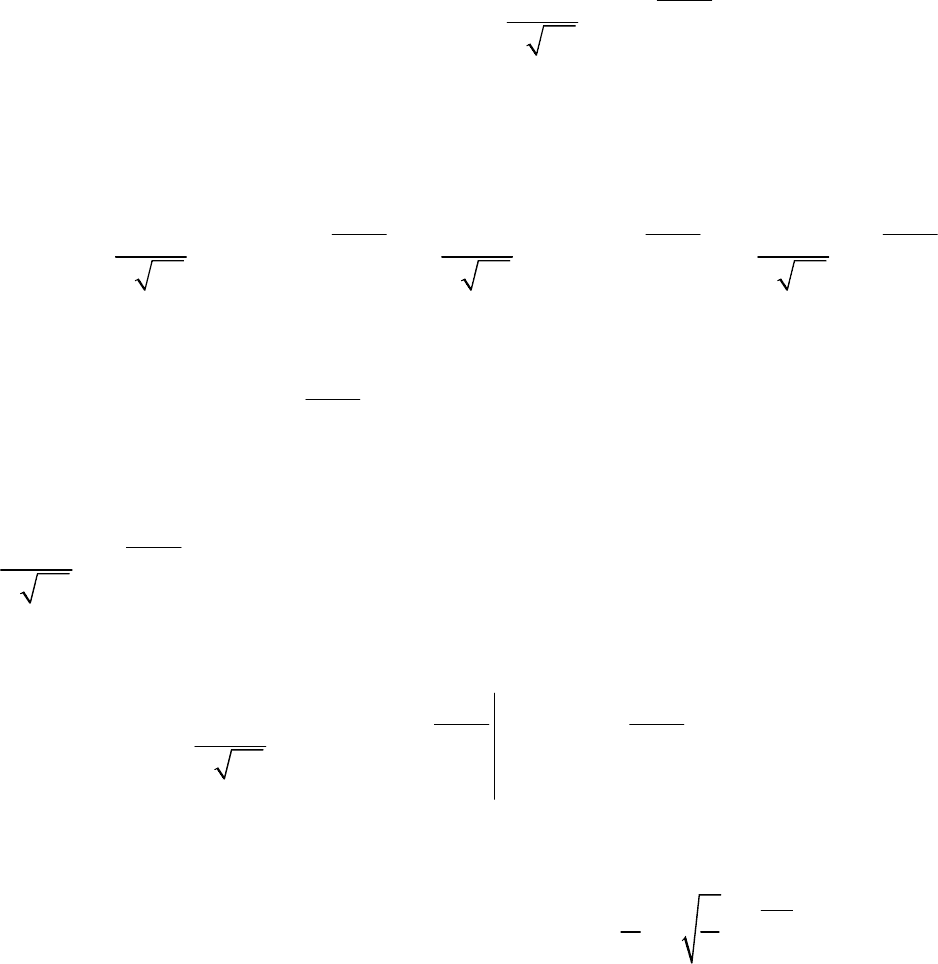
()
()
()
2
2
22 2
2
1
M
2
xa
x
p x dx x e dx
−
+∞ +∞
−
σ
−∞ −∞
ξ= =
σπ
∫∫
.
Заменив под знаком интеграла
2
x
на
()
(
)
2
x
aa−+
() ()
2
2
2
x
aaxaa
=
−+ −+
,
разобьём интеграл на три:
()
()
()
()
()
22
22
2
2
22
12
M
22
xa xa
a
x
ae dx xae dx
−−
+∞ +∞
−−
σσ
+
−∞ −∞
ξ= − + −
σπ σπ
∫∫
()
2
2
2
2
2
xa
a
ed
−
+∞
−
σ
−∞
σπ
∫
x
.
К первому интегралу применим формулу интегрирования по частям, положив
и
uxa=−
()
()
2
2
2
xa
dv x a e dx
−
−
σ
=−
, второй интеграл равен нулю (это становится
очевидным после замены
x
at
−
=
), а третье слагаемое равно , поскольку
2
a
()
2
2
2
1
1
2
xa
edx
−
+∞
−
σ
−∞
=
σπ
∫
как интеграл от плотности вероятности нормального закона
распределения. Поэтому
()
()
() ()
22
22
22 2 2
22
1
M
2
xa xa
22
x
ae e dx a a
+∞
−−
+∞
−−
σσ
−∞
−∞
⎛⎞
⎜⎟
ξ= −σ − +σ + =σ+
⎜⎟
σπ
⎜⎟
⎝⎠
∫
.
Тогда
()
()
2
2
2
222
2
2
DM M 2
a
a
aa e
−
σ
⎛⎞
⎛⎞
⎜⎟
ξ= ξ − ξ =σ + − Φ + σ
⎜⎟
σπ
⎜⎟
⎝⎠
⎝⎠
.
Пример 5. Найти математическое ожидание длины хорды, проведённой в
круге радиуса a перпендикулярно выбранному диаметру и пересекающей этот
диаметр в произвольной точке, все положения которой на выбранном диаметре
равновозможны.
Решение. Проведём через выбранный диаметр ось Ox, поместив начало
координат в центр круга.
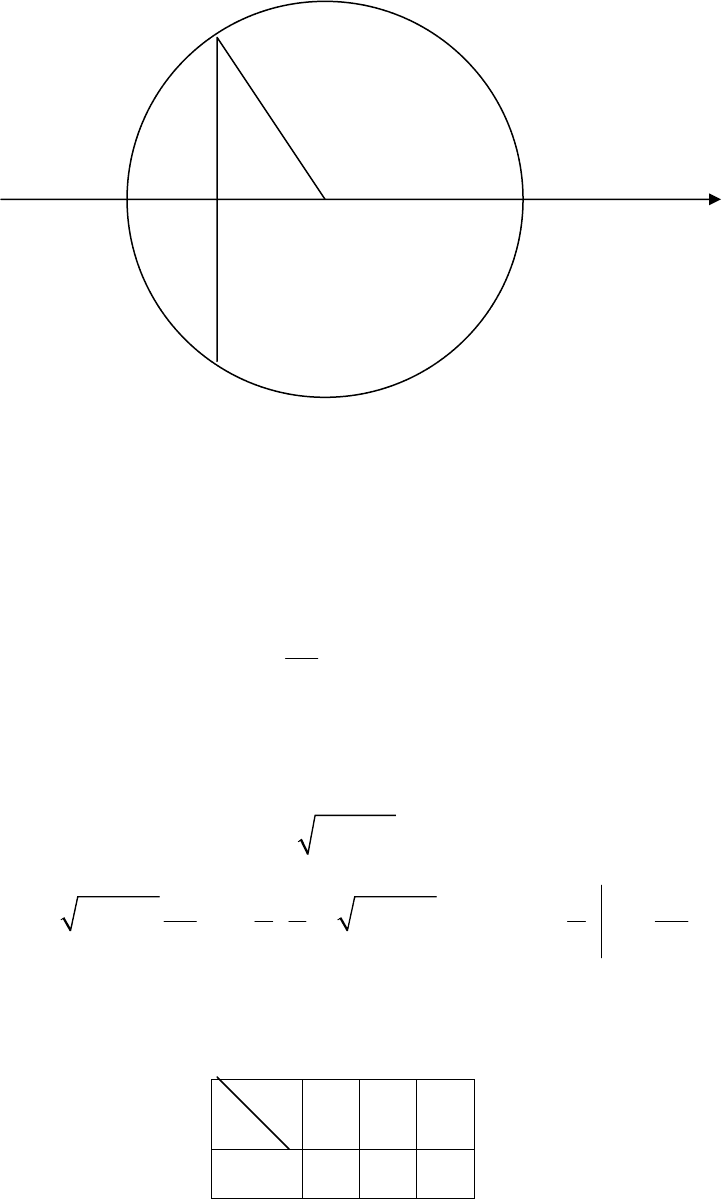
a
−a
ξ
O
x
Элементарными исходами в этой задаче являются точки отрезка [−a, a].
Пусть ξ − координата выбранной точки на отрезке [−a, a]. Случайная величина ξ
равномерно распределена на отрезке [−a, a], поэтому её плотность вероятности
()
[]
[]
1
2
0
,x a,a,
a
px
,x a,a.
⎧
∈−
⎪
=
⎨
⎪
∉−
⎩
Пусть η − длина хорды, проходящей через точку с координатой ξ
перпендикулярно оси Ox. Имеем:
2
2 a
2
η
=−ξ
, поэтому
22 22 2
111
M2
22
a
a
a
a
2
x
a
ax dx xaxaarcsin
aa a
−
−
π
⎡⎤
η= − = ⋅ − + =
⎢⎥
⎣⎦
∫
.
Пример 6.
Таблица распределения двумерной случайной величины имеет
вид:
ξ
η
0 1 2
0 1/4 1/4 0

1 1/4 0 1/4
Найти математическое ожидание и дисперсию случайной величины .
2
ς=ξ +ξη
Решение. Имеем:
()
()
2
11 1 1
MP0140020
44 4 4
iij i j
i,j
xxy x, yς= + ξ= η= =⋅+⋅+⋅+⋅+⋅+⋅=
∑
7
6
4
.
Для определения дисперсии найдём предварительно
(
)
(
)
(
)
24322 4322
MM 2 2 P
iijij i j
i,j
xxyxy x,yς= ξ+ξη+ξη = + + ξ= η= =
∑
11 1 13
0116004036
44 4 4
=⋅ +⋅+ ⋅+⋅+⋅+ ⋅ =
7
4
.
Теперь
()
()
2
2
37 49 99
DM M
41616
ς= ς − ς = − =
.
Пример 7.
Дважды бросается игральная кость. Пусть ξ − число очков,
выпавших при первом подбрасывании, η − число очков, выпавших при втором
подбрасывании. Найти математическое ожидание случайной величины
1
ς=
ξ
+η
.
Решение. Дискретная случайная величина (ξ, η) принимает значения (i, j),
. При этом
,1,2,,ij= K 6
()
1
P,
36
ijξ= η= =
. Поэтому
6
1
11
M
36
i,j
ij
=
ς
=⋅
+
∑
.
Для подсчёта Mζ составим таблицу возможных значений
.
ij+
i
j
1
2
3
4
5
6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
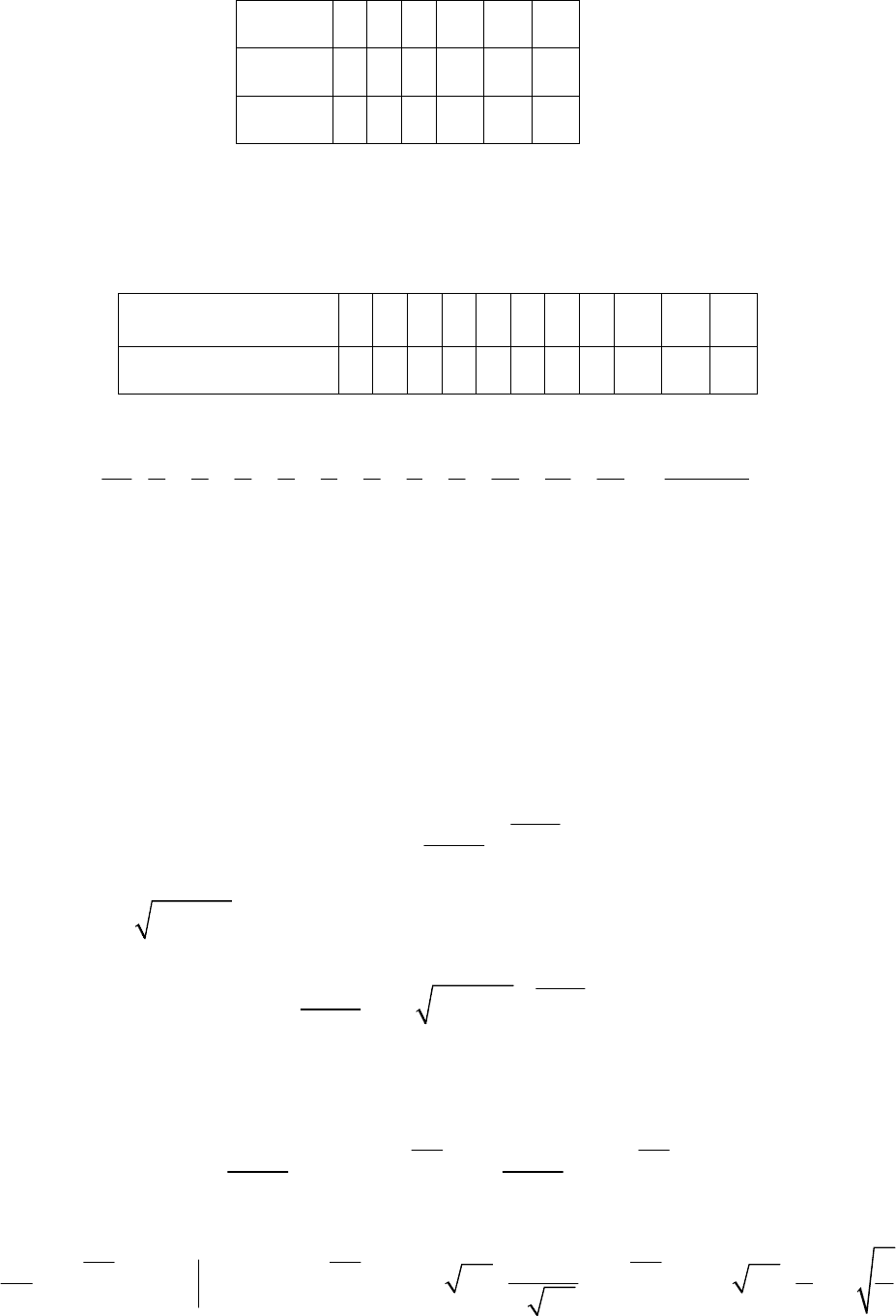
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 789101112
Из таблицы видно, что между значениями
ij
+
и числом слагаемых в Mζ
имеется следующее соответствие
Значение
ij+
2345678910 11 12
Число слагаемых 123456543 2 1
Поэтому
1 1 2 3 4 5 6 5 4 3 2 1 576677
M 0 578
36 2 3 4 5 6 7 8 9 10 11 12 997920
,
⎛⎞
ς= ++++++++ + + = ≈
⎜⎟
⎝⎠
.
Пример 8.
Случайная точка (ξ, η) распределена на плоскости по
нормальному закону с параметрами
M0
ξ
=
,
M0
η
=
, ,
2
Dξ=σ
2
D
η
=σ
,
. Найти математическое ожидание и дисперсию случайной величины
ζ, равной расстоянию от точки (ξ, η) до начала координат.
()
,cov ξη=0
Решение. Плотность вероятности двумерной случайной величины (ξ, η)
()
22
2
2
2
1
,
2
x
y
pxy e
+
−
σ
=
π
σ
.
Поскольку
2
ς= ξ +η
2
, то
22
2
22
2
2
1
M
2
xy
x
y e dxdy
+
+∞ +∞
−
σ
−∞ −∞
ς= +
πσ
∫∫
.
Переходя к полярной системе координат
x
rcos
=
ϕ
,
yrsin
=
ϕ
, получим:
22
22
2
2
22
22
00 0
12
M
22
rr
rdr re d r e dr
+∞ π +∞
−−
σσ
π
ς= ϕ= =
πσ πσ
∫∫ ∫
()
22 2
22 2
22
22 2
2
0
00
11
22
22
2
rr r
re e dr e dr
+∞ +∞
−− −
+∞
σσ σ
⎛⎞
1
π
⎜⎟
= ⋅ −σ +σ =σ π⋅ =σ π⋅ =σ
⎜⎟
σ
σπ
⎝⎠
∫∫
.
