Бездудный Г.М., Знаменский В.А., Коваленко Н.В. и др. Задачи по теории вероятностей. Часть 4
Подождите немного. Документ загружается.

22
22
2
22 3
22
22
00 0
12
M
22
rr
rdr r e d r e dr
+∞ π +∞
−−
σσ
π
ς
=ϕ=
πσ πσ
∫∫ ∫
=
() ()
22
22
222 2
222
2
0
0
0
1
22
rrr
re re dr e
+∞
+∞
−−−
+∞
σσ
⎛⎞
⎜⎟
=−σ+σ=−σ
⎜⎟
σ
⎝⎠
∫
2
2
2
2
σ
=σ
.
()
2
222
4
DM M 2
22
2
π
−π
ς= ς − ς = σ − σ = σ
.
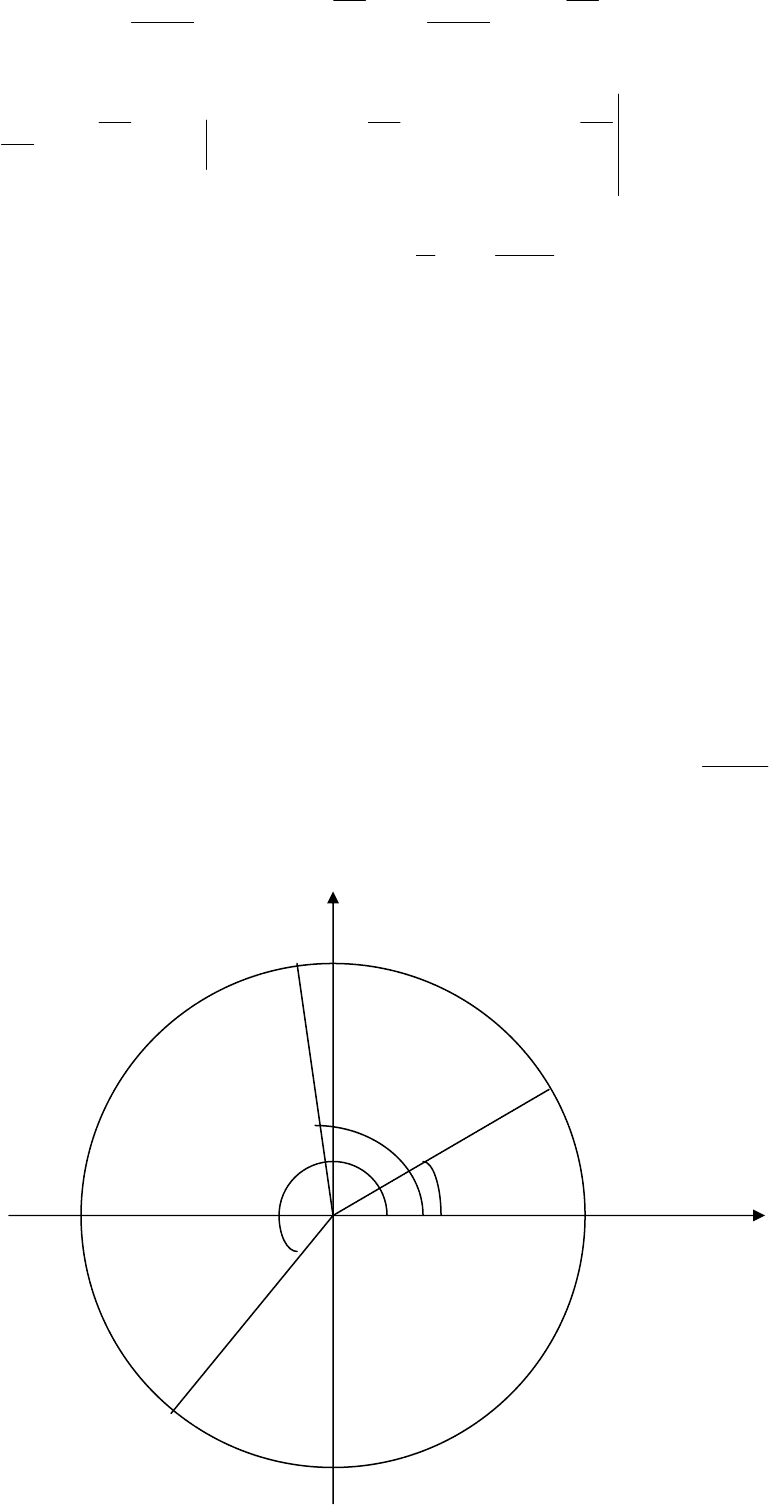
Пример 9. На окружности единичного радиуса наудачу ставятся три точки
A, B и C. Найти математическое ожидание площади треугольника ABC.
Решение. Рассмотрим декартову систему координат с началом в центре
круга. Пусть
,
1
ϕ
2
ϕ
, − углы между радиусами, идущими соответственно в
точки A, B, C и осью Ox, отсчитываемые от оси Ox против часовой стрелки.
3
ϕ
Координаты точек A, B, C равны
(
)
11
,cos sin
ϕ
ϕ
,
(
)
22
,cos sin
ϕ
ϕ
,
(
)
3
,cos sinϕϕ
3
. Величины углов
1
ϕ
,
2
ϕ
,
3
ϕ
являются случайными величинами,
равномерно распределёнными на отрезке
[
]
0, 2
π
и независимыми. Плотность
совместного распределения случайных величин
1
ϕ
,
2
ϕ
, равна
3
ϕ
()
3
1
2
π
, если
(
)
[
]
[
]
[
]
123
,, 0,2 0,2 0,2ϕϕ ϕ ∈ π× π× π
и нулю в противном случае.
A
C
O
1
ϕ
2
ϕ
3
ϕ
y
x

B
Ориентированная площадь S треугольника ABC выражается формулой
11
22
33
1
1
1
2
1
cos sin
Scossin
cos sin
ϕϕ
=ϕϕ
ϕϕ
.
Разлагая определитель по элементам последнего столбца, получим:
1
2
S =
[
(
)
(
)
23 32 13 31
cos sin cos sin cos sin cos sinϕ ϕ−ϕ ϕ− ϕϕ−ϕ ϕ+
(
)
12 2
cos sin cos sin+ϕϕ−ϕϕ
1
]
=
()()(
32 31 21
1
2
sin sin sin
⎡⎤
)
=
ϕ−ϕ − ϕ−ϕ + ϕ−ϕ
⎣⎦
.
Пусть случайная величина
ξ
−
площадь треугольника ABC. Между
ξ
и S
имеет место связь:
Sξ=
. Величина S неотрицательна, Если обход вершин
треугольника ABC совершается против часовой стрелки. Из этого следует, что
если
, то . Поскольку число различных перестановок
12
ϕ≤ϕ≤ϕ
3
0S ≥
1
ϕ
,
2
ϕ
,
3
ϕ
равно 3! и для любой из них
S
равен одному и тому же числу, то
()
()
222
123 1 2 3
3
000
1
MM ,,
2
SS ddd
πππ
ξ
== ϕϕϕ ϕϕϕ
π
∫∫∫
=
()
()()()
3
2
2
32 32 31 211
3
000
3!
22
dd sin sin sin d
ϕ
ϕ
π
⎡⎤
= ϕ ϕ ϕ −ϕ − ϕ −ϕ + ϕ −ϕ ϕ =
⎣⎦
π
∫∫∫
()
()()
()
()
3
2
3 2 32 32 3 2 2
3
00
3
1
2
d sin cos cos cos d
ϕ
π
⎡⎤
= ϕ ϕ ϕ −ϕ − ϕ −ϕ − ϕ + − ϕ ϕ =
⎣⎦
π
∫∫
()
() ()
33
2
33223223333
3
00 0
3
2
cos d cos d cos sin d
ϕϕ
π
⎡⎤
= ϕ− ϕ−ϕ ϕ− ϕ−ϕ ϕ+ϕ ϕ+ϕ− ϕ ϕ=
⎢⎥
π
⎢⎥
⎣⎦
∫∫ ∫
()
3
[]
2
3333333
3
0
3
2
2
sin cos sin d
π
= ϕ− ϕ+ϕ ϕ+ϕ− ϕ ϕ=
π
∫

()
[]
2
3333
3
0
3
23
2
sin cos d
π
=ϕ−ϕ+ϕϕ
π
∫
3
ϕ=
()
()
2
2
2
33 33
3
0
0
3
432 0
2
cos cos sin sin d
π
π
⎡⎤
=π+π−−ϕϕ+ϕϕ
⎢⎥
π
⎢⎥
⎣⎦
∫
=
()
()
2
3
33
2
2
2
=π=
π
π
.
Ковариационная матрица
Определение 1. Ковариацией случайных величин
ξ
,
η
называется число
(
)
(
)
,M MMcov
ξ
η= ξη− ξ⋅ η
.
Определение 2. Коэффициентом корреляции случайных величин
ξ
,
η
называется число
(
)
,
,
cov
ξη
ξ
η
ξ
η
ρ=
σ
⋅σ
,
где
D
ξ
σ= ξ
,
D
η
σ= η
.
Определение 3. Ковариационной матрицей системы случайных величин
(
)
12
,,,
n
ξξ ξK
называется квадратная матрица
,
,1
n
ij
ij
=
σ
, где
(
)
,
,
ij i j
covσ= ξξ
,
(
)
,
,D
ii i i i
covσ= ξξ=ξ
.
В дискретном случае имеет место формула
(
)
(
)
,
,P,M
km k m
km
cov x y x yξη= ξ= η= − ξ⋅ ηM
∑
.
В абсолютно непрерывном случае справедлива формула
() ()
,,cov xyp x y dxdy
+∞ +∞
ξη
−∞ −∞
ξη= − ξ⋅ η
∫∫
MM
.
Пример 1.
Бросаются две игральные кости. Пусть ξ − число очков на
первой кости, η − максимум из двух чисел очков. Найти математические
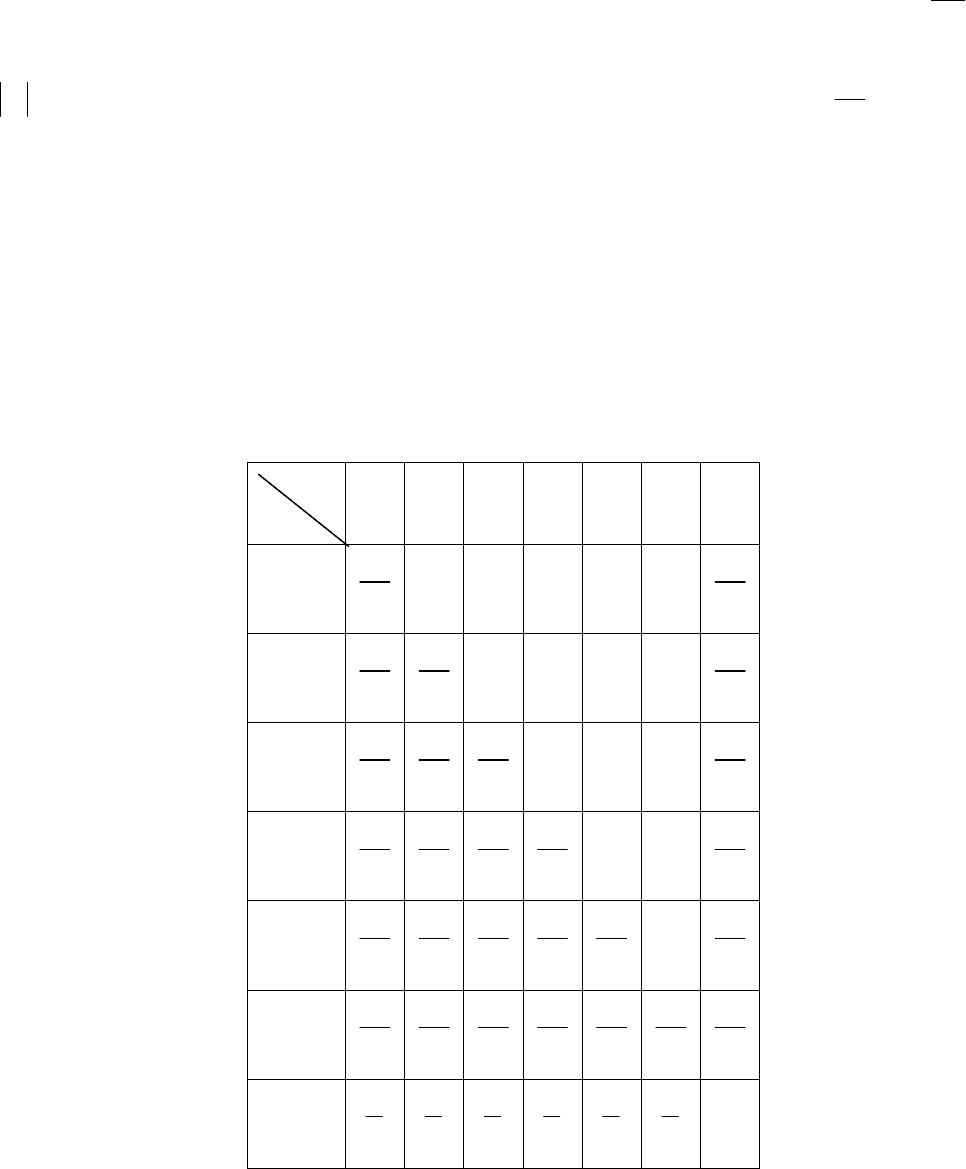
ожидания случайных величин ξ, η, ковариационную матрицу и коэффициент
корреляции.
Решение. В этой задаче элементарным исходом является вектор
(
)
,ij
, где i
− число очков на первой кости, j − число очков на второй кости. Пространство
элементарных событий состоит из равновозможных исходов:
(
)
{
}
,:, 1,6ij ijΩ= =
,
36Ω=
. Вероятность каждого элементарного события равна
1
36
. Имеем:
,
()
()
,ij iξ=
()
(
)
{
}
,ij maxijη=,
. Случайная величина
(
)
,ξη
− дискретная
двумерная случайная величина. Составим таблицу её распределения. Для этого
найдём
(
)
,
P,
ij
p
i=ξ=η=j
. Заметим, что
(
)
(
)
{
}
:,ij
ω
ξω= ηω= =∅
, если
;
ij>
(
)
(
)
{
}
(
)
(
)
(
)
{
}
:, ,1,,2,,,ijiiiωξ ω = ηω = = K i
, если
, и, наконец,
ij=
(
)
(
)
{
}
(
)
{
}
:, ,ijiωξ ω = ηω = = j
j
, если
i
<
. Поэтому
ξ
η
1 2 3 4 5 6
Σ
1
1
36
0
0
0
0
0
1
36
2
1
36
2
36
0
0
0
0
3
36
3
1
36
1
36
3
36
0
0
0
5
36
4
1
36
1
36
1
36
4
36
0
0
7
36
5
1
36
1
36
1
36
1
36
5
36
0
9
36
6
1
36
1
36
1
36
1
36
1
36
6
36
11
36
Σ
1
6
1
6
1
6
1
6
1
6
1
6
1
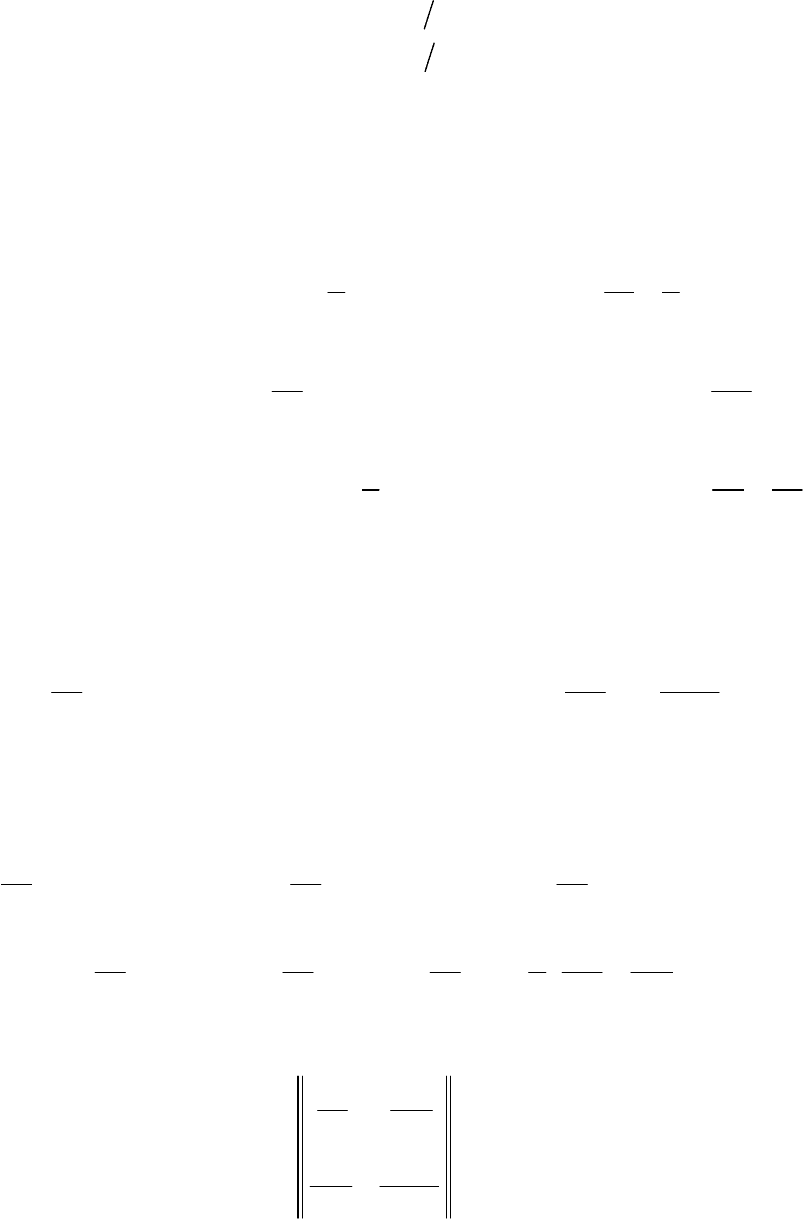
()
0, ,
P, 36,,
136, ,
ij
ijii
ij
>
⎧
⎪
j
ξ
=η= = =
⎨
⎪
<
⎩
и таблица распределения случайной величины
(
)
,
ξ
η
имеет приведённый выше
вид:
С помощью этой таблицы находим:
()()
6
1
12
M P 123456
66
kk
k
xx
=
17
2
ξ
= ξ= = +++++ = =
∑
;
()()
6
1
11
M P 132537495116
36 36
mm
m
yy
=
η= η= = + ⋅ + ⋅ + ⋅ + ⋅ + ⋅ =
∑
61
;
()()
()
6
2
2222222
11
1
14
D P M 123456
64
kk
k
xx
=
σ = ξ= ξ= − ξ = + + + + + − =
∑
935
12
;
()()
6
2
2
22
1
DP M
mm
m
yy
=
σ = η= η= − η =
∑
()
2
22 22 2
1 161 2555
132 53 74 95 116
36 36 1296
⎛⎞
=+⋅+⋅+⋅+⋅+⋅− =
⎜⎟
⎝⎠
;
() ( )
6
12 21
,1
,P,M
km k m
km
cov x y x y
=
σ=σ= ξη= ξ= η= − ξ⋅η=
∑
M
()
(
)
(
)
22
123
123456 2 3456 3 456
36 36 36
= +++++ + ++++ + +++ +
(
)
(
)
222
4567161
456 56 6
36 36 36 2 36 72
+ +++ ++ ⋅−⋅ =
105
.
Ковариационная матрица имеет вид:
35 105
12 72
105 2555
72 1296
.
Коэффициент корреляции
ξ
η
ρ
случайных величин ξ, η равен
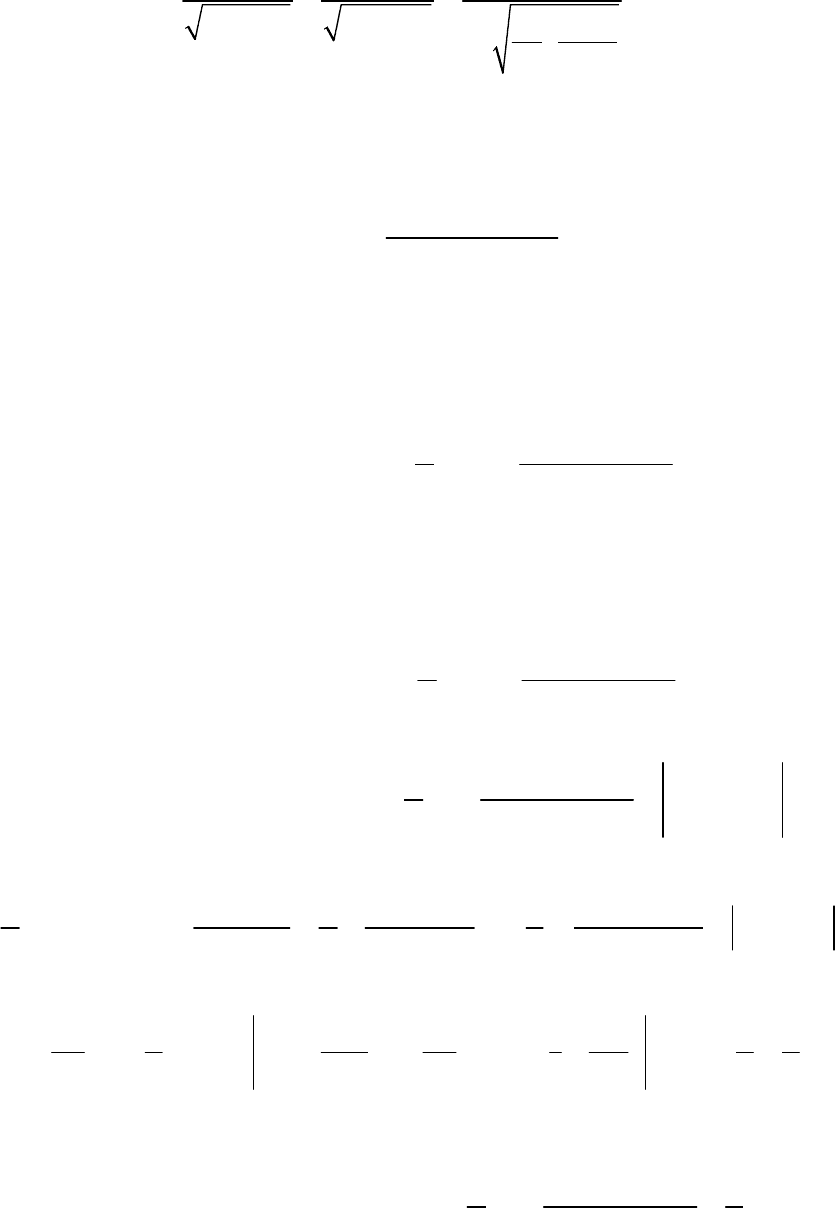
(
)
12
11 22
,
105
0,608
D D 35 2555
72
12 1296
cov
ξη
ξη
σ
ρ= = = ≈
ξ⋅ η σ ⋅σ
⋅
.
Пример 2.
Найти математические ожидания и ковариационную матрицу
системы случайных величин
(
)
,
ξ
η
, если плотность вероятности
()
()
3
22
2
,
1
pxy
xy
=
π++
.
Решение. Двумерная случайная величина
(
)
,
ξ
η
имеет абсолютно
непрерывное распределение.
()
()
3
22
2
M,
1
xdx
xp x y dxdy dy
xy
+∞ +∞ +∞ +∞
−∞ −∞ −∞ −∞
0
ξ
==
π
++
∫∫ ∫ ∫
=
,
так как внутренний интеграл берётся от нечётноё функции по симметричному
промежутку. Аналогично,
()
()
3
22
2
M,
1
ydy
yp x y dxdy dx
xy
+∞ +∞ +∞ +∞
−∞ −∞ −∞ −∞
0
η
==
π
++
∫∫ ∫ ∫
=
.
()
()
2
2
11
3
22
2
D,
1
xrcos
xdxdy
x p x y dxdy
yrsin
xy
+∞ +∞ +∞ +∞
−∞ −∞ −∞ −∞
=ϕ
σ=ξ= = = =
=ϕ
π
++
∫∫ ∫∫
()
(
)
()
22
22
3
2 2
33
22
00 0 0
1
22121
1
22
11
rd r
rdr cos
cos d d r t
rr
π+∞ π +∞
+
−ϕ
=ϕϕ⋅ = ϕ⋅ =+=
ππ
++
∫∫ ∫ ∫
=
2
32
01
1
11 11 11 1
22
22 2 2
2
t
cos dt
t
tt
π+
+∞
−
⎛⎞ ⎛⎞
=ϕ+ ϕ⋅ =⋅π⋅−+ =−=
⎜⎟ ⎜⎟
ππ
⎝⎠ ⎝⎠
∫
1
1
2
∞
.
Аналогично,
()
()
2
2
22
3
22
21
D,
2
1
ydxdy
y p x y dxdy
xy
+∞ +∞ +∞ +∞
−∞ −∞ −∞ −∞
σ=η= = =
π
++
∫∫ ∫∫
.

()
()
12 21
3
22
2
,0
1
ydy
xyp x y dxdy xdx
xy
+∞ +∞ +∞ +∞
−∞ −∞ −∞ −∞
σ=σ= = =
π
++
∫∫ ∫ ∫
.
Ковариационная матрица, таким образом, имеет вид:
12 0
012
.
Пример 3.
В круг
22 2
x
yR+≤
наудачу бросается точка. Рассматриваются
случайные величины: ξ − расстояние от точки до центра круга, η − расстояние от
точки до оси Oy. Найти математические ожидания и ковариационную матрицу
системы случайных величин
(
)
,
ξ
η
.
Решение. Пространство элементарных событий есть множество точек круга:
(
)
{
}
22 2
,:
x
yx y RΩ= + ≤
. Пусть X, Y − случайные координаты брошенной в круг
Ω точки. Двумерная случайная величина
(
)
,XY
имеет равномерное
распределение в круге Ω, т. е.,
()
()
()
2
,
1
,,
,
0, ,
XY
xy
R
pxy
,
x
y.
⎧
∈
Ω
⎪
π
=
⎨
⎪
∉
Ω
⎩
Случайные величины ξ и η есть следующие функции от случайных
координат X, Y:
22
XYξ= +
,
Y
η
=
.
Из этого следует, что
2
22 3
222
00
,
111
M2
33
R
xrcos
12
x
ydxdy drrdr R
yrsin
RRR
π
Ω
=ϕ
ξ= + ⋅ = = ϕ ⋅ = ⋅ π⋅ =
=ϕ
πππ
∫∫ ∫ ∫
R
,
2
3
22 2
00 0
11 11
M2
3
R
y dxdy sin d r rdr R sin d
RR R
ππ
Ω
η= ⋅ = ϕ ϕ ⋅ = ⋅ ⋅ ϕ ϕ=
ππ π
∫∫ ∫ ∫ ∫
0
24
33
R
R
cos
π
=− ϕ =
π
π
.

()
()
2
2
22 2 2
11
22
00
11
DM
9
R
4
x
ydxdy drrdrR
RR
π
Ω
σ=ξ= + ⋅ − ξ = ϕ ⋅ − =
ππ
∫∫ ∫ ∫
42
2
2
14
2
49 18
R
R
R
R
=⋅π⋅− =
π
.
()
2
2
2
222
22
22
00
11
DM
3
R
R
ydxdy sindrrdr
RR
π
Ω
⎛⎞
σ=η= ⋅ − η= ϕϕ ⋅ − =
⎜⎟
π
ππ
⎝⎠
∫∫ ∫ ∫
4
2
22
2
0
12 16
42
9
Rcos R
d
π
−ϕ
=ϕ−=
π
π
∫
22
2
22
216 116
42 4
99
RR
R
π
⎛⎞
⋅− =−
⎜⎟
π
ππ
⎝⎠
.
2
22 2
12 21
22
00
11
MM
33
R
24
R
yx ydxdy sind rrdr R
RR
π
Ω
σ=σ= + − ξ⋅ η= ϕϕ ⋅ − ⋅ =
π
ππ
∫∫ ∫ ∫
422
2
0
188
22
4929
22
9
R
RR RR
sin d
R
π
=⋅⋅ ϕϕ−=⋅−=
π
ππ
π
∫
π
.
Таким образом, ковариационная матрица имеет вид:
22
2
2
2
18 9
116
94
9
RR
R
R
π
⎛⎞
−
⎜⎟
π
π
⎝⎠
.
Локальная и интегральная теоремы Муавра-Лапласа
Рассматриваются повторные независимые испытания, или испытания по
схеме Бернулли. Вероятность появления некоторого случайного события в
единичном испытании равна p. Обозначим: событие
A
k
– “в серии из n испытаний
случайное событие произойдёт ровно k раз” и событие
B
– “число k наступлений
случайного события будет находиться в пределах от m
1
до m
2
”. Вероятности этих
событий определяются по формулам
P
n
(
)
k
A
kknk
n
Cpq
−
=
,
P
n
(
)
B
2
1
m
kknk
n
km
Cpq
−
=
=
∑
.
Для большого числа повторных независимых испытаний n при вычислении
вероятностей событий
и
по этим формулам возникают значительные, а
порой и непреодолимые, арифметические затруднения. Преодолеть их позволяют
локальная и интегральная теоремы Муавра-Лапласа, которые используют тот
факт, что функция
k
A
B
()
2
2
1
2
x
x
e
−
ϕ=
π
после некоторых линейных преобразований
хорошо аппроксимирует биномиальное распределение.
Локальная теорема. Если вероятность p появления случайного события в
единичном испытании удовлетворяет неравенству
0p 1
<
<
, то для k таких, что
()
(
)
23
knp onpq−=
будет справедливо приближённое равенство:
P
n
(
)
k
A
()
1
x
npq
≈ϕ
,
где
knp
x
npq
−
=
.
Интегральная теорема.
Если вероятность
p
появления случайного события в
единичном испытании удовлетворяет неравенству
0p 1
<
<
, то будет справедливо
приближённое равенство:
P
n
(
)
B
(
)
(
)
ba
≈
Φ−Φ
,
где
1
mnp
a
npq
−
=
,
2
mnp
b
npq
−
=
,
()
2
2
0
1
2
z
x
x
edz
−
Φ=
π
∫
−
функция Лапласа. Функция
(
)
x
Φ
нечётная, т.е.,
(
)
(
)
x
xΦ− =−Φ
, и для значений аргумента
x
, больших пяти,
принимают
(
)
05
x
,Φ=
.
Точность аппроксимации биномиального распределения оценивается
величиной
22
p
q
npq
+
. Отсюда видно, что чем больше
n
, тем приближённые
равенства будут точнее. Практически теоремы Муавра-Лапласа дают хорошую

аппроксимацию уже при .
9npq ≥
Пример 1. Некоторое случайное событие в каждом из
повторных
независимых испытаний происходит с вероятностью
432n =
025p,
=
. Найти вероятность
того, что это событие произойдёт:
а
) 108 раз;
б
) 111 раз;
в
) 120 раз. Чему равна
вероятность того, что число наступлений случайного события будет находиться в
пределах:
а
) от 108 до 117;
б
) от117 до 126;
в
) от 126 до135?
Решение
. Первая часть задачи требует применения локальной теоремы, т.е.,
вычисления вероятности
P
n
(
)
k
A
. Здесь
432 0 25 108np ,
=
⋅=
, и
81npq =
9npq
=
.
Вычисляем
knp
x
npq
−
=
для значений
1
108
k
=
,
2
111
k
=
, . Получаем:
3
120
k =
1
0
x
=
,
2
1
0 333
3
x
,=≈
,
3
4
1333
3
x
,=≈
. По таблицам определяем значения функции
(
)
x
ϕ
:
(
)
0 0 3989,ϕ=
,
(
)
0 333 0 3786,,ϕ=
,
(
)
1333 01640,,
ϕ
=
. Согласно локальной теореме
Муавра-Лапласа, получаем:
а
)
P
n
(
)
1
A
k
1
0 3989 0 0443
9
,,≈⋅ =
;
б
)
P
n
()
2
A
k
1
0 3786 0 0421
9
,,≈⋅ =
;
в
)
P
n
()
3
A
k
1
0 1640 0 0182
9
,,≈⋅ =
Однако при
имеем отклонение
3
120k =
12knp
−
=
, в то время как
()
23
4327
npq ,≈
. Сравнение этих величин приводит к выводу, что величина
третьего результата 0,0182 может значительно отличаться от значения
вероятности
P
.
n
()
3
A
k
Вторая часть задачи требует применения интегральной теоремы.
а
) Здесь
1
108
m
=
и
2
117
m
=
. Значит,
108 108
0
9
a
−
=
=
,
117 108
1
9
b
−
==
. По
таблицам определяем значения функции Лапласа
(
)
a
Φ
и и применяем
()
bΦ
