Бездудный Г.М., Знаменский В.А., Коваленко Н.В. и др. Задачи по теории вероятностей. Часть 4

Подождите немного. Документ загружается.

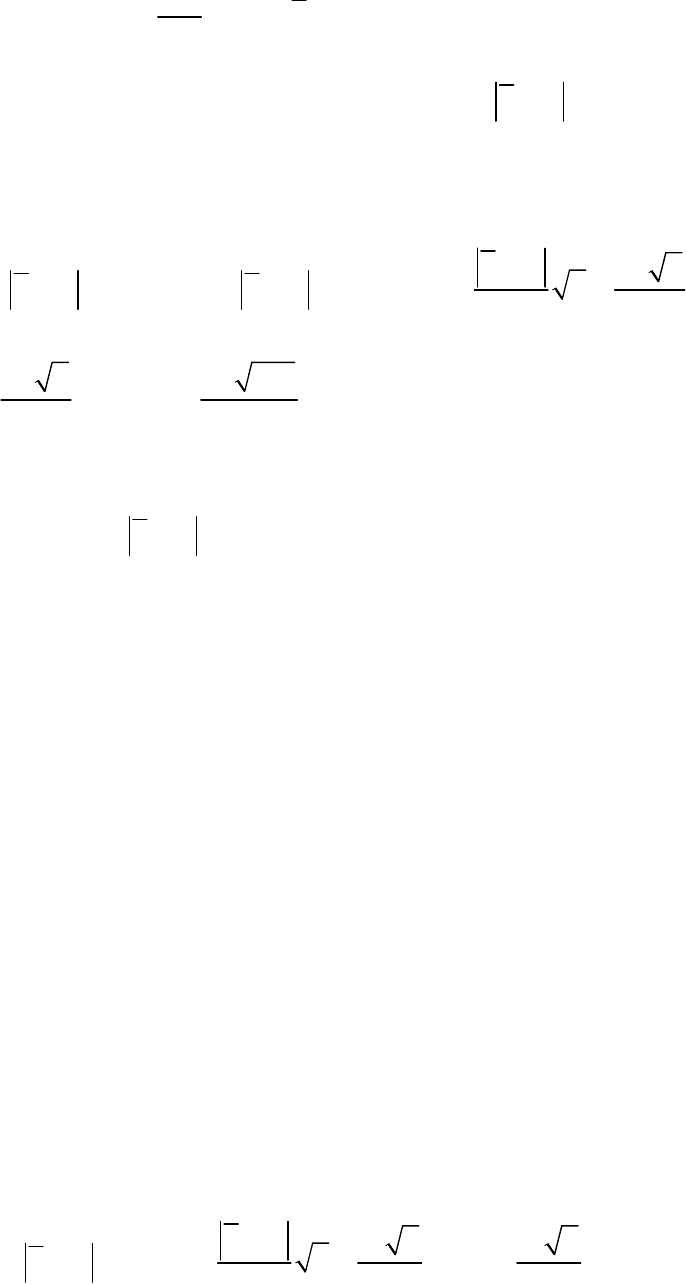
Если обозначить

900

=ξ

∑

, то для ответа на вопрос задачи нужно

оценить вероятность случайного события

{

}

12m,ξ− ≥

. Переходя к

противоположному событию и рассуждая, как и в предыдущем примере,

получаем:

()()

P121P121P

m, m, n

⎛⎞

ξ−

ξ− ≥ = − ξ− < = − < ≈

⎜⎟

σσ

⎝⎠

()

12 12 900

12 12 12 45 120499997 0000006

,n ,

,,,

⎛⎞ ⎛ ⎞

≈−Φ =−Φ =−Φ =−⋅ =

⎜⎟ ⎜ ⎟

⎝⎠ ⎝ ⎠

Так как получившаяся вероятность ничтожно мала, то можно сказать, что

случайное событие

{

}

12m,ξ− ≥

−

практически невозможное. Значит, такое

отклонение среднего веса призывников объяснить случайностью нельзя и следует

констатировать, что обследованный контингент призывников имеет в среднем

больший вес, чем

Пример 4. Производится выборочное обследование партии

электролампочек для определения средней продолжительности их горения. Каков

должен быть объём выборки, чтобы с уверенностью, не меньшей 0,9876,

утверждать, что средняя продолжительность горения лампочки по всей партии

отличается от средней, полученной в результате эксперимента, не более чем на 10

часов, если среднее квадратическое отклонение продолжительности горения

лампочки равно 80 часов?

Решение

. Эта задача является в некотором смысле обратной задаче примера

2. Поэтому используем обозначения и полученные неравенства этого примера. По

условию задачи, для должно быть справедливо:

nn≥

()

10 10

P 10 P 2 0 9876

⎛⎞

ξ−

⎛⎞

ξ− ≤ = ≤ ≈ Φ ≥

⎜⎟

σσ σ

⎝⎠

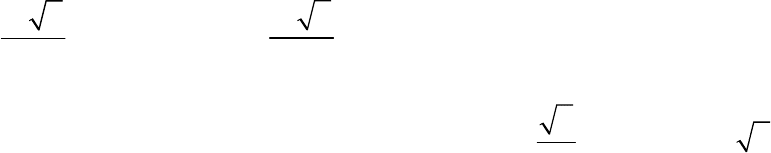
Следовательно, искомое число можно определить, решив неравенство

2 0 9876

⎛⎞

Φ≥

⎜⎟

⎝⎠

, или

(

0 4938

−

≥Φ

)

. По таблицам значений функции

Лапласа находим

(

)

0 4938 2 5

−

Φ=

. Значит,

,≥

, или

n ≥

, откуда

400n ≥

Литература.

1) Гнеденко Б. В. Курс теории вероятностей.

2) Ширяев А. Н. Вероятность.

3) Свешников А. А. и др. Сборник задач по теории вероятностей,

математической статистике и теории случайных функций.