Бейли Н. Математика в биологии и медицине

Подождите немного. Документ загружается.

ЧИСЛОВАЯ ТАКСОНОМИЯ 1Q1

Коэффициенты

корреляции

Коэффициенты

корреляции уже давно используются для изме-

рения

степени связи

между

двумя признаками. Обычно их при-

меняют к непрерывным переменным (или, во всяком случае,

дискретным переменным, характеризующимся некоторой упо-

рядоченностью).

Лучше

других

известен коэффициент корреляции

смешанных моментов, который легко использовать для измерения

сходства

между

двумя О. Т. Е. следующим образом. Допустим,

что все элементы основной матрицы п X t являются непрерывными

переменными. Тогда для j-ж таксономической единицы мы имеем

п измерений, обозначаемых х

, i = 1, . . ., п. Пусть среднее

из

этих величин равно х . Аналогично для к-ш таксономической

единицы имеются измерения x

k, £ = 1, . . . п со средним х^.

Наблюдаемый коэффициент корреляции смешанных моментов

между

этими двумя группами измерений равен

Oft =

'"'

——

•

(7-6)

ц=1

lJ 3

i=i

lk h

-I

Этот коэффициент изменяется от —1 в

случае

полной отрица-

тельной корреляции до +1 в

случае

полной положительной корре-

ляции.

Определить точный его смысл часто бывает трудно, однако

ясно,

что это определенный численный показатель ассоциации. Если

допустить, что рассматриваемые случайные величины характери-

зуются двумерным нормальным распределением, то можно при-

менить статистические критерии значимости и установить, напри-

мер, является ли значимым отличие данного коэффициента от нуля

или различие

двух

коэффициентов

друг

от

друга.

К сожалению,

для распределений, отличных от двумерного нормального, такая

проверка пока невозможна.

Если отдельные переменные получены в

результате

измерений

самого различного характера, то в этом

случае

нельзя предполо-

жить

даже

приближенно, что некоторая совокупность случайных

величин ХЦ (С варьированием по индексу г) имеет какое-либо

закономерное распределение, не говоря уже о нормальном.

Неко-

торого улучшения можно добиться путем нормировки элементов

по

рядам. Это означает, что все величины в данном

ряду

измеряют-

ся

относительно их среднего значения и делятся на их среднее

квадратическое отклонение. Полученные таким образом новые

величины, скажем Zjj, имеют нулевое среднее значение и единичное

среднее квадратическое отклонение. Следовательно, в этом

случае

все п величин в любом столбце имеют нулевое математическое

162

ГЛАВА

ожидание

единичное среднее квадратическое отклонение. Хотя,

вообще говоря, нормировка желательна, так как при этом мате-

риал становится более однородным,

во

многих

случаях,

когда

речь идет о фенетических соотношениях, она не

дает

ничего сущест-

венно

нового.

Показатели расстояния

Еще один способ установления степени

сходства

двух

таксоно-

мических единиц состоит

использовании некоторого показателя

«расстояния»

между

ними. Поясним это понятие, рассмотрев для

простоты случай, когда имеется всего три признака (т.

е. п =

3).

Пусть измерения показали, что эти признаки характеризуются

значениями

х^, x

j и x

для /-й О. Т.

Е. и

x^k,

h и х^

для к-ш

О. Т. Е. Тогда эти две таксономические единицы можно однознач-

но

изобразить

трехмерном пространстве точками (х^,

j, x

)

, x

h, x

расстояние

между

которыми

определяется

выражением

Ajft =

(х

—

)

—

)

(7.7)

Если бы признаков было бы только два,

то

каждую таксономи-

ческую единицу можно было бы представить точкой на двумерном

графике.

общем

случае

число признаков

очень велико,

для

изображения таксона необходимо га-мерное пространство. Обоб-

щенное

выражение для расстояния

между

/-й

к-ж таксономи-

ческими единицами

этом пространстве имеет вид

А)п=1\{хц-х

(7.8)

Если значения

и x

для

всех

(т.

е.

для каждого признака)

точности совпадают,

то

расстояние

Д^

между

точками равно

нулю. Любое различие приводит

возрастанию этой величины,

потому интуитивно представляется вполне разумным рассмат-

ривать расстояние как показатель различия.

Определенные проблемы возникают при нормировке, посколь-

ку относительные веса различных признаков очень сильно зависят

от используемой шкалы. Один

из

возможных способов состоит

кодировании каждой случайной величины таким образом, чтобы

ее значения лежали

интервале от

до 1. Это всегда можно выпол-

нить

путем соответствующих математических преобразований.

Если,

например,

изменяется от

до оо, то

у =

х/(а -\- х) (где

а —

некоторая произвольная положительная постоянная) изменяется

от

до

Но если мы изменим шкалу таким образом, что наиболь-

шее наблюдаемое значение не

будет

превосходить единицы, то при

рассмотрении новых таксономических единиц

более высокими

ЧИСЛОВАЯ ТАКСОНОМИЯ ^g 3

максимальными

значениями х всегда

будет

существовать опас-

ность того, что значительную часть данных потребуется пере-

кодировать заново. Другой метод состоит в нормировке данных

по

рядам матрицы, как это было описано при рассмотрении

коэф-

фициентов

корреляции. В этом

случае

все признаки имеют одно

то же математическое ожидание и одно и то же среднее квадра-

тическое отклонение, равные соответственно нулю и единице, что

придает им значительно большую взаимную эквивалентность.

При

добавлении новой О. Т. Е. возникает еще одна проблема

теоретического характера, поскольку первоначально определен-

ные

средние значения и средние квадратические отклонения

всех

рядов при этом изменятся и все элементы матрицы придется

нормировать заново. Однако введение только одной-двух новых

таксономических единиц должно потребовать лишь ничтожных

изменений

и на практике ими можно

будет

пренебречь. Так,

на

основе первоначальной нормировки необходимо пересчитывать

данные только по новым таксономическим единицам.

Если

мы решаем оперировать с нормированными измерениями

j, то введенную ранее формулу (7.8) для расстояния нужно заме-

нить

формулой

АЬ=Д'(2о--^)

. (7.9)

Величина Aj

зависит не только от самих результатов измерений

Zij, но и от числа сравниваемых признаков п. Лишь в одном слу-

чае, когда сравнения

между

всеми парами таксономических единиц

основаны

на одном и том же значении п, это не имеет существен-

ного значения. Для облегчения сравнения в тех

случаях,

когда

используются различные значения п, лучше вычислять средний

квадрат расстояния

^~- (7.10),

точки зрения числовой таксономии показатели таксономиче-

ского расстояния (7.9) и

(7.10)

являются простейшими и, по-види-

мому, наиболее удобными. В частных случаях используются

некоторые

другие

показатели расстояния или связанные с ними

коэффициенты

(например, коэффициент расового

сходства

Карла

Пирсона),

однако вряд ли есть необходимость рассматривать

их здесь. В частности, для диагностики широко используется

обобщенный

показатель

расстояния

Махаланобиса

. Однако

для рассматриваемых здесь проблем числовой таксономии этот

коэффициент

не подходит, так как мы не учитываем колебаний

данного признака внутри одной таксономической единицы.

164

ГЛАВА

Если в каком-либо частном

случае

все признаки имеют одина-

ковый характер, т. е. все они непрерывны или дискретны, то мож-

но

выбрать метод измерения

сходства,

который

будет

приемлем

в общем случае. Но если одни признаки дискретны, а

другие

непрерывны, то возникают известные трудности (аналогичная

проблема встречается при использовании математических методов

для диагностики; см. гл. 11). В этом

случае

можно либо приме-

нять

для

всех

признаков коэффициенты корреляции (или показа-

тели расстояния), рассматривая непрерывные случайные вели-

чины обычным способом, а дискретные — описывая числовыми

значениями

0 и 1, либо произвольным образом разбить непрерыв-

ные случайные величины на дихотомические классы и для каждого

признака

использовать коэффициент ассоциации. С теоретической

точки зрения ни один из этих методов нельзя считать удовлетво-

рительным, однако на современном начальном этапе развития

числовой таксономии они

могут

иметь известную практическую

ценность. По мере того как точность числовой таксономии

будет

повышаться, потребуются, конечно, более точные методы анализа.

Для тех, кто знаком с выполнением статистических исследо-

ваний,

ясно,

что любой процесс получения оценок связан с такими

понятиями,

как значимость и точность. Можно, например,

поин-

тересоваться, значимо ли различие

двух

коэффициентов

сходства.

До сих пор в этом отношении сделано очень мало. Нелегко разра-

ботать математическую модель, которая бы учитывала совместное

влияние таксономических единиц и признаков на результаты

измерений и удовлетворительно описывала бы изменения, ожи-

даемые при повторном выборочном измерении. Кроме того, нас

интересует не сравнение каких-либо

двух

коэффициентов

сходства,

а оценка всей t X ^-матрицы коэффициентов (см. разд. 7.5). Эта

задача теории выборочного метода весьма сложна, и она может

приобрести исключительно важное значение при более широком

использовании методов числовой таксономии. Мы описали здесь

применение нормировки применительно к некоторым распределе-

ниям,

хотя это выполнялось в довольно эвристической манере,

а не на основе какой-либо точно сформулированной модели повтор-

ного выбора. Поэтому на данном этапе описанные здесь методы

необходимо рассматривать как полезное средство, точность кото-

рого неизвестна.

7.5. ПОСТРОЕНИЕ ФЕНОНОВ

Итак,

у нас уже имеется матрица t X t, составленная из вычис-

ленных коэффициентов

сходства,

и мы можем перейти к третьему

этапу процесса, описанного в разд. 7.3. В дальнейшем мы

будем

.считать, что все коэффициенты нормированы и заключены

между

ЧИСЛОВАЯ

ТАКСОНОМИЯ

165

О и 1. Как уже указывалось в предыдущем разделе, таким обра-

зом обычно нормируют коэффициенты ассоциации, связанные

с дискретными случайными величинами; коэффициенты корреля-

ции

лежат

между

—1 и +1, а показатели расстояния

могут

лежать

совсем в

другом

интервале. Если для

всех

случайных величин

используются коэффициенты одного типа, то никаких затрудне-

ний

не возникает, поскольку их можно сравнивать

друг

с другом,

какая

бы шкала ни была выбрана. Если же в одном и том же

исследовании используются коэффициенты разного типа, то их

можно сделать сравнимыми, произведя некоторые простые пре-

образования. Это очевидный, хотя и важный пункт.

помощью матрицы

сходства

мы хотим разбить операбельные

таксономические единицы на такие группы, чтобы единицы одной

группы обладали близким сходством, а

между

единицами, при-

надлежащими к разным группам,

сходство

было значительно

меньшим. Проиллюстрируем эту операцию на искусственном

примере с небольшим числом таксономических единиц. Допустим,

что у нас есть 10 О. Т. Е., для которых нижняя половина 10 X 10-

матрицы коэффициентов имеет вид, показанный в табл. 3, где

для простоты все коэффициенты округлены до 0,1.

Таблица

Типичная

ЮхЮ-матрица

коэффициентов

сходства

для 10 О. Т. Е.

Но:

1,0

0,9

0,6

0,5

0,9

0,6

0,5

0,8

0,6

1,0

0,5

0,6

0,8

0,6

0,5

0,9

0,6

1,0

0,5

0,6

0,8

0,5

0,6

0,7

1,0

0,5

0,9

0,5

0,6

1,0

0,6

0,5

0,9

0,6

,6 1,0

,5 0,6 1,0

9 10

Номер

О. Т. Е.

Минимальное значение коэффициента

сходства

в табл. 3 равно

0,5. Произвольно примем 0,5 и 0,6 за относительно слабое, а 0,7,

0,8 и 0,9 (особенно последние два значения) за относительно

сильное сходство. Изучение табл. 3 показывает, что О. Т. Е.

№ 1 имеет близкое

сходство

с О. Т. Е. № 2, 5 и 9, причем послед-

166

ГЛАВА

ние

три

имеют очень близкое

сходство

друг

другом; связь любой

из

этих четырех

О. Т. Е. с

любой

из

остальных шести значительно

слабее. Таким образом,

О. Т. Е. № 1, 2, 5 и 9

выглядят

как

особая

группа. Кроме того,

следует

выделить

О. Т. Е. № 4 и 8. Они

сильно

связаны

друг

другом,

но не

связаны

какими-либо

дру-

гими

О. Т. Е.

Наконец, оставшиеся

О. Т. Е. № 3, 6, 7 и 10

также

можно собрать

группу,

хотя

этом

случае

два

«внутренних»

коэффициента

сходства

равны всего

0,7.

Разобьем

эти 10 О. Т. Е.

на

три

названные группы. Тогда матрица примет

вид,

показан-

ный

табл.

Таблица

Перегруппированный вариант матрицы

коэффициентов

сходства,

изображенной

табл.

1,0

0,9

0,8

0,6

0,5

1,0

0,8

0,9

0,5

0,6

0,5

1,0

0,9

0,6

0,5

0,6

0,5

1,0

0,6

0,5

0,6

1,0

0,6

0,5

1,0

0,9

1,0

Номер

О. Т. Е.

Структура исходной матрицы теперь довольно ясна. Правда,

нам

точно

не

известна статистическая значимость этих

трех

групп,

которые можно рассматривать

как три

фенона, определенных

на

основе первоначальных данных

признаках

при

70%-ном

уровне значимости,

но, во

всяком случае,

у нас

теперь есть основа

для числовой таксономической классификации.

сожалению, описанный выше процесс распределения опера-

бельных таксономических единиц

по

группам, основанный

на ви-

зуальном изучении матрицы коэффициентов

сходства,

крайне

субъективен

и его

трудно выполнить, когда число таксономиче-

ских единиц больше

10.

Сокэл

Снит

[59]

описывают метод,

который

по

существу

аналогичен данному

и в

котором интервал

значений

коэффициентов

сходства

указывается

помощью квадра-

тов, имеющих различную

густоту

штриховки.

этом

случае

ЧИСЛОВАЯ ТАКСОНОМИЯ

167

группировку произвести несколько легче, однако

при

большом

числе таксономических единиц возникают

те же

проблемы. Ясно,

что необходим некоторый более систематический метод анализа,

особенно

в тех

случаях, когда требуется выявить иерархию групп.

Один

из

методов, используемый Снитом

другими исследова-

телями, состоит

том,

что

вначале образуют группу

из

наиболее

близких

друг

другу

таксономических единиц

(двух

или

более),

для которых коэффициент сходства имеет некоторое произвольно

выбранное высокое значение. Затем последовательно рассматри-

вают

ряд

более низких уровней сходства;

те О. Т. Е.,

которые

обнаруживают рассматриваемую

или

более высокую степень

сходства

каким-либо представителем предыдущей группы, вклю-

чают

в эту

группу,

остальные выделяют

отдельную группу.

Такая

методика может привести

росту первоначальной группы

или

появлению новых групп.

По

очевидным причинам этот метод

называется односвязным (single-linkage). Допустим,

что

имеется

ряд коэффициентов сходства 0,99;

0,98;

0,97 и т. д. и

распределе-

ние

групп оказалось таким,

как

показано

табл.

Смысл этой

таблицы состоит

том,

что

только

О. Т. Е. № 1 и 2

имеют

коэф-

фициент

сходства

не

менее 0,99;

О. Т. Е. № 3

имеет коэффициент

сходства

не

менее

0,98 с О. Т. Е. № 1 и 2, а О. Т. Е. № 4 и 5

имеют такой

же

коэффициент сходства

друг

другом, но ни

одним

из

представителей первой группы. При уровне

0,97

обе эти группы

смыкаются

появляется новая группа, содержащая

О. Т. Е.

№

6 и 7.

Применять этот метод нетрудно, однако

он

может при-

вести

образованию разбросанных групп,

которых крайние

члены относительно мало похожи

друг

на

друга.

Таблица

Образование

групп

односвязным

методом

Коэффициент

сходства

0,99

0,98

0,97

0,90

Группы таксономиче-

ских

з,

единиц

5, 6,

Другим критерием, который использовал Сёренсен

эколо-

гических исследованиях, служит правило «полной связи» («com-

plete-linkage»

rule). Оно состоит

том,

что

данную группу может

168

ГЛАВА

быть помещена только такая новая таксономическая единица,

у которой коэффициент сходства с любым членом группы дости-

гает требуемого уровня. Естественно, что это довольно строгое

условие приводит к образованию довольно компактных, четко

определенных групп.

Более приемлемым

следует

считать критерий «средней связи»

(«average-linkage»

criterion), предложенный Сокэлом и Миченером.

Как

следует

из названия, этот критерий допуска новой таксоно-

мической единицы в группу основан на ее среднем сходстве со

всеми представителями этой группы. Существует несколько спо-

собов формирования групп в этом случае. Один из простейших

(и

наиболее легкий для программирования при использовании

ЭВМ) — так называемый взвешенный парно-групповой метод

(«weighted

pair-group» method). Согласно этому методу, первую

группу образуют из

двух

наиболее близких таксономических

единиц.

Затем матрицу коэффициентов преобразуют путем замены

первой пары таксономических единиц соответствующей группой.

После этого вычисляют новые коэффициенты сходства, показы-

вающие связь между данной группой и любой другой таксономи-

ческой единицей. Так, если О. Т. Е. № 1 и 2 образуют первую

группу (обозначим ее, скажем, № 1'), то коэффициент сходства

для О. Т. Е. № 3 и группы № 1' равен среднему значению

коэффи-

циентов сходства для О. Т. Е. № 3 и 1 и О. Т. Е. № 3 и 2. Изу-

чение новой матрицы с целью нахождения максимального

коэф-

фициента сходства показывает, какая таксономическая единица

должна объединяться с группой № 1' или какие две таксономи-

ческие единицы должны образовать следующую новую группу.

Этот процесс можно выполнять просто и однозначно шаг за шагом,

образуя на каждом этапе вычислений только одну новую группу

или включая одну новую таксономическую единицу в существую-

щую группу. Разумеется, существует ряд технических деталей,

связанных, в частности, с тем, используются ли коэффициенты

ассоциации,

коэффициенты корреляции или же показатели рас-

стояния.

В нашу задачу не входит обсуждение всех этих вопросов,

поскольку нас интересуют лишь основные принципы числовой

таксономии. Более полно этот вопрос рассматривается в упоми-

навшейся ранее книге Сокэла и Снита [59], особенно в приложе-

нии

А.З, где дается несколько конкретных примеров.

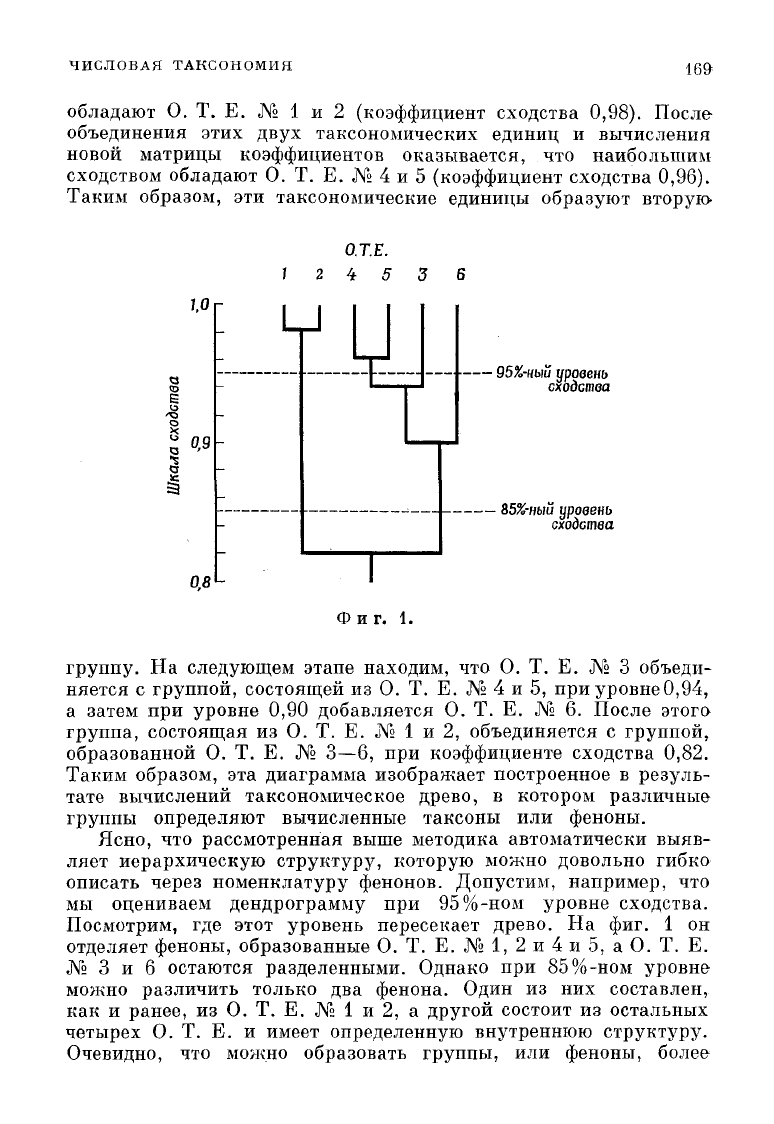
Результаты таких вычислений удобно представлять схемати-

чески в виде дендрограммы, показывающей, при каком уровне

сходства образуются различные группы. Допустим, что приме-

нение

взвешенного парно-группового метода к шести таксономи-

ческим единицам дало результат, изображенный на фиг. 1, где

порядок таксономических единиц выбран лишь для графического

удобства. Из этой схемы можно видеть, что наибольшим сходством

ЧИСЛОВАЯ ТАКСОНОМИЯ

16»

обладают О. Т. Е. № 1 и 2 (коэффициент

сходства

0,98).

После-

объединения этих

двух

таксономических единиц и вычисления

новой

матрицы коэффициентов оказывается, что наибольшим

сходством обладают О. Т. Е. № 4 и 5 (коэффициент

сходства

0,96).

Таким

образом, эти таксономические единицы образуют вторую.

—

95%-ный уровень

сходства

—

85%-ный уровень

сходства

Фиг.

группу.

На следующем этапе находим, что О. Т. Е. № 3 объеди-

няется

с группой, состоящей из О. Т. Е. № 4 и 5, при уровне0,94,

а затем при уровне 0,90 добавляется О. Т. Е. № 6. После этога

группа, состоящая из О. Т. Е. № 1 и 2, объединяется с группой,

образованной

О. Т. Е. № 3—6, при коэффициенте

сходства

0,82.

Таким

образом, эта диаграмма изображает построенное в резуль-

тате

вычислений таксономическое древо, в котором различные

группы определяют вычисленные таксоны или феноны.

Ясно,

что рассмотренная выше методика автоматически выяв-

ляет иерархическую

структуру,

которую можно довольно гибко

описать через номенклатуру фенонов. Допустим, например, что

мы оцениваем дендрограмму при 95%-ном уровне

сходства.

Посмотрим,

где этот уровень пересекает древо. На фиг. 1 он

отделяет феноны, образованные О. Т. Е. № 1, 2 и 4 и 5, а О. Т. Е.

№

3 и 6 остаются разделенными. Однако при 85% -ном уровне

можно различить только два фенона. Один из них составлен,

как

и ранее, из О. Т. Е. № 1 и 2, а

другой

состоит из остальных

четырех О. Т. Е. и имеет определенную внутреннюю

структуру.

Очевидно, что можно образовать группы, или феноны, более

170

ГЛАВА

высокого

«ранга»,

чем те, которые получены при первой группи-

ровке основных таксономических единиц. По своему общему

виду таксономическое древо, полученное вычислительными

методами, и древо, полученное преимущественно на основании

биологических соображений, несомненно, близки. Вопрос о надеж-

ности

таких построений имеет исключительно большое значение,

в следующем разделе мы обсудим с этой точки зрения некоторые

результаты, полученные к настоящему времени с помощью методов

числовой таксономии.

7.6. ПРИЛОЖЕНИЯ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

В настоящее время

ведутся

большие споры о ценности и потен-

циальных возможностях числовой таксономии для биологической

классификации,

и, безусловно, еще слишком рано делать какие-

либо окончательные выводы. Тем не менее уже сейчас

следует

дать числовому

подходу

некоторую предварительную оценку,

особенно

если учесть, что он создает для таксономии значительно

более точную научную основу, чем та, которая существовала

до настоящего времени.

Прежде всего нужно сказать, что методы, описанные в послед-

них

трех

разделах, уже были применены для классификации

самых разнообразных организмов. Например, в зоологии такие

авторы, как Миченер, Рольф и Сокэл (более детальные ссылки

на

эти работы приводятся в книге Сокэла и Снита [59], а также

других

работах, упоминаемых далее), исследовали 97 видов

пчел комплекса

Hoplitis,

объединяющего четыре рода семейства

Megachilidae. Вычисленные коэффициенты

сходства

и полученные

дендрограммы хорошо согласуются с системой, предлагаемой

ортодоксальной таксономией. Кроме того, были получены новые

данные о тонкой

структуре

иерархии таксонов и о положении

системе некоторых отклоняющихся видов. Выполненное Роль-

фом

числовое исследование 48 видов комаров рода

Aed.es

также

привело к системе, весьма похожей на ту, которая явилась резуль-

татом

других

исследований этой группы. Аналогичным образом

Литтл, используя методы числовой таксономии, проанализировал

на

основе 36 признаков 103 вида губок рода

Cliona

и пришел

системе, хорошо согласующейся с современными таксономиче-

скР1ми

идеями.

В ботанике применение числовых методов также дало хорошее

совпадение с существующей системой, особенно в работе Мори-

сима и Ока по исследованию различных видов риса

(Oryza)

и в ра-

боте Сориа и Хейзера по исследованию рода

Solarium.

Значительную работу выполнили Снит и многие

другие

иссле-

дователи по применению числовых методов при классификации