Беспалов В.И. Системы и источники энергоснабжения

Подождите немного. Документ загружается.

ɡɨɜɚɧɢɹ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ ɜɨ ɜɪɟɦɟɧɢ ɢɥɢ ɦɟɠɞɭ ɨɬɞɟɥɶɧɵɦɢ

ɩɪɟɞɩɪɢɹɬɢɹɦɢ ɷɬɨɬ ɤɨɷɮɮɢɰɢɟɧɬ ɰɟɥɟɫɨɨɛɪɚɡɧɨ ɢɫɩɨɥɶɡɨɜɚɬɶ ɜ ɩɟɪ-

ɜɭɸ ɨɱɟɪɟɞɶ.

ȼ ɪɹɞɟ ɫɥɭɱɚɟɜ, ɧɚɩɪɢɦɟɪ, ɩɪɢ ɩɥɚɧɢɪɨɜɚɧɢɢ ɷɧɟɪɝɨɩɨɬɪɟɛɥɟɧɢɹ

ɧɚ ɩɪɟɞɩɪɢɹɬɢɢ, ɩɨ ɦɧɟɧɢɸ ɚɜɬɨɪɨɜ [1] ɫɭɦɦɚɪɧɨɟ ɤɨɥɢɱɟɫɬɜɨ ɩɨɬɪɟɛ-

ɥɟɧɧɵɯ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ, ɩɨɞɜɟɞɟɧɧɵɯ ɤ ɩɪɟɞɩɪɢɹɬɢɸ, ɦɨɠɧɨ

ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɪɚɡɜɟɪɧɭɬɨɦ ɜɢɞɟ, ɤɚɤ ɪɚɡɧɨɫɬɶ ɦɟɠɞɭ ɩɨɬɪɟɛɧɨɫɬɶɸ ɢ

ɜɧɭɬɪɟɧɧɢɦ (ɫɨɛɫɬɜɟɧɧɵɦ) ɩɪɨɢɡɜɨɞɫɬɜɨɦ

ɷɧɟɪɝɨɧɨɫɢɬɟɥɟɣ:

ioij i

noT i

BS BB BB

ªº

§·

«»

¨¸

«»

©¹

¬¼

'

¦¦

(1.3)

ɝɞɟ i

– ɜɢɞɵ ɩɨɛɨɱɧɵɯ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ, ɨɛɪɚɡɭɸɳɢɯɫɹ ɧɚ

ɩɪɟɞɩɪɢɹɬɢɢ

'1, 'im

;

oij

– ɩɨɬɪɟɛɧɨɫɬɶ ɩɪɨɰɟɫɫɚ j ɜ ɷɧɟɪɝɟɬɢɱɟɫɤɨɦ ɪɟɫɭɪɫɟ ɜɢɞɚ i, ɨɩɪɟɞɟ-

ɥɹɟɦɚɹ ɧɚ ɨɫɧɨɜɟ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɛɚɥɚɧɫɚ ɷɬɨɝɨ ɩɪɨɰɟɫɫɚ;

– ɤɨɥɢɱɟɫɬɜɨ ɢɫɩɨɥɶɡɨɜɚɧɧɵɯ ɜ ɩɪɨɰɟɫɫɟ j ɩɨɛɨɱɧɵɯ ɷɧɟɪɝɟɬɢɱɟ-

ɫɤɢɯ ɪɟɫɭɪɫɨɜ ɜɢɞɚ i

, ɜɡɚɦɟɧ ɪɟɫɭɪɫɚ ɜɢɞɚ i;

– ɜɧɭɬɪɟɧɧɟɟ (ɫɨɛɫɬɜɟɧɧɨɟ) ɩɪɨɢɡɜɨɞɫɬɜɨ i ɧɚ ɨɫɧɨɜɧɵɯ ɝɟɧɟɪɢɪɭɸ-

ɳɢɯ ɭɫɬɚɧɨɜɤɚɯ ɩɪɟɞɩɪɢɹɬɢɹ (ɜ ɨɬɥɢɱɢɟ ɨɬ ɭɬɢɥɢɡɚɰɢɨɧɧɵɯ ɭɫɬɚɧɨɜɨɤ);

ǻB

noT,i

– ɩɨɬɟɪɢ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɪɟɫɭɪɫɚ ɜɢɞɚ i ɜɨ ɜɧɭɬɪɢɡɚɜɨɞɫɤɢɯ

ɤɨɦɦɭɧɢɤɚɰɢɹɯ;

– ɤɨɷɮɮɢɰɢɟɧɬ ɩɨɥɟɡɧɨɝɨ ɞɟɣɫɬɜɢɹ ɩɪɨɰɟɫɫɚ j ɧɚ ɩɨɛɨɱɧɨɦ ɷɧɟɪɝɟ-

ɬɢɱɟɫɤɨɦ ɪɟɫɭɪɫɟ ɜɢɞɚ i

;

– ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɢɜɟɞɟɧɢɹ ɪɚɡɥɢɱɧɵɯ ɷɧɟɪɝɨɧɨɫɢɬɟɥɟɣ ɤ ɩɪɢɪɨɞɧɵɦ

ɷɧɟɪɝɟɬɢɱɟɫɤɢɦ ɪɟɫɭɪɫɚɦ, ɪɚɜɧɵɣ

, (1.4)

ɝɞɟ

– ɫɭɦɦɚɪɧɵɣ ɄɉȾ ɰɟɩɨɱɤɢ ɷɧɟɪɝɨɫɧɚɛɠɟɧɢɹ ɞɥɹ ɷɧɟɪɝɟɬɢɱɟɫɤɨ-

ɝɨ ɪɟɫɭɪɫɚ i.

ɉɨɞɫɬɚɜɥɹɹ ɜɵɪɚɠɟɧɢɟ (1.3) ɜ ɡɧɚɦɟɧɚɬɟɥɶ ɮɨɪɦɭɥɵ (1.2), ɦɨɠɧɨ

ɩɨɥɭɱɢɬɶ ɨɰɟɧɤɭ, ɯɚɪɚɤɬɟɪɢɡɭɸɳɭɸ ɷɧɟɪɝɟɬɢɱɟɫɤɭɸ ɷɮɮɟɤɬɢɜɧɨɫɬɶ

ɨɫɧɨɜɧɵɯ ɧɚɩɪɚɜɥɟɧɢɣ ɫɨɜɟɪɲɟɧɫɬɜɨɜɚɧɢɹ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɯɨɡɹɣɫɬɜɚ

ɩɪɨɦɵɲɥɟɧɧɨɝɨ ɩɪɟɞɩɪɢɹɬɢɹ. Ʉɚɤ ɜɢɞɧɨ ɢɡ ɷɬɢɯ ɮɨɪɦɭɥ, ɪɨɫɬ ɤɨɷɮɮɢ-

ɰɢɟɧɬɚ ɩɨɥɟɡɧɨɝɨ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɩɪɢɪɨɞɧɵɯ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ

ɦɨɠɟɬ ɛɵɬɶ ɨɛɟɫɩɟɱɟɧ ɡɚ ɫɱɟɬ:



ɉɨɜɵɲɟɧɢɹ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɩɨɛɨɱɧɵɯ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ (B

);



ɋɧɢɠɟɧɢɹ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɩɨɬɟɪɶ ɜɨ ɜɧɭɬɪɢɡɚɜɨɞɫɤɢɯ ɤɨɦɦɭɧɢ-

ɤɚɰɢɹɯ (ǻB

noT,i

);



ɉɨɜɵɲɟɧɢɹ ɄɉȾ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ ɜ ɤɨɧ-

ɤɪɟɬɧɵɯ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɯ ɩɪɨɰɟɫɫɚɯ (Ș

);



ɉɪɚɜɢɥɶɧɨɝɨ ɜɵɛɨɪɚ ɷɧɟɪɝɨɧɨɫɢɬɟɥɟɣ (S

);



ɉɪɚɜɢɥɶɧɨɝɨ ɜɵɛɨɪɚ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɯ ɩɪɨɰɟɫɫɨɜ ɢ ɢɯ ɪɟɠɢɦɨɜ

(ȼ

ɉɨɜɵɲɟɧɢɟ Ș

ɧɚ ɜɟɥɢɱɢɧɭ į ɡɚ ɫɱɟɬ ɪɟɚɥɢɡɚɰɢɢ ɧɚɡɜɚɧɧɵɯ ɜɵɲɟ

ɦɟɪɨɩɪɢɹɬɢɣ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɷɤɨɧɨɦɢɢ ɬɨɩɥɢɜɚ ɜ ɪɚɡɦɟɪɟ:

ij i ij

i=1 j=1

BkȘ

ǻB=B - ɬ

Ș (1+į)

¦¦

(1.5)

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɚɧɚɥɢɡ Ʉɉɂ ɩɨɡɜɨɥɹɟɬ ɧɟ ɬɨɥɶɤɨ ɨɰɟɧɢɬɶ ɷɮɮɟɤ-

ɬɢɜɧɨɫɬɶ ɷɧɟɪɝɨɢɫɩɨɥɶɡɨɜɚɧɢɹ ɧɚ ɩɪɨɦɵɲɥɟɧɧɨɦ ɩɪɟɞɩɪɢɹɬɢɢ, ɧɨ ɢ

ɜɵɹɜɢɬɶ ɨɛɴɟɤɬɵ, ɤɨɬɨɪɵɟ ɜ ɦɚɤɫɢɦɚɥɶɧɨɣ ɦɟɪɟ ɜɥɢɹɸɬ ɧɚ ɭɪɨɜɟɧɶ ɢɫ-

ɩɨɥɶɡɨɜɚɧɢɹ ɪɟɫɭɪɫɨɜ ɢ ɩɨɷɬɨɦɭ ɬɪɟɛɭɸɬ ɩɨɫɬɨɹɧɧɨɝɨ ɤɨɧɬɪɨɥɹ.

ɋɥɟɞɭɸɳɟɟ ɧɚɩɪɚɜɥɟɧɢɟ ɚɧɚɥɢɡɚ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɛɚɥɚɧɫɚ ɩɪɨ-

ɦɵɲɥɟɧɧɨɝɨ ɩɪɟɞɩɪɢɹɬɢɹ ɡɚɤɥɸɱɚɟɬɫɹ ɜ ɨɩɪɟɞɟɥɟɧɢɢ ɫɜɹɡɢ ɷɧɟɪɝɟɬɢɤɢ

ɫ ɨɫɧɨɜɧɵɦɢ ɩɨɤɚɡɚɬɟɥɹɦɢ ɯɨɡɹɣɫɬɜɟɧɧɨɣ ɞɟɹɬɟɥɶɧɨɫɬɢ

ɢ ɨɰɟɧɤɢ ɜɡɚ-

ɢɦɧɨɝɨ ɜɥɢɹɧɢɹ ɷɧɟɪɝɟɬɢɤɢ ɢ ɷɤɨɧɨɦɢɤɢ ɩɪɨɢɡɜɨɞɫɬɜɚ. ɗɬɨ ɧɚɩɪɚɜɥɟ-

ɧɢɟ ɚɧɚɥɢɡɚ ɩɪɟɞɭɫɦɚɬɪɢɜɚɟɬ ɪɚɫɱɟɬ ɨɛɨɛɳɟɧɧɵɯ ɷɧɟɪɝɨɷɤɨɧɨɦɢɱɟɫɤɢɯ

ɯɚɪɚɤɬɟɪɢɫɬɢɤ ɩɪɟɞɩɪɢɹɬɢɹ, ɢɡ ɤɨɬɨɪɵɯ ɧɚɢɛɨɥɟɟ ɜɚɠɧɵɦɢ ɹɜɥɹɸɬɫɹ:

Ž ɷɧɟɪɝɨ- ɢ ɷɥɟɤɬɪɨɜɨɨɪɭɠɟɧɧɨɫɬɶ ɬɪɭɞɚ;

Ž ɷɧɟɪɝɨ-, ɷɥɟɤɬɪɨ- ɢ ɬɟɩɥɨɟɦɤɨɫɬɶ ɩɪɨɞɭɤɰɢɢ;

Ž ɷɧɟɪɝɨ-, ɷɥɟɤɬɪɨ- ɢ ɬɟɩɥɨɨɫɧɚɳɟɧɧɨɫɬɶ ɨɫɧɨɜɧɵɯ ɩɪɨɢɡɜɨɞɫɬɜɟɧ-

ɧɵɯ ɮɨɧɞɨɜ;

Ž ɬɟɩɥɨɷɥɟɤɬɪɢɱɟɫɤɢɣ ɢ ɷɥɟɤɬɪɨɬɨɩɥɢɜɧɵɣ ɤɨɷɮɮɢɰɢɟɧɬɵ;

ɢ ɪɹɞ ɞɪɭɝɢɯ ɩɨɤɚɡɚɬɟɥɟɣ.

ɂɡɭɱɟɧɢɟ ɬɟɧɞɟɧɰɢɣ ɢɡɦɟɧɟɧɢɹ ɷɬɢɯ ɩɨɤɚɡɚɬɟɥɟɣ ɩɨɡɜɨɥɹɟɬ

ɜɫɤɪɵɬɶ ɨɫɧɨɜɧɵɟ ɡɚɤɨɧɨɦɟɪɧɨɫɬɢ ɪɚɡɜɢɬɢɹ ɩɪɨɦɵɲɥɟɧɧɨɣ ɷɧɟɪɝɟɬɢɤɢ,

ɨɩɪɟɞɟɥɢɬɶ ɬɢɩ ɬɟɯɧɢɱɟɫɤɨɝɨ ɩɪɨɝɪɟɫɫɚ, ɩɨ ɤɨɬɨɪɨɦɭ ɪɚɡɜɢɜɚɟɬɫɹ ɩɪɟɞ-

ɩɪɢɹɬɢɟ, ɧɚɦɟɬɢɬɶ ɩɭɬɢ ɞɚɥɶɧɟɣɲɟɣ ɢɧɬɟɧɫɢɮɢɤɚɰɢɢ ɩɪɨɦɵɲɥɟɧɧɨɝɨ

ɩɪɨɢɡɜɨɞɫɬɜɚ.

Ɋɚɫɫɦɨɬɪɟɧɧɵɟ ɧɚɩɪɚɜɥɟɧɢɹ ɚɧɚɥɢɡɚ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɛɚɥɚɧɫɨɜ

ɩɪɨɦɵɲɥɟɧɧɵɯ ɩɪɟɞɩɪɢɹɬɢɣ ɞɨɥɠɧɵ ɧɚɣɬɢ ɨɬɪɚɠɟɧɢɟ ɜ ɫɨɫɬɚɜɟ ɩɨɤɚ-

ɡɚɬɟɥɟɣ ɢ ɪɚɡɞɟɥɨɜ, ɜɤɥɸɱɚɟɦɵɯ ɜ ɮɨɪɦɭ

ɨɬɱɟɬɧɨɝɨ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɛɚ-

ɥɚɧɫɚ.

2. ɋɢɫɬɟɦɵ ɢ ɢɫɬɨɱɧɢɤɢ ɬɟɩɥɨɫɧɚɛɠɟɧɢɹ

ɗɬɨɬ ɪɚɡɞɟɥ ɤɭɪɫɚ ɧɚɩɢɫɚɧ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɲɢɪɨɤɨ ɢɡɜɟɫɬɧɨɝɨ

ɬɟɩɥɨɷɧɟɪɝɟɬɢɤɚɦ ɭɱɟɛɧɢɤɚ ȿ.ə. ɋɨɤɨɥɨɜɚ «Ɍɟɩɥɨɮɢɤɚɰɢɹ ɢ ɬɟɩɥɨɜɵɟ

ɫɟɬɢ» [1], ɜɵɞɟɪɠɚɜɲɟɝɨ ɜɨɫɟɦɶ ɢɡɞɚɧɢɣ ɡɚ ɬɪɢ ɞɟɫɹɬɤɚ ɥɟɬ.

2.1. Ɍɟɩɥɨɜɨɟ ɩɨɬɪɟɛɥɟɧɢɟ

Ɉɞɧɚ ɢɡ ɩɟɪɜɨɨɱɟɪɟɞɧɵɯ ɡɚɞɚɱ ɩɪɢ ɩɪɨɟɤɬɢɪɨɜɚɧɢɢ ɢ ɪɚɡɪɚɛɨɬɤɟ

ɪɟɠɢɦɚ ɷɤɫɩɥɭɚɬɚɰɢɢ ɫɢɫɬɟɦ ɰɟɧɬɪɚɥɢɡɨɜɚɧɧɨɝɨ ɬɟɩɥɨɫɧɚɛɠɟɧɢɹ ɡɚ-

ɤɥɸɱɚɟɬɫɹ ɜ ɨɩɪɟɞɟɥɟɧɢɢ ɡɧɚɱɟɧɢɣ ɢ ɯɚɪɚɤɬɟɪɚ ɬɟɩɥɨɜɵɯ ɧɚɝɪɭɡɨɤ.

ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɩɪɢ ɩɪɨɟɤɬɢɪɨɜɚɧɢɢ ɭɫɬɚɧɨɜɨɤ ɰɟɧɬɪɚɥɢɡɨ-

ɜɚɧɧɨɝɨ ɬɟɩɥɨɫɧɚɛɠɟɧɢɹ ɨɬɫɭɬɫɬɜɭɸɬ ɞɚɧɧɵɟ ɨ ɪɚɫɱɟɬɧɵɯ ɪɚɫɯɨɞɚɯ ɬɟ-

ɩɥɨɬɵ, ɨɫɧɨɜɚɧɧɵɯ ɧɚ ɩɪɨɟɤɬɚɯ ɬɟɩɥɨɩɨɬɪɟɛɥɹɸɲɢɯ ɭɫɬɚɧɨɜɨɤ ɚɛɨɧɟɧ-

ɬɨɜ, ɪɚɫɱɟɬ ɬɟɩɥɨɜɨɣ ɧɚɝɪɭɡɤɢ ɩɪɨɜɨɞɢɬɫɹ ɧɚ ɨɫɧɨɜɟ ɭɤɪɭɩɧɟɧɧɵɯ ɩɨɤɚ-

ɡɚɬɟɥɟɣ.

2.1.1 ɋɟɡɨɧɧɚɹ ɧɚɝɪɭɡɤɚ

Ɉɫɧɨɜɧɚɹ ɡɚɞɚɱɚ ɨɬɨɩɥɟɧɢɹ ɡɚɤɥɸɱɚɟɬɫɹ ɜ ɩɨɞɞɟɪɠɚɧɢɢ ɜɧɭɬɪɟɧ-

ɧɟɣ ɬɟɦɩɟɪɚɬɭɪɵ ɩɨɦɟɳɟɧɢɣ ɧɚ ɡɚɞɚɧɧɨɦ ɭɪɨɜɧɟ. Ⱦɥɹ ɷɬɨɝɨ ɧɟɨɛɯɨɞɢ-

ɦɨ ɫɨɯɪɚɧɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ ɦɟɠɞɭ ɬɟɩɥɨɜɵɦɢ ɩɨɬɟɪɹɦɢ ɡɞɚɧɢɹ ɢ ɬɟɩɥɨ-

ɩɪɢɬɨɤɨɦ. ɍɫɥɨɜɢɟ ɬɟɩɥɨɜɨɝɨ ɪɚɜɧɨɜɟɫɢɹ ɡɞɚɧɢɹ ɦɨɠɟɬ ɛɵɬɶ ɜɵɪɚɠɟɧɨ

ɜ ɜɢɞɟ ɪɚɜɟɧɫɬɜɚ

Q = Q

= Q

+ Q

ɬɜ

, (2.1)

ɝɞɟ Q

–

ɫɭɦɦɚɪɧɵɟ ɬɟɩɥɨɜɵɟ ɩɨɬɟɪɢ ɡɞɚɧɢɹ;

–

ɬɟɩɥɨɩɨɬɟɪɢ ɬɟɩɥɨ-

ɩɟɪɟɞɚɱɟɣ ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ; Q

–

ɬɟɩɥɨɩɨɬɟɪɢ ɢɧɮɢɥɶɬɪɚɰɢ-

ɟɣ ɢɡ-ɡɚ ɩɨɫɬɭɩɥɟɧɢɹ ɜ ɩɨɦɟɳɟɧɢɟ ɱɟɪɟɡ ɧɟɩɥɨɬɧɨɫɬɢ ɧɚɪɭɠɧɵɯ ɨɝɪɚɠ-

ɞɟɧɢɣ ɯɨɥɨɞɧɨɝɨ ɜɨɡɞɭɯɚ; Q

–

ɩɨɞɜɨɞ ɬɟɩɥɨɬɵ ɜ ɡɞɚɧɢɟ ɱɟɪɟɡ ɨɬɨɩɢ-

ɬɟɥɶɧɭɸ ɫɢɫɬɟɦɭ; Q

ɬɜ

–

ɜɧɭɬɪɟɧɧɢɟ ɬɟɩɥɨɜɵɞɟɥɟɧɢɹ.

Ɍɟɩɥɨɜɵɟ ɩɨɬɟɪɢ ɡɞɚɧɢɹ ɜ ɨɫɧɨɜɧɨɦ ɡɚɜɢɫɹɬ ɨɬ ɩɟɪɜɨɝɨ ɫɥɚɝɚɟɦɨ-

ɝɨ Q

. ɉɨɷɬɨɦɭ ɞɥɹ ɭɞɨɛɫɬɜɚ ɪɚɫɱɟɬɚ ɦɨɠɧɨ ɬɟɩɥɨɜɵɟ ɩɨɬɟɪɢ ɡɞɚɧɢɹ

ɩɪɟɞɫɬɚɜɢɬɶ ɬɚɤ:

Q = Q

(1+μ), (2.2)

ɝɞɟ μ

/ Q

– ɤɨɷɮɮɢɰɢɟɧɬ ɢɧɮɢɥɶɬɪɚɰɢɢ, ɩɪɟɞɫɬɚɜɥɹɸɳɢɣ ɫɨɛɨɣ

ɨɬɧɨɲɟɧɢɟ ɬɟɩɥɨɩɨɬɟɪɶ ɢɧɮɢɥɶɬɪɚɰɢɟɣ ɤ ɬɟɩɥɨɩɨɬɟɪɹɦ ɬɟɩɥɨɩɟɪɟɞɚɱɟɣ

ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ. ɋɥɟɞɭɟɬ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɤɨɷɮɮɢɰɢɟɧɬ ɢɧ-

ɮɢɥɶɬɪɚɰɢɢ ɦɨɠɟɬ ɩɪɢɧɢɦɚɬɶ ɡɧɚɱɟɧɢɹ ɜ ɲɢɪɨɤɨɦ ɞɢɚɩɚɡɨɧɟ.

ɂɫɬɨɱɧɢɤɨɦ ɜɧɭɬɪɟɧɧɢɯ ɬɟɩɥɨɜɵɞɟɥɟɧɢɣ Q

ɬɜ

ɜ ɠɢɥɵɯ ɡɞɚɧɢɹɯ ɹɜ-

ɥɹɸɬɫɹ ɨɛɵɱɧɨ ɥɸɞɢ, ɩɪɢɛɨɪɵ ɞɥɹ ɩɪɢɝɨɬɨɜɥɟɧɢɹ ɩɢɳɢ (ɝɚɡɨɜɵɟ, ɷɥɟɤ-

ɬɪɢɱɟɫɤɢɟ ɢ ɞɪɭɝɢɟ ɩɥɢɬɵ), ɨɫɜɟɬɢɬɟɥɶɧɵɟ ɩɪɢɛɨɪɵ. ɗɬɢ ɬɟɩɥɨɜɵɞɟɥɟ-

ɧɢɹ ɧɨɫɹɬ ɜ ɡɧɚɱɢɬɟɥɶɧɨɣ ɦɟɪɟ ɫɥɭɱɚɣɧɵɣ ɯɚɪɚɤɬɟɪ ɢ ɧɟ ɩɨɞɞɚɸɬɫɹ ɧɢ-

ɤɚɤɨɦɭ ɪɟɝɭɥɢɪɨɜɚɧɢɸ ɜɨ ɜɪɟɦɟɧɢ.

Ⱦɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɜ ɠɢɥɵɯ ɪɚɣɨɧɚɯ ɧɨɪɦɚɥɶɧɨɝɨ ɬɟɦɩɟɪɚɬɭɪɧɨɝɨ

ɪɟɠɢɦɚ ɜɨ ɜɫɟɯ ɨɬɚɩɥɢɜɚɟɦɵɯ ɩɨɦɟɳɟɧɢɹɯ ɨɛɵɱɧɨ ɭɫɬɚɧɚɜɥɢɜɚɸɬ ɝɢɞ-

ɪɚɜɥɢɱɟɫɤɢɣ ɢ ɬɟɦɩɟɪɚɬɭɪɧɵɣ ɪɟɠɢɦ ɬɟɩɥɨɜɨɣ ɫɟɬɢ ɩɨ ɧɚɢɛɨɥɟɟ ɧɟ-

ɜɵɝɨɞɧɵɦ ɭɫɥɨɜɢɹɦ, ɬ. ɟ

. ɩɨ ɪɟɠɢɦɭ ɨɬɨɩɥɟɧɢɹ ɩɨɦɟɳɟɧɢɣ ɫ ɧɭɥɟɜɵɦɢ

ɬɟɩɥɨɜɵɞɟɥɟɧɢɹɦɢ

(

ɬɜ

Ɉ).

ȼɧɭɬɪɟɧɧɢɟ ɬɟɩɥɨɜɵɞɟɥɟɧɢɹ ɩɪɨɦɵɲɥɟɧ-

ɧɵɯ ɩɪɟɞɩɪɢɹɬɢɣ ɞɨɜɨɥɶɧɨ ɭɫɬɨɣɱɢɜɵ ɢ ɧɟɪɟɞɤɨ ɩɪɟɞɫɬɚɜɥɹɸɬ ɫɭɳɟɫɬ-

ɜɟɧɧɭɸ ɞɨɥɸ ɪɚɫɱɟɬɧɨɣ ɨɬɨɩɢɬɟɥɶɧɨɣ ɧɚɝɪɭɡɤɢ, ɩɨɷɬɨɦɭ ɨɧɢ ɞɨɥɠɧɵ

ɭɱɢɬɵɜɚɬɶɫɹ ɩɪɢ ɪɚɡɪɚɛɨɬɤɟ ɪɟɠɢɦɚ ɬɟɩɥɨɫɧɚɛɠɟɧɢɹ ɩɪɨɦɵɲɥɟɧɧɵɯ

ɪɚɣɨɧɨɜ.

Ɍɟɩɥɨɩɨɬɟɪɢ ɩɭɬɟɦ ɬɟɩɥɨɩɟɪɟɞɚɱɢ ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ

ɡɞɚɧɢɹ ɨɩɪɟɞɟɥɢɬɫɹ ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɬɟɦɩɟɪɚɬɭɪɵ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ –

ɢ ɨɬ ɭɫɪɟɞɧɟɧɧɨɣ ɬɟɦɩɟɪɚɬɭɪɵ ɜɧɭɬɪɟɧɧɟɝɨ ɜɨɡɞɭɯɚ ɨɬɚɩɥɢɜɚɟɦɵɯ

ɩɨɦɟɳɟɧɢɣ – t

. Ɉɛɵɱɧɨ ɢɫɩɨɥɶɡɭɸɬ ɪɚɫɱɟɬɧɭɸ ɬɟɦɩɟɪɚɬɭɪɭ ɜɨɡɞɭɯɚ

ɜɧɭɬɪɢ ɩɨɦɟɳɟɧɢɣ

ɜ.ɪ

, ɤɨɬɨɪɚɹ ɩɪɢɧɢɦɚɟɬɫɹ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ ɫɚɧɢɬɚɪ-

ɧɵɦɢ ɧɨɪɦɚɦɢ – ɋɇɢɉ.

= q

V(t

– t

), (2.3)

ɚ ɩɨɥɧɵɟ ɬɟɩɥɨɩɨɬɟɪɢ ɫ ɭɱɟɬɨɦ ɢɧɮɢɥɶɬɪɚɰɢɢ

= q

V(1+μ) (t

– t

). (2.4)

Ɂɞɟɫɶ: V – ɨɛɴɟɦ ɡɞɚɧɢɹ, ɦ

, ɤɨɬɨɪɵɣ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɧɚɪɭɠɧɨɦɭ

ɨɛɦɟɪɭ; q

– ɭɞɟɥɶɧɚɹ ɬɟɩɥɨɩɨɬɟɪɹ ɡɞɚɧɢɹ, ȼɬ/(ɦ

Ʉ).

Ⱦɥɹ ɠɢɥɵɯ ɢ ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɩɪɢ ɩɪɚɜɢɥɶɧɨɣ ɷɤɫɩɥɭɚɬɚ-

ɰɢɢ ɦɚɤɫɢɦɚɥɶɧɵɣ ɤɨɷɮɮɢɰɢɟɧɬ ɢɧɮɢɥɶɬɪɚɰɢɢ ɜ ɛɨɥɶɲɢɧɫɬɜɟ ɫɥɭɱɚɟɜ

ɫɨɫɬɚɜɥɹɟɬ 3–6 %, ɱɬɨ ɥɟɠɢɬ ɜ ɩɪɟɞɟɥɚɯ ɩɨɝɪɟɲɧɨɫɬɢ ɪɚɫɱɟɬɚ ɬɟɩɥɨɩɨ-

ɬɟɪɶ. ɉɨɷɬɨɦɭ ɞɥɹ ɭɩɪɨɳɟɧɢɹ ɢɧɮɢɥɶɬɪɚɰɢɸ ɧɟ ɜɜɨɞɹɬ ɜ ɪɚɫɱɟɬ, ɬ. ɟ.

ɩɪɢɧɢɦɚɸɬ μ = 0. Ⱦɥɹ ɭɱɟɬɚ ɢɧɮɢɥɶɬɪɚɰɢɢ ɡɧɚɱɟɧɢɟ ɭɞɟɥɶɧɵɯ ɬɟɩɥɨɩɨ-

ɬɟɪɶ ɩɪɢɧɢɦɚɸɬ ɫ ɧɟɛɨɥɶɲɢɦ ɡɚɩɚɫɨɦ.

Ɍɟɩɥɨɩɨɬɟɪɢ ɢɧɮɢɥɶɬɪɚɰɢɟɣ ɩɪɨɦɵɲɥɟɧɧɵɯ

ɡɞɚɧɢɣ

ɧɟɪɟɞɤɨ

ɞɨɫɬɢɝɚɸɬ 25–30 % ɬɟɩɥɨɩɨɬɟɪɶ ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ, ɢ ɢɯ ɧɟ-

ɨɛɯɨɞɢɦɨ ɭɱɢɬɵɜɚɬɶ ɩɪɢ ɪɚɫɱɟɬɟ.

Ʉɚɤ ɜɢɞɧɨ ɢɡ (2.3), ɦɚɤɫɢɦɚɥɶɧɵɟ ɬɟɩɥɨɩɨɬɟɪɢ ɬɟɩɥɨɩɟɪɟɞɚɱɟɣ

ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚɠɞɟɧɢɹ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɦɢɧɢɦɚɥɶɧɨɦɭ ɡɧɚɱɟɧɢɸ t

ɬ. ɟ. ɦɢɧɢɦɚɥɶɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ. ȿɫɬɟɫɬɜɟɧɧɨ, ɜɨɡɧɢ-

ɤɚɟɬ ɜɨɩɪɨɫ, ɩɨ ɤɚɤɨɣ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ ɫɥɟɞɭɟɬ ɨɩɪɟɞɟɥɹɬɶ ɪɚɫ-

ɱɟɬɧɵɣ ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ. ȿɫɥɢ ɷɬɨ ɜɵɩɨɥɧɹɬɶ ɩɨ ɦɢɧɢ-

ɦɚɥɶɧɨɣ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ, ɤɨɝɞɚ-ɥɢɛɨ ɧɚɛɥɸɞɚɜɲɟɣɫɹ ɜ ɞɚɧɧɨɣ

ɦɟɫɬɧɨɫɬɢ, ɬɨ ɩɨɥɭɱɚɬɫɹ ɱɪɟɡɦɟɪɧɨ ɡɚɜɵɲɟɧɧɵɟ ɦɨɳɧɨɫɬɢ ɬɟɩɥɨɜɵɯ

ɭɫɬɚɧɨɜɨɤ, ɬɚɤ ɤɚɤ ɦɢɧɢɦɚɥɶɧɚɹ ɧɚɪɭɠɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ ɢɦɟɟɬ, ɤɚɤ ɩɪɚ-

ɜɢɥɨ, ɜɟɫɶɦɚ ɤɪɚɬɤɨɜɪɟɦɟɧɧɵɣ ɯɚɪɚɤɬɟɪ.

ɉɨɷɬɨɦɭ ɩɪɢ ɨɩɪɟɞɟɥɟɧɢɢ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ ɢɫɯɨɞɹɬ

ɧɟ ɢɡ ɦɢɧɢɦɚɥɶɧɨɝɨ ɡɧɚɱɟɧɢɹ ɧɚɪɭɠɧɨɣ

ɬɟɦɩɟɪɚɬɭɪɵ, ɚ ɢɡ ɞɪɭɝɨɝɨ, ɛɨ-

ɥɟɟ ɜɵɫɨɤɨɝɨ, ɬɚɤ ɧɚɡɵɜɚɟɦɨɝɨ ɪɚɫɱɟɬɧɨɝɨ, ɡɧɚɱɟɧɢɹ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟ-

ɪɚɬɭɪɵ ɞɥɹ ɨɬɨɩɥɟɧɢɹ t

ɧɨ

, ɪɚɜɧɨɣ ɫɪɟɞɧɟɣ ɬɟɦɩɟɪɚɬɭɪɟ ɧɚɢɛɨɥɟɟ ɯɨɥɨɞ-

ɧɵɯ ɩɹɬɢɞɧɟɜɨɤ, ɜɡɹɬɵɯ ɢɡ ɜɨɫɶɦɢ ɧɚɢɛɨɥɟɟ ɯɨɥɨɞɧɵɯ ɡɢɦ ɡɚ 50-ɥɟɬɧɢɣ

ɩɟɪɢɨɞ. ȼ ɩɪɢɥɨɠɟɧɢɢ 1 ɜ ɤɨɧɰɟ ɤɧɢɝɢ ɩɪɢɜɟɞɟɧɵ ɪɚɫɱɟɬɧɵɟ ɧɚɪɭɠɧɵɟ

ɬɟɦɩɟɪɚɬɭɪɵ ɞɥɹ ɪɹɞɚ ɝɨɪɨɞɨɜ ɛɵɜɲɟɝɨ ɋɋɋɊ.

ɍɞɟɥɶɧɵɟ ɬɟɩɥɨɩɨɬɟɪɢ ɠɢɥɵɯ ɢ ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɫ ɧɚɪɭɠ-

ɧɵɦ ɨɛɴɟɦɨɦ V > 3000 ɦ

, ɫɨɨɪɭɠɟɧɧɵɯ ɩɨ ɧɨɜɵɦ ɩɪɨɟɤɬɚɦ ɩɨɫɥɟ

1985 ɝ., ɚ ɬɚɤɠɟ ɛɨɥɟɟ ɭɬɟɩɥɟɧɧɵɯ ɡɞɚɧɢɣ, ɫɨɨɪɭɠɟɧɧɵɯ ɪɚɧɟɟ, ɜ ɪɚɣ-

ɨɧɚɯ ɫ ɪɚɫɱɟɬɧɨɣ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ ɞɥɹ ɨɬɨɩɥɟɧɢɹ t

ɧɨ

= –30 °ɋ

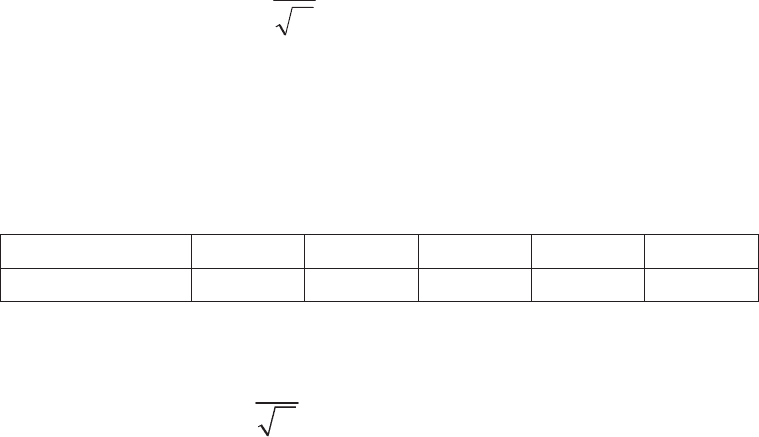
ɦɨɝɭɬ ɛɵɬɶ ɨɪɢɟɧɬɢɪɨɜɨɱɧɨ ɜɵɱɢɫɥɟɧɵ ɤɚɤ

(2.5)

ɝɞɟ a = 1,85 Ⱦɠ / (ɦ

2,5

·ɋ ·Ʉ) = 1,72 ɤɤɚɥ / (ɦ

2,5

· ɱ ·°ɋ).

Ⱦɥɹ ɪɚɣɨɧɨɜ ɫ ɞɪɭɝɨɣ ɪɚɫɱɟɬɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ ɞɥɹ ɨɬɨɩɥɟɧɢɹ ɤ

ɡɧɚɱɟɧɢɹɦ q

, ɜɵɱɢɫɥɟɧɧɵɦ ɩɨ ɮɨɪɦɭɥɟ (2.5), ɜɜɨɞɹɬɫɹ ɫɥɟɞɭɸɳɢɟ ɩɨ-

ɩɪɚɜɨɱɧɵɟ ɤɨɷɮɮɢɰɢɟɧɬɵ:

ɧɨ

°C –10 –20 –30 –40 –50

ȕ 1,3 1,1 1,0 0,9 0,85

ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɮɨɪɦɭɥɚ (2.5) ɩɪɢɦɟɬ ɜɢɞ:



(2.5’)

ɉɪɢ ɨɩɪɟɞɟɥɟɧɢɢ ɬɟɩɥɨɜɨɣ ɧɚɝɪɭɡɤɢ ɜɧɨɜɶ ɡɚɫɬɪɚɢɜɚɟɦɵɯ ɪɚɣ-

ɨɧɨɜ ɢ ɨɬɫɭɬɫɬɜɢɢ ɞɚɧɧɵɯ ɨ ɬɢɩɟ ɢ ɪɚɡɦɟɪɚɯ ɧɚɦɟɱɚɟɦɵɯ ɤ ɫɨɨɪɭɠɟɧɢɸ

ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɦɨɠɧɨ ɨɪɢɟɧɬɢɪɨɜɨɱɧɨ ɩɪɢɧɹɬɶ ɪɚɫɱɟɬɧɵɣ ɪɚɫ-

ɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɪɚɜɧɵɦ 25 % ɪɚɫɱɟɬ-

ɧɨɝɨ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ ɠɢɥɵɯ ɡɞɚɧɢɣ ɪɚɣɨɧɚ.

Ɂɧɚɱɟɧɢɹ ɭɞɟɥɶɧɵɯ ɬɟɩɥɨɩɨɬɟɪɶ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɪɚɡɥɢɱ-

ɧɨɝɨ ɨɛɴɟɦɚ

ɢ ɧɚɡɧɚɱɟɧɢɹ ɩɪɢɜɟɞɟɧɵ ɜ ɩɪɢɥɨɠɟɧɢɢ 4. ɂɦɢ ɦɨɠɧɨ ɩɨɥɶ-

ɡɨɜɚɬɶɫɹ ɩɪɢ ɨɪɢɟɧɬɢɪɨɜɨɱɧɨɦ ɪɚɫɱɟɬɟ ɩɨ ɭɤɪɭɩɧɟɧɧɵɦ ɩɨɤɚɡɚɬɟɥɹɦ

ɨɬɨɩɢɬɟɥɶɧɨɣ ɧɚɝɪɭɡɤɢ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɜɨ ɜɫɟɯ ɤɥɢɦɚɬɢɱɟɫɤɢɯ

ɪɚɣɨɧɚɯ.

ɂɧɮɢɥɶɬɪɚɰɢɹ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ ɜ ɩɨɦɟɳɟɧɢɹɯ ɩɪɨɢɫɯɨɞɢɬ ɩɨɞ

ɞɟɣɫɬɜɢɟɦ ɩɟɪɟɩɚɞɚ (ɪɚɡɧɨɫɬɢ) ɞɚɜɥɟɧɢɣ ɧɚɪɭɠɧɨɝɨ ɢ ɜɧɭɬɪɟɧɧɟɝɨ ɜɨɡ-

ɞɭɯɚ. ɗɬɨɬ ɩɟɪɟɩɚɞ ɞɚɜɥɟɧɢɣ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɫɭɦɦɭ ɞɜɭɯ ɫɥɚɝɚɟ-

ɦɵɯ: ɝɪɚɜɢɬɚɰɢɨɧɧɨɝɨ ɢ ɜɟɬɪɨɜɨɝɨ.

Ɋɚɫɱɟɬɧɵɦɢ ɬɟɩɥɨɩɨɬɟɪɹɦɢ ɧɚɡɵɜɚɸɬɫɹ ɬɟɩɥɨɩɨɬɟɪɢ ɩɪɢ ɪɚɫɱɟɬ-

ɧɨɣ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ t

ɧ.ɨ

. ȼ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (2.4) ɪɚɫɱɟɬɧɵɟ ɬɟɩɥɨ-

ɩɨɬɟɪɢ ɡɞɚɧɢɹ ɫ ɭɱɟɬɨɦ ɢɧɮɢɥɶɬɪɚɰɢɢ

Q' = (1 + ȝ) q

V (t

ɜ.

–

ɧ.ɨ

). (2.6)

ɉɪɢ ɩɨɫɬɨɹɧɧɨɦ ɡɧɚɱɟɧɢɢ ɤɨɷɮɮɢɰɢɟɧɬɚ ɢɧɮɢɥɶɬɪɚɰɢɢ ɡɞɚɧɢɹ

ɨɬɧɨɲɟɧɢɟ ɬɟɩɥɨɩɨɬɟɪɶ Q ɞɚɧɧɨɝɨ ɡɞɚɧɢɹ ɢɥɢ ɝɪɭɩɩɵ ɡɞɚɧɢɣ ɩɪɢ ɥɸ-

ɛɨɣ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ t

> t

ɧ.ɨ

ɤ ɪɚɫɱɟɬɧɵɦ ɬɟɩɥɨɩɨɬɟɪɹɦ ɨɩɪɟɞɟ-

ɥɢɬɫɹ ɤɚɤ ɨɬɧɨɲɟɧɢɟ ɪɚɡɧɨɫɬɟɣ ɬɟɦɩɟɪɚɬɭɪ

ɧ.ɨɜ.ɪ

ɧɜ.ɪ



(2.7)

Ⱦɟɣɫɬɜɭɸɳɢɦɢ ɜ ɧɚɲɟɣ ɫɬɪɚɧɟ ɫɬɪɨɢɬɟɥɶɧɵɦɢ ɧɨɪɦɚɦɢ ɢ ɩɪɚɜɢ-

ɥɚɦ ɢ ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶ ɨɬɨɩɢɬɟɥɶɧɨɝɨ ɩɟɪɢɨɞɚ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɱɢɫ-

ɥɭ ɞɧɟɣ ɫ ɭɫɬɨɣɱɢɜɨɣ ɫɪɟɞɧɟɫɭɬɨɱɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ +8 °ɋ ɢ ɧɢɠɟ.

ɗɬɭ ɧɚɪɭɠɧɭɸ ɬɟɦɩɟɪɚɬɭɪɭ ɨɛɵɱɧɨ ɫɱɢɬɚɸɬ ɧɚɱɚɥɨɦ ɢ ɤɨɧɰɨɦ ɨɬɨɩɢ-

ɬɟɥɶɧɨɝɨ ɩɟɪɢɨɞɚ t

ɧ.ɤ

°ɋ. Ɉɞɧɚɤɨ ɷɤɫɩɥɭɚɬɚɰɢɨɧɧɵɟ ɧɚɛɥɸɞɟɧɢɹ ɩɨɤɚ-

ɡɵɜɚɸɬ, ɱɬɨ ɧɟɥɶɡɹ ɨɫɬɚɜɥɹɬɶ ɠɢɥɵɟ ɢ ɨɛɳɟɫɬɜɟɧɧɵɟ ɡɞɚɧɢɹ ɛɟɡ ɨɬɨ-

ɩɥɟɧɢɹ ɜ ɬɟɱɟɧɢɟ ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɝɨ ɜɪɟɦɟɧɢ ɩɪɢ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭ-

ɪɟ ɧɢɠɟ +10… + 12 °ɋ, ɬɚɤ ɤɚɤ ɷɬɨ ɩɪɢɜɨɞɢɬ ɤ ɡɚɦɟɬɧɨɦɭ ɫɧɢɠɟɧɢɸ

ɜɧɭɬɪɟɧɧɟɣ ɬɟɦɩɟɪɚɬɭɪɵ ɜ ɩɨɦɟɳɟɧɢɢ ɢ ɧɟɛɥɚɝɨɩɪɢɹɬɧɨ ɨɬɪɚɠɚɟɬɫɹ ɧɚ

ɫɚɦɨɱɭɜɫɬɜɢɢ ɧɚɫɟɥɟɧɢɹ.

ɉɟɪɟɯɨɞ ɨɬ ɞɢɪɟɤɬɢɜɧɨɣ ɷɤɨɧɨɦɢɤɢ ɤ ɪɵɧɨɱɧɨɣ ɜ

ɩɪɢɧɰɢɩɟ ɫɧɢ-

ɦɚɟɬ ɤɚɤɢɟ-ɥɢɛɨ ɨɝɪɚɧɢɱɟɧɢɹ ɜ ɧɚɡɧɚɱɟɧɢɢ ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɢ ɨɬɨɩɢ-

ɬɟɥɶɧɨɝɨ ɩɟɪɢɨɞɚ. ɗɬɭ ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶ (ɧɚɱɚɥɨ ɢ ɤɨɧɟɰ) ɨɩɪɟɞɟɥɹɟɬ

ɩɨɬɪɟɛɢɬɟɥɶ ɬɟɩɥɨɜɨɣ ɷɧɟɪɝɢɢ – ɚɛɨɧɟɧɬ ɷɧɟɪɝɨɫɧɚɛɠɚɸɳɟɣ ɨɪɝɚɧɢ-

ɡɚɰɢɢ. ȼ ɬɨ ɠɟ ɜɪɟɦɹ ɞɥɹ ɷɧɟɪɝɨɫɧɚɛɠɚɸɳɟɣ ɨɪɝɚɧɢɡɚɰɢɢ ɜɚɠɧɨ ɡɧɚɬɶ

ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɶ ɩɟɪɢɨɞɚ, ɜ ɬɟɱɟɧɢɟ ɤɨɬɨɪɨɝɨ ɛɭɞɟɬ ɢɦɟɬɶ ɦɟɫɬɨ

ɫɩɪɨɫ ɧɚ ɬɟɩɥɨɬɭ, ɩɨɞɥɟɠɚɳɢɣ ɭɞɨɜɥɟɬɜɨɪɟɧɢɸ ɷɧɟɪɝɨɫɧɚɛɠɚɸɳɟɣ ɨɪ-

ɝɚɧɢɡɚɰɢɟɣ. Ɍɚɤɨɣ

ɫɩɪɨɫ ɧɚ ɬɟɩɥɨɬɭ ɞɨɥɠɟɧ ɨɩɪɟɞɟɥɹɬɶɫɹ, ɤɚɤ ɩɪɚɜɢɥɨ,

ɧɚ ɨɫɧɨɜɚɧɢɢ ɦɧɨɝɨɥɟɬɧɢɯ ɫɬɚɬɢɫɬɢɱɟɫɤɢɯ ɞɚɧɧɵɯ ɫ ɭɱɟɬɨɦ ɩɪɨɝɧɨɡɚ

ɪɨɫɬɚ (ɫɧɢɠɟɧɢɹ) ɩɪɢɫɨɟɞɢɧɟɧɧɵɯ ɤ ɬɟɩɥɨɜɵɦ ɫɟɬɹɦ ɬɟɩɥɨɜɵɯ ɧɚɝɪɭ-

ɡɨɤ. ɇɨɪɦɵ ɋɇɢɉ ɞɨɥɠɧɵ ɩɪɢɦɟɧɹɬɶɫɹ ɜ ɨɫɧɨɜɧɨɦ ɩɪɢ ɪɟɲɟɧɢɢ ɩɪɨ-

ɟɤɬɧɵɯ, ɚ ɧɟ ɷɤɫɩɥɭɚɬɚɰɢɨɧɧɵɯ ɡɚɞɚɱ.

ȼ ɩɪɢɥɨɠɟɧɢɢ 3 ɩɪɢɜɟɞɟɧɵ ɞɚɧɧɵɟ ɨ ɞɥɢɬɟɥɶɧɨɫɬɢ ɫɬɨɹɧɢɹ ɪɚɡ-

ɥɢɱɧɵɯ ɬɟɦɩɟɪɚɬɭɪ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ ɡɚ ɨɬɨɩɢɬɟɥɶɧɵɣ ɩɟɪɢɨɞ ɜ ɧɟɤɨ-

ɬɨɪɵɯ ɝɨɪɨɞɚɯ ɛɵɜɲɟɝɨ ɋɋɋɊ, ɢɦɢ ɦɨɠɧɨ ɩɨɥɶɡɨɜɚɬɶɫɹ ɞɥɹ ɨɪɢɟɧɬɢɪɨ-

ɜɨɱɧɵɯ ɪɚɫɱɟɬɨɜ ɩɪɢ ɨɬɫɭɬɫɬɜɢɢ ɛɨɥɟɟ ɬɨɱɧɵɯ ɫɜɟɞɟɧɢɣ. ɇɚɱɚɥɨ ɢ ɤɨ

ɧɟɰ ɨɬɨɩɢɬɟɥɶɧɨɝɨ ɫɟɡɨɧɚ ɞɥɹ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɨɩɪɟɞɟɥɹɸɬɫɹ ɧɚ-

ɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ, ɩɪɢ ɤɨɬɨɪɨɣ ɬɟɩɥɨɩɨɬɟɪɢ ɱɟɪɟɡ ɧɚɪɭɠɧɵɟ ɨɝɪɚ-

ɠɞɟɧɢɹ ɞɟɥɚɸɬɫɹ ɪɚɜɧɵɦɢ ɜɧɭɬɪɟɧɧɢɦ ɬɟɩɥɨɜɵɞɟɥɟɧɢɹɦ. Ɍɚɤ ɤɚɤ ɬɟɩ-

ɥɨɜɵɞɟɥɟɧɢɹ ɜ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɹɯ ɡɧɚɱɢɬɟɥɶɧɵ, ɬɨ ɜ ɛɨɥɶɲɢɧɫɬɜɟ

ɫɥɭɱɚɟɜ ɞɥɢɬɟɥɶɧɨɫɬɶ ɨɬɨɩɢɬɟɥɶɧɨɝɨ ɫɟɡɨɧɚ ɞɥɹ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ

ɤɨɪɨɱɟ, ɱɟɦ ɞɥɹ ɠɢɥɵɯ ɢ ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ.

2.1.2. ȼɟɧɬɢɥɹɰɢɹ

Ɋɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɩɪɟɞɩɪɢɹɬɢɣ, ɚ ɬɚɤɠɟ ɨɛɳɟɫɬɜɟɧ-

ɧɵɯ ɡɞɚɧɢɣ ɢ ɤɭɥɶɬɭɪɧɵɯ ɭɱɪɟɠɞɟɧɢɣ ɫɨɫɬɚɜɥɹɟɬ ɡɧɚɱɢɬɟɥɶɧɭɸ ɞɨɥɸ

ɫɭɦɦɚɪɧɨɝɨ ɬɟɩɥɨɩɨɬɪɟɛɥɟɧɢɹ ɨɛɴɟɤɬɚ. ȼ ɩɪɨɢɡɜɨɞɫɬɜɟɧɧɵɯ ɩɪɟɞɩɪɢ-

ɹɬɢɹɯ ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɱɚɫɬɨ ɩɪɟɜɵɲɚɟɬ ɪɚɫɯɨɞ ɧɚ ɨɬɨ-

ɩɥɟɧɢɟ.

Ɋɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɩɪɢɧɢɦɚɸɬ ɩɨ ɩɪɨɟɤɬɚɦ ɦɟɫɬɧɵɯ ɫɢɫɬɟɦ

ɜɟɧɬɢɥɹɰɢɢ ɢɥɢ ɩɨ ɬɢɩɨɜɵɦ ɩɪɨɟɤɬɚɦ ɡɞɚɧɢɣ, ɚ ɞɥɹ ɞɟɣɫɬɜɭɸɳɢɯ

ɭɫɬɚ-

ɧɨɜɨɤ – ɩɨ ɷɤɫɩɥɭɚɬɚɰɢɨɧɧɵɦ ɞɚɧɧɵɦ.

Ɉɪɢɟɧɬɢɪɨɜɨɱɧɵɣ ɪɚɫɱɟɬ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ, Ⱦɠ/ɫ

ɢɥɢ ɤɤɚɥ/ɱ, ɦɨɠɧɨ ɩɪɨɜɨɞɢɬɶ ɩɨ ɮɨɪɦɭɥɟ

= mV

ɜ.ɩ

– t

), (2.8)

ɝɞɟ q

– ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ; m – ɤɪɚɬɧɨɫɬɶ ɨɛɦɟɧɚ ɜɨɡɞɭɯɚ,

1/ɫ ɢɥɢ l/ɱ; V

– ɜɟɧɬɢɥɢɪɭɟɦɵɣ ɨɛɴɟɦ ɡɞɚɧɢɹ, ɦ

; c

– ɨɛɴɟɦɧɚɹ ɬɟɩɥɨ-

ɟɦɤɨɫɬɶ ɜɨɡɞɭɯɚ, ɪɚɜɧɚɹ 1,26 ɤȾɠ/(ɦ

/Ʉ) = 0,3 ɤɤɚɥ/(ɦ

/ °ɋ); t

ɜ.ɩ

– ɬɟɦ-

ɩɟɪɚɬɭɪɚ ɧɚɝɪɟɬɨɝɨ ɜɨɡɞɭɯɚ, ɩɨɞɚɜɚɟɦɨɝɨ ɜ ɩɨɦɟɳɟɧɢɟ, °ɋ; t

– ɬɟɦ-

ɩɟɪɚɬɭɪɚ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ, °ɋ.

Ⱦɥɹ ɭɞɨɛɫɬɜɚ ɪɚɫɱɟɬɚ (2.8) ɩɪɢɜɨɞɹɬ ɤ ɜɢɞɭ

= q

V (t

– t

), (2.9)

ɝɞɟ q

– ɭɞɟɥɶɧɵɣ ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ, ɬ. ɟ. ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ

ɧɚ 1 ɦ

ɜɟɧɬɢɥɢɪɭɟɦɨɝɨ ɡɞɚɧɢɹ ɩɨ ɧɚɪɭɠɧɨɦɭ ɨɛɦɟɪɭ ɢ ɧɚ 1 °ɋ ɪɚɡɧɨɫɬɢ

ɦɟɠɞɭ ɭɫɪɟɞɧɟɧɧɨɣ ɪɚɫɱɟɬɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ ɜɨɡɞɭɯɚ ɜɧɭɬɪɢ ɜɟɧ-

ɬɢɥɢɪɭɟɦɨɝɨ ɩɨɦɟɳɟɧɢɹ ɢ ɬɟɦɩɟɪɚɬɭɪɨɣ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ; V – ɧɚ-

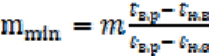
ɪɭɠɧɵɣ ɨɛɴɟɦ ɜɟɧɬɢɥɢɪɭɟɦɨɝɨ ɡɞɚɧɢɹ; t

– ɭɫɪɟɞɧɟɧɧɚɹ ɜɧɭɬɪɟɧɧɹɹ

ɬɟɦɩɟɪɚɬɭɪɚ, °ɋ.

ɂɡ ɫɪɚɜɧɟɧɢɹ (2.8) ɢ (2.9) ɫɥɟɞɭɟɬ, ɱɬɨ ɩɪɢ t

ɜ.ɩ

= t

= mɫ

/ V. (2.10)

ȼ ɩɪɢɥɨɠɟɧɢɢ 4 ɩɪɢɜɟɞɟɧɵ ɡɧɚɱɟɧɢɹ ɭɞɟɥɶɧɵɯ ɪɚɫɯɨɞɨɜ ɬɟɩɥɨɬɵ

ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɩɪɨɦɵɲɥɟɧɧɵɯ, ɚ ɬɚɤɠɟ ɫɥɭɠɟɛɧɵɯ ɢ ɨɛɳɟɫɬɜɟɧɧɵɯ

ɡɞɚɧɢɣ, ɧɚ ɨɫɧɨɜɟ ɤɨɬɨɪɵɯ ɦɨɝɭɬ ɛɵɬɶ ɨɩɪɟɞɟɥɟɧɵ ɪɚɫɱɟɬɧɵɟ ɪɚɫɯɨɞɵ

ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɩɨ ɭɤɪɭɩɧɟɧɧɵɦ ɩɨɤɚɡɚɬɟɥɹɦ ɩɪɢ ɨɪɢɟɧɬɢɪɨ-

ɜɨɱɧɵɯ ɪɚɫɱɟɬɚɯ.

Ⱦɥɹ ɫɧɢɠɟɧɢɹ ɪɚɫɱɟɬɧɨɝɨ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɦɢɧɢ-

ɦɚɥɶɧɚɹ ɧɚɪɭɠɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ, ɩɨ ɤɨɬɨɪɨɣ ɪɚɫɫɱɢɬɵɜɚɸɬɫɹ ɜɟɧɬɢɥɹɰɢ

ɨɧɧɵɟ ɭɫɬɚɧɨɜɤɢ, t

ɧ.ɜ

ɩɪɢɧɢɦɚɟɬɫɹ, ɤɚɤ ɩɪɚɜɢɥɨ, ɜɵɲɟ ɪɚɫɱɟɬɧɨɣ ɬɟɦ-

ɩɟɪɚɬɭɪɵ ɞɥɹ ɨɬɨɩɥɟɧɢɹ t

ɧ.ɨ

. ɉɨ ɞɟɣɫɬɜɭɸɳɢɦ ɧɨɪɦɚɦ ɪɚɫɱɟɬɧɚɹ ɬɟɦɩɟ-

ɪɚɬɭɪɚ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ ɞɥɹ ɩɪɨɟɤɬɢɪɨɜɚɧɢɹ ɜɟɧɬɢɥɹɰɢɢ ɨɩɪɟɞɟɥɹɟɬ-

ɫɹ ɤɚɤ ɫɪɟɞɧɹɹ ɬɟɦɩɟɪɚɬɭɪɚ ɧɚɢɛɨɥɟɟ ɯɨɥɨɞɧɨɝɨ ɩɟɪɢɨɞɚ, ɫɨɫɬɚɜɥɹɸɳɟ-

ɝɨ 15 % ɩɪɨɞɨɥɠɢɬɟɥɶɧɨɫɬɢ ɜɫɟɝɨ ɨɬɨɩɢɬɟɥɶɧɨɝɨ ɩɟɪɢɨɞɚ. ɂɫɤɥɸɱɟɧɢ-

ɟɦ ɹɜɥɹɸɬɫɹ ɬɨɥɶɤɨ ɩɪɨɦɵɲɥɟɧɧɵɟ ɰɟɯɢ ɫ ɛɨɥɶɲɢɦ ɜɵɞɟɥɟɧɢɟɦ ɜɪɟɞ-

ɧɨɫɬɟɣ, ɞɥɹ ɤɨɬɨɪɵɯ t

ɧ.ɜ

ɩɪɢɧɢɦɚɟɬɫɹ ɪɚɜɧɨɣ t

ɧ.ɨ

. Ɂɧɚɱɟɧɢɹ t

ɧ.ɜ

ɞɥɹ ɪɹɞɚ

ɝɨɪɨɞɨɜ ɩɪɢɜɟɞɟɧɵ ɜ ɩɪɢɥɨɠɟɧɢɢ 1.

Ɋɚɫɱɟɬɧɵɣ ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɧɚɯɨɞɢɦ ɩɨ ɮɨɪɦɭɥɟ

= q

V (t

ɜ.

– t

ɧ.ɜ

), (2.9)

ɝɞɟ t

ɜ.ɪ

– ɭɫɪɟɞɧɟɧɧɚɹ ɪɚɫɱɟɬɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ ɜɧɭɬɪɢ ɩɨɦɟɳɟɧɢɹ,

ɋ.

ȿɫɥɢ ɬɟɦɩɟɪɚɬɭɪɚ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ ɫɬɚɧɨɜɢɬɫɹ ɧɢɠɟ t

ɧ.ɜ

, ɬɨ ɪɚɫ-

ɯɨɞ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɞɨɥɟɧ ɨɫɬɚɜɚɬɶɫɹ ɪɚɜɧɵɦ ɪɚɫɱɟɬɧɨɦɭ ɪɚɫ-

ɯɨɞɭ. ɗɬɨ ɞɨɫɬɢɝɚɟɬɫɹ ɫɨɤɪɚɳɟɧɢɟɦ ɤɪɚɬɧɨɫɬɢ ɨɛɦɟɧɚ. ɉɪɢ ɡɚɞɚɧɧɨɣ

ɪɚɫɱɟɬɧɨɣ ɤɪɚɬɧɨɫɬɢ ɨɛɦɟɧɚ m ɦɢɧɢɦɚɥɶɧɚɹ ɤɪɚɬɧɨɫɬɶ ɨɛɦɟɧɚ

min

ɩɪɢ

ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ

ɧ.ɜ

ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɮɨɪɦɭɥɟ

(2.10)

ɝɞɟ m – ɪɚɫɱɟɬɧɚɹ ɤɪɚɬɧɨɫɬɶ ɨɛɦɟɧɚ ɜɨɡɞɭɯɚ.

2.1.3. ɋɭɦɦɚɪɧɚɹ ɫɟɡɨɧɧɚɹ ɬɟɩɥɨɜɚɹ ɧɚɝɪɭɡɤɚ

Ɉɬɨɩɢɬɟɥɶɧɚɹ ɧɚɝɪɭɡɤɚ ɢɦɟɟɬ, ɤɚɤ ɩɪɚɜɢɥɨ, ɤɪɭɝɥɨɫɭɬɨɱɧɵɣ ɯɚ-

ɪɚɤɬɟɪ. ɉɪɢ ɧɟɢɡɦɟɧɧɵɯ ɡɧɚɱɟɧɢɹɯ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɵ, ɫɤɨɪɨɫɬɢ

ɜɟɬɪɚ ɢ ɨɛɥɚɱɧɨɫɬɢ ɨɬɨɩɢɬɟɥɶɧɚɹ ɧɚɝɪɭɡɤɚ ɠɢɥɵɯ ɡɞɚɧɢɣ ɩɪɚɤɬɢɱɟɫɤɢ

ɩɨɫɬɨɹɧɧɚ. Ɉɬɨɩɢɬɟɥɶɧɚɹ ɧɚɝɪɭɡɤɚ ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɢ ɩɪɨɦɵɲ-

ɥɟɧɧɵɯ ɩɪɟɞɩɪɢɹɬɢɣ ɢɦɟɟɬ ɧɟɩɨɫɬɨɹɧɧɵɣ ɫɭɬɨɱɧɵɣ ɝɪɚɮɢɤ, ɤɨɝɞɚ ɜ ɰɟ-

ɥɹɯ ɷɤɨɧɨɦɢɢ ɬɟɩɥɨɬɵ ɢɫɤɭɫɫɬɜɟɧɧɨ ɫɧɢɠɚɸɬ ɩɨɞɚɱɭ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨ-

ɩɥɟɧɢɟ ɜ ɧɟɪɚɛɨɱɢɟ ɱɚɫɵ

(ɧɨɱɧɨɣ ɩɟɪɢɨɞ ɢ ɜɵɯɨɞɧɵɟ ɞɧɢ).

Ɂɧɚɱɢɬɟɥɶɧɨ ɛɨɥɟɟ ɪɟɡɤɨ ɢɡɦɟɧɹɟɬɫɹ ɤɚɤ ɜ ɬɟɱɟɧɢɟ ɫɭɬɨɤ, ɬɚɤ ɢ ɩɨ

ɞɧɹɦ ɧɟɞɟɥɢ ɜɟɧɬɢɥɹɰɢɨɧɧɚɹ ɧɚ-

ɝɪɭɡɤɚ, ɬɚɤ ɤɚɤ ɜ ɧɟɪɚɛɨɱɢɟ ɱɚɫɵ

ɩɪɨɦɵɲɥɟɧɧɵɯ ɩɪɟɞɩɪɢɹɬɢɣ ɢ

ɭɱɪɟɠɞɟɧɢɣ ɜɟɧɬɢɥɹɰɢɹ, ɤɚɤ

ɩɪɚɜɢɥɨ, ɧɟ ɪɚɛɨɬɚɟɬ.

ɋɭɦɦɚɪɧɵɣ ɪɚɫɯɨɞ ɬɟɩɥɨ-

ɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ ɢ ɜɟɧɬɢɥɹɰɢɸ

ɩɨ ɪɚɣɨɧɭ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ

ɫɭɦɦɭ ɪɚɫɯɨɞɨɜ ɨɬɞɟɥɶɧɵɯ

ɚɛɨ-

ɧɟɧɬɨɜ.

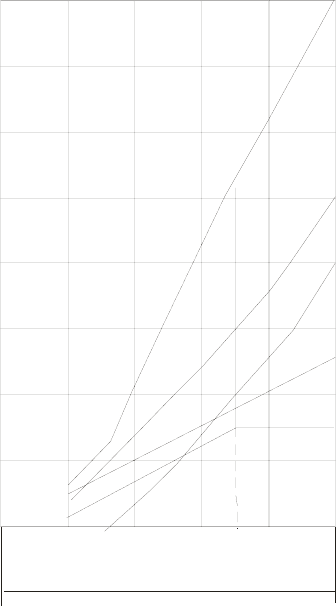
Ⱦɥɹ ɢɥɥɸɫɬɪɚɰɢɢ ɧɚ ɪɢɫ.

2.1 ɩɨɤɚɡɚɧɚ ɡɚɜɢɫɢɦɨɫɬɶ ɪɚɫɯɨɞɚ

ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ ɢ ɜɟɧɬɢɥɹ-

ɰɢɸ ɪɚɣɨɧɚ ɨɬ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟ-

ɪɚɬɭɪɵ. Ɋɚɫɱɟɬɧɵɟ ɬɟɩɥɨɩɨɬɟɪɢ

ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ (ɤɪɢɜɚɹ

1) ɪɚɜɧɵ 500 ɆȾɠ/ɫ. ȼɨɝɧɭɬɵɣ

ɯɚɪɚɤɬɟɪ ɤɪɢɜɨɣ 1 ɨɛɴɹɫɧɹɟɬɫɹ

ɭɱɟɬɨɦ ɢɧɮɢɥɶɬɪɚɰɢɢ.

ɑɚɫɬɶ ɬɟɩɥɨɩɨɬɟɪɶ ɩɪɨ-

ɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɜ ɪɚɡɦɟɪɟ 100 ɆȾɠ/ɫ ɤɨɦɩɟɧɫɢɪɭɟɬɫɹ ɜɧɭɬɪɟɧɧɢɦɢ

ɬɟɩɥɨɜɵɞɟɥɟɧɢɹɦɢ (ɥɢɧɢɹ 2), ɩɨɷɬɨɦɭ ɪɚɫɱɟɬɧɵɣ

ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɧɚ

ɨɬɨɩɥɟɧɢɟ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɦɟɧɶɲɟ ɪɚɫɱɟɬɧɵɯ ɬɟɩɥɨɩɨɬɟɪɶ ɷɬɢɯ

ɡɞɚɧɢɣ ɢ ɫɨɫɬɚɜɥɹɟɬ 400 ɆȾɠ/ɫ (ɤɪɢɜɚɹ 3). ɉɨ ɷɬɨɣ ɠɟ ɩɪɢɱɢɧɟ ɨɬɨɩɥɟ-

ɧɢɟ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɞɨɥɠɧɨ ɜɤɥɸɱɚɬɶɫɹ ɜ ɪɚɛɨɬɭ ɩɪɢ ɧɚɪɭɠɧɨɣ

ɬɟɦɩɟɪɚɬɭɪɟ t

ɧ.ɤ

= +4 °ɋ. ɉɪɢ ɧɚɪɭɠɧɵɯ ɬɟɦɩɟɪɚɬɭɪɚɯ ɜɵɲɟ +4 °ɋ ɬɟɩ-

ɥɨɩɨɬɟɪɢ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɤɨɦɩɟɧɫɢɪɭɸɬɫɹ ɜɧɭɬɪɟɧɧɢɦɢ ɬɟɩɥɨ-

ɜɵɞɟɥɟɧɢɹɦɢ.

ɬɜ

ɆȾɠ/ɫ

700

600

400

500

300

200

100

-100

+18

+10

-10

ɧ.ɜ

-20

ɧ.ɤ

Ɋɢɫ. 2.1. Ɂɚɜɢɫɢɦɨɫɬɶ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ

ɧɚ ɨɬɨɩɥɟɧɢɟ ɢ ɜɟɧɬɢɥɹɰɢɸ ɬɟɦɩɟɪɚ-

ɬɭɪɵ ɧɚɪɭɠɧɨɝɨ ɜɨɡɞɭɯɚ

Q = q

V (t

ɜ.ɪ

– t

ɧ.ɜ

(2.11)

Ƚɪɚɮɢɤ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɜɟɧɬɢɥɹɰɢɸ ɩɪɨɦɵɲɥɟɧɧɵɯ ɢ ɨɛɳɟ-

ɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɢɦɟɟɬ ɢɡɥɨɦ ɩɪɢ ɪɚɫɱɟɬɧɨɣ ɧɚɪɭɠɧɨɣ ɬɟɦɩɟɪɚɬɭɪɟ

ɜɟɧɬɢɥɹɰɢɢ t

ɧ.ɜ

= –15 °ɋ (ɤɪɢɜɚɹ 4). Ƚɪɚɮɢɤ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟ-

ɧɢɟ ɠɢɥɵɯ ɢ ɨɛɳɟɫɬɜɟɧɧɵɯ ɡɞɚɧɢɣ ɩɨɤɚɡɚɧ ɥɢɧɢɟɣ 5. ɋɭɦɦɚɪɧɵɣ ɝɪɚ-

ɮɢɤ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɧɚ ɨɬɨɩɥɟɧɢɟ ɢ ɜɟɧɬɢɥɹɰɢɸ ɩɨ ɪɚɣɨɧɭ ɜ ɰɟɥɨɦ

(ɤɪɢɜɚɹ 6) ɢɦɟɟɬ ɞɜɟ ɬɨɱɤɢ ɢɡɥɨɦɚ: ɨɞɧɭ ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ t

ɧ.ɜ

(ɪɚɫɱɟɬɧɚɹ

ɧɚɪɭɠɧɚɹ ɬɟɦɩɟɪɚɬɭɪɚ ɞɥɹ ɜɟɧɬɢɥɹɰɢɢ), ɞɪɭɝɭɸ – ɩɪɢ ɬɟɦɩɟɪɚɬɭɪɟ

ɧ.ɤ

= +4 °ɋ (ɜɤɥɸɱɟɧɢɟ ɜ ɪɚɛɨɬɭ ɨɬɨɩɥɟɧɢɹ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ).

2.1.4. Ʉɪɭɝɥɨɝɨɞɢɱɧɚɹ ɧɚɝɪɭɡɤɚ

ɉɚɪɚɦɟɬɪɵ ɢ ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ ɞɥɹ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɯ ɧɭɠɞ ɡɚɜɢɫɹɬ

ɨɬ ɯɚɪɚɤɬɟɪɚ ɬɟɯɧɨɥɨɝɢɱɟɫɤɨɝɨ ɩɪɨɰɟɫɫɚ, ɬɢɩɚ ɩɪɨɢɡɜɨɞɫɬɜɟɧɧɨɝɨ ɨɛɨ-

ɪɭɞɨɜɚɧɢɹ, ɨɛɳɟɣ ɨɪɝɚɧɢɡɚɰɢɢ ɪɚɛɨɬ ɢ ɬ. ɞ. ɍɫɨɜɟɪɲɟɧɫɬɜɨɜɚɧɢɟ ɢ ɪɚ-

ɰɢɨɧɚɥɢɡɚɰɢɹ ɬɟɯɧɨɥɨɝɢɱɟɫɤɨɝɨ ɩɪɨɰɟɫɫɚ ɦɨɝɭɬ ɜɵɡɜɚɬɶ ɤɨɪɟɧɧɵɟ ɢɡ-

ɦɟɧɟɧɢɹ ɜ ɪɚɡɦɟɪɟ ɢ ɯɚɪɚɤɬɟɪɟ ɬɟɩɥɨɜɨɣ ɧɚɝɪɭɡɤɢ.

Ⱦɥɹ ɷɤɨɧɨɦɢɢ ɬɨɩɥɢɜɧɨ-ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɪɟɫɭɪɫɨɜ ɫɥɟɞɭɟɬ ɫɨɜɟɪ-

ɲɟɧɫɬɜɨɜɚɬɶ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɟ ɩɪɨɰɟɫɫɵ, ɦɚɤɫɢɦɚɥɶɧɨ ɢɫɩɨɥɶɡɨɜɚɬɶ

ɨɬ-

ɪɚɛɨɬɚɜɲɭɸ ɬɟɩɥɨɬɭ ɞɥɹ ɬɟɯɧɨɥɨɝɢɱɟɫɤɢɯ ɰɟɥɟɣ, ɚ ɩɪɢ ɬɟɩɥɨɫɧɚɛɠɟɧɢɢ

ɨɬ Ɍɗɐ ɦɚɤɫɢɦɚɥɶɧɨ ɢɫɩɨɥɶɡɨɜɚɬɶ ɬɟɩɥɨɧɨɫɢɬɟɥɶ ɛɨɥɟɟ ɧɢɡɤɨɝɨ ɩɨɬɟɧ-

ɰɢɚɥɚ.

ȼ ɫɜɹɡɢ ɫ ɢɧɬɟɧɫɢɜɧɵɦ ɠɢɥɢɳɧɵɦ ɫɬɪɨɢɬɟɥɶɫɬɜɨɦ ɡɧɚɱɢɬɟɥɶɧɨ

ɜɵɪɨɫɥɚ ɧɚɝɪɭɡɤɚ ɝɨɪɹɱɟɝɨ ɜɨɞɨɫɧɚɛɠɟɧɢɹ ɝɨɪɨɞɨɜ. ɗɬɚ ɧɚɝɪɭɡɤɚ ɜɨ

ɦɧɨɝɢɯ ɪɚɣɨɧɚɯ ɫɬɚɧɨɜɢɬɫɹ ɫɨɪɚɡɦɟɪɧɨɣ ɨɬɨɩɢɬɟɥɶɧɨɣ ɧɚɝɪɭɡɤɟ. Ƚɨɞɨ-

ɜɨɣ ɨɬɩɭɫɤ ɬɟɩɥɨɬɵ ɧɚ ɝɨɪɹɱɟɟ ɜɨɞɨɫɧɚɛɠɟɧɢɟ ɠɢɥɵɯ ɪɚɣɨɧɨɜ ɱɚɫɬɨ

ɞɨɫɬɢɝɚɟɬ 35–40 %

ɫɭɦɦɚɪɧɨɝɨ ɝɨɞɨɜɨɝɨ ɪɚɫɯɨɞɚ ɬɟɩɥɨɬɵ ɪɚɣɨɧɚ.

Ƚɨɪɹɱɟɟ ɜɨɞɨɫɧɚɛɠɟɧɢɟ ɢɦɟɟɬ ɜɟɫɶɦɚ ɧɟɪɚɜɧɨɦɟɪɧɵɣ ɯɚɪɚɤɬɟɪ,

ɤɚɤ ɜ ɬɟɱɟɧɢɟ ɫɭɬɨɤ, ɬɚɤ ɢ ɜ ɬɟɱɟɧɢɟ ɧɟɞɟɥɢ. ɇɚɢɛɨɥɶɲɚɹ ɧɚɝɪɭɡɤɚ ɝɨɪɹ-

ɱɟɝɨ ɜɨɞɨɫɧɚɛɠɟɧɢɹ ɜ ɠɢɥɵɯ ɪɚɣɨɧɚɯ ɢɦɟɟɬ ɦɟɫɬɨ, ɤɚɤ ɩɪɚɜɢɥɨ, ɜ ɩɪɟɞ-

ɜɵɯɨɞɧɵɟ ɞɧɢ (ɩɪɢ 5-ɞɧɟɜɧɨɣ ɪɚɛɨɱɟɣ ɧɟɞɟɥɢ ɜ ɩɟɪɜɵɣ ɜɵɯɨɞɧɨɣ ɞɟɧɶ

– ɫɭɛɛɨɬɭ).

ɋɪɟɞɧɟɧɟɞɟɥɶɧɵɣ ɪɚɫɯɨɞ ɬɟɩɥɨɬɵ (ɫɪɟɞɧɟɧɟɞɟɥɶɧɚɹ ɬɟɩɥɨɜɚɹ

ɧɚ-

ɝɪɭɡɤɚ), Ⱦɠ/ɫ, ɛɵɬɨɜɨɝɨ ɝɨɪɹɱɟɝɨ ɜɨɞɨɫɧɚɛɠɟɧɢɹ ɨɬɞɟɥɶɧɵɯ ɠɢɥɵɯ,

ɨɛɳɟɫɬɜɟɧɧɵɯ ɢ ɩɪɨɦɵɲɥɟɧɧɵɯ ɡɞɚɧɢɣ ɢɥɢ ɝɪɭɩɩɵ ɨɞɧɨɬɢɩɧɵɯ ɡɞɚ-

ɧɢɣ ɨɩɪɟɞɟɥɹɟɬɫɹ ɩɨ ɋɇɢɉ 2.04.07.86 «Ɍɟɩɥɨɜɵɟ ɫɟɬɢ» ɩɨ ɫɥɟɞɭɸɳɟɣ

ɮɨɪɦɭɥɟ:

)55)((2,1

ɫɪ

ɫɪ.ɧ

ɫtbam



(2.12)