Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

878 C. C. Tsuei and J.R. Kirtley

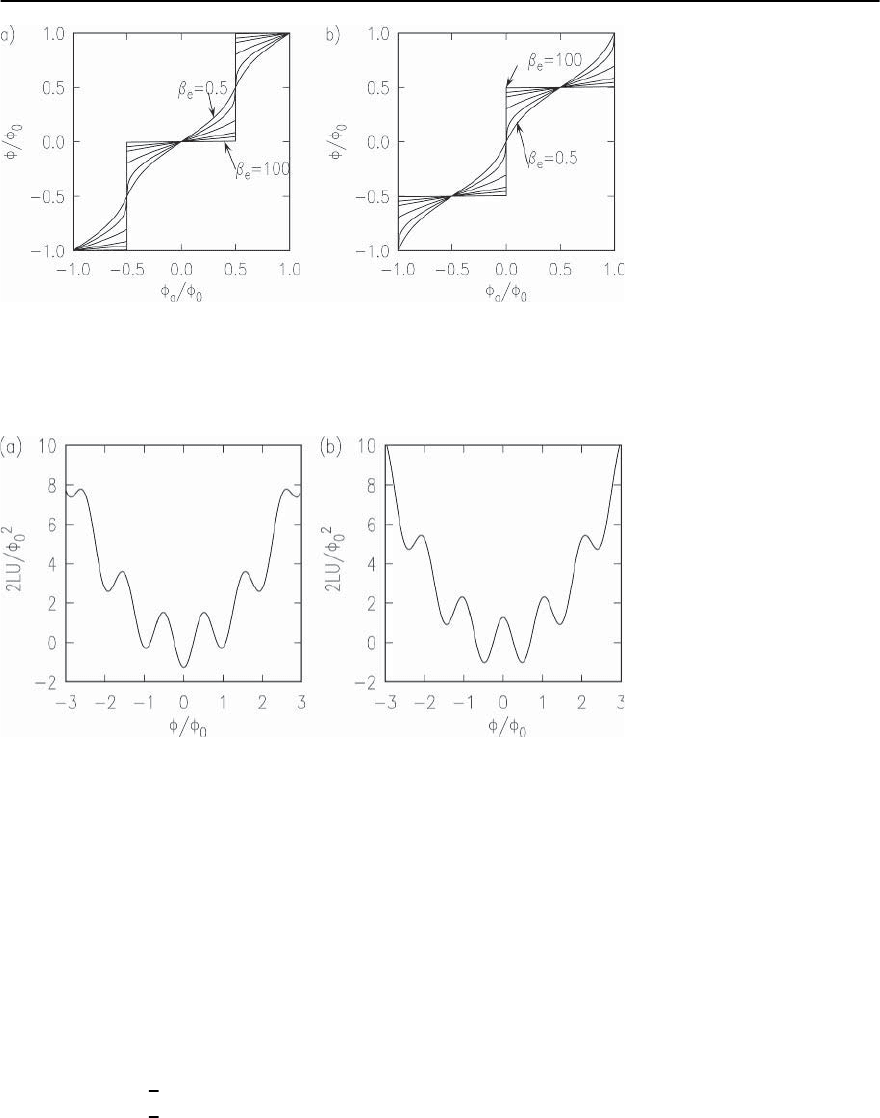
Fig. 16.3. Minimum energy solution of (16.17) for the total ﬂux ¥ /¥

as a function of the externally applied ﬂux ¥

/¥

for

a0-ring(a)and -ring (b), for ˇ

=2 LI

/¥

= 0.5,1,2,5,10,and 100. For small applied fields and ˇ

< 1 the shielding

currents oppose the applied ﬂux for the 0-ring (diamagnetic shielding) and are aligned with the applied ﬂux for the

-ring (paramagnetic shielding). For ˇ

> 1the-ring has spontaneous magnetization with the same sign as small

externally applied fields, approaching total ﬂux ¥ = ¥

/2for¥

=0asˇ

becomes large

Fig. 16.4. Free energy U of a su-

perconducting ring with a sin-

glejunctionin(a)a0-ring,

or (b)a -ring configuration,

with zero external applied field

(16.17), as a function of the

total ﬂux ¥ in the ring. Here

=2LI

/¥

whered is the spacing between superconductors,and

is the supercurrent density in the junction, and Ÿ

is 0 for the 0-section, and  for the -section. As

discussed above, the assignment of 0 or  for the in-

trinsic phase shift of a particular section of the junc-

tion is arbitrary: identical results are obtained if the

assignments are reversed. (r

) is related to the cur-

rent ﬂowing through the junction by the Josephson

relation j

= j

sin((r

)+Ÿ(r

)).

The lowest energy solution of (16.19) for a 0–0-

junction is (r

) = 0: there is no spontaneous mag-

netization.For a 0 − -junction with width W much

wider than the 

s, the solution of (16.19) is [102]

(x)=4tan

−1

[(

√

2−1)e

/

] r

< 0 ,

4tan

−1

[(

√

2+1)e

/

]− r

> 0 .

(16.20)

This is the equation fora Josephson vortex with ¥

total ﬂux. If the width of the junction is compara-

ble to the Josephson penetration depth, the solu-

tion of (16.19) is more difficult [100]. Numerical re-

sults [103] for the total spontaneous ﬂux for a sym-

metric 0− junction(equal widths of intrinsic0 and

 phase shifts) as a function of the reduced width

W/2

are shown as the open symbols in Fig.16.5.As

discussed below, the spontaneous magnetization in

frustrated rings and junctions has been directly ob-

served by magnetic imaging using scanning SQUID

microscopes.

One can also test for frustration in a supercon-

ducting loop by connecting leads to it, and measur-

ing the superconducting critical current through the

16 Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors 879

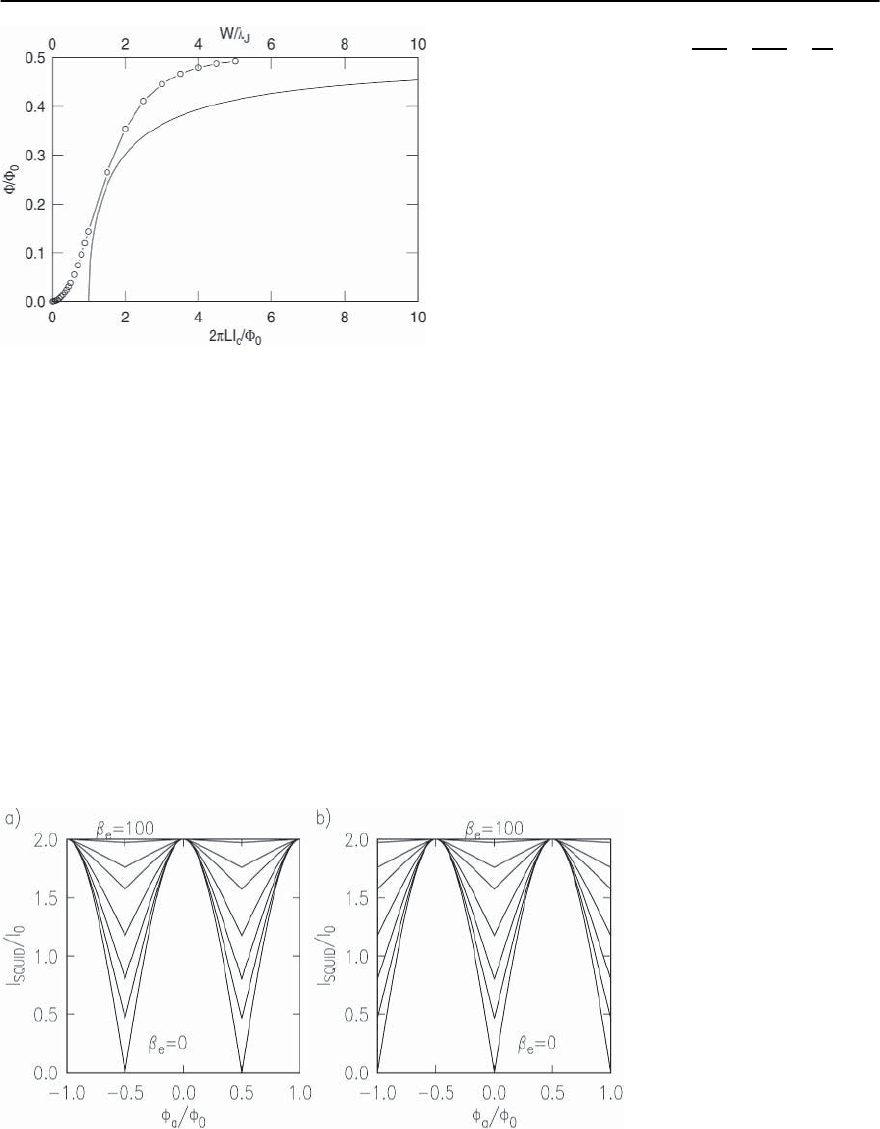
Fig. 16.5. Total spontaneous ﬂux ¥ /¥

,forafrustratedsu-

perconducting ring in zero applied ﬂux ¥

,asafunctionof

=2LI

/¥

(solid line, lower scale),andforasymmetric

0− junction as a function of W/2

(open circles, upper

scale), where W is the total width of the junction,and 

the Josephson penetration depth

loop as a function of the applied ﬂux ¥

.Consider

a closed ring of superconductor interrupted by two

Josephson weak links labeled a and b.Themeasured

critical current of the SQUID is the maximum of

sin 

, (16.21)

where I

)and

(

) are the critical currents and

phases of the a (b)-junctions,respectively. This max-

imum must be calculated subject to the constraint

that the phase be single valued:

2n=

− 

+ Ÿ +2



−



(16.22)

where L

and L

are the effective self-inductances

of the two arms of the ring, and Ÿ =0or for

a0-ringora-ring, respectively. The dependence

of the SQUID critical current I

SQUID

vs. applied ﬂux

is plotted in Fig. 16.6 for a number of different

=2LI

/¥

values. For these plots we have as-

sumed I

= I

,andL

= L

. Asymmetries in

the junctioncriticalcurrent or arm inductances pro-

duce phase shifts in the interference patterns, and

reductions in the modulation depths. The modula-

tion depth decreases as the ˇ

increases.

For junctions with uniform Josephson current

density, and in the “short” junction limit where

the junction size is much smaller than the Joseph-

son penetration depth, the critical current should

follow the standard Fraunhofer pattern I

(¥ )=

|sin(¥/¥

)/(¥/¥

)| as a function of the ﬂux

¥ threading the junction, for an unfrustrated (0–

0) junction. This pattern has a maximum in the

critical current at zero applied field (see Fig. 16.7).

In contrast, a “short” frustrated (0 − )junc-

tion should show the interference pattern I

(¥ )=

|sin

(¥/2¥

)/(¥/2¥

)|,withaminimumat

zero applied ﬂux. As can be seen from Fig. 16.7, as

the ratio of the junction width to the Josephson pen-

etration depth gets larger, the modulation depth of

these interference patterns decrease. Further, inho-

mogeneities in the junction current densities will

Fig. 16.6. Dependence of the

total critical current I

SQUID

through a symmetric conven-

tional (a)andfrustrated(b)

SQUID, normalized by the sin-

gle junction critical current I

as a function of the normal-

ized applied ﬂux ¥

/¥

thread-

ing through the SQUID ring,

for values of ˇ

=2 LI

/¥

0, 0.5, 1, 2, 5, 10, and 100

880 C. C. Tsuei and J.R. Kirtley

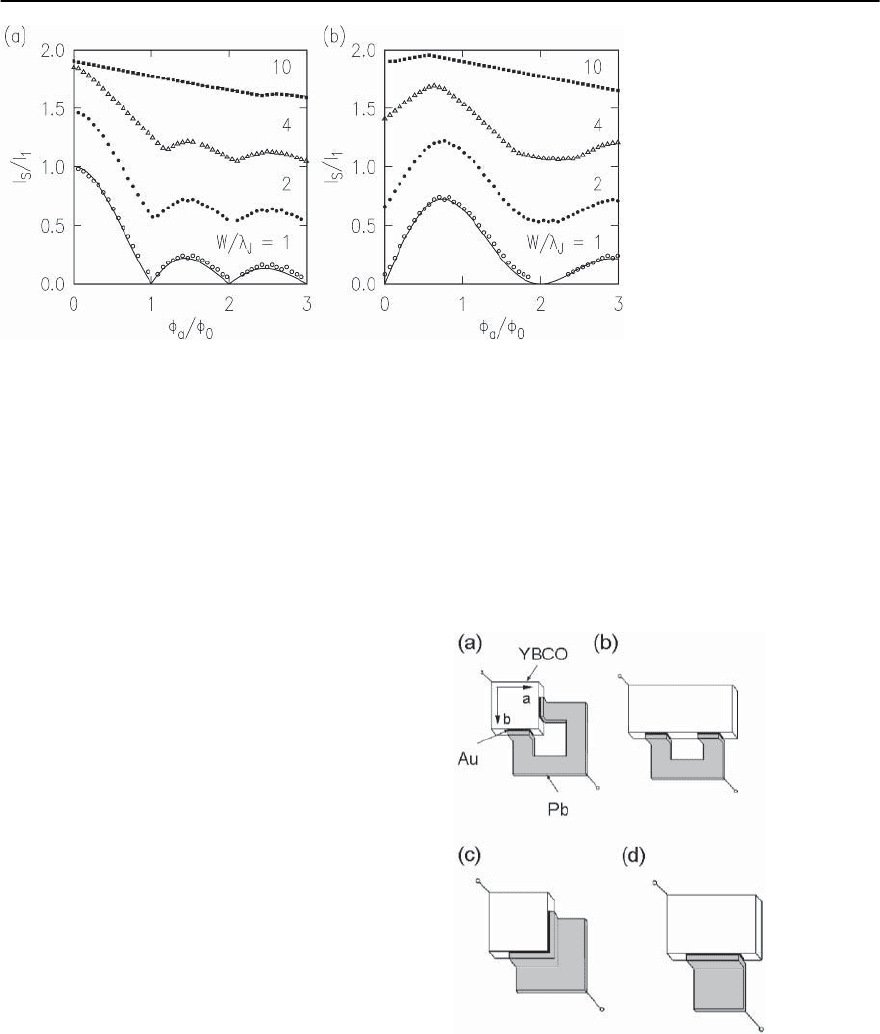
Fig. 16.7. Dependence of the total critical current I

through a single symmetric conventional (0–0, (a) and a frustrated

(0 − ,(b) junction, normalized by the single (0–0) junction critical current I

, as a function of the normalized applied

ﬂux ¥

/¥

threading through the junction, for values W /

=of0(solid lines), 1,2,4, and 10 (symbols), where W is the

junction width, and 

is the Josephson penetration depth. Each successive curve has been offset by 0.5 units for clarity

modify the interference patterns, in general further

reducing the modulation depths.

Toconcludethis section,wenotethatthere are two

ways to test for frustration in superconductingloops:

by measuring the spontaneous magnetization at zero

applied magnetic ﬂux, or by measuring the critical

current through the loop (or junction) as a function

of applied magnetic field. These two types of test are

complementary, in the sense that the spontaneous

magnetization is largest when the ring inductance or

junction width is big, but the magnetic interference

patterns are the most clear when the ring inductance

or junction width is small.

16.3 Phase-Sensitive Tests: Experiments

16.3.1 SQUID Interferometry

Wollman et al. reported the results of the first phase-

sensitive test of pairing symmetry in a controlled

configuration [104] by measuring the quantum in-

terference effects in a YBCO-Pb dc-SQUID, in the

“corner SQUID” geometry, proposed independently

by Sigrist and Rice [82]. (Fig. 16.8(a)). Josephson

weak links were made between Pb thin films and

two orthogonally oriented ac (or bc ) plane faces of

single crystals of YBCO. If YBCO is a d-wave super-

conductor, there should be a -phase shift between

weak links on adjacent faces of the crystal. Annett et

al. [5] have argued that it is plausible that the pair

transfer matrix T

k,l

(16.6) is strongly peaked in the

forward direction for both SNS and tunneling weak

Fig. 16.8. Experimental geometry used for the experiments

of Wollman et al. [104,105].(a) Corner SQUID configura-

tion, (b) edge SQUID configuration, (c) corner junction,

and (d)edgejunction

16 Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors 881

links, making the Sigrist–Rice clean relation (16.9)

applicable. Wollman et al. [104] tested for this phase

shift by measuring the SQUID critical current as a

function of ¥

, the externally applied magnetic ﬂux

through the SQUID,as described in the discussion of

Fig. 16.6. In the experiments of Wollman et al. [104],

the junction I

’s and L’s were not necessarily bal-

anced, leading to shifts in the I

vs ¥

characteristics.

Noise rounding of the current-voltage characteris-

tics of these SQUIDs made it possible for Wollman et

al. to do these measurements at several values of the

d.c. applied current through the SQUID, and correct

for these self-field effects. This was done by plotting

the phase shift as a function of d.c. current through

the SQUID, and then extrapolating to zero current

to infer the intrinsic phase shift. The intercepts for

the “corner SQUIDs” varied between 0.3 and 0.6 ¥

When these experiments were repeated with “edge

SQUIDs”,Fig.16.8(b),withtwo junctionsonthesame

ac (or bc ) face of the crystal. the intercepts centered

around zero (Fig. 16.9(a)).

There were a number of complicating factors in

the interpretation of the SQUID experimentsof Woll-

man et al. [104]. The issue of twinning will be dis-

cussed in detail in Sect. 16.3.7. Brieﬂy, if the pair or-

der parameter phase of a d-wave superconductor is

locked to the crystal axes (for example,with the pos-

itive lobe always pointing along the a direction),the

pected to alternate from twin to twin, washing out

the phase–sensitive effects described here. This does

not happen,which indicates that the d-component of

the order parameter locks across twin boundaries.

Other issues in the interpretation of these experi-

ments were the linear extrapolation in d.c. current

used [106, 107], the comparison of sample geome-

tries with corners with those without corners [108],

and the effects of ﬂux trapping.However,subsequent

phase-sensitive experiments without these problems

[87,109] have shown that these issues were not se-

rious enough to affect the qualitative conclusion of

predominantly d-wave orbital pairing symmetry in

YBCO made by Wollman et al..

BrawnerandOtt [110] performedasecondSQUID

interference experiment on single crystals of YBCO.

In contrast to the Wollman et al. experiments [104],

Fig. 16.9. Summary of the experimental results of Wollman

et al. [104,105].(a) Extrapolation of the measured SQUID

resistance minimum vs ﬂux to zero bias current for a cor-

ner SQUID and an edge SQUID on the same crystal. Each

curve represents a different cooldown of the sample. (b)

Measured critical current vs applied magnetic field for an

“edge” junction and (c) a“corner” junction

instead of using evaporated thin films for the second

electrode, they made a SQUID with two bulk point

contact junctions of niobium, producing Josephson

weak links on adjoining orthogonal faces of an un-

twinned YBCO single crystal. Two all niobium con-

trol SQUIDs on either side of the sample SQUID were

used to measure the relative phase shifts. The junc-

tion critical currents and the inductances of the two

arms of the SQUIDs were asymmetric, so that as with

the Wollman et al.[104] experiments, corrections for

self-field effects had to be made. To do this Brawner

and Ott [110] measured the dynamic resistance of

882 C. C. Tsuei and J.R. Kirtley

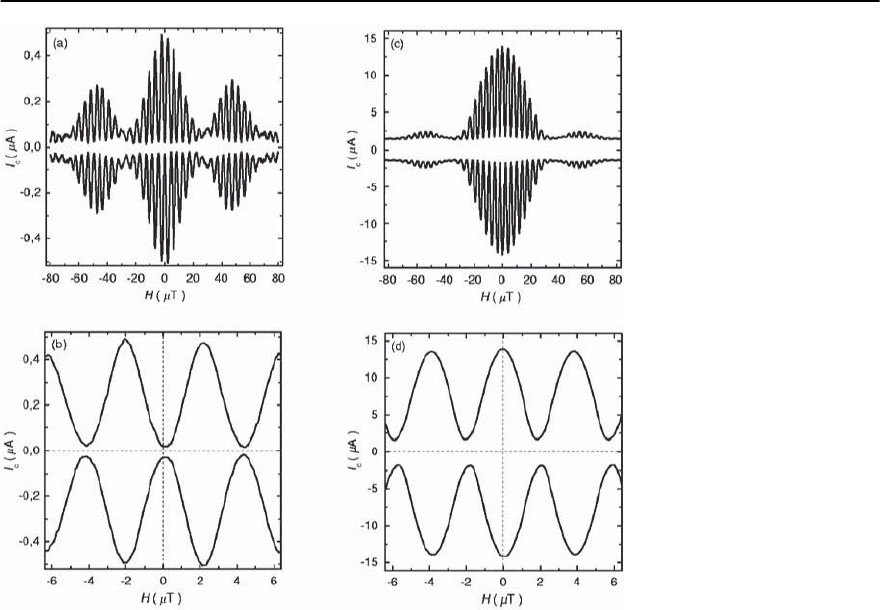
Fig. 16.10. Magnetic interfer-

ence patterns for a thin film,

spatially distributed junctions,

low inductance  -SQUID (a,

b),anda0-SQUID(c, d). The

characteristics show a nearly

ideal interference pattern over

a small field range (b, d), with

ashiftof¥

/2, as expected. An

interference envelope due to the

finite size of the junctions is ap-

parent over a larger field range

(a, c). From [109]

their SQUIDs as a function of d.c. applied current

and extrapolated their results to zero current. They

found consistent phase shifts between their control

and sample SQUIDs of 160 ±20

◦

, consistent with the

180

◦

degree phase shift expected between the normal

components to the order parameter on the two faces

of the YBCO crystal for a d

−y

superconductor.

Schulz et al. [109] produced all high-T

0and-

ring SQUIDs based on the spatially distributed junc-

tions,low inductanceSQUID design of Chesca [111],

using YBCO thin films epitaxially grown on bicrys-

tal and tetracrystal (e.g. Fig. 16.22(a)) SrTiO

sub-

strates. These devices, which had the advantages of

very small sample volumes (so that ﬂux trapping was

not an issue) and small I

L products (so that self–

field effects were negligible), showed nearly ideal de-

pendences of the critical current on applied field,

with a minimum at zero applied field for the -ring

SQUID, as expected for a d-wave superconductor in

the tetracrystal geometry used (see Fig. 16.10).

16.3.2 Single Josephson Junction Modulation

In addition to measurements in a SQUID geometry,

Wollman et al. also performed phase-sensitive mea-

surements in a single junction geometry [104, 105]

(Figs. 16.8(c) and (d)). This geometry had the ad-

vantage of being less sensitive to the effects of ﬂux

trapping and sample asymmetry. It is expected that

the critical current in the single junction geome-

try should have the interference patterns shown in

Fig. 16.7 for junctions with uniform Josephson cur-

rent density. Wollman et al. [104,105] reported con-

sistent results of a maximum in the interference pat-

tern for “edge” junctions(Fig. 16.9(b)), and a mini-

mum for “corner” junctions(Fig. 16.9(c)), consistent

with d

−y

symmetry. Similar evidence for d-wave

pairing was also reported by Iguchi and Wen [112].

As can be seen from a comparison of Figs. 16.9

and 16.7, the interference patterns reported by Woll-

man et al. [104, 104] did not agree closely with the

16 Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors 883

ideal expressions.They attributed this discrepancy to

asymmetries in the current densities in the junctions

and ﬂux trapping, and reported good agreement

with modeling including these effects [6]. However,

qualitatively similar interference patterns have been

reported for square [113] and annular [114–116]

Josephson junctions with a single vortex trapped in

them. The Illinois group reported that symmetric

interference patterns, with minima at zero applied

field, such as they observe, cannot be reproduced in

modeling with an s-wavesuperconductorin their ge-

ometry. In addition, it seems unlikely that magnetic

ﬂux consistently trappedin the Illinois“corner”junc-

tions in sucha way as to mimic d-wave superconduc-

tivity.

In an experiment analogousto the Illinois“corner”

single junction experiments, Miller et al. [117] used

frustrated thin-film tricrystal samples to probe the

pairing symmetry in YBCO. The tricrystal geometry

will be discussed in detail in the next section. Miller

et al. measured the dependence on magnetic field

of the critical current of a 3m wide micro bridge

spanning the tricrystal point. They found a mini-

mum in the critical current at zero applied field, as

expected for a d-wave superconductor in this geom-

etry, in the “short junction” limit (where the width

W of the bridge is much shorter than the Josephson

penetration depth 

[100] (seeFig.16.7).They found

that junctions in an unfrustrated geometry, or wide

junctions (L  

) in a frustrated geometry, showed

maxima in their critical currents at zero magnetic

fields [102], as expected.

16.3.3 Tricrystal Magnetometry

Controlled-Orientation Multi-Crystals

In this class of experiments, a multiple-junctionring

is made, consisting of deliberately oriented cuprate

crystals that define the direction of the pair wave-

function. The presence or absence of the half-integer

ﬂux quantum effect in such samples as a function

of the tricrystal geometry is used as an unambigu-

ous signature for a certain pairing symmetry. In the

first such phase-sensitive experiment of this type

for testing the d-wave pairing symmetry, tricrys-

tal (100) SrTiO

substrates with controlled orien-

tations were designed and fabricated (Fig. 16.11).

The c-axis oriented epitaxial cuprate films were de-

posited and photolithographically patterned into

rings (Fig. 16.12). The ring centered at the tricrystal

meetingpoint isinterruptedbythreegrainboundary

Josephson junctions.In accordance with an assumed

pair state, the three-junction ring is expected to ex-

hibit conventional integer ﬂux quantization (0-ring)

or the half-integer ﬂux quantum effect (-ring) de-

pending on the misorientation angles ˛

, ˛

,and

the angle ˇ between the grain boundaries 23 and

31 as defined in Fig. 16.11(a). For testing of d-wave

pairing symmetry, based on the Sigrist–Rice (clean)

formula (16.9), the three-junction ring is a 0-ring if

cos 2(˛

+ˇ)cos2(˛

−ˇ) is positive (with the con-

dition ˛

= /2−˛

assumed for simplicity), and

a -ring if cos2(˛

+ˇ)cos2(˛

−ˇ) is negative.In

Fig. 16.11(b), the tricrystal design parameters range

(˛

, ˇ) for -rings (which can be thought of as hav-

inganoddnumberofsignchangesintheI

’s) are

plotted as open area; and that for 0-rings (an even

number of sign changes) are shown in the shaded

areas.As emphasized in Sect.16.2.1, the effect of dis-

order at the junction interface must be considered

in the design of any viable phase-sensitive experi-

ment. It can be shown (16.10) [87] that in the max-

imum disorder limit the three-junction ring is a -

ring if cos(2˛

)cos(2˛

)cos(˛

− ˛

) is negative.

The design parameter space for the d-wave 0 and

-ring configuration with maximum disorder taken

into account is shown in Fig. 16.11(c).

The design parameters selected for the origi-

nal tricrystal phase-sensitive experiment [87] were

=30

◦

, ˛

=60

◦

,andˇ =60

◦

(Fig. 16.12), corre-

sponding to the solid dot in Figs. 16.11(b) (the clean

limit) and 16.11(c) (the dirty limit), well within the

bounds of the d-wave -ring regime. If a cuprate

under the symmetry test is indeed a d-wave super-

conductor, such tricrystal rings should show half-

integer ﬂux quantization, regardless of whether the

junction interface is in the clean or dirty limit. The

situationinanactualgrainboundaryjunctionof

cuprate superconductors is expected to fall some-

where in between. Tricrystal rings with design pa-

rameters located within the 0-ring regime (shaded

areas in Figs. 16.11(b) and 16.11(c)) should display

884 C. C. Tsuei and J.R. Kirtley

Fig. 16.11. Tricrystal geometry (a),regions of the design

parameters which give 0 (shaded a reas)and (open

areas) rings in the clean (b)anddirty(c) limits. The

• is the design point for the frustrated three-junction

ring samples (Fig. 16.16a). The ◦ (Fig. 16.16b) and ×

(Fig. 16.16c) are the design points for the unfrustrated

three-junction ring samples

Fig. 16.12. Experimental configuration for the  -ring

tricrystal experiment of Tsuei et al. [87]. The central, three-

junction ring is a  -ring, which should show half-integer

ﬂux quantization for a d

−y

2 superconductor, and the

two-junction rings and 0-junction ring are 0-rings, which

should show integer ﬂux quantization, independent of the

pairing symmetry

only the regular integer ﬂux quantization, for rings

made of a d-wave superconductor. The absence of

the half-integer ﬂux quantum effect in these three-

junction rings designed to be 0-rings represent evi-

dence for d-wave order parameter symmetry in ad-

dition to that provided by the presence of the half-

integer ﬂux quantum effect in three-junction rings

designed to be -rings.

In the tricrystal experiment of Tsuei et al. [87],

an epitaxial YBCO film (1200 Å thick) was de-

posited using laser ablation on a tricrystal (100)

SrTiO

substrate, and rings (48m inner diame-

ter, 10m in width) were patterned by a standard

ion-milling photolithographic technique. In addi-

tion to the three-junction ring located at the tricrys-

tal meeting point, two two-junction rings and one

ring with no junction were also made as controls

(see Fig. 16.12). The control rings are in the 0-ring

configuration and should exhibit the standard inte-

ger ﬂux quantization. Measurements of the critical

16 Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors 885

current densities of these grain boundaries, com-

bined with the estimated self-inductanceof the rings

L = 100 pH, indicated that the I

L product was about

100¥

, easily satisfying the condition I

L >> ¥

for

observing ¥ = ¥

/2 ﬂux quantization (see the dis-

cussion in Sect. 16.2.2).

Magnetic Flux Imaging

The magnetic ﬂux threading through the supercon-

ducting cuprate rings in the tricrystal experiments

was measured using a scanning SQUID microscope

(SSM) [118]. Themagnetic field sensor used is an in-

tegrated miniature SQUID magnetometer with sys-

tem noise about 2×10

−6

/Hz

1/2

.Shown in Fig.16.13

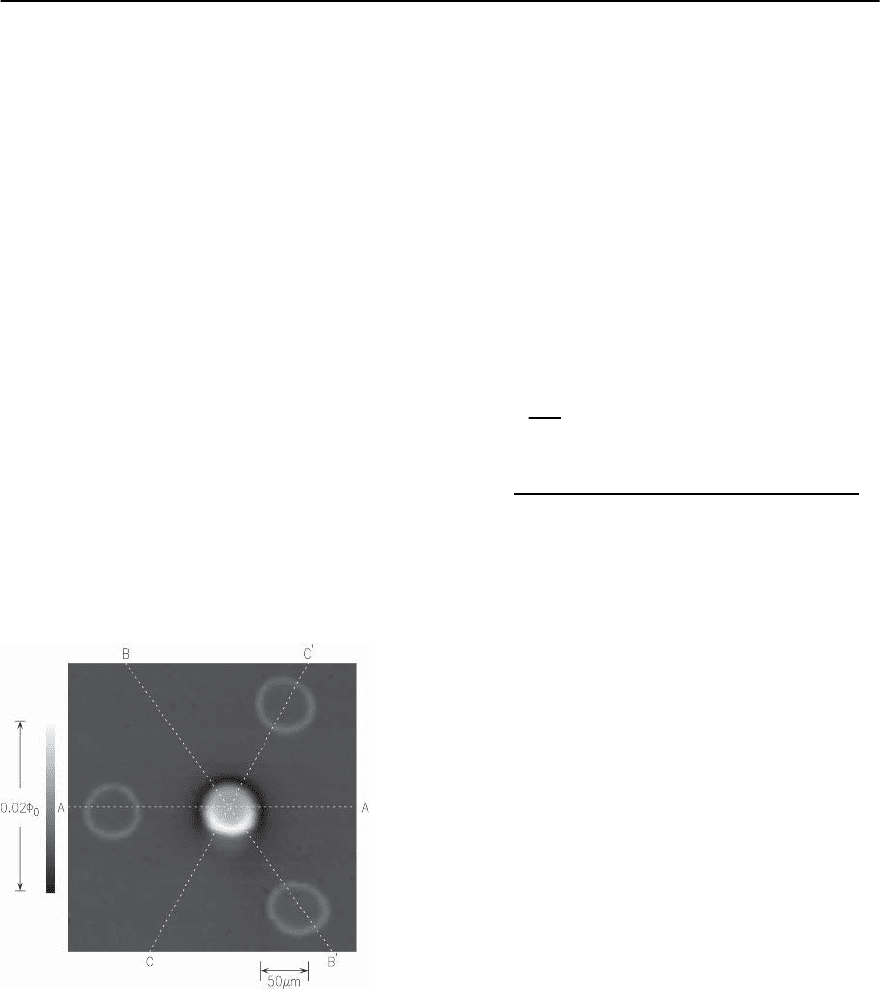
is an SSM image of four rings of c-axis oriented

epitaxial YBCO film deposited on a tricrystal (100)

SrTiO

substrate three-junction YBCO ring with the

configuration shown in Fig.16.12.As presented in the

following discussion,four different waysofanalyzing

the SSM data of the type shown in Fig.16.13 have lead

to the conclusion that the magnetic ﬂux through the

three-junction ring is indeed ¥

/2, while the other

rings contain no ﬂux, providing strong evidence for

d-wave order parameter symmetry in YBCO.

Fig. 16.13. Top view of a scanning SQUID microscope im-

age of a thin-film YBCO tricrystal ring sample, cooled and

imaged in nominally zero magnetic field. The outer con-

trol rings have no ﬂux in them; the central three-junction

ring has half of a superconducting quantum of ﬂux spon-

taneously generated in it

The four techniques for calibrating the amount

of ﬂux through the superconducting rings can be

brieﬂy summarized as follows. The details can be

found in [7].

(a) Direct calculation: A given ﬂux threading a ring

with self-inductance L induces a circulating current

= ¥

/L around the ring, which in turn produces

aﬂux¥

()=M()¥ /L in the SQUID pickup loop.

The calculated inductance of the rings of Fig. 16.13

is L =99± 5pH.

The mutual inductance M() between a pickup

loop tilted at an angle  from the sample (x − y)

plane in the x − z plane and a circular wire of radius

R at the origin can be written as:

M()=



4



dxdy

2



d (16.23)

cos (R − y sin  − x cos )−sin(z cos )

+ y

+ z

−2xR cos  −2yR sin )

3/2

where the integral dxdy is over the plane of the

pickup loop, and the vector  specifies the displace-

ment of the pickup loop with respect to the ring in

the x–y plane.

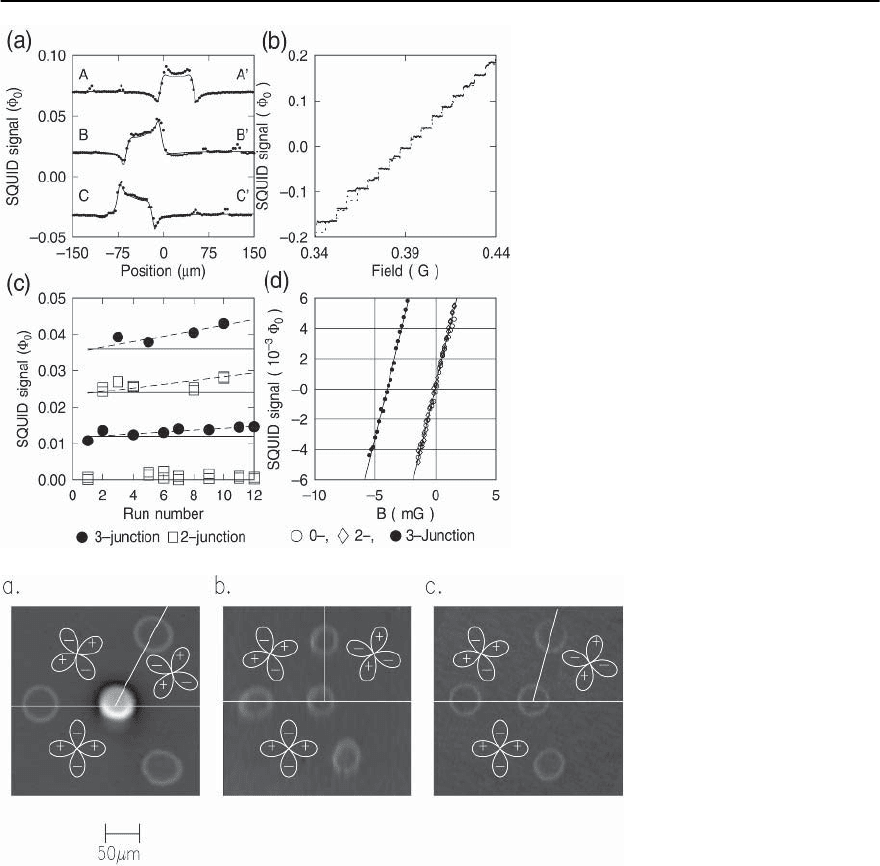
The solid lines in Fig. 16.14a are model calcula-

tions, based on (16.23) and the pickup loop geom-

etry used in the experiment, for three cross-section

through the SSM image, assuming ¥ = ¥

/2. The

asymmetry in the image can be attributed to the tilt

of the pickup loop, as well as the asymmetric pickup

area from the unshielded section of the leads. A best

fit of the SSM data yields ¥ =0.57 ± 0.1¥

,usinga

doubling of the 

as a criterion for assigning statis-

tical errors.

(b) Magnetic “oil drop”: The changes in the SQUID

signal as a function of applied magnetic field are

monitored as individual single ﬂux quanta enter the

superconducting rings. A staircase pattern in the

SQUID output vs. field thus observed (see Fig. 16.14

(b)) can be used for calibration. Using the heights of

the single ﬂux-quantum steps in Fig. 16.14(b) as a

calibration leads to values for the three-junction ring

ﬂux of 0.46 ± 0.09¥

in its lowest allowed ﬂux state.

(c)Measurements of the absolute values of the differ-

ence between the SQUID signal when the pickuploop

886 C. C. Tsuei and J.R. Kirtley

Fig. 16.14. Four techniques for demonstrating

the half-ﬂux quantum effect in the tricrystal

ring samples: (a) Direct calculation, assuming

the central ring has ¥

/2=h/4e ﬂux in it.

(b)ObservationofthechangeintheSQUID

signal as individual vortices enter the three-

junction ring, with the pickup loop centered

on the ring. (c) Measurements of the abso-

lute values of the pickup loop ﬂux when it

is directly above the 0-junction ring minus

that above the two-junction (open squar es)and

three-junction (dots)rings,foranumberof cool

downs. (d) Measurements of the SQUID signal

directly above the rings, as a function of exter-

nally applied field

Fig. 16.15. (a)–(c) Three differ-

ent SrTiO

tricrystal geome-

tries and scanning SQUID im-

ages of YBCO ring samples fab-

ricated on these substrates to

elucidate the origin of the ob-

served half-ﬂux quantum effect

in YBCO.Both the presence and

the absence of this effect rep-

resent strong evidence for a d-

wave pair state in YBCO

isdirectlyabovethe0-junction ringminusthatabove

the two-junction (open squares in Fig. 16.14(c))

and three-junction (dots) rings, for a number of

cooldowns of the tricrystal sample. The solid lines

are the expected values for the ﬂux difference, cal-

culated from (16.23) as described above. The values

of the SQUID signal always fall close to (N +1/2)¥

for the three-junction rings, and N¥

for the two-

junction rings (N an integer). The upward drift in

the data as a function of increasing run number was

due to tip wear of the SQUID assembly. The dashed

lines in Fig. 16.14(c),including this correction agree

with the data.

(d) “Magnetic field titration”: The SQUID signal at

the center of a superconducting ring, relative to the

background outside the ring, for all rings in the

experiments, can be determined by using the SSM

16 Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors 887

Fig. 16.16. Parameter space for

thepresence(open)orabsence

(shaded) of the half-integer ﬂux

quantum effect fortricrystal ge-

ometries, for an assumed sym-

metric g-wave pairing symme-

try ∼ cos k

+cosk

.Thesolid

symbol represents the design of

Fig. 16.15(a), the open symbol

is that of Fig. 16.15(b), and the

cross is that of Fig. 16.15(c)

Fig. 16.17. (a)–(c) Scanning

SQUID microscope images of

three thin film samples of

YBCO epitaxially grown on

identical d-wavetestingtricrys-

tal substrates to show the half-

ﬂux quantum effect is indepen-

dent of macroscopic sample ge-

ometry. In all cases there is a

half-ﬂux quantum of total ﬂux

spontaneously generated at the

tricrystal point, but the spa-

tial distributions of supercur-

rent are different

while varying the externally applied magnetic field

until the SQUID signal outside the ring is exactly

nullified by the screening current induced field (see

Fig.16.14(d)).The resultof such a procedure leads to

avalueof0.49±0.015¥

more ﬂux threading through

the three-junction ring that the 0-junction or two-

junction rings.

On a separate note,it shouldbe mentioned that the

reasonthatthe zero-ﬂux state of thecontrolrings(i.e.

the two-junction and 0-junction rings) are visible in

the SSM (see Fig. 16.13) is that the high sensitivity of

SSM allows it to detect very small changes in the in-

ductance of the SQUID when the pickup loop passes

over the ring, even when it contains no ﬂux.

Shown in Fig. 16.15 are the results of a series

of tricrystal experiments with various geometrical

configurations to clarify further the nature of the

observed half-ﬂux quantum effect. As expected, the

sample in panel (a),which had a frustrated geometry

fora d

−y

superconductor (˛

=30

◦

,˛

=60

◦

,ˇ =

◦

, see Fig. 16.11) showed half-integer ﬂux quanti-

zation, while the samples in panels (b) (˛

= 108.4

◦

=71.6

◦

, ˇ =90

◦

) and (c) (˛

= 107

◦

, ˛

=73

◦

ˇ =75

◦

) [119,120] which had 0-ring configurations

(i.e. shaded areas in Figs. 16.11(b) and 16.11(c)), did

not. The absence of the half-integer ﬂux quantum

effect in these two tricrystal experiments has ruled

outany symmetry-independent mechanisms [89,90]

as the cause of the -phase shift. In addition, the

tricrystal shown in panel (c) rules out even-parity g-

wave pairing symmetry with order parameter vary-

ing as (cos k

+cosk

) (see Fig. 16.16).

As concluded from the discussion in Sect. 16.2.2,

half-integer ﬂux quantization is a manifestation of

the ground state in any singly connected supercon-

ducted loop with an intrinsic phase shift of .The

observation of such an effect should be independent

of the macroscopic form that the sample takes. In-