Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

838 J.Zasadzinski

though only half of the series resistance for quasipar-

ticle excitations is present, and thus the conductance

is doubled. This occurs only for voltages such that

eV < . For voltages beyond this value quasiparti-

cles are transmitted directly into the superconduc-

tor and there is an abrupt decrease of conductance

back to the normal state conductance of the two elec-

trodes. Thus the pure metallic SN contact provides a

measure of the“coherent”gap associated with super-

conductivity.

For Z > 1 the tunneling regime develops and the

standard SIN quasiparticle gap feature is observed.It

is thereforeuseful to explore both regimes with point

contacts. Quasiparticle excitation gaps observed in

tunneling can arise from a variety of sources includ-

ing charge or spin density waves (CDW or SDW)

as well as from superconductivity. But the Andreev

process described here only occurs for the phase co-

herent superconducting state.

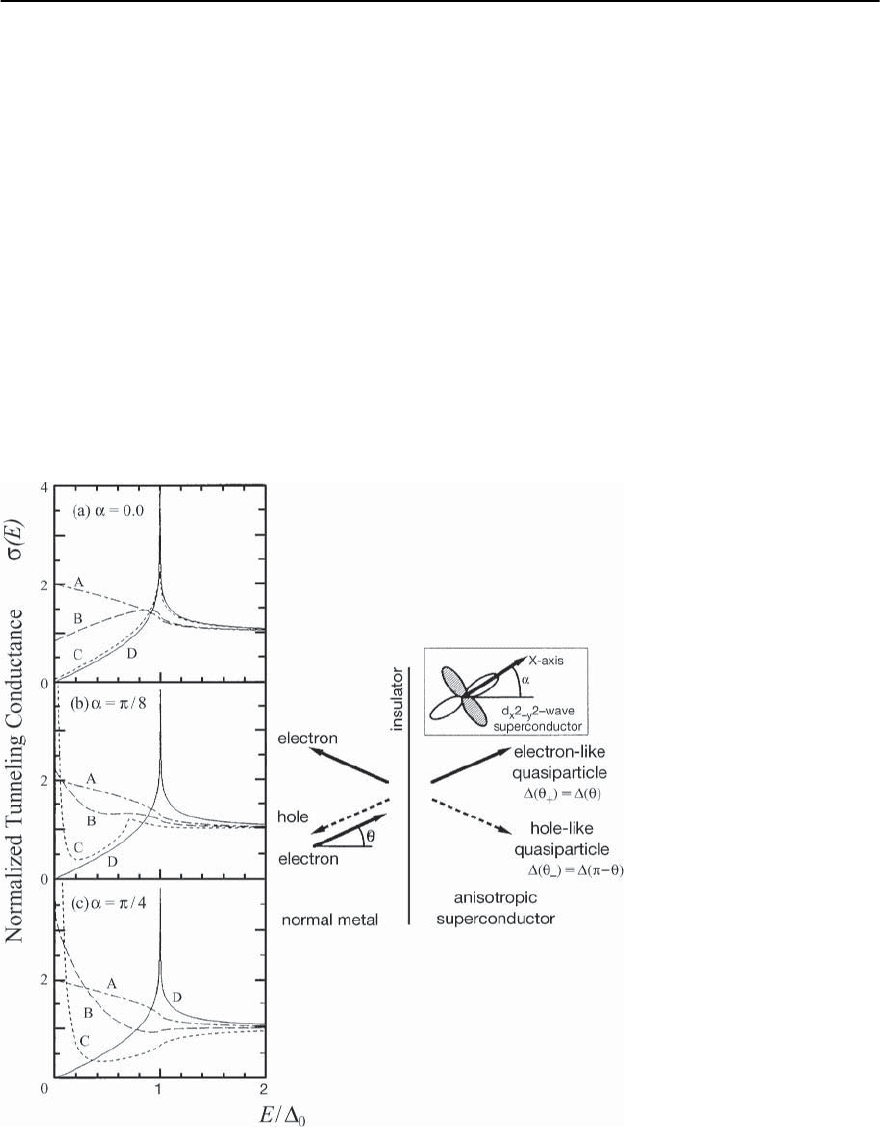
15.2.4 Novel d-Wave Effects

The BTK model has been extended to d-wave super-

conductors. In particular, novel effects are found for

junctions where the barrier plane is perpendicular to

the ab plane of cuprates. An example of this type of

junction is shown schematically in Fig. 15.1(d). This

is due to the fact that the quasiparticles in the ab

plane which undergo a specular reﬂection from the

superconductor/insulator interface may experience

a sign change of the order parameter. For example,

the scattering is from − to + and therefore the

formalism which describes such a reﬂection is sim-

ilar to that of the proximity effect interface in S/N

bilayers, described later. The general consequence of

Fig. 15.6. Right:schematicof

the tunneling geometry for ab

plane junctions. Left:calcula-

tions of the junction conduc-

tances for various angles ˛

and barrier strengths Z,from

Tanaka and Kashiwaya [16]

15 Tunneling Spectroscopy 839

such scattering events is the development of Andreev

boundstatesinthequasiparticleexcitationspectrum

at the Fermi energy. These bound states exist only at

the interface but nevertheless can have important ef-

fects on the measured tunneling spectrum, leading

to a zero bias conductance peak (ZBCP) in certain

geometries. These effects for d-wave superconduc-

tors were first discussed by C.R. Hu [15] and later

developed within a generalized BTK framework by

Tanaka and Kashiwaya [16].

Thed-waveBTK model is shown in Fig.15.6 where

the right panel indicates the geometry considered.

The angle ˛ is between the barrier normal and the

lobe direction of the d-wave order parameter. Con-

sider first the curves labeled A in the left panel of

Fig. 15.6 which correspond to Z =0.Thesecurves

represent the d-wave analogue of the Andreev re-

ﬂection curve in Fig. 15.5 and display a less abrupt

decrease of the conductance near eV =  compared

to the s-wavecasewhichisduetothegapnodes.

There is no ˛ dependence to the Z =0curvesbe-

cause all incident quasiparticles are assumed to have

equivalent transmission probabilities. The effect of

a tunnel barrier is seen in the curves labeled C. For

non-zero values of ˛ a sharp peak at zero bias is ob-

served and the coherence peaks at the gap voltage are

diminished considerably. Spectral weight in the DOS

has been shifted from the coherence peaks to the An-

dreev bound states which produce the ZBCP. There

is no ZBCP for c-axis tunnel junctions (Fig. 15.1(e))

because the barrier is parallel to the ab plane and

specular reﬂections off the interface have no effect

on in-plane wavevector and thus no sign change oc-

curs. It thus turns out that c-axis tunnel junctions

are the only ones capable of revealing the intrinsic

quasiparticle DOS.

15.2.5 Strong- Coupling Effects: Phonon Structure

For s-wave superconductors the extension of

Eq. (15.2) to the strong-coupling limit has been

worked out in Migdal–Eliashberg theory. [1] The su-

perconducting part of the DOS is given by

 (E)=Re

|E|



− 

(E)

, (15.5)

where now it is understood that (E)isacomplex

function of the quasiparticle energy, E, in the super-

conducting state. The imaginary part is related to the

finite lifetime of the quasiparticle due to emission of

phonons and thus becomes largest near peaks in the

phonon density of states. This gives rise to struc-

tures in  (V) as shown in Fig. 15.7 for PCT junction

on single crystal Nb. [17] There are several notewor-

thy points to be made here. First, the normal state

conductance, often referred to as the background

conductance, is rather featureless, showing a weak,

Fig. 15.7. Tunneling conductance of Nb in the

superconducting andnormal states obtained by

PCT in the region of phonon structures, from

Huang et al. [17]. Peaks in ˛

F(!)(inset)give

rise to dip structures in the superconducting

state dynamic conductance

840 J.Zasadzinski

parabolic increase which is due to the barrier.Second,

the superconducting conductance near the phonon

structures is less than the normal state by about 1.5

percent. This leads to a dip in the normalized con-

ductance or superconducting DOS. Physically this

means that states have been lost in this region due to

phonon emission and have been transferred primar-

ily to lower energies leading to a pile-up at the gap

edge. This effect provides a straightforward means

of identifying strong coupling effects. Inversion of

the normalized conductance using the MR proce-

dure [1, 2], leads to ˛

F(!)shownintheinsetof

Fig. 15.7. The dip minima in  (V) are close to the

peaks in ˛

F(!), but more precisely it is the maxima

of the second derivative,

d(V)

,that correspond to the

peaks.

15.2.6 I nelastic Tunneling

Until now the only conductancechannel assumed for

the junction was elastic tunneling where initial and

final state energies are the same. However, transport

across a junction can occur by other means such as

inelastic tunneling [1,18],orresonanttunneling [19].

Resonant tunneling is a multistep process whereby

the electron first tunnels to a bound orbital state of

an impurity atom or ion in the tunnel barrier and

then tunnels again into the other electrode. This can

be elastic or inelastic and may involve more than one

intermediate steps. Resonant tunneling will not be

discussed since it tends to wash out the quasipar-

ticle DOS and the resulting spectra are indicative of

the barrier states.On the other hand, the spectra pre-

sentedhereare clearly associatedwiththe gap feature

in the DOS of the superconducting electrode since

they disappear above T

. However, the resonant tun-

neling process is believed to be playing an important

role in grain-boundary junctions on cuprates [20].

Of more relevance to the issues of concern here

is inelastic tunneling. With this channel it is as-

sumed that the electron undergoes either absorption

or emission of an excitation of energy ! simulta-

neously with tunneling through the barrier. At liq-

uid helium temperatures, the emission process dom-

inates,andthis occursata thresholdvoltage eV = !

when the tunneling electron has sufficient energy

to create the excitation. At this voltage the inelastic

conductance channel opens up and there is a step

increase in the conductance. For a ﬂat continuum of

excitations the sum of such steps leads to a linear

increase in conductance [21].

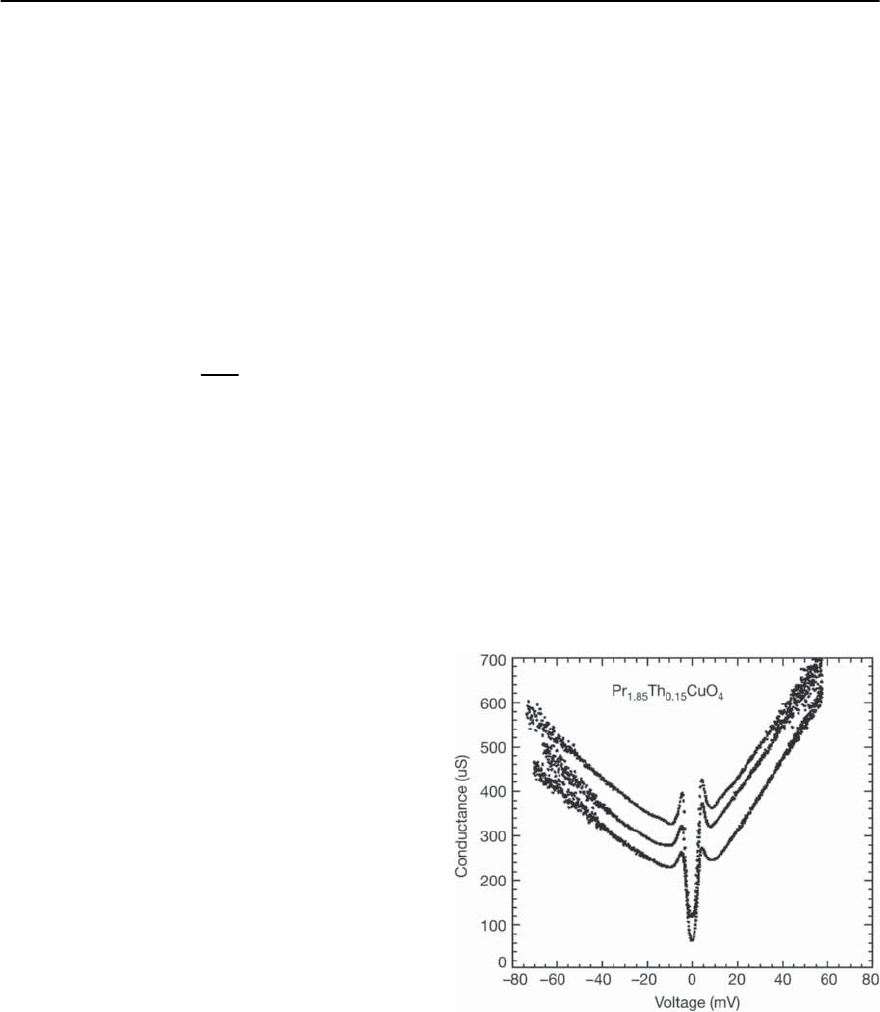
Strong linear increases in background conduc-

tance were often seen in the early tunneling lit-

erature on cuprate and bismuthate superconduc-

tors [22]. An example of this effect is seen in

Fig. 15.8 for Pr

1.85

0.85

CuO

which is similar to

the linear backgrounds observed in other electron

doped cuprates [23]. The V-shaped background ex-

hibits an increase in conductance of 100% or more

at 60 mV compared to the extrapolated value at

zero bias. This should be compared to the ordinary

parabolic shaped background for elastic tunneling

in Nb shown in Fig. 15.7. In that case the increase at

60 mV is only about 10% and is due to the barrier

effect from the Nb-oxide layer. For Al-Al oxide-Pb

junctions the increase would be about 2%. Thus it is

clear the strong V-shaped background is not a con-

sequence of ordinary barrier effects.

There was early speculation that the linear tunnel-

ingbackgroundmightbeintrinsicinoxidesupercon-

ductors,owingpossibly to the Marginal Fermi Liquid

Fig. 15.8. Measured conductances of three different

point contact tunnel junctions on a polycrystal of

1.85

0.85

CuO

from the Argonne group (unpublished).

Similar strong linear increases are observed in other

electron-doped cuprates as seen in [23]

15 Tunneling Spectroscopy 841

behavior of the quasiparticle self-energy evident in

many experiments on optimal doped cuprates. How-

ever, such self-energy effects do not lead directly to

linear increases in the total electronic DOS, N(E),

abouttheFermienergy.Furthermore,Kirtleyshowed

that such an inelastic channel was easily induced in

ordinary tunnel barriers by introducing magnetic

impurities into the oxide [24]. The incoherent spin

ﬂuctuationsof the weakly coupled spins gave the ﬂat

continuum of excitations. Further evidence that the

linear background is due to an additional channel

can be found by considering the ratio of the con-

ductance peak height to background (PHB) which is

typically a value of 2 or more for high quality SIN

junctions (e.g. see Figs. 15.2 and 15.4). When strong

V-shaped backgrounds are observed the PHB ratio is

significantly smaller than 2 ascanbe seen in Fig.15.8.

This seems to be a general result.

15.3 Tunneling and Strong-Coupling Effects:

Microscopic Picture

Here we provide a more detailed theoretical treat-

ment of the tunneling process and examine the var-

ious approximations that go into the expression for

the tunnel current. We follow the transfer Hamilto-

nian approach of Bardeen [25]. The total Hamilto-

nian for the system is

H = H

+ H

, (15.6)

where H

and H

are the Hamiltonians for the left and

right metalsin theabsence of tunneling.Theperturb-

ing Hamiltonian H

for the weak virtual coupling is

given by



k,q

bfk,q

†

+ c

†

}, (15.7)

where c

†

, c

†

and c

are creation and annihila-

tion operators for quasiparticles in the eigen states

and '

of the left and right metals, respectively.

The tunneling matrix element



k,q



was obtained

by Harrison [26] as



k,q



4

k

q



k⊥



q⊥

exp[−2



⊥

(z)dz] , (15.8)

where 

⊥

=(L/)dk

⊥

/d

⊥

is the one-dimensional

band structure density of states (proportional to the

inverse of the group velocity normal to the barrier)

and L is the length of the metal in the normal direc-

tion to the oxide surface. The group velocity nor-

mal to the barrier enters because the tunnel cur-

rent is a rate of charge transfer which necessarily

involves an attempt frequency of electrons on the

tunnel barrier. Here K

⊥

(z)=



2m['(z)−E

]/

= E − 

+ k

)/2m is the kinetic energy of the

electron in the z-direction (normal to interface), and

'(z) is the barrier potential.Here E is measured from

the bottom of the conduction band.

Due to the exponential dependence on the normal

component of energy, the tunneling matrix element

heavily weights the contributions of electrons nor-

mal to the barrier.There is also a voltage dependence

to the matrix element as the shape of the barrier

changes with V , e.g. an initially rectangular barrier

becomes trapezoidal with applied voltage.For values

of eV  (z) this barrier effect is negligible and the

tunneling conductance for two normal metal elec-

trodes in nearly constant. However, as the applied

voltage becomes a reasonable fraction of the barrier

height, a parabolic term is added to the background

conductance, [27] an effect which can be observed in

Fig.15.7 since the barrierheight of Nb oxide is about

250 meV [17].

The standard Fermi’s Golden Rule for the tran-

sition rate !

r←l

from an initial state i on the left

metal to a final state f of equal energy on right metal

can be obtained by substituting Eq. (15.7) into the

time-dependent Schr¨odinger equation. Subtracting

the rate from right to left leads to the following form

for the tunnel current

I =2e



∞



−∞

2

(k, !)A

(q, ! + eV)

× [f (!)−f (! + eV)] .

This form for the tunnelcurrentisparticularly useful

for it incorporates the quasiparticle spectral weight

function

A(k, !)=



Z! + "

− (k)

]−"



, (15.9)

842 J.Zasadzinski

a quantity that is measured directly in angle-resolved

photoemission spectroscopy (ARPES). The spectral

weight contains all information about electron cor-

relation effects via the renormalization parameter,

Z(k, E) and gap parameter, (k, E). The general

problem of a momentum dependent pairing inter-

action leading to a strong-coupled d-wave supercon-

ductor has not been solved self-consistently as with

Migdal–Eliashberg theory for s-wave superconduc-

tors. Consequently, calculations of A(k, !) usually

involvesometypeofapproximationscheme.The

connection to the quasiparticle DOS is given by

N(!)=



A(k, !) ,

which can be measured in tunneling. The simplest

case scenario is to assume the tunneling matrix el-

ement is a constant, independent of energy, voltage

and momentum, and can be taken out of the sum-

mation. Performing the sum over momenta leads

directly to Eq. (15.1), with N(!)correspondingto

the full, three dimensional quasiparticle DOS in-

cluding band structure and correlation effects. How-

ever,this scenario is unrealistic. The matrix element

of Eq. (15.8) is clearly not constant and heavily

weights quasiparticle momenta normal to the bar-

rier. If both electrodes are assumed to be nearly free

electron metals with ellipsoidal Fermi surfaces, then

the dominance of contributions to the tunnel cur-

rent from near-normal incident quasiparticles leads

to a collapse of the transverse momentum sum in

Eq. (15.9). The resulting momentum sum is over k

⊥

and q

⊥

which gives the one-dimensional band struc-

ture DOS and this is canceled exactly by the group

velocity term in the matrix element. For supercon-

ducting electrodes, the resulting expression is identi-

cal to Eq. (15.1),but with the superconducting DOS,

 (E) used instead of N(E). This cancelation by the

group velocity, first pointed out by Harrison, leads to

the commonly held viewthat tunneling spectroscopy

does not probe band structure effects. However, this

is a consequence of several contributing factors, and

is not necessarily true in general.

Cuprate superconductors are composed of inco-

herently coupled Cu-O layers, giving rise to a quasi

two-dimensional system and Fermi surface. Even as-

suming some weak coherent coupling which would

give rise to dispersion along the c-direction, the re-

sulting Fermi surface would have open faces perpen-

dicular to the k

-direction. For STM or point con-

tact configurations where the tip is pointing along

the c-axis of cuprate superconductors there can be

no tunneling of electrons with momenta normal to

the barrier as there are no such states on the Fermi

surface. Thus it is expected that the tunneling cur-

rent from tip to sample in an STM junction or from

Cu-O plane to Cu-O plane in an intrinsic junction is

made up of electrons with momenta transverse to the

barrier.This is quite different from conventional su-

perconducting metals discussed earlier and the key

result is that there is no cancelation of band structure

effects from the group velocity normal to the barrier.

The resulting N(E) should be the 2D density of states

in the Cu-O plane including band structure effects.

Oneofthedominantfeaturesofthebandstruc-

ture is the extended saddle point near the (, 0) di-

rection which gives rise to a peak, or van Hove sin-

gularity (VHS), in the DOS [28]. Tunneling data out

to very high bias voltages has provided some evi-

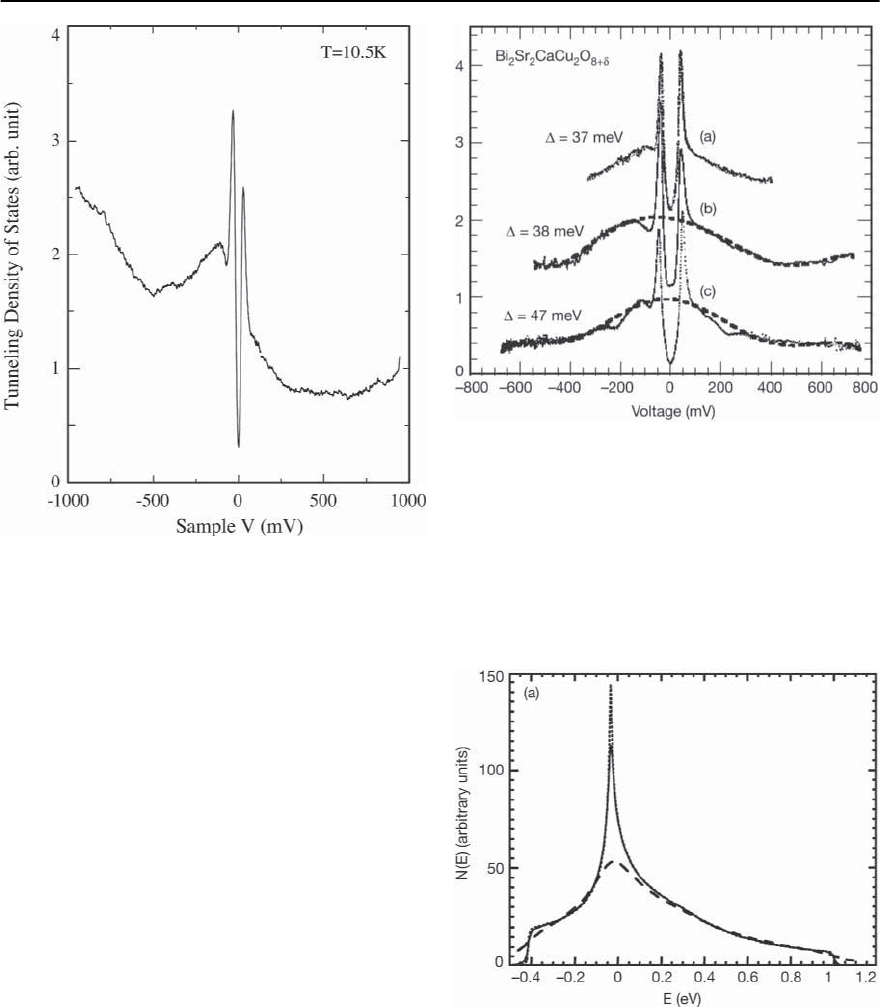
dence for this feature as shown in Fig. 15.9 which is

an STM tunneling conductance on a cleaved surface

of Bi2212 [29]. In addition to an asymmetric back-

ground there appears to be a broad peak in the con-

ductance centered near zero bias. It is difficult to lo-

cate the VHS peak because the superconducting gap

feature (including dip structures) is emerging out of

this background. This broad peak has a width of at

least 800 meV which is consistent with the expected

bandwidth.

A similar broad peak is found in PCT conduc-

tances of Bi2212 measured by the Argonne tunneling

group (including some unpublished spectra, see, for

example, [30]). These are shown in Fig. 15.10 where

spectra from three different crystalswith slightly dif-

ferent oxygen dopings are presented. Again a broad

peak with a characteristic width of about 800 meV

can be inferred from the data. Yusof et al. have used

the fits of ARPES data to generate the band struc-

ture DOS for Bi2212 and this is shown in Fig. 15.11

for three different values of the quasiparticle scatter-

ing rate [31]. It is not clear what value of  should

be used. Above T

the ARPES spectral weight peak

15 Tunneling Spectroscopy 843

Fig. 15.9. STM spectra of superconducting Bi2212 out to

high bias voltage. From Sugita et al. [29]

is considerably broadened, but is resolution limited

in the superconducting state. From observation of

Fig. 15.9 and Fig. 15.10 it appears that a  value near

thesuperconducting gapenergy would provide a rea-

sonable fit to the measured high bias spectra.

Thus it appears that the decreasing background

conductance that is commonly observed in the tun-

neling conductances of hole-doped cuprates is due

to the underlying band structure DOS. However, the

VHS peak itself is never directly observed and this is

probably due to the fact that it is pinned somewhere

close to the Fermi energy and is thus inside the su-

perconducting gap. From the fits to the ARPES data

on near optimal doped Bi2212, the peak in the band

structure (b.s.) DOS is found about 30 meV below

the Fermi energy so this is consistent with such a fea-

ture getting masked when a superconducting gap of

 = 35 meV develops in the superconducting state.

Above T

the scattering rate is increased consider-

ably and there might exist a pseudogap, both effects

tending to obscure the observation of the VHS.

Fig. 15.10. High bias PCT spectra of superconducting

Bi2212, obtained from three different crystals. (a) and (b)

correspond to optimally doped and (c) is from an under-

doped crystal. Dashed lines through (b) and (c) are sixth

order polynomial fits through the data

Fig. 15.11. Band structure density of states of Bi2212 as ob-

tained from fitting ARPES spectra, from [31]. The different

curves correspond to different values of the quasiparticle

scattering rate, .Thedotted, solid and dashed lines corre-

spond to  =3,8,80meV,respectively

844 J.Zasadzinski

15.4 Tunneling Spectroscopy

of Conventional Superconductors

In the previous sectionthe basic formalism for elastic

tunneling was presented.For conventional supercon-

ductors with closed Fermi surfaces the tunnel cur-

rent in SIN junctionsis dominated by electrons with

momenta normal to the barrier. Consequently the

band structure DOS is canceled by the group veloc-

ity and only the superconducting part,  (E), rescaled

by a constant enters Eq. (15.2). This technical point

is generally ignored for conventional superconduc-

tors, but as was shown in the previous section the

role of band structure effects can be quite important

for understanding the tunneling spectra of cuprate

superconductors.

Since most conventional superconductors, espe-

cially s-p metals and alloys, have a weak energy de-

pendence of the b.s.DOS near the Fermi energy,then

even if the N(E) was the full DOS, the band struc-

ture part would be expected to be nearly constant

over the voltage range of interest (approximately 50

meV). Normalization of the tunneling data would be

expected to give (E) as before, giving an implicit

measure of (E) via Eq. (15.5). An example of such

data for ZrN,and the corresponding analysis,is given

below.

Before proceeding it is reasonable to ask whether

there is any evidence that the tunnel current in con-

ventional superconductors is dominated by electrons

normal to the barrier. Noteworthy here is the fact

that planar junctions on single crystals of Nb ex-

hibit reproducibly different ˛

F(!) for junctions

fabricated on (100),(110) and (111) crystallographic

planes. This is perhaps the most direct evidence for

tunneling directionality effects [1]. Also, junctions

on (N/S) bilayers are consistent with proximity effect

models which assume specular tunneling normal to

the barrier. This is discussed later.

15.4.1 McMillan–Rowell Analysis

Thereisanexhaustiveliteratureonconventional,

lower T

superconductors,detailing how the complex

gap parameter, (E), can be inverted using Migdal–

Eliashberg theory [1] to obtain the microscopic inter-

actions responsible for superconductivity. The pro-

cedure of McMillan and Rowell (MR) [2] is iterative,

beginning with an educated guess for the electron–

phonon spectral function,˛

F(!)andtherenormal-

ized coulombpseudopotential,

∗

.These parameters

arethenrefined by comparisonof the calculated (E)

with the measured normalized conductance. We will

not review the early works but rather show some

relatively recent data on the binary compound, ZrN,

which has a T

of 9.4 K and is exemplary of the MR

analysis [32].This material is also of interest because

it exhibits relatively high frequency optical phonon

modes and the issues concerning whether and how

electrons couple to such modes is of great interest.

ZrN is one member of a class of transition metal com-

pounds with the NaCl structure such as NbN, NbC,

and HfN. These materials have excellent mechani-

cal properties as well as superconducting transition

temperatures as high as 18 K.

Thin films of ZrN were prepared by reactive sput-

tering and then oxidized in laboratory air for 50

h to form the tunnel barrier. The planar junction

was completed by evaporation of an In counterelec-

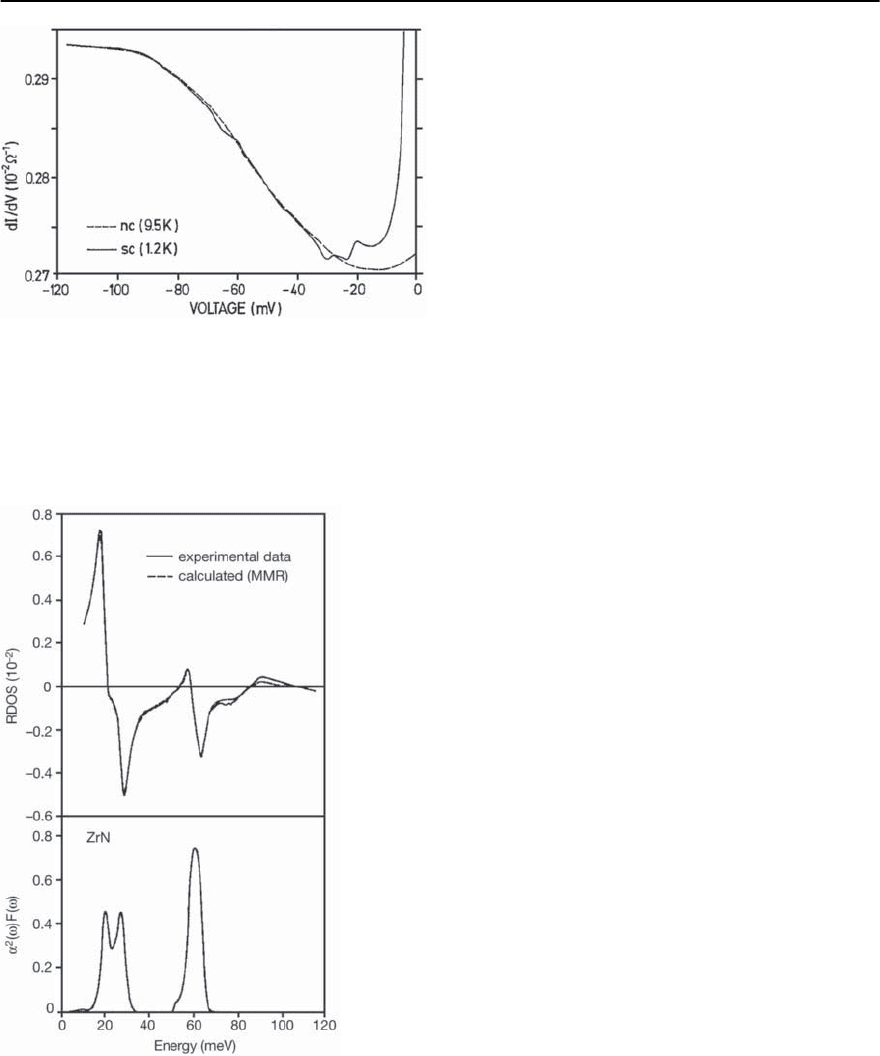
trode. In Fig. 15.12 is shown the dynamic conduc-

tance

vs. V in the superconducting and normal

state.Acoustic mode phonon structuresare observed

in the range 20-30 mV and a distinct dip feature is

found near 60 mV which is in the range of opti-

cal phonons. Note that these phonon structures in

the superconducting state conductance lie below the

normal state curve and this is a critical feature of

strong coupling effects, arising from the imaginary

part of the gap function (E) and reﬂecting a loss of

states in this region. Had this feature been due to an

inelastic channel opening up there would be an in-

crease of conductance in both the superconducting

and normal state spectrum.

In Fig. 15.13 is shown the reduced conductance

(

(V)



BCS

-1) and the fit obtained from the MR inversion

analysis. Also shown is the resulting ˛

F(!)spec-

trum which is found to be in very good agreement

with the phonon density of states F(!)measured

by inelastic neutron scattering. The coulomb pseu-

dopotential 

∗

= 0.1 is in the expected range and

the calculated T

=8.4 K is reasonably close to the

experimental value. This experiment provides clear-

15 Tunneling Spectroscopy 845

Fig. 15.12. Superconducting (solid line) and normal state

(dashed line) conductance for planar junction, ZrN/ZrN-

oxide/In. The superconductivity of In has been quenched

with a small magnetic field

Fig. 15.13.Top p anel : measured and calculated reduced con-

ductance. Bottom panel: the resulting ˛

F(!)fromMR

inversion

cut evidence for electron coupling to high frequency

optical modes. It is for this reason that such a rela-

tively high-T

couldbeobtainedwitharathermod-

erate coupling strength =0.62. It is thus clear that

for oxide superconductors, which have even higher

frequency optical phonon modes,the possible role of

electron–phonon coupling must be considered.

15.4.2 Proximity Effect Tunneling in Conventional

Superconductors

Tunneling investigations of (N/S) bilayers has had

a tremendous impact on the field of conventional

superconductivity from both a fundamental and ap-

plied perspective.Such studies have provided a more

complete understanding of the electron–phonon in-

teraction (even in non-superconducting elements

such as Mg) and have generated numerous electronic

devices, such as high-speed A/D converters and sen-

sitive photon detectors. A brief discussion of this

area is therefore warranted. Furthermore, the field

is mature and well understood so that speculations

about proximity effects in unconventional supercon-

ductors such as high-T

cuprates can be critically

examined using this information base.

We imagine here junctions of the form C-I-NS

where C is a convenient counterelectrode, either a

normal metal forspectroscopy studies of the N and S

layer, or a superconductor for studies of the Joseph-

son effect and related device phenomena. Thus tun-

neling is into (or out of) the N side of the normal

metal/superconductor sandwich as shown schemat-

ically in the inset of Fig. 15.14. By using N lay-

ers of known thickness and properties, such struc-

tures have extended the standard tunneling spec-

troscopy and MR inversion procedure to include

superconducting elements, alloys and compounds

which themselves do not form suitable surface ox-

ides for tunnel barriers or which are strongly affected

by proximity to non-native oxides, such as from the

counterelectrode [1,33].

Simple examples are Nb and V whose native sur-

face oxides are complex, consisting of various oxide

phases (including e.g. NbO which is metallic). These

complex oxides also have defects, e.g. voids or ion-

ized atoms, which increase the likelihood of mul-

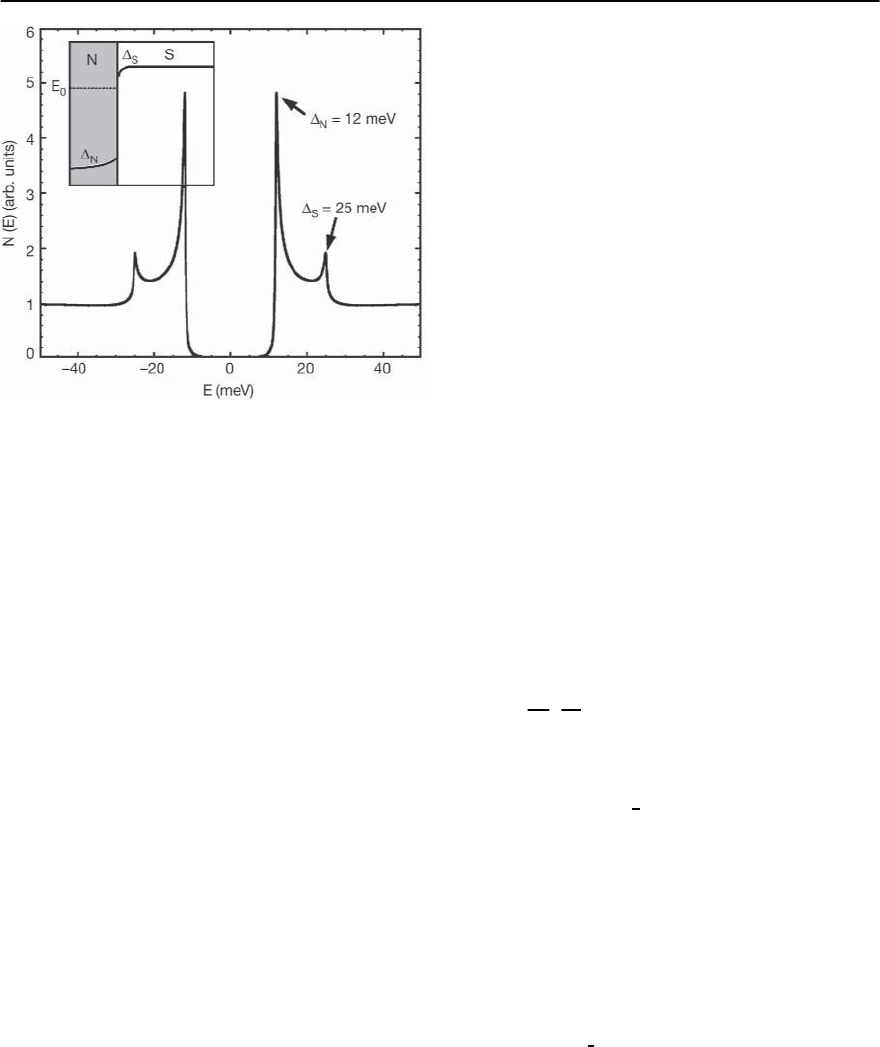
846 J.Zasadzinski

Fig. 15.14. McMillan model for the density of states N

(E)

obtained for tunneling into the N side of an NS bilayer.In-

set: schematic representation of the superconducting gap

parameters in the proximity sandwich

tistep, resonant tunneling processes which compete

with the desired direct elastic tunneling between the

two metal electrodes. [34] In addition, even small

amounts of diffused oxygen are known to rapidly

decrease the superconducting T

of Nb and V (ap-

proximately 1 K per atomic percent of oxygen) which

means the standard fabrication method of evaporat-

ing or sputtering Nb or V onto oxidized films of Al

does not work. The resulting gap region characteris-

tics are extremely broadened and all phonon struc-

tures are smeared out, most likely due to the fact that

the resulting junction is of the form Al/Al-oxide/S’S

where S’ is an inhomogeneous, disordered layer of

reduced superconductivityon the surface of the bulk

superconductor of interest.

To circumvent such problems, a new method was

developed during the mid 1970sknown as proximity

electron tunneling spectroscopy (PETS) [35], which

allowed a quantitative fit to the tunneling spectra

of N/S bilayers using the proximity effect theory of

Arnold.The two relevant models for proximity effect

tunneling are those of McMillan and Arnold which

we discuss brieﬂy. The McMillan model assumes the

N/S interface has a weak, delta function barrier for

diffuse tunneling to occur, allowing a perturbation

treatment of the problem. The calculation generates

a set of coupled non-linear equations which deter-

mine the gap functions,

(E) in the S layer (reduced

from itsbulk value) and

(E) induced in the normal

layer.The quasiparticle density of states in each layer

is that given by Eq. (15.5) but with the appropriate

gap parameter.Assuming the N layer has no intrinsic

pairing interaction and is much thinner than S, then

the McMillan DOS in the N layer is determined by

two parameters, the bulk superconducting gap and a

scattering rate,

, which is inversely proportional to

the N layer thickness.

An example of the expected tunneling density of

states in the normal metal from the McMillan model

is shown in Fig. 15.14 assuming a superconductor

with a bulk gap of 25 meV, a value typical for high-T

cuprates.While the McMillan model has intuitiveap-

peal for understanding the proximity effect attempts

to extract ˛

F(!) in either the N or S layer were un-

successful [33].The PETS method utilizes a clean N/S

interface and this is described by the Arnold model,

which, in the limit of small N-layer thickness, allows

a direct measure of the underlying S-layer gap func-

tion [33]. The specular N/S interface also results in

resonance effects due to Andreev reﬂection, and this

leads to quasiparticle bound states in the N layer as

well as higher energy oscillations of the DOS. The

relevant parameter which determines these effects

is R =(

1+r

1−r

)

.Herer is the reﬂection coefficient

between N and S layers due to differences in Fermi

momenta,v

is the fermi velocityin the N layer and d

is the N-layer thickness. The first bound state energy

is given by,E

=

(1−

(R

),and is shown schemat-

ically in Fig. 15.14. An example of the DOS for very

thick N layers is shown in Fig.15.15 where the bound

states and oscillations are clearly visible.

Of more relevance to the issue of pairing interac-

tions is the Arnold model in the ultra thin N layer

limit, i.e. R ≈ 0. In this case it can be shown that

phonon structures from the underlying S layer as

embedded in 

(E) can be observed as if tunneling

directly into S, but with a reduced amplitude scaled

by the factor e

−

. Thus the standard MR inversion

procedure can be used but modified to include an

additional free parameter, d/l,wherel is a quasipar-

ticle mean-free-path in the N layer. This is referred

15 Tunneling Spectroscopy 847

Fig. 15.15. Arnold density of states for relatively large R

values. Note the presence of two bound states for R =0.2

to as the modified McMillan–Rowell or MMR proce-

dure.

From the experimental side the idea was to form a

nearly perfect N/Sinterface by depositing a thin layer

of Al onto a clean single crystal superconductor, such

as Nb, in an ultra-high vacuum environment. The Al

layer was known to provide an ideal, self-limiting

oxide tunnel barrier and at the same time the unoxi-

dizedportionwouldprovideaprotectivelayerforthe

superconductor.The first successful junctions of this

type on Nb and V showing clear phonon structures

were published in 1978 [35] and a full quantitative

analysis using theArnold proximity effect model ap-

peared a few years later [36,37].These results showed

that the standard MR inversion procedure could be

extended to (N/S) bilayers allowing a determination

of ˛

F(!) in transitionmetals such as Nb andV. Ex-

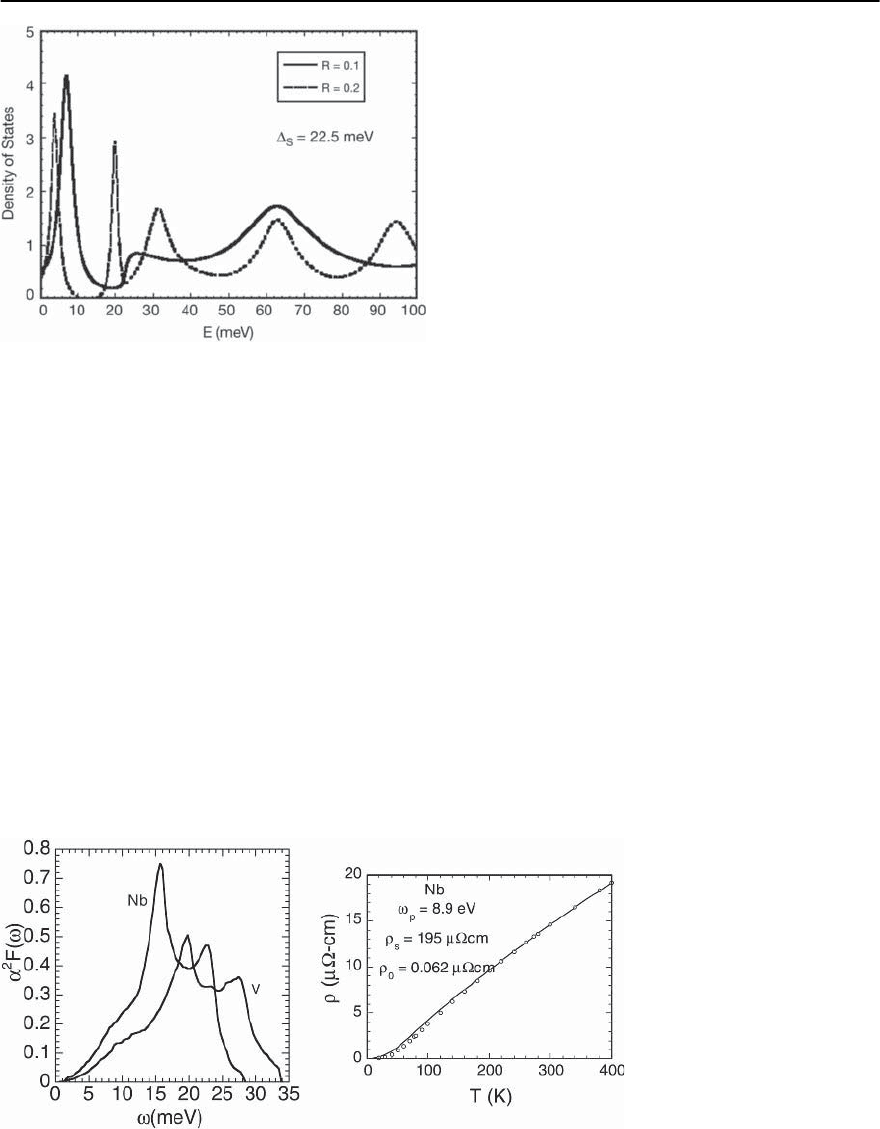
amples of these spectra using the PETS method are

shown in Fig. 15.16. These and other ˛

F(!)spectra

have been used successfully to determine the phonon

contributionto the temperature dependent electrical

resistivity above T

in several superconducting ele-

ments and compounds. An example of the fit of Nb

data is shown in the right panel of Fig. 15.16 taken

from the work of Tralshawala et al. [5]. The PETS

method has been used to examine alloys such as

NbZr as well as A-15 compounds such as Nb

Sn [1].

After the discovery that a thin Al overlayer could

provide a pinhole free oxide barrier on Nb, the prox-

imity effect method was extended to SIS junctions of

thetypeNb/Al/Al-oxide/Nbwhereitwasshownthat

excellent Josephson tunnel junctions could be ob-

tained.Further development of this method included

the patterning of arrays of such junctions which are

now the basis for all superconducting electronic de-

vices [38].

15.5 Tunneling in High-Temperature

Superconductors

Since the discovery of high temperature supercon-

ductivity in layered copper oxides by Bednorz and

M¨uller [39] in 1986 there has been a worldwide effort

to obtain tunnel junctions on these materials. Many

of the early efforts suffered from complications ow-

ing to the ceramic nature of cuprates and the fact

that the superconductivity exists only over a narrow

Fig. 15.16. Left: ˛

F(!)forNb

andV obtained from N/S prox-

imity bilayers using Al overlay-

ers. Right:thefittoNbresistiv-

ity using the electron–phonon

spectral function, from Tral-

shawala et al. [5]